破坏水库水温分层系统的能量效率估算:以金盆水库为例

孙 昕,叶丽丽,黄廷林,刘 伟 (西安建筑科技大学环境与市政工程学院,陕西 西安 710055)

破坏水库水温分层系统的能量效率估算:以金盆水库为例

孙 昕*,叶丽丽,黄廷林,刘 伟 (西安建筑科技大学环境与市政工程学院,陕西 西安 710055)

为指导高效节能的破坏水库水温分层技术及系统的选择,需建立统一的能量效率基准.根据质量守恒和热量守恒定律,求出分层水库水体完全混合后的水温,计算水库水体混合前后的重心;采用库容以及与水温相关的密度等数据,对水深方向各微小水层的势能进行积分得到水体总势能,混合后水体总势能的增加量即为破坏分层所需的最小理论能量,应用耗电量估算法得到破坏分层所产生的最小碳排量;破坏分层系统的能量效率为破坏分层的最小理论能量与实际输入能量之比.以西安金盆水库为例,采用数值模拟方法计算不同水位下的水库库容,应用该方法估算了水库不同季节破坏分层所需最小能量和扬水曝气破坏分层系统的能量效率.采用数值模拟方法计算不同水位下的水库库容,计算破坏分层所需最小能量.结果表明随水体垂向温度梯度的增加而增大,在6～10月期间相对较高,7月达到最大值2432.08kW·h;该水库扬水曝气破坏分层系统的能量效率约为4%;在水温分层开始阶段运行破坏分层系统可有效降低破坏分层所需的能耗,减少碳排放量.

分层水库；温度结构；破坏分层；能量效率

日益加重的资源型和水质型缺水,使水库逐渐成为我国多数城市的主要供水水源.在多数水深超过30m的水源水库中都会普遍出现温度分层现象,自上而下形成水温变幅较小的变温层、温度梯度较大的跃温层和水温恒定的等温层[1].跃温层阻碍上下水层的物质和能量交换,水体底部溶解氧会因各种生物和化学反应而消耗,当底部溶解氧浓度低于2mg/L时,底泥中的无机和有机污染物会大量释放形成内源污染[1-2],并由此引发水体富营养化等一系列水质问题[3-5].为保证和提高深水型湖泊水库的水质,破坏湖库水体温度分层是一种经济有效的水质改善方法[6-8].

和传统的饮用水处理工艺相比,破坏水体分层可以原位改善水源水质,并显著降低饮用水处理的综合成本[1].

理想的破坏分层技术应该效果好、能耗低、排碳少;但在计算破坏分层系统的能量需求方面存在较大的不确定性,在优选各种破坏分层技术时也面临能量效率的计算基准缺乏问题.实际湖泊水库的地形和水温结构非常复杂,计算破坏分层系统的能量输入很具有挑战性.目前,除了少数文献报道了试验规模的能量输入外[9],自然水体的能量输入还未见报道.理论上,破坏湖泊水库分层前后水体的温度结构发生改变,破坏分层后水体的总势能会相应增加,增加量即近似为破坏分层所需的最小能量,破坏分层系统实际的能量输入则取决于破坏分层系统的能量效率.

为优选高效节能减排的水库破坏分层技术和系统,最小化源水处理行业的能耗和碳排放量,需要合理确定破坏分层所需的能量,采用统一的破坏分层系统的能量效率.本文建立的估算破坏水库水温分层所需能量和破坏分层系统能量效率的计算理论,能够指导破坏分层系统能量供应的设计以及不同破坏分层系统能量效率的比较,对在源水处理行业减少碳排量有重要的理论意义和实际应用价值.

1 理论方法

1.1 稳定指数

Szyper[9]针对一个形状规则的小型池塘,将稳定系数S (g·cm/cm2)、重力加速度g (980cm/s2)以及池塘面积(cm2)相乘得到水体完全混合所需的能量(erg=10-7J),即将水体重心提高到温度完全相同的等温水体的理论高度.将分层水体沿着水深方向均匀分为n层,则稳定系数S为:

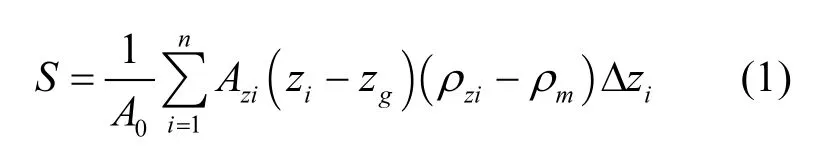
式中:zi为测量点深度,cm;Δzi为两测量点中点之间的距离,cm;A0表示池塘的表面积,cm2;Azi表示zi深度处池塘的面积,cm2);zg表示池塘水体完全混合后重心处的深度,cm,等于∑ (ziAziΔzi)/V;ρzi为zi深度处水体的密度,g/cm3);ρm为水体完全混合后的密度,g/cm3,等于∑ (ρziAziΔzi)/V;V为池塘的体积.

由于上述方法中的池塘水深较浅,面积较小,对池塘完全混合前后各处的温度和密度的测量也较为方便,但是并没有考虑破坏分层后水体的体积变化.换而言之,基于稳定系数的上述方法只适用于水深较浅、地形简单的分层水体.对于水深几十米甚至高达几百米的地形复杂的实际湖泊和水库而言,这种方法并不能用于计算破坏分层所需的能量.

1.2 势能

本文中破坏湖泊或水库水温分层所需的最小能量即是破坏分层后水体的势能增加量.

1.2.1 混合后的平均水温 根据湖泊或水库水体水温分布情况,将水体垂向每隔一定距离分为一层.对于第一层水体,层顶即为水面,层底位于第一、第二测量点的平均水深处;对于第二层水体,层顶为第一层水体的层底,层底位于第二、第三测量点的平均水深处;对于最后一层水体,层顶为上一层水体的层底,层底即为水体底部.每层垂向距离的中点被视为每层水体的重心.水体混合前,每层水体的温度为Ti1,密度为ρi1,运用湖库库容与水位的关系求得每层水体的体积Vi1,则等效重心高度为:

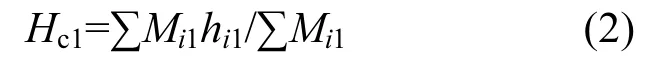
式中:Mi1为混合前每层水体的质量;hi1为水平面到每层水体重心的距离.

水体温度分层被破坏、完全混合后,假设破坏分层期间热量(Q)不损失,混合后的平均水温T2可由式(3)计算:

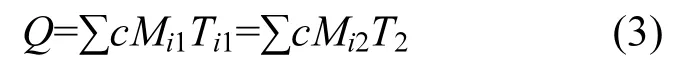
Mi2为混合后每层水体的质量,且∑Mi2=∑Mi1.

1.2.2 破坏分层前后水体的势能增加量 由以上可得混合后每层水体的密度ρi2以及混合后的总体积V2.由于混合前后水体密度发生变化,必然引起体积的变化,变化量△V=∑Vi1-V2.对于实际湖泊或水库,水体体积取决于水库的地形以及水深,实地测量湖泊或水库的水体体积的技术难度很大.混合后水深h2可由库容与水位的关系求得.引入变化系数δ=h2/h1,乘以混合前分层高度即得到混合后分层及每层重心高度hi2,则混合后水体等效重心高度为:

由于水库分层被破坏以后,水库水温降低,密度增加,从而导致水体分层时的重心高度比混合后的低,如图1所示.

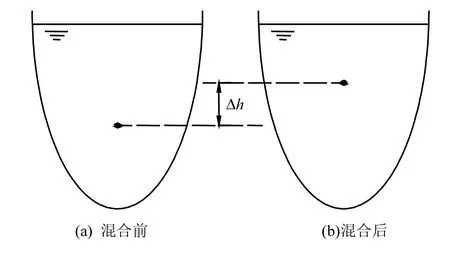
图1 水体混合前后重心的变化Fig.1 Variations of center of gravity of water before and after mixing

由于水体混合后重心上移,引起水体势能增加,增加量为:破坏分层所需的最小能量即为水体混合后势能的增加量△Ep.

1.2.3 破坏分层所需能量及碳排量 上述破坏分层前后的势能增加量是基于完全破坏分层的简化计算值,而更全面的能量估算需要考虑大气-水界面的热交换,包括长波辐射、短波辐射、水面蒸发和热对流.大气长波辐射、蒸发和传导均属于表面传热,表面传热一般影响深度不超过2m.太阳短波辐射则属于穿透传热,其影响深度可达数十米.

根据Hodges的水体热交换模型[10],水体表面总的热交换量(QS)为长波辐射量(QR)、表面短波辐射(QS)、水面蒸发量(QW)、水面显热对流量(Qh)之和.以金盆水库为例,根据表1所示该水库地区的气象资料[11],计算出水体表明传热量在3～8月为正值,水面温度处于缓慢的升温过程,尤其夏季升温剧烈;9～12月为负值,水面温度处于降温过程,冬季降温明显(图2).

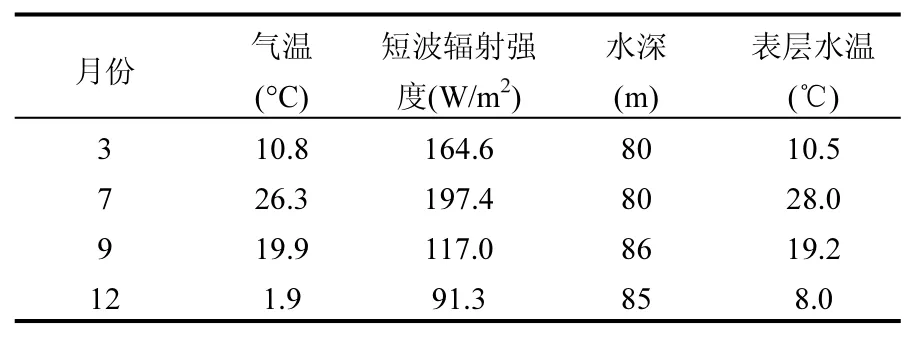
表1 2009年周至地区相关气象和水文资料(月均)Table 1 Meterological and hydrological data of Zhouzhi Region in 2009

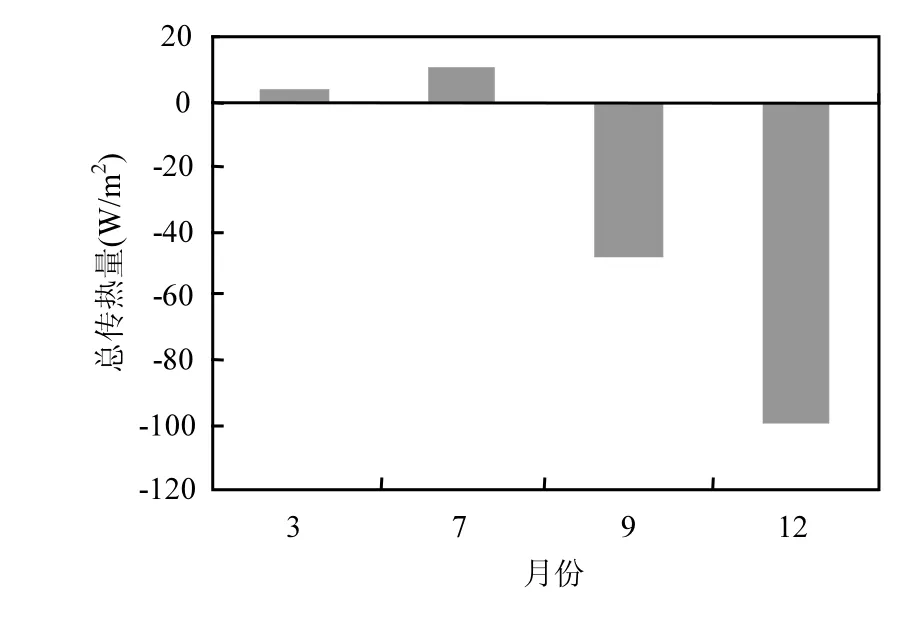
图2 不同月份表面总传热量Fig.2 Total surface heat transfered of various months

为安全起见,在计算水体混合后势能的增加量△Ep时,应利用破坏分层设备运行月份的表层水温最大日的垂向水温分布数据.式(5)所示最小能量除以破坏分层系统的能量利用率即得到破坏分层系统的实际能量输入(△E).

由于每发1度(kW·h)电所产生的温室气体折算成二氧化碳的量为8.448×10-4t,设为电力排放因子[12],用其乘以总耗电量即可得到破坏分层水库分层所产生的碳排量.

不同日期水库的水温分层结构以及水位不同,即水体混合前后的重心不同,导致破坏分层所需的最小能量亦不相同,故产生的碳排量也不尽相同.

此外,当水库水温分层被完全破坏以后,水库水体各处水温均一,但由于大气-水体热交换的客观存在,水面水温和气温会存在一定差异.在分层逐渐削弱的9～12月可停止运行破坏分层设备.而在分层逐渐加强的3～8月,仍需以较低功率运行破坏分层设备,以能维持上下层水体之间的弱循环,使水体处于持续的完全混合状态.即维持完全破坏分层状态所需能量及碳排放量因季节而异.

2 金盆水库案例分析

2.1 地形测量

金盆水库为西安市主要的饮用水水源,距离西安市约86km,供给西安市80%以上的水量,日平均供水量为76.0万m3,供水保证率95%.水库设计水位为594.0m,总库容为2.0亿m3,有效库容为1.77亿m3,主库区典型水深为80m,雨季水深可达90～105m.

为了计算不同水深下的水体体积,首次使用基于实时动态差分法(RTK)的全球定位系统以及测深仪来获取金盆水库准确详细的地形数据.水库主库区水面区域的水平坐标和水深分别用RTK系统(中海达V8Star)和测深仪(中海达HD-27T)来测量,便可得到库底区域三维坐标.为了确保测量的准确性,表2列出了设在主库区附近的3个控制点坐标.

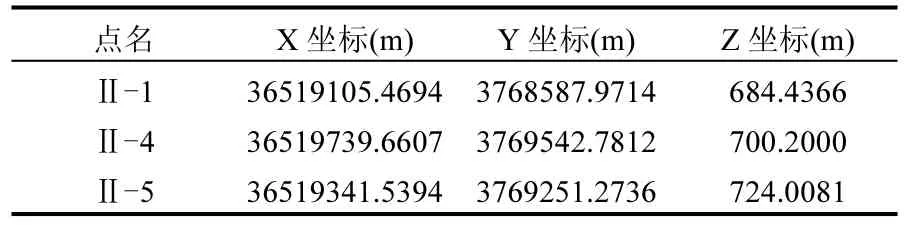
表2 控制点三维坐标Table 2 Three-dimensional coordinates of control points

中海达V8Star CORS RTK 系统是最新的一款具有GPRS、CDMA、UHF内置电台、URS集成数据中转站4种数据传输模式的多通道、多频率的先进GPS系统,它应用实时动态差分法(RTK)获取水库地形数据,由基准站与集成数据中转站(图3a)和移动站(图3b)构成.RTK系统的最大更新率为5次/s,测量极限为70km,平面精度±1cm,高程精度±2cm.中海达HD-27T测深仪由主机和换能器组成,发射频率为200kHz,测深极限为600m,测深精度±2cm.V8STAR系统的移动站和HD-27T测深仪放置于尺寸为4.2m×1.7m× 0.65m的双体电动船(图3b)上,该船具有水上测量作业平台,稳定性高,航速缓慢(航速5～8km/h).

图3 V8STAR RTK系统基准站(a)和移动站(b)实景照片Fig.3 Field photos of base station (a) and rover station (b) of V8STAR RTK system

按照25m×25m的水平测量网格,运用RTK精确测定了金盆水库库底详细的三维坐标.测得的金盆水库主库区地形见图4.

图4 金盆水库主库区地形Fig.4 Geometry near the main dam of Jinpen Reservoir

2.2 水库库容

利用RTK系统获得的金盆水库地形数据,采用Matisse构建了水库坝前的非结构三角形网格.运用Telemac-2D商业计算流体力学(CFD)软件[13],根据水库水位的月季均值,数值计算不同水位下的水库库容.根据不同水位下库容的数值计算值(图5),水库主库区库容从水位490m时的0m3逐渐增加到设计水位494m时的4.83×108m3.水库库容(y)可以表示成水位(χ)的函数,如图5所示,水位550m以下和以上的函数关系式分别为y=4139.6χ2-4.0×106χ+9.0×108(490m<χ<550m)和y=1260.8χ2-8.0×105χ+8.0×107(550m<χ<600m).每层水体的体积即为每层水体的高低水位对应的库容之差.

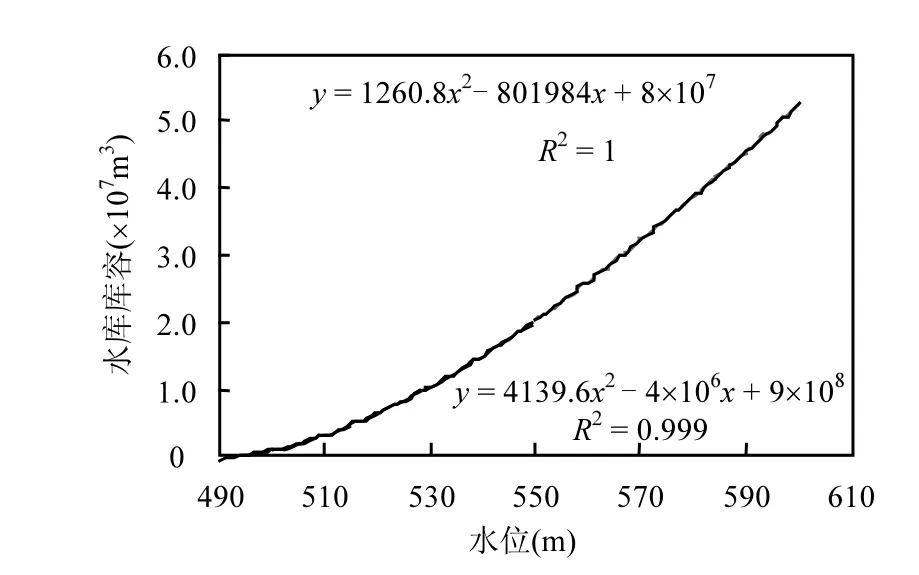
图5 金盆水库库容与水位的关系Fig.5 Relationship between the capacity and water level of Jinpen Reservoir

2.3 破坏分层所需能量

2.3.1 温度结构 采用Hydrolab DS5型多功能水质分析仪(美国HACH)对水库垂向水温进行年际监测,不同日期的水温剖面如图6所示[14].

图6 金盆水库水温结构Fig.6 Thermal structure of Jinpen Reservoir

根据王银珠和濮培民的研究结果[15],将垂向的温度梯度大于0.2℃/m的水层定义为跃温层.从图6可以看出,3月水库处于弱分层期,跃温层约位于水深3～8m处,跃温层内温差约为3℃.7月水库处于强分层期,跃温层约位于水深3～19m处,跃温层内温差约为20℃,水深2.5m内为上部变温层,水深19m以下为等温层.9月水库水温分层不断减弱,跃温层约下潜至水深30～70m处,跃温层内温差约为8℃,水深30m内为变温层.12月,冬季气温较低,上下层水体温差微小(约1.9℃),基本处于等温状态,不存在跃温层.该水库冬春季节为完全混合期,夏秋季节为水温分层期,尤其7～8月,水温分层最为强烈,跃温层最为稳定、厚度最大,水温结构的演变特性与平均水深87m的抚仙湖的情况大体类似[15].

2.3.2 破坏分层所需最小能量 根据图6所示

的金盆水库水温结构,由热量守恒式(3)计算出不同日期完全混合后的水温,如图7所示.冬春季节,混合后的等效平均水温在6℃左右,并在2月份达到最低值5.43℃;夏秋季节,混合的等效平均水温在14℃左右,并在8月份达到最高值14.85℃.此平均水温的计算结果符合理论预期.

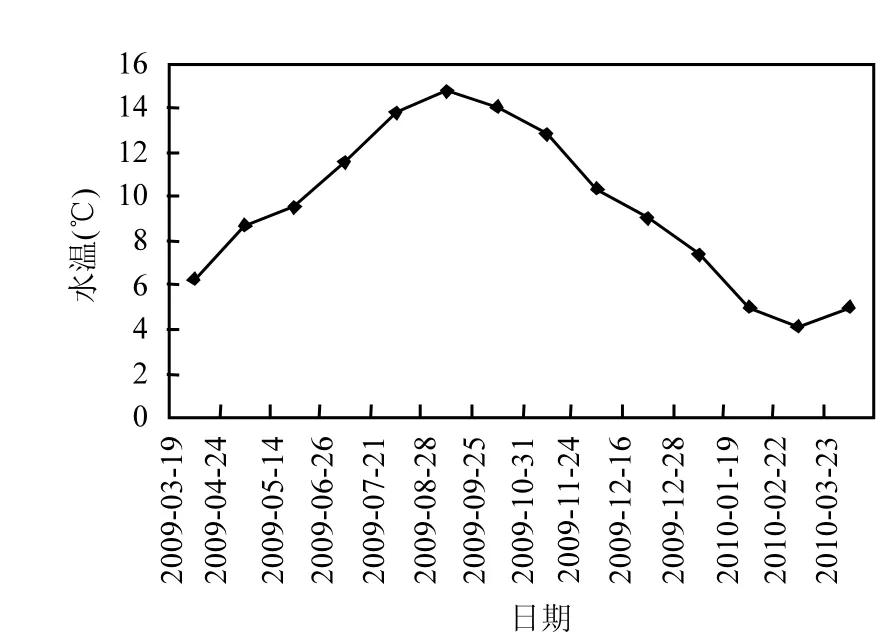
图7 不同日期完全混合后水温分布Fig.7 Average water temperatures of different dates after complete mixing

根据金盆水库不同的表层和底层水温差异及水深条件,计算得到不同日期完全混合前后水体的重心变化量以及破坏分层所需的最小动能,如图8所示.

可以看出,金盆水库水体从3月份开始分层,4～5月份逐渐形成水温分层,混合后的等效重心高度不超过1cm,破坏分层所需的最小能量从45.97kW·h逐渐增加到534.58kW·h.6～10月份水温分层稳定,混合后的等效重心高度逐渐增加,7月份到达峰值2.5cm,最小能量逐渐增加到7月份的2432.08kW·h,之后从此峰值逐渐减小到10月份的1088.36kW·h.11～12月份,水温分层逐渐减弱,混合后等效重心高度小于0.5cm,最小能量减小到41.38kW·h.次年1～2月份水温分层几乎完全消失,最小能量减小到3.82kW·h.

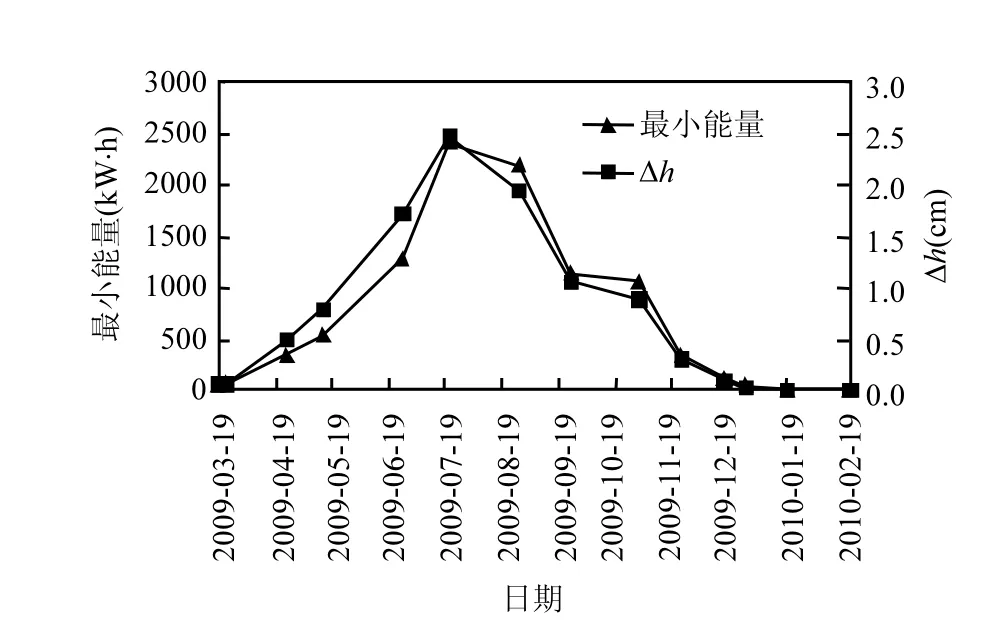
图8 不同日期的Δh以及最小动能Fig.8 Δh and minimum kinetic energy of different dates

现有破坏水库水温分层的传统技术主要有机械混合、空气混合、扬水曝气混合三大类,这些混合技术的核心是通过机械驱动或气提原理提升水库底部水体与表层水体混合.水库分层期间,上层水体温度较高、密度较小,而下层水体则相反.从破坏分层的角度而言,不论采取何种传统方式使上下层水体循环时,上层低密度水体被动下潜至下层高密度水体时会受到较大的浮阻力[16],这是水体混合时主要的阻力来源.此浮阻力与上下层水体密度差成正比,亦即水温分层越强(如夏季)、跃温层温度梯度越大,所受浮阻力越大[17];水深越大,所受浮阻力也越大.在水深较大、水面温度越大时,采用人工混合破坏分层时需克服的阻力越大、需要的最小能量越大.

等效重心高度主要取决于水体温度结构,水库分层结构变化,水体的重心也随之变化.对于分层水库,底部水体密度大,水库水体重心偏低;水温分层被完全破坏后,水库水体的重心会升高,升高的幅度取决于水域大小和原来的水温结构.金盆水库重心增加量小于2.5cm.由图8可见,3～4月份,混合前后重心变化量低于0.5cm;从5月份逐渐增加到7月份的2.5cm;然后逐渐降低,到12月份基本不变.对于跃温层深度为6m、上下界面处的温度分别为20℃和15℃的分层水库,水体混合前后重心增加量为0.6cm[18],与金盆水库的计算结果大致相符.

根据碳排放量与总耗电量的关系[12],可以计算不同月份破坏分层产生的最小碳排放量.仅破坏7月份水温分层所产生的碳排量就高达53.53t,而5t二氧化碳排放所占的空间约为2780m3,大于一个国际游泳比赛专用泳池的体积.中国工业和经济的高速发展,使得水处理行业产生的碳排量不容小觑.

2.3.3 破坏分层系统的能量效率 尽管分层破坏后水体重心高度仅增加数cm,但是破坏分层所需的实际能量输入一般都远大于理论的最小能量值,即破坏分层所产生的碳排放量也要远远大于其理论值.其中主要原因有两个:一是实际水库水体体积巨大,二是目前常用的曝气等破坏分层的技术方法能量效率普遍较低,通常低于10%[1],能量效率为破坏分层所需的最小能量与实际能量输入的比值.

根据西安金盆水库扬水曝气水质改善工程运行数据[19],主坝前1.1km范围库区内,呈梅花形布置安装8台扬水曝气器,各扬水曝气器间距250～300m.单台曝气器供气流量20～30m3/h,供气压力0.7～1.0MPa,气弹释放周期2～3min,提水量(1.2～1.3)×105m3/d.年运行电费1140480kW⋅h,破坏7月份水温分层约需20d,实际能量(△Ea)输入为63360kW⋅h,能量效率(η)约为4%.对于气泡羽流技术,Zic等[20]根据实验室结果,报道的能量效率约为3%;根据实际水库破坏分层装置的运行结果,Matsunashi等[21]报道的能量效率为4%～5%, Baines等[22]报道的能量效率约为8%.

上述实际破坏水温分层系统的能量效率的计算结果充分说明,只有改变传统的曝气混合技术思路,才能研发出真正高效的破坏湖泊水库水温分层技术,相应地减少碳排量.

3 结论

3.1 提出了分层水库水体完全混合前后的势能变化是破坏分层所需的最小能量的理论,破坏分层系统能量效率为所需最小能量与实际输入能量之比,建立了破坏分层所需最小能量及破坏分层系统能了效率的理论计算方法.

3.2 以金盆水库为例,估算了破坏水库分层所需最小能量的月季变化,该能量主要和水温分层水平成正比,在分层形成初期相对较低,分层稳定期相对较高,7月该能量达到最大值2432.08kW·h;估算了该水库扬水曝气破坏分层系统的能量效率约为4%,与国外其他系统的能量效率相近.

3.3 破坏分层系统应在分层形成初期运行,以降低能耗,减少碳排量;需突破传统曝气混合思路,研发高效率、低碳排放的破坏分层技术.

[1] 孙 昕,黄廷林.湖泊水库水体污染控制 [M]. 武汉:湖北科学技术出版社, 2013.

[2] 夏品华,林 陶,李存雄等.贵州高原红枫湖水库季节性分层的水环境质量响应 [J]. 中国环境科学, 2011,31(9):1477-1485.

[3] 姚玲爱,许振成,赵学敏,等.高州水库水华优势种铜绿微囊藻生长特性研究 [J]. 中国环境科学, 2013,33(S1):191-197.

[4] 黄廷林,杨凤英,柴蓓蓓,等.水源水库污染底泥不同修复方法脱氮效果对比实验研究 [J]. 中国环境科学, 2012,32(11): 2032-2038.

[5] Maria C P, Jose M A, et al. Effects of warm water inflows on the dispersion of pollutants in small reservoirs [J]. Journal of Environmental Management, 2006,81:210-222.

[6] Lawson R, Anderson M A. Stratification and mixing in lake Elsinore, California: An assessment of axial flow pumps for improving water quality in a shallow eutrophic lake [J]. Water Research, 2007,41(19):4457-4467.

[7] Hill D F, Vergara A M, Parra E J. Destratification by mechanical mixers: Mixing efficiency and flow scaling [J]. Journal of Hydraulic Engineering, 2008,134(12):1772-1777.

[8] Yum K, Kim S H, Park H. Effects of plume spacing and flowrate on destratification efficiency of air diffusers [J]. Water Research, 2008,42(13):3249-3262.

[9] Szyper J P. Comparison of three mixing devices in earthen culture ponds of four different surface areas [J]. Aquacultural Engineering, 1996,15(5):381-396.

[10] Hodges B R. Heat budget and thermodynamics at a free surface [R]. Centre for Water Research, The University of Western Australia, 1999.

[11] 吴林荣,江志红,鲁渊平,等.陕西太阳总辐射的计算及分布特征[J]. 气象科学, 2009,29(2):187-191.

[12] 王曦溪,李振山.1998—2008年我国废水污水处理的碳排量估算 [J]. 环境科学学报, 2012,32(7):1764-1776.

[13] Sun X, Shiono K, Rameshwaran P, Chandler J H. Modelling vegetation effects in irregular meandering river [J]. Journal of Hydraulic Research, 2010,48(6):775-783.

[14] 邱二生.黑河水库水质及藻类监测和水体分层研究 [D]. 西安:西安建筑科技大学, 2010.

[15] 王银珠,濮培民.抚仙湖水温跃层的初步研究 [J]. 海洋湖沼通报, 1982,4(4):1-9.

[16] Fischer H B, List J E. Koh C R, et al. Mixing in Inland and Coastal Waters. London: Academic Press, 1979.

[17] 孙 昕,叶丽丽,赵伟丽等.分层水库温度梯度对扬水曝气原位控藻效果的影响 [J]. 中国环境科学, 2014,34(2):352-358.

[18] Kirke B, Gezawy A E L. Design and model tests for an efficient mechanical circulator/aerator for lakes and reservoirs [J]. Water Research, 1997,31(6):1283-1290.

[19] 马 越,黄廷林,丛海兵,等.扬水曝气技术在河道型深水水库水质原位修复中的应用 [J]. 给水排水, 2012,38(4):7-13.

[20] Zic, K, Stefan, H G., and Ellis C. Laboratory study of water destratification by a bubble plume [J]. J. Hydraul. Res., 1992, 30(1):7–27.

[21] Matsunashi G, Miyagawa Y. A field study on the characteristics of air bubble plume in a reservoir [J]. J. Hydrosci. Hydraul. Engng. Proc. JSCE., 1990,9:65–78.

[22] Baines W D, and Leitch, A M Destruction of stratification by bubble plume [J]. J. Hydraul. Eng., 1992,118(4):559–577.

Estimation of energy efficiency of a destratification system for reservoirs: a case study of Jinpen Reservoir.

SUN Xin*, YE Li-li, HUANG Ting-lin, LIU Wei (School of Environmental and Municipal Engineering, Xi’an University of Architecture and Technology, Xi’an 710055, China). China Environmental Science, 2014,34(11)：2781～2787

In order guide the selection of effective and energy-saving destratification technologies for reservoirs, an uniform criteria of energy efficiency should be developed. The average water temperature after complete mixing can be calculated based on the conservation laws of mass and heat, the reservoir’s gravity centres before and after mixing were calculated.The total potential energy (PE) was determined by integrating the PE in each thin sub-layer over the water depth with data of water volume and density depending on the water temperature. The difference of total potential energy before and after mixing is the minimum energy input required for destratification. The minimum carbon emission from destratification was then calculated based on conversion ratio of the energy consumption to carbon emission. The energy efficiency of a destratification system was the ratio of the minimum required energy input to the actual energy input for destratification. Taking Jinpen Reservoir in Xi’an as a study case, water volumes under different water levels of the reservoir were numerically calculated using the geometry data, this new method was applied to estimate the energy input required for destratification and energy efficiency of destratification system. Minimum energy required for destratification of different months were both calculated using the geometry data. The results showed that minimum energy increase with the temperature gradient, was relatively high during the period from June to October, and reached a peak of 2432.08kW·h in July. The energy efficiency of the water-lifting aeration system was about 4%. It would be efficient at reducing the energy required for destratification and saving carbon emission by running the destratification system at the initial stratification period.

stratified reservoirs；thermal structure；destratification；energy efficiency

X524/TU991

A

1000-6923(2014)11-2781-07

孙 昕(1971-),男,安徽桐城人,副教授,博士,主要从事水质污染控制与模拟研究.发表论文30余篇.

2014-01-13

国家自然科学基金资助项目(51178379,51278404);国家科技支撑项目(2012BAC04B02);教育部高等学校博士点专项科研基金(20106120120012);西安建筑科技大学人才科技基金(RC1130).

* 责任作者, 副教授, xinsunn@gmail.com