变曲率曲面周铣铣削力建模与分析*

郝洪艳 汤文成 王保升

(①东南大学机械工程学院，江苏 南京211189;②南京工程学院材料学院，江苏 南京211167)

在模具、电子、航天航空等产品中存在大量的变曲率曲面，使铣削稳定性预测、工艺系统变形分析和铣削参数优化更加复杂。解决这些问题需要建立精确的铣削力模型，揭示曲率对铣削力的影响规律。一直以来，对铣削力的研究多集中于直线铣削和圆弧铣削，在变曲率铣削方面的研究相对较少。Zhang 建立了圆弧铣削的铣削力模型，通过改变圆弧半径分析了曲率对等效进给量、切入角、切出角以及铣削力的影响［1］。Rao针对变曲率曲面周铣建立了铣削力解析模型，分析了曲率对平均铣削力的影响［2］，但对最大曲率处的铣削力峰值和谷值变化未做深入研究。浦金鹏分析了曲率对等效每齿进给量的影响，进而定性分析了曲率对铣削力的影响［3］。王小纯利用试验法研究了小直径铣刀侧铣时刀位路径曲率对铣削力的影响，建立小直径铣刀铣削淬硬钢的切削力与刀位路径的灰色模型［4］。以上研究所提出的铣削力模型均未考虑刀具偏心跳动的影响。Desai 提出了包含刀具偏心跳动的铣削力模型，给出切削厚度的隐式算法，需要耗费大量计算时间［5］。Yang 提出基于NC 代码的刀位点确定方法，在将微段曲线简化为圆弧的基础上给出了未变形切屑厚度的显式计算公式［6］。

本文基于直线插补的理念确定刀具位置，在考虑刀具偏心跳动的情况下，通过坐标变换推导未变形切屑厚度的新算法，给出包含工件边界的切入角与切出角计算方法。最后通过试验验证模型的有效性，并进一步分析曲率对切入角、切出角、未变形切屑厚度、进给方向力和法向力的影响。

1 铣削力建模

1.1 铣削力基本模型

变曲率曲面周铣如图1 所示，oxy 为固定坐标系，osxsys为随动坐标系，osxs、osys分别为曲线在该点的切线方向和法线方向。(xt(u)，yt(u))、(xw(u)，yw(u))、(x(u)，y(u))分别为刀具中心轨迹曲线、加工前轮廓曲线和加工后轮廓曲线。A、B 表示刀具中心，C、D 表示对应的刀齿切入点。

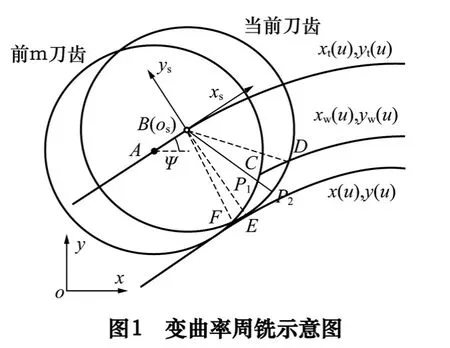
沿刀具轴向将刀齿进行离散化，作用在第i 个刀齿第j 个微元上的切向力dFti，j(u)和径向力dFri，j(u)为

式中:dz 为轴向宽度;hi，j(u)为瞬时未变形切屑厚度;u 为曲线参数;Kt(hi，j(u))和Kr(hi，j(u))分别表示切向和径向切削力系数，与未变形切屑厚度呈幂函数关系［7］。

将微元切削力转化为osxs与osys方向分量，并对所有微元切削力求和，则总铣削力为

式中:φsi，j(u)为微元在随动坐标系的位置角。

将铣削力变换到固定坐标系中，铣削力在ox 与oy向的分量为

式中:θ(u)为进给方向角。

1.2 刀具位置确定

与直线铣削和圆周铣削不同，变曲率铣削中刀具位于不同位置时，曲率不同会造成未变形切屑厚度、切入角与切出角等工艺参数的变化。以加工后工件轮廓曲线为基准，三条曲线对应同一参数时的坐标关系为

式中:ae为径向切深;R 为刀具半径;x'(u)、y'(u)表示参数化曲线的微分。

利用直线插补方法将刀具中心轨迹曲线离散为若干微段，以两点间的直线逼近曲线，相邻点距之和作为刀位轨迹长度。当刀位对应参数uk时，进给方向角θ(uk)、加工时间T(uk)及刀具位置角φs(uk)为

式中:vf为进给速度;n 为主轴转速;Lt(ug，ug+1)为相邻点距。

1.3 未变形切屑厚度的新算式

不考虑刀具偏心跳动时，未变形切屑厚度可以通过等效进给量、微元在随动坐标系中的位置角进行计算［2］。但在刀具偏心跳动和曲率变化的共同作用下，未变形切屑厚度的计算将变得比较复杂。

如图1 所示，P2为刀齿i 瞬时位置，P1为BP2与刀齿i-m 切削路径的交点。瞬时未变形切屑厚度表示为

式中:Ri，j为微元实际切削半径;ρ 为刀具偏心量;λ 为偏心方向角;LBP1为BP1长度;Nf为刀齿数;β 为刀具螺旋角;zi，j为微元轴向高度。

为简化计算，利用坐标平移变换将B 移至原点，再利用旋转变换将AB 旋转至x 轴。坐标变换后，刀齿i-m 的切削路径方程及直线BP2的方程为

式中:LAB为AB 长度;K =ctan(φs(ub)-θ(ub)+ψ)，ψ=arctan((yt(ub)-yt(ua))/(xt(ub)-xt(ua)))。

解方程(8)得点P1的坐标，并计算LBP1为

式中:γ=φs(ub)-θ(ub)+ψ。

当m 取不同值时，依式(6)、式(7)、式(9)计算出所有可能的未变形切屑厚度，则瞬时未变形切屑厚度为

1.4 切入角与切出角计算

由于刀具偏心跳动的存在，刀齿的切出点可能是该刀齿与前一刀齿轨迹的交点，也可能是与前m 刀齿的交点，需计算当前刀齿与其前Nf个刀齿所有的交点，求解相应的切出角度，取其最小值［5］。因此，在刀具偏心跳动的影响下，切入角与切出角为

式中:φi，j，st(ub)与φi，j，ex(ub)为 切 入 角 与 切 出 角;φ(i，i-m)，j，ex(ub)为当前刀齿与前m 刀齿的交点对应的切出角;DF 为两点长度。

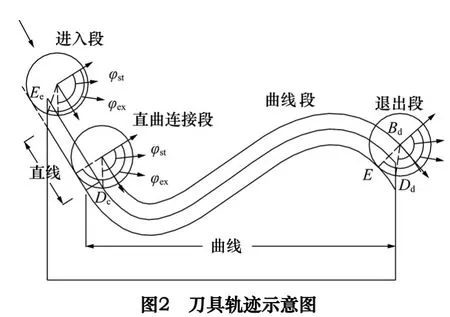
如图2 所示，在刀具进入阶段和退出阶段应分别考虑工件边界对切出角和切入角的影响，可以通过工件边界和刀齿轨迹计算出交点(图中Ee、Dd点)，从而得出进入阶段的切出角和退出阶段的切入角。

在直线与曲线连接阶段，切入与切出角仍可以依据式(11)、式(12)计算。

2 试验验证

试验在DMC 70V hi-dyn 高速加工中心进行。刀具采用Sandvik 1P240 - 1000 - XA1630，4 齿，直径10 mm，螺旋角35°。干切削，顺铣。工件材料为Al6061 -T6，测力仪为Kistler 9257B。

试验1:主轴转速3000 r/min，径向切深3 mm，轴向切深5 mm，进给速度480 mm/min，直线铣削，用于辨识切削力系数与刀具偏心跳动参数。

试验2:主轴转速3000 r/min，径向切深3 mm，轴向切深2 mm，进给速度360 mm/min，变曲率铣削，用于验证铣削力模型的有效性。工件目标轮廓如图2 所示。曲线段为三次贝塞尔曲线，方程为

利用试验1 的实测铣削力和文献［7］提出的方法辨识切削力系数及刀具偏心跳动参数，结果为

图3 是试验2 的预测铣削力与实测铣削力(ox 方向)，对比发现，二者变化趋势和幅值均具有良好的一致性，说明建立的铣削力模型是有效的，能够精确预测瞬时铣削力。

3 曲率对铣削力的影响分析

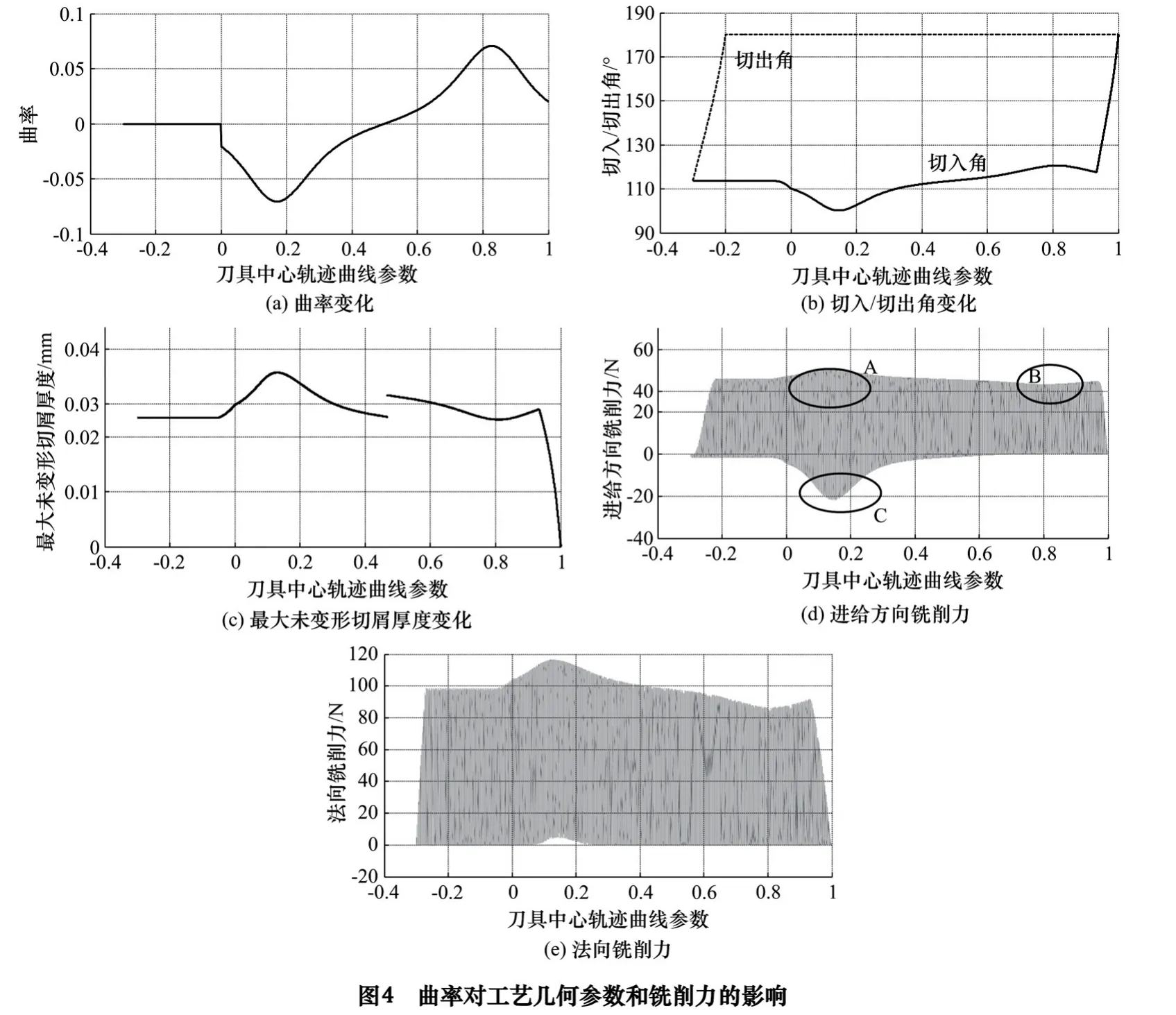
为便于分析刀具中心轨迹曲线的曲率变化对工艺几何参数和铣削力的影响，忽略刀具偏心跳动，以刀具中心轨迹曲线的参数(表示刀具中心位置)作为横坐标，对试验2 加工过程中的切入角、切出角、最大未变形切屑厚度、进给方向铣削力和法向铣削力进行仿真，结果如图4 所示。由仿真结果可得出以下结论:

(1)曲率对切入角、最大未变形切屑厚度、铣削力均具有明显的影响，且凹曲面铣削的影响均较凸曲面铣削更加显著。

(2)切入角、最大未变形切屑厚度的极值点对应的刀具中心轨迹曲线参数均小于最大曲率对应的刀具中心轨迹曲线参数，相对于曲率具有一定的“超前”，这是由刀具半径引起的，刀具半径越大，超前越显著。

(3)切出角受刀具中心轨迹曲线曲率的影响很小，近似为π;凹曲面铣削的切入角小于直线铣削时的切入角，且随刀具中心轨迹曲线曲率增大而减小。因此，凹曲面铣削的切角区间(切出角与切入角的差值，表示刀-屑切触范围大小)随曲率增大而增大;凸曲面铣削的切入角大于直线铣削时的切入角，且随曲率增大而增大，切角区间随曲率增大而减小。

(4)凹曲面铣削引起最大未变形切屑厚度增大，且随曲率增大而增大;凸曲面铣削时结论完全相反。

(5)凹曲面铣削时，进给方向铣削力和法向铣削力的峰值均随曲率增大而增大，凸曲面铣削时二者峰值随曲率增大而减小。由于铣削力的幅值主要受未变形切屑厚度影响，峰值极值点(图4d 中“A”、“B”区)与最大未变形切屑厚度的极值点发生在同一位置。法向铣削力峰值比进给方向铣削力峰值受曲率影响更加显著。

(6)进给方向铣削力和法向铣削力的谷值(图中“C”区)在凹曲面最大曲率附近发生明显变化，进给方向铣削力比法向铣削力变化更加显著，这主要由切入角变化引起，其极值点与最小切入角发生在同一位置。如图5 所示，在径向切深较小时，如果始终保持单齿铣削，即使曲率变化引起切角区间增大，铣削力谷值也不变化。只有出现多齿同时参与铣削，铣削力谷值才会出现变化。这一点对铣削参数优化和稳定性预测具有重要意义。

刀具偏心跳动对铣削力的影响规律与直线铣削时类似，本文不再赘述。

4 结语

变曲率曲面铣削中，当曲率变化较大时极有可能造成铣削力的超值突变，引起切削颤振，从而影响产品加工质量和加工效率，降低刀具寿命。本文基于直线插补给出了刀具位置角、进给方向角及加工时间的确定方法;采用坐标变换法推导出包含刀具偏心跳动的未变形切屑厚度新算式，提出包含工件边界的切入角与切出角计算方法，从而构建出变曲率铣削全过程的铣削力模型。利用本文提出的瞬时铣削力模型以及辨识出的瞬时切削力系数对铣削力进行预测，预测结果与试验结果具有良好的一致性，证明了该方法的有效性，并进一步分析揭示了曲率对铣削力的影响规律，为变曲率铣削稳定性研究提供了理论基础。

［1］L Zhang，L Zheng，Z H Zhang，et al. On cutting forces in peripheral milling of curved surfaces［J］. Proceedings of the Institution of Mechanical Engineers，Part B:Journal of Engineering Manufacture，2002，216(10):1385 -1398.

［2］V S Rao，P V M Rao. Effect of workpiece curvature on cutting forces and surface error in peripheral milling［J］.Proceedings of the Institution of Mechanical Engineers，Part B:Journal of Engineering Manufacture，2006，220(9):1399 -1407.

［3］浦金鹏，庄海军.基于曲率的圆周铣削铣削力建模［J］.机械工程与自动化，2009(4):120 -122.

［4］王小纯，胡映宁，苏家强.小直径铣刀铣削力与刀位路径曲率关系的研究［J］.机械设计与制造，2008(10):205 -207.

［5］K A Desai，P K Agarwal，P V M Rao. Process geometry modeling with cutter runout for milling of curved surface［J］. International Journal of Machine Tools and Manufacture，2009，49(12 -13):1015 -1028.

［6］Y Yang，W H Zhang，M Wan. Effect of cutter runout on process geometry and force in peripheral milling of curved surfaces with variable curvature［J］. International Journal of Machine Tools and Manufacture，2011，54(5):420 -427.

［7］王保升.瞬时铣削力模型参数辨识及其试验研究［D］.镇江:江苏大学，2011.