决策树模型在水环境监测网络中选取代表性样点的应用

薛冬梅，王中良

1．天津师范大学，天津市水资源与水环境重点实验室，天津 300387

2．比利时根特大学同位素生物科学实验室(ISOFYS)，Ghent B-9000

3．中国科学院地球化学研究所，环境地球化学国家重点实验室，贵州 贵阳 550002

水体中硝酸盐的污染在全球范围内日益严重。各国亦建立相关水体监测网络对水质进行长期监测，但随之而来的是大量监测数据的累积，给后续的科研工作带来不便。尤其是在庞大的监测网络中如何选取有代表性样点的研究已成为急需解决的问题之一。

科学的统计方法对于庞大的数据处理很有意义。多元统计方法(Multivariatestatistical methods)能够区分众多变量之间的复杂关系，对于源类识别问题很有意义［1-3］。Alley［2］对多元统计方法进行了较为详细的综述，该法包括聚类分析(cluster analysis)、主成分分析(PCA)、判别分析(discriminant analysis)、决策树模型(decision tree)和因子分析(factor analysis)等。对于源类的分类问题，我们可以应用判别分析和决策树模型［4］。判别分析是多元回归以寻找最佳线性方程组来分离样本，但是此种方法很难进行合理解释。决策树模型的基本理论是根据一个已知分类的数据集以自上而下的递归方式构造决策树，并以此样本为基础进行归纳学习，而其表现形式就是一个类似于流程图的树形结构。决策树模型分类准确性较高、计算过程简单，输出结果具有图形化易理解等优点［5-7］。国内也有一些学者应用决策树模型研究如何评价耕地［8］、分类海岸带［9］、分类湿地［10-11］以及探讨黄河干流缺水［12］问题等。但目前还没有应用这类模型对于较大水体监测网络所收集的时间序列数据进行信息抽取挖掘的相关研究。

该研究以比利时弗拉芒地区的水环境监测网络为例，利用决策树模型分析评估原有监测点位的污染源专家分类和模型输出的可匹配率，为进一步选取代表性样点进行污染源判断的深入研究提供理论依据。

1 决策树模型的建立

1.1 采样点概况

专家从环境监测网络选取了47个采样点(图1)，并且根据硝酸盐来源划分为5类：温室大棚区(G，11个点位)、农作物区(A，7个点位)、有地下水补给的农作物区(AGC，15个点位)、居民区(H，8个点位)以及农作物和园艺混合区(AH，6个点位)。

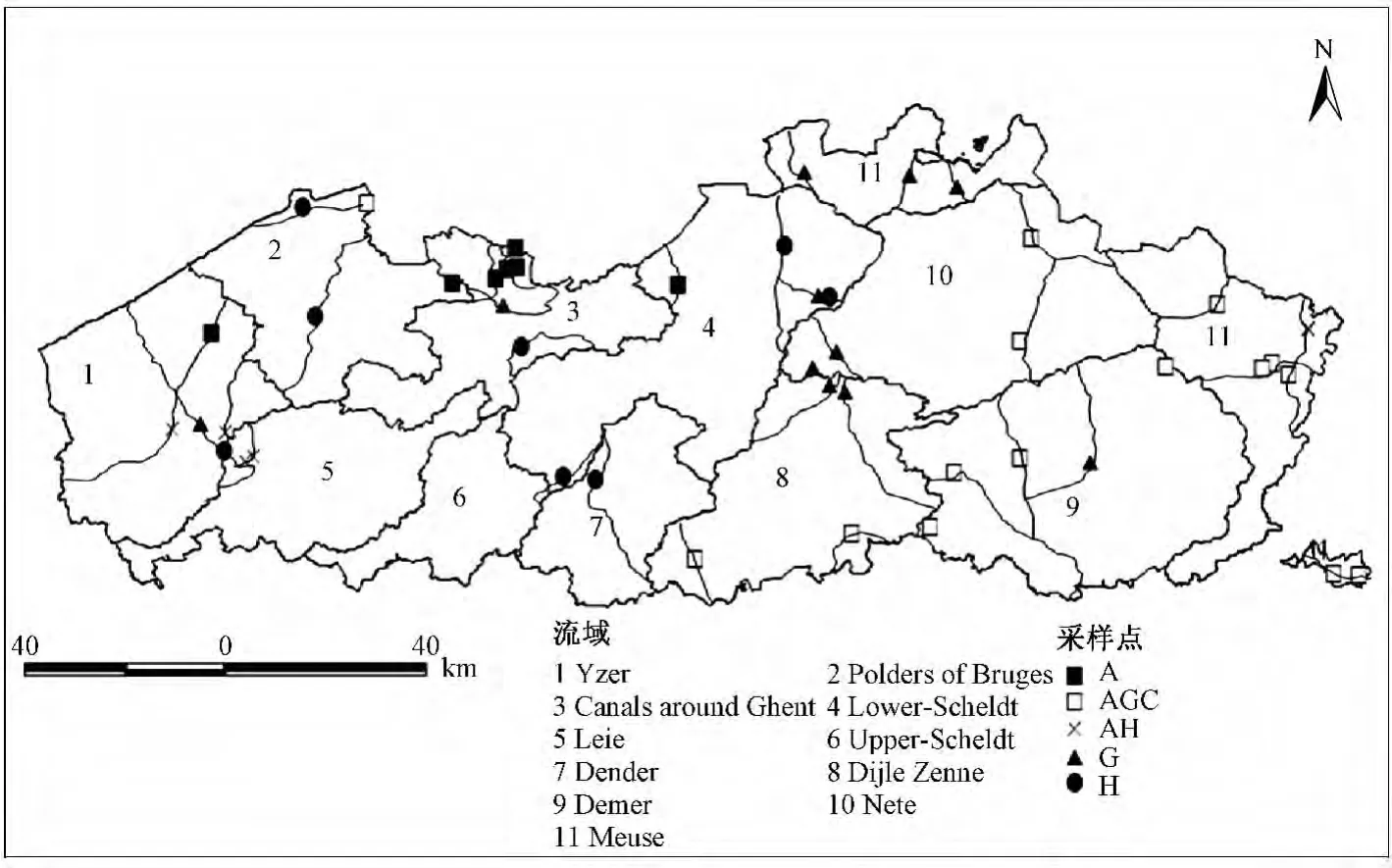
图1 地表水采样点的分布

1.2 数据集合

根据采样点在监测网络中的编码、采样时间，监测的地表水水体的10个物理化学参数(水温T，EC20，pH，DO，O2，Cl－，NH4+-N，NO2－，NO3－、PO)以及硝酸盐来源分类等指标创建了数据集合，实例总数为3 928。其中，数据集合中缺失的数据根据多重插补(Multiple Imputation)法进行插补。

分类AH以及G中的地表水站点在2002—2009年都具有较高的平均硝酸盐浓度范围，质量浓度分别为13.5～29.8 mg/L和6.9～44.4 mg/L;分类A以及AGC中的地表水站点的NO3－平均浓度次之，质量浓度分别为2～14 mg/L和1～22.4 mg/L;而分类H则为最低，NO3－平均质量浓度为0.4～3.6 mg/L(以N计)变化。

1.3 决策树模型

决策树模型的基本算法是贪心算法，其生成则是自上而下的递归过程通过不断将样本分割成子集来构造决策树。算法的核心问题就是属性选择和剪枝策略。采用C4.5算法来建立决策树模型［13］。C4.5对属性的选择基于信息理论(information theory)［14］，通过计算信息增益来确定节点的分裂属性，每个节点均选择具有最大信息增益的属性。这样能够使得样本在依据该属性进行分类时所需要的信息最小，可以有效减少分类所需的分裂次数。假设一个集合M，具有s个类别，其中个类在M中出现的比例为p(ci)，那么M的信息熵为

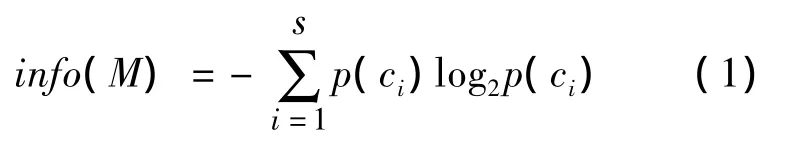
选择属性X(在本研究中是指水的物理化学参数)分裂后的信息增益可表达为

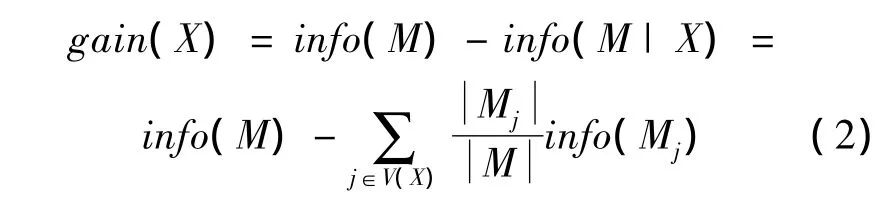
式中info(M|X)代表X的信息熵，V(X)代表属性X的可能值的数量，Mj代表集合M的子集中属性X的可能值的数量为j。最优属性则是信息增益gain(X)的最大值。

C4.5对决策树的剪枝是自下而上，从树最底层的节点，将符合修剪规则的剪掉，直到没有节点满足修剪规则为止。决策树建立后，根据10次交叉检验法进行准确性评估。

2 结果与讨论

2.1 模型输出与专家分类对比

利用47个地表水样点的10个物理化学参数数据建立了决策树模型，共有247个节点，树形规模较大。实例数量为3 928个，其中3 142个实例与专家知识的分类情况一致，剩余的786个实例则被分为不同的类别。所以，此决策树模型的输出与专家分类的匹配率为80%。决策树模型中每一硝酸盐源类实例的分类情况见图2。

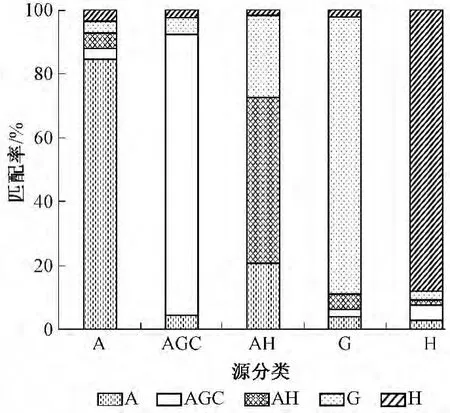
图2 决策树模型中每一硝酸盐源类实例的分类情况

从图2可见，分类A、AGC、G和H具有较高的匹配率(大于80%)，表明使用建模的物理化学参数数据具有较高的可重构性。分类AH则具有较低的匹配率(50%)，表明了这一类样点的物理化学参数数据具有较低的可重构性，但是引起这一现象的原因目前不详，需要结合后续的氮氧同位素方法进行深入研究。此外，每一硝酸盐源的模型输出与专家分类的匹配率都不是100%，说明部分实例与专家分类不相同。所以，了解决策树模型中每一类实例的分类情况是比较有意义的。

从图2中可以看出分类A、AGC、G和H具有较高的匹配率(大于80%)，因而这些分类中相应的实例被划分为其他分类的百分比则相对较低。相反地，分类AH因具有较低的匹配率而导致其相当部分实例(大于40%)被决策树模型重新分到A以及G这2个类别中。其原因可能是分类AH本身就是农作物和园艺混合区，此类中地表水样点所构成实例不排除具有其他类别实例的特征。

另外，47个采样点的平均决策树模型的输出与专家分类的匹配率为43% ～95%，有近3/4的样点大于80%。研究中还发现，分类AH中的采样点均显示了较低的数值，平均匹配率为43% ～60%。此类中的采样点数据重构性较差，需选择另外一种相对独立的方法进行分析研究，进而对采样点分类提供更合理的证据，并非只是单单从不同土地利用类型和专家知识而进行的分类检索。

2.2 依据决策树模型选择代表性样点

如前所述，决策树模型所评估的47个采样点中，部分样点数据重构性较差导致决策树模型的输出与专家分类的匹配率较低，需要其它方法进行校正。氮氧同位素方法已经广泛应用于对硝酸盐污染源判断以及硝酸盐迁移转化过程的研究。所以，在47个样点中选择了30个具有代表性的样点作为后续研究。另将30个优化后点位的数据集再次带入模型中，该决策树模型的输出与专家分类的匹配率达到84%，优于前47个点位的模型输出。然而分类AH中的采样点仍显示较低的匹配率(48% ～63%)。根据此决策树模型，缩减了工作量，选择的样点更具有代表性。其目的是通过后续方法更准确地对选择的样点进行分类，建立输出结果更为精确的决策树模型进而对监测网络中其它未知源的样点进行硝酸盐来源的预测。

3 结论

建立的决策树模型成功地从47个采样点的物理化学数据所组成的数据集中挖掘了未知的、有价值的信息。此决策树模型评估了约有80%的样点分类与专家知识分类相吻合，然而部分样点则显示了较低的匹配率，数据的可重构性较低。决策树模型的输出结果为选择有代表性样点进行后续研究提供了可靠的数据保证。

［1］Hem J A．Study and interpretation of natural water［M］．Water Supply Paper 2254．Reston，VA：United States Geol．Survey，1985．

［2］Alley W M．Regional ground-water quality［M］．Van Nostrand Rheinhold．New York：Wiley，1993．

［3］Spruill T B，Showers W J，Howe S S．Application of classification-tree methods to identify nitrate sources in ground water［J］．J Environ Qual，2002，31：1 538-1 549．

［4］Wilkinson L．Classification and regression trees［M］．Chicago：SPSS Inc，2000．

［5］Breiman L J，Friedman J H，Olshen R A et al．Classification and regression trees［M］．New York：Chapman and Hall/CRC，1984．

［6］Han J W，Kamber M．Data mining：Concepts and techniques［M］．San Francisco：Morgan Kaufmann Publisher，2001．

［7］StatSoft． Electronic statistics textbook ［EB/OL］．(2001)［2013-10-24］http：∥www．statsoft．com/．

［8］田剑，胡月明，刘建敏，等．聚类支持下决策树模型在耕地评价中的应用［J］．农业工程学报，2007，23(12)：58-62．

［9］何厚军，王文，刘学工．基于决策树模型的海岸带分类方法研究［J］．地理与地理信息科学，2008，24(5)：25-28．

［10］李慧，余明．基于决策树模型的湿地信息挖掘与结果分析［J］．地球信息科学，2007，9(2)：60-64．

［11］黄颖，周云轩，吴稳，等．基于决策树模型的上海城市湿地遥感提取与分类［J］．吉林大学学报：地球科学版，2009，39(6)：1156-1162．

［12］吴新，邓晓青．黄河干流缺水决策树模型研究［J］．人民黄河，2007，29(6)：25-27．

［13］Quinlan J R．C4.5：Programs for Machine Learning［M］． San Mateo， CA：Morgan Kaufmann Publishers，1993．

［14］Shannon C．A mathematical theory of communication［J］．The Bell Systems Technical Journal，1948，27：379-423．