地震条件下不同类型边坡的稳定性研究①

贺小黑王思敬

1. 中化地质矿山总局化工地质调查总院，北京 100013；

2. 中国科学院 地质与地球物理研究所，北京 100029；

3. 中国科学院工程地质力学重点实验室，北京 100029

应用地质

地震条件下不同类型边坡的稳定性研究①

贺小黑1王思敬2，3

1. 中化地质矿山总局化工地质调查总院，北京 100013；

2. 中国科学院 地质与地球物理研究所，北京 100029；

3. 中国科学院工程地质力学重点实验室，北京 100029

用sarma法计算了不同坡高、不同坡角、不同岩体和结构面力学参数的边坡在不同水平地震加速度系数下对应的安全系数，建立了一套能方便快捷地查询边坡安全系数的系统，为各种类型边坡的稳定性评价提供了依据。此外，还分析了坡高、坡角、地震加速度系数、岩体和结构面力学参数对地震边坡安全系数的影响。通过对比查询系统得到的安全系数与其他已有的地震边坡稳定性评价方法得到的安全系数的差异，得出用这种新安全系数查询方法得到的安全系数与其他安全系数计算方法得出的安全系数相差不大。通过将这种新的地震边坡稳定性评价方法应用到几个实际边坡中，所得到的评价结果与滑坡的实际发生情况一致。

地震边坡；安全系数；岩体和结构面力学参数；水平地震加速度系数；sarma法

0 引言

地震诱发的滑坡和崩塌是常见的地质灾害,我国是一个多山多地震的国家,因地震而导致的滑坡灾害十分严重【1】。汶川地震以来，人们对这种灾害投入了更多的关注。地震条件下边坡的稳定性研究是边坡研究中的重要内容，安全系数是反映边坡稳定性的重要指标，我们在野外的时候经常需要快速有效地评价边坡在地震条件下的稳定性，而安全系数是表示边坡稳定性的重要指标，求取地震条件下边坡安全系数的方法有很多，常见的方法有拟静力法、动力时程分析法、动力有限元强度折减法等【2～4】。前人在分析边坡稳定性时大多都是针对具体的边坡情况进行具体的分析【5～7】，其中有少量学者针对具体情况或者片面地研究了地震条件下坡高与安全系数之间的关系，坡角与安全系数之间的关系，以及地震加速度系数与安全系数之间的关系。如高玉峰，范昭平，吴勇信计算了不同地震加速度系数，不同坡高的安全系数，分析了安全系数与坡高之间的关系【8】；郑红雷等采用拟静力法分别计算了下蜀土边坡在水平和竖直方向地震加速度下边坡安全系数与地震加速度系数之间的关系[9]；向志勇等分析了边坡危岩体稳定系数与地震加速度系数之间的关系【10】；刘坤伟等研究了地震和自重两种工况下安全系数与坡角之间的关系【11】。这些学者针对某个具体边坡片面地分析了安全系数随某个或者几个参数的变化关系，没有进行全面系统的分析，所以还没有形成一套能够快速方便地查询边坡动力安全系数，并且适用于任何地方的系统。

在地震或者暴雨临近的时候，抢险应急专家通常要快速地对边坡的稳定性做出评价，用常规的评价边坡稳定性方法（极限平衡法和数值模拟的方法等）进行边坡稳定性评价时，通常需要建模，并需要准确的岩土体力学参数，从而导致常规的边坡稳定性评价方法在评价边坡稳定性时具有速度慢的缺点，故传统的边坡稳定性评价方法并不适合用于应急条件下的边坡稳定性评价，因此，建立适用于应急条件下边坡稳定性快速评价的方法是十分必要的。

本文运用基于极限平衡的动力sarma法来计算不同类型边坡（不同坡高、不同坡角、不同地震加速度系数、不同岩土体力学参数）在地震条件下的动力安全系数，并根据计算结果绘制了相关图件，这使得我们地质工作者在野外能够方便快速地通过查询这些图件来获取地震边坡的动力安全系数，从而为进行地震条件下边坡稳定性的快速评价提供了理论依据。因此，本文的研究是十分有必要。

1 动力sarma法计算原理【12,13】

将边坡划分为若干滑块，块间接触面为倾斜面，第i块受力分析如图1所示。

由水平和垂直方向力的平衡得：

根据Mohr-Coulomb破坏准则有：

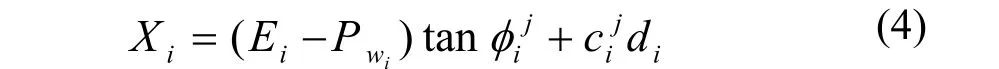
将（3）、（4）、（5）代入（1）、（2）式消去Ti、Xi、Xi+1和Ni可得：

式（6）是个循环式，逐步递推可以得到：

由边界条件En+1=E1=0，得:

其中：

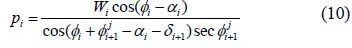
边界条件为：

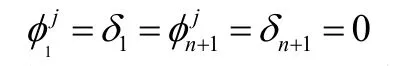
式中：i为块体号；E，X分别为条块侧面上的法向力和切向力，kN；αi为第i块体的条块底面与水平面的夹角（°）；φij为条块左侧界面的平均内摩擦角（°）；φi为条块底面的平均内摩擦角（°）；δi表示条块左侧界面与垂直方向的夹角（°），以竖直向为基准，到界面，顺时针方向为正，逆时针为负，单位（°）；Wi为第i块体的重力（kN）；cij为条块左侧界面的平均粘聚力（kPa）；ci为条块底面的平均粘聚力（kPa）；li为条块底面长度（m）；di为条块左侧界面的长度（m）；Kc为临界加速度系数；Hi为第i块体受到的垂直地震力（kN）；Qi为第i块体受到的水平地震力（kN）；Pwi为滑块左侧面上的孔隙水压力（kN）；Ui为滑块底面上的水压力（kN）。

计算安全系数时，假定安全系数为某个值k，以ci/k代替ci、tanφi/k 代替tanφi、atan(tanφi/k)代替φi、cij/k代替cij、tanφij/k 代替tanφij、a tan(tanφij/k )代替φj，用迭代法根据上述公式计算K和所有未知数。

当Kc=0时的k值即为在边坡受到水平地震力Qi和垂直地震力Hi时的动力安全系数。

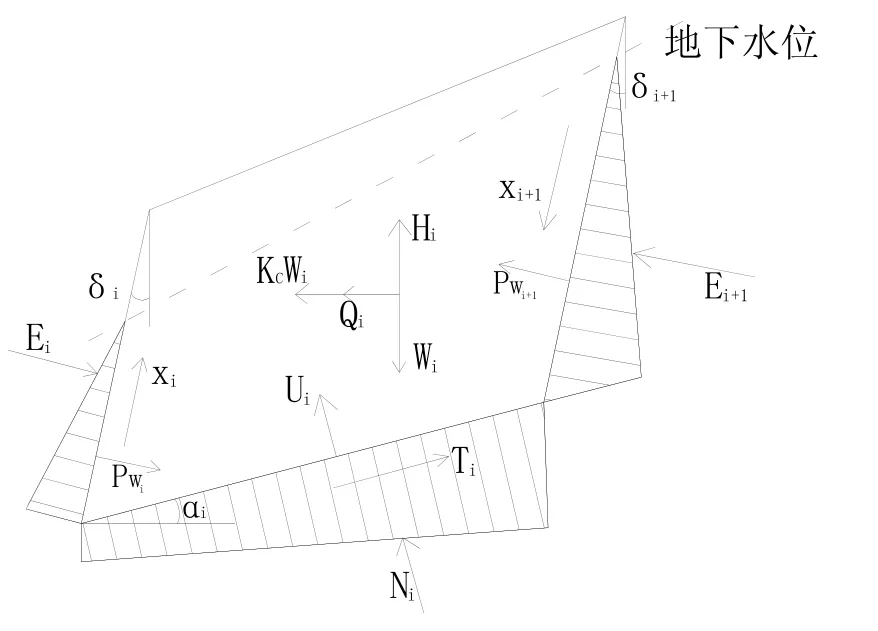
图1边坡滑体受力分析图Fig.1 Force analysis of slope block

2 计算模型及材料参数的选取

研究指定滑面，滑坡体由4个块体组成，取坡高H为50、100、150、200m；坡角α为30°、35°、40°、45°、50°、55°、60°。笔者认为岩体质量等级越高，结构面力学参数也越大，根据工程岩体分级标准GB50218-94【14】，不同类型岩体下，岩体密度和结构面的力学参数取值见表1。滑面取一种结构面参数，条块界面取另外一种结构面参数。研究取14种水平地震加速度系数进行分析，水平地震加速度系数kah为0.05、0.1、0.15、0.2、0.25、0.3、0.35、0.4、0.45、0.5、0.55、0.6、0.65、0.7。研究考虑加速度放大效应，规定从坡脚到坡顶的4个块体的地震加速度放大系数分别为1、1.2、1.5、2。

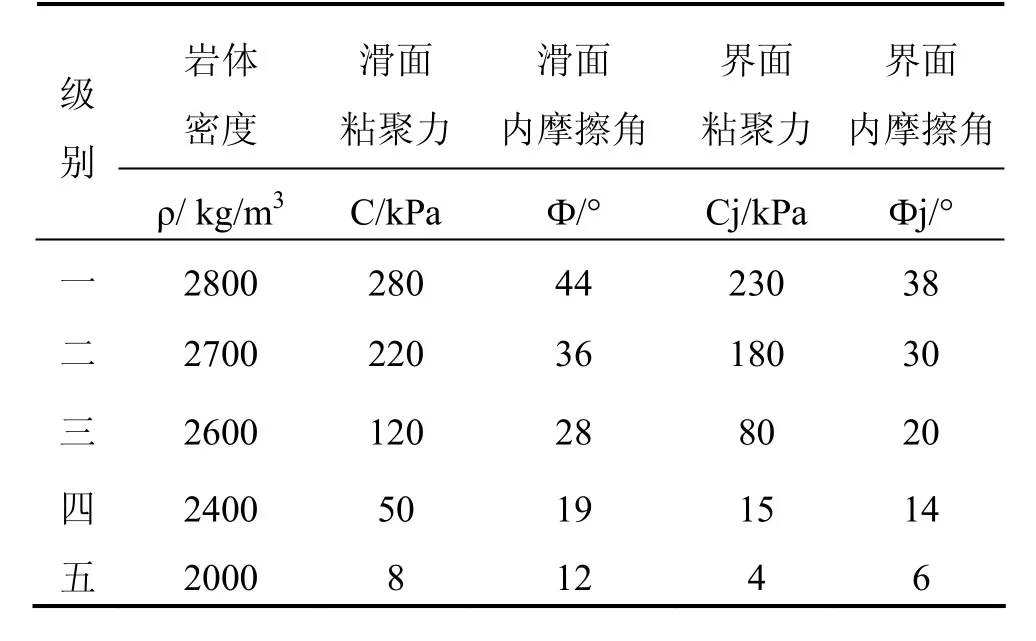
表1 不同类型岩体和结构面对应的力学参数Table 1 Mechanics parameters of rock and structural plane

3 计算结果

当岩体和结构面力学参数取一、二、三、四、五级岩体和结构面力学参数，对于不同坡高、不同坡角的边坡，动力安全系数与水平地震加速度系数之间的变化关系也不同。计算结果中图件比较多，这里就不一一列举出来，只列举了当岩体和结构面力学参数取三级岩体和结构面力学参数时，不同坡高、不同坡角的边坡，动力安全系数与水平地震加速度系数之间的变化关系图，如图2～5所示。动力安全系数用Fd表示，水平地震加速度系数用kah表示。在图2～5的图例中，第一个数字代表坡高，第二个数字代表坡脚，如50～30代表的意思是坡高为50m，坡脚为30°。

图2 取三级参数，坡高为50m时，Fd与kah之间的关系Fig.2 Relation between Fd and kah when slope height is 50m

图3 取三级参数，坡高为100m时，Fd与kah之间的关系Fig.3 Relation between Fd and kah when slope height is 100m

图4 取三级参数，坡高为150m时，Fd与kah之间的关系Fig.4 Relation between Fd and kah when slope height is 150m

图5 取三级参数，坡高为200m时，Fd与kah之间的关系Fig.5 Relation between Fd and kah when slope height is 200m

4 对结果的分析

4.1 坡高对地震边坡安全系数的影响分析

图6为当坡角为45°，水平地震加速度系数为0.2，取各级岩体和结构面力学参数时地震边坡安全系数与坡高之间的变化曲线。可以看出，安全系数随坡高的增加而单调减小，且安全系数的减小速率也随坡高的增加而减小，当坡高为50～100m时，安全系数的变化幅度较大；坡高为100～200m时，安全系数的变化幅度较小。

4.2 坡角对地震边坡安全系数的影响分析

图7为当坡高为100m，地震加速度系数为0.1，取各级力学参数时地震边坡安全系数与坡角之间的变化曲线。可以看出，安全系数随坡角的增加而单调减小，且变化较均匀。

4.3 力学参数对边坡安全系数的影响分析

由图6和图7可以看出，随着岩体和结构面的力学参数增大，边坡的动力安全系数也不断增大。

图6 地震边坡安全系数与坡高之间的关系Fig.6 Relation between safety factor and slope height

图7 地震边坡安全系数与坡角之间的关系Fig.7 Relation between safety factor and slope angle

4.4 地震加速度系数对安全系数的影响分析

由图2～5可以看出，随着水平地震加速度系数的增大，动力安全系数逐渐减小，且安全系数减小的速率随地震加速度系数的增大而不断减小。

5 算例验证

5.1 算例一

边坡为均质岩质边坡，坡高100m，坡脚45°，弹性模量E=20GPa，泊松比μ=0.25，拉力tens=0MPa，容重γ=26kN/m3，粘聚力C=1500kPa，内摩擦角φ=50°，输入的地震波为截取的一段44.62s的振幅被压缩后的东西向卧龙地震波，相应的水平地震加速度峰值ahmax=3.0m/s2，截断频率为7Hz，输入的水平向加速度曲线如图8所示。

图8 输入的水平向加速度曲线Fig.8 Input horizontal seismic acceleration time history

拟静力法计算时，水平地震系数取kh=ahmax/3g【2】，由于ahmax=3.0m/s2，故kh=0.1。由表1可知，例中所用的岩体和结构面力学参数为三级岩体和结构面力学参数，查图3可知kh=0.1时的动力安全系数为0.964。

用有限元强度折减法和动力有限元时程分析法得到的安全系数如表2所示。在有限元强度折减法中，折减系数与关键点水平永久位移的关系曲线如图9所示。由图9可知，当折减系数大于1.6时，关键点水平位移发生突变，因此，由强度折减法确定的边坡安全系数为1.6。

表2 安全系数计算结果Table 2 Computation results of safety factors

图9 折减系数与水平位移之间的关系Fig.9 Relation between reduction coefficient and horizontal displacement

在动力有限元时程分析法中，只考虑水平地震加速度向坡外的情况计算得到的安全系数，不考虑水平地震加速度向坡里时计算得到的安全系数【12】，用动力sarma法计算得到的动力安全系数时程如图10所示。根据动力安全系数时程，可以用不同的评价方法确定不同的安全系数，相应边坡在地震作用下的稳定程度也不同，如表2所示。其中，有限元强度折减法确定的安全系数最大，最小动力安全系数最小，偏差指的是各种评价方法确定的安全系数与本文用sarma法计算得到的拟静力安全系数之间的偏差，由表2可知，本文的方法确定的安全系数与用强度折减法确定的安全系数相差较大，与用动力有限元时程分析法确定的安全系数相差较小，但是与这两种方法相差得都不是很大，因此从计算方法上来说，本文查询系统提供的安全系数与其它评价方法一样都可以用来评价边坡稳定性。

图10 安全系数时程曲线Fig.10 Safety factor time history

5.2 算例二

为了验证本文的安全系数查询系统的实用性，特选取了文献15中列举的边坡（滑坡）实例中的四个边坡实例，根据选取的四个边坡的特征，在本文的系统中查询了其对应的动力安全系数，将查询的安全系数与边坡实际稳定情况和灰类聚类法得出的结果对比可知，通过本文安全系数查询系统得到的地震边坡稳定性与实际边坡在地震条件下的稳定性是一致的，也与王余庆等通过灰类聚类法判断的边坡稳定性是一致的，由此可以说明本文的安全系数查询系统是可以用在实际边坡在地震条件下的稳定性判断中的。边坡基本情况和分析结果见表3。

在表3中力学参数类型指的是岩体和结构面的力学参数类型，倒数第二行是王余庆等用灰色聚类法评价的边坡稳定性，表中的地震加速度系数是通过查询中国地震烈度表[16]得到的地震加速度系数。

表3 实际边坡基本情况及其稳定性判断结果【15,16】Table 3 Basic character of actual slopes and their stability【15,16】

6 结论

（1）本文建立了一个边坡在地震条件下的安全系数查询系统，这使我们能够方便快速地查询坡高为50～200m，坡角为30～60°的边坡在水平地震加速度系数为0.05～0.7时的动力安全系数。

（2）随着水平地震加速度系数的增大，动力安全系数逐渐减小，且安全系数减小的速率随地震加速度系数的增大而不断减小；在坡角、水平地震加速度系数和岩体和结构面力学参数相同时，安全系数随坡高的增加而单调减小，且安全系数的减小速率也随坡高的增加而减小；当坡高、水平地震加速度系数和所取的岩体和结构面力学参数相同时，安全系数随坡角的增加而单调减小，且变化较均匀；当坡高、坡角和水平地震加速度系数相同时，随着所取的岩体和结构面力学参数的减小，动力安全系数也逐渐减小。

（3）当取一级岩体和结构面力学参数，坡高为50m时，在地震加速度系数为0.05～0.7范围内，边坡都是稳定的；当取四级岩体和结构面力学参数，坡高大于100m和取五级岩体和结构面力学参数，坡高大于50m时，在地震加速度系数为0.05～0.7范围内，边坡都是不稳定的；其它情况下都是当坡高、坡角或水平地震加速度系数较大时，边坡不稳定，当坡高、坡角或水平地震加速度较小时，边坡稳定。

（4）本文的方法确定的安全系数与用强度折减法确定的安全系数相差较大，与用动力有限元时程分析法确定的安全系数相差较小，但是与这两种方法相差得都不是很大，因此从计算方法上来说，本文查询系统提供的安全系数与其它评价方法一样都可以用来评价边坡稳定性。

（5）通过用本文提供的动力安全系数查询系统查询实际边坡在地震条件下的安全系数，得出本文查询地震边坡稳定性的结果与实际情况一致，说明本文的安全系数查询系统是可以用在实际边坡在地震条件下的稳定性评价中的。

1 杜晓丽.地震荷载作用下岩质边坡稳定性研究[D]. 导师：戴俊.西安：西安科技大学，2008：1～2

2 叶海林,黄润秋,郑颖人，等.地震作用下边坡稳定性安全评价的研究[J].地下空间与工程学报,2009,5(6):1248～1257

3 刘汉龙，费康，高玉峰.边坡地震稳定性时程分析方法[J].岩土力学，2003，24(4):553～556.

4 郑颖人，赵尚毅，张鲁渝.用有限元强度折减法进行边坡稳定分析[J].中国工程科学，2002，4(10):57～62.

5 晓凡.不同地震烈度下边坡稳定性计算实例[J]. 东北地震研究，1999，15(1)：59～64.

6 何专，姚令侃.地震和暴雨工况下边（滑）坡稳定性分析方法评价[J].水土保持通报，2009，29（3）：178～182.

7 梁力，王伟，李明.某露天矿岩质高边坡地震动力响应及稳定性分析[J].金属矿山，2008，（8）：21～25

8 高玉峰;范昭平;吴勇信.基于Bishop条分法的多点多向地震动作用下边坡稳定性分析[J].防灾减灾工程学报，2010,30（2）：117～122.

9 郑红雷，陆昊，荣泽飞，等.下蜀土边坡地震稳定性分析方法对比研究[J].建筑经济，2009，（增刊）：41～45

10 向志勇，李帅，刘志坚.库车迪那2 井区主干道桥梁四号桥台地基边坡危岩体的地震稳定性分析[J].震灾防御技术，2010,5（3）：326～332

11 刘坤伟，赵冬，蔡庆娥，等.杨青林高边坡地震稳定性分析及治理方案研究[J].中国水运，2010,10（1）：142～143

12 韩庚友.地震条件下岩质边坡反应特性及稳定性研究 [博士学位论文][D]. 导师：王思敬.北京：中国科学院地质与地球物理研究所，2011.

13 陈祖煜，汪小刚，杨健. 岩质边坡稳定分析[M]. 北京：中国水利水电出版社，2005:417～427

14 中华人民共和国水利部. JGJ 50218–94工程岩体分级标准[S]. 北京：中国计划出版社，1995.

15 王余庆，高艳平，辛鸿博.用灰色聚类方法预测边坡地震稳定性研究[J].工业建筑，2002，（6）：44～47

16 中国地震局.GB/T 17742-1999 中国地震烈度表[S].北京：中国标准出版社，2004.

STUDY ON STABILITY OF DIFFERENT TYPES OF SLOPES UNDER SEISMIC CONDITION

He Xiaohei1，Wang Sijing2,3
1. General Institute of Chemical Geology Survey of China Chemical Geology and
Mine Bureau，Beijing，100013，China;
2. Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China; 3. Key Laboratory of EngineeringGeomechanics, Institute of Geology and Geophysics, Chinese Academy of Sciences, Beijing 100029, China)

In this paper, the method of sarma is used to calculate the safety factor of different types of slopes that have different slope height, different slope angle and different mechanics parameters of rock and structural plane under the condition of different horizontal seismic acceleration coeffient, and then a suit of safety factor search system that can be used to look up the safety factor of slopes under seismic condition is established. The results can provide basis for stability estimation of different types of slopes. In addition, the influence of slope height, slope angle, seismic acceleration coeffient, and mechanics parameters of rock and structural plane on the safety factor of seismic slope is also analyzed. Moreover, by comparing the safety factor that is look up in the safety factor search system with the factors that are calculated by other methods, the result shows that the difference between the safety factor that is look up in the safety factor search system and the factors that are calculated by other methods is small, and by using the safety factor search system to evaluate the safety of the actual slopes under seismic condition, the results shows that the evaluation stability is consistent to the actual stability of the slopes.

slope under seismic condition；safety factor；mechanics parameters of rock and structural plane；horizontal seismic acceleration coeffient；method of sarma

TD854.6

A

1006–5296（2014）02–0105–07

① 此文获中化地质矿山总局地质研究院、地质调查总院“第三届青年学术研讨会”论文三等奖

* 第一作者简介：贺小黑(1984～ )，男，主要从事地质灾害、岩土体稳定性及煤层气地质等方面的研究工作，博士，工程师

2014-03-24；改回日期：2014-04-14