Effects of the two-color laser on relativistic muon motion∗

SHI Chun-Hua(石春花),SU Jin(苏晋),and ZHOU Jin-Yang(周晋阳)

1Department of Biomedical Engineering,Changzhi Medical College,Changzhi 046000,China

2Department of Physics,Changzhi Medical College,Changzhi 046000,China

Effects of the two-color laser on relativistic muon motion∗

SHI Chun-Hua(石春花),1,†SU Jin(苏晋),2and ZHOU Jin-Yang(周晋阳)1

1Department of Biomedical Engineering,Changzhi Medical College,Changzhi 046000,China

2Department of Physics,Changzhi Medical College,Changzhi 046000,China

Considering the mixture after muon-catalyzed fusion(µCF)reaction as overdense plasma,we analyze muon motion in the plasma induced by a linearly polarized two-colour laser,particularly,the effect of laser parameters on the muon momentum and trajectory.The results show that muon drift along the propagation of laser and oscillation perpendicular to the propagation remain after the end of the laser pulse.Under appropriate parameters, muon can go from the skin layer into f i eld-free matter in a time period of much less than the pulse duration.The electric-f i eld strength ratio or frequency ratio of the fundamental to the harmonic has more inf l uence on muon oscillation.The laser affects little on other particles in the plasma.Hence,in theory,this work can avoid muon sticking toαeffectively and reduce muon-loss probability inµCF.

Muon,Two-color laser,Overdense plasma,Muon sticking to alpha

I.INTRODUCTION

The muon catalyzed fusion(µCF)of hydrogen isotopes, especially D-T fusion,has been studied as a realizable candidate of an energy source as thermal energies[1–7].In the liquid mixture of D2and T2,the muon plays the role of a catalyzer through the formation of a muonic molecule.After the fusion process,the muon is released normally and again it is utilized for a subsequent fusion until the muon decays.However,in fact,after theµCF,some muon may be strapped byαparticles and form into(αµ)+.This has become a major limitation on the number of fusion cycles catalyzed by each muon[8,9].Because of muon-loss,µCF is far from the aim to attain energy plus.In the past decade,researchers found sticking phenomena and new insights inµCF[10–14],and in experimentsµCF numbers per muon extend to 150 during the lifetime of～2.2×10−6s[15].Althoght this catalyzed eff i ciency is not enough for atomic energy application,muon regeneration from theα-sticking has been increasingly studied.

In this work,we were trying to avoid muon-αsticking by inducting an external force.Here,the laser is a good choice. It is well-known that ultra-short,ultra-intense laser pulses are potentially useful for a variety of applications.Recently, ultra-short lasers have been applied extensively to studies of electron acceleration schemes due to their potential of offering compact and low-cost setups through accelerator gradients several orders of magnitude higher than those of conventional RF linear accelerators[16–18].Unlike one-color laser,a two-color laser beam is the sum of two copropagating pulsed radially polarized laser beams,with central angular frequenciesωandnω,of unequal pulse duration and peak power.Also,the relative phase of the two-color laser pulsesadds one more degree of freedom[19].Previous simulations have shown that a one-color pulsed radially polarized laser beam can accelerate an initially stationary electron only up to 40%of the theoretical energy gain limit[20,21],while a twocolor pulsed beam can accelerate an electron by over 90%of the one-color beam’s theoretical gain limit,for a given total energyandpulseduration[22].So,inordertomakethemuon well out of the mixture,the choice of the two-color laser becomes especially important[23,24].

In this paper,the two-color laser is induced in the D-D fusion,and muon can be moved at a certain track so thatµis not captured byα.To study the muon drift of D-D fusion in the two-color laser,it is necessary to choose some appropriate laser parameters.Here,we explore the possibility of the muon drift and trajectory,particularly;study inf l uences of various laser-pulse parameters(i.e.,frequency,intensity,and relative phase)on the muon drift and investigate coherent effects on other particles in a two-level f i eld.

II.COMPUTATIONAL MODEL AND METHOD

When a cycle ofµCF(d-d):µ+d+d→ddµ→α+n+µis just fi nished,theαandµparticles are existing independently, i.e.theµions are not captured by theαparticles.Then,at the moment,there is the mixture which consists ofα,neutron(n),electron(e),d,andµin the fusion reaction target. It is known that the use of a plasma medium is an attractive way of achieving laser-driven electron acceleration[17].So, we consider the above mixture as the plasma with a frequencyωp,(ω2p=ω2pα+ω2pe+ωp2µ,ωpα,ωpeandωpµare frequency ofα,e andµ,respectively).Also,asωpe≫ωpµ≫ωpα,we judgeωp2=ω2pe.

At the same time of the above mixture formation,the twocolor laser pulse is turned on and off adiabatically,i.e.

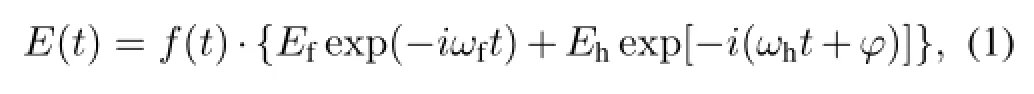
where,subscript f denotes the fundamental part in the twocolor laser pulse and subscript h denotes the harmonic part;EfandEhare amplitude of the electric-f i eld strength of the fundamental laser f i eld and the harmonic f i eld,respectively; for the frequencyωfandωh,thenthharmonic f i eld meansωh=nωf;ϕis the relative phase between the fundamental f i eld and the harmonic;andf(t)is the shape of the laser pulse,i.e.

where,τis the pulse duration.When the plasma frequencyωpmeets the relation ofωp≫ωh>ω(ω=(ωf+ωh)/2 is the equivalent frequency of a two-color laser),the laser beam can be considered propagating in overdense plasma[25].

For the sake of simplicity,we assume that the linearly polarized laser beam propagates perpendicular to the plane surface of the target.Let us direct the axisXalong the propagation of the laser pulse,the axisYalong the electric-f i eld strength,and the axisZalong the magnetic-f i eld strength. Throughout the paper,the system of unitsme=e=c=1 is used.A laser beam propagates in overdense plasma with a plasma frequencyωpgreater than the laser frequencyωin the skin layer having a depthδ=1/ωp.The boundary conditions for the electric and magnetic f i elds on the surface vacuumoverdense plasma are of the well-known form:

where,Finis the electric-f i eld amplitude inside the plasma,F(t)meets the relation ofF(t)=|E(t)|andvarepsilonis the dielectric constant of plasma,i.e.ε=1−ω2p/ω2≈−ω2p/ω2.

Then,the Newton classical equations for muon momentumPxandPyinside the skin layer(x>0)are of the form:

wherek=mµ/me≈207,δ=1/ωpis the depth of the skin layer,andx=0 is the surface of the target.The velocityνxandνyare given by

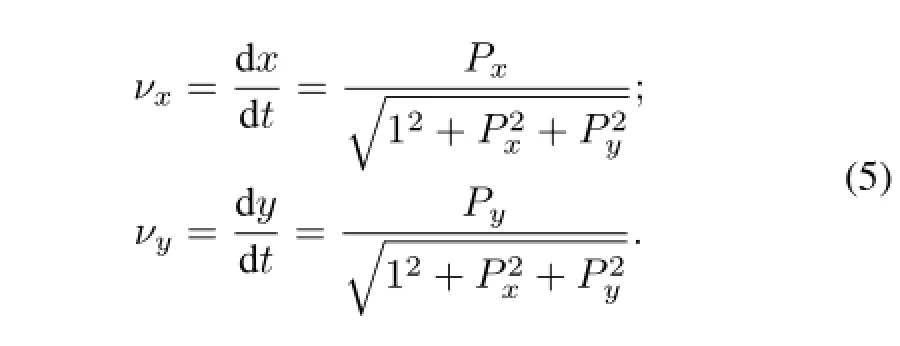
III.NUMERICAL RESULTS AND ANALYSIS

We assume that there is no muon motion along the magnetic-f i eld strength,i.e.the axisZ.Besides,collisions of muons are neglected in our consideration.Eqs.(4)and(5) can be solved with the initial conditions that at the time instancet=−∞a muon is at rest whenx=y=0.Of course, the average muon velocity along theYaxis is zero.After the end of a laser pulse,a muon has zero velocity in theYdirection and nonzero velocity in theXdirection.

A.The effect of electric-f i eld strength

The relativistic plasma frequency isωp=(4πne/γ)1/2,γ=[1+(Fin/ω)2]1/2is the relativistic factor.From Eq.(1) to Eq.(5),we f i xed the valueωp/ωf=21/2 andωfτ/π=40 in our numerical computation which correspond to the pulse durationτ=83fs and the electron number densityne= 8×1022cm−3.For the two-color laser,we take the 2thharmonic f i eldωh=2ωfand the relative phaseϕ=0.Based on the above values,by solving the Eqs.(4)and(5),the muon motion is determined only by one dimensionless parameterg=4Ef/(3ωf)and the amplitude ratio of the electric-f i eld strengthEf/Eh.The valueg=1 corresponds to the peak laser intensity of 5×1017W/cm2(at the laser photon energy ħω=1.5eV).

Fig.1.The dependences of the muon momentumPxon the dimensionless parameterg.

Figure 1 shows the dependence of muon momentumPx(in units ofmec,in this paper,the units of the momentum are allmec.)on the value of g and the different ratio ofEftoEh, where we takeEh=Efand 3Eh=Ef,respectively.The valuegfrom 0 to 100 corresponds to the peak laser intensity of 0～5×1021W/cm2.The results show that the two curves change in a similar way basically.The momentum increases with the laser intensity,but it is a nonrelativistic quantity(Px≪mec)even at the relativistic peak laser intensity 5×1021W/cm2.Fig.1 also shows the different ratio of the fundamental electric-f i eld strength to the harmonic has effects on the muon momentumPx,but the effect is obviousatg=0～70 and is not obvious atg>70.

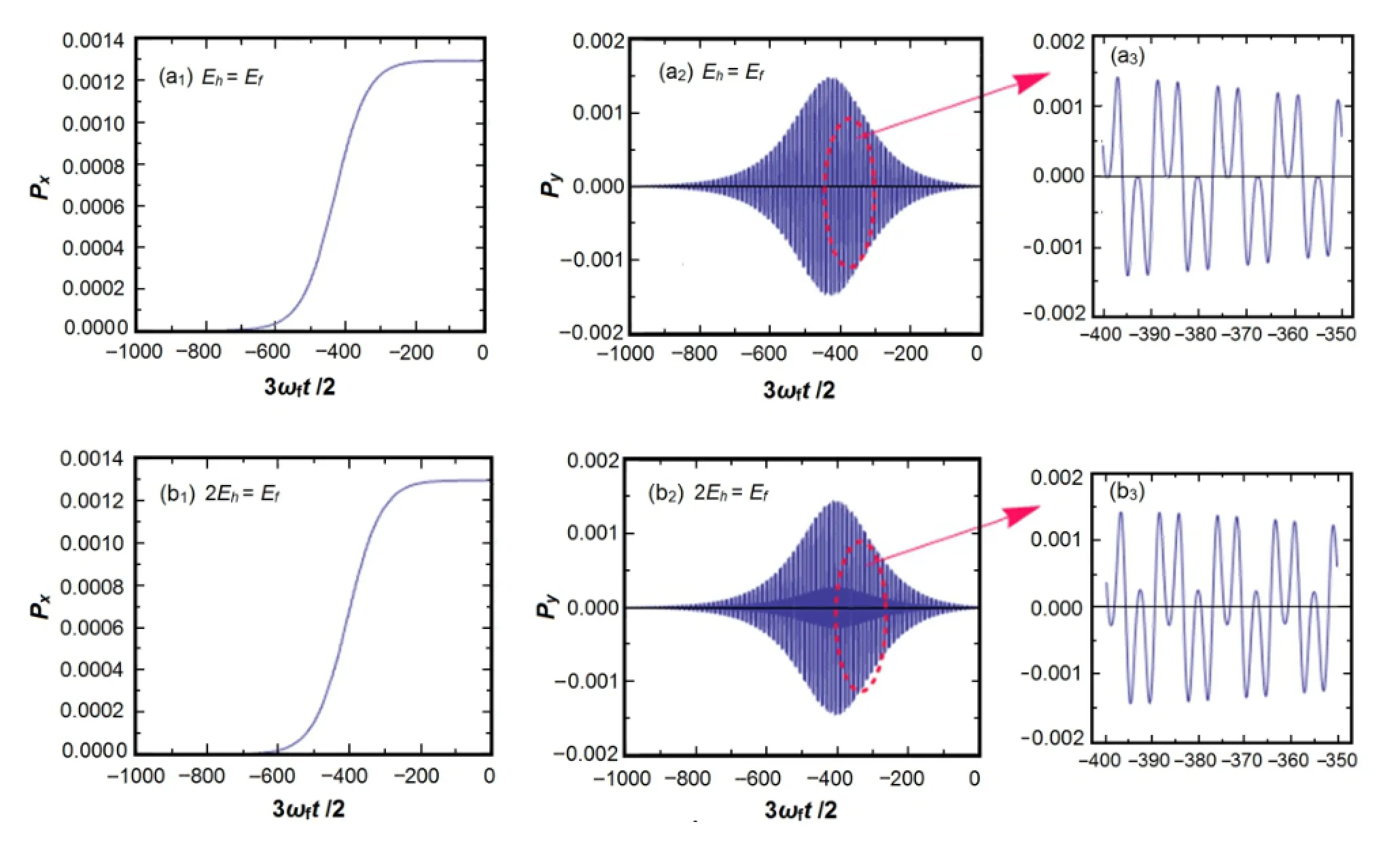
Fig.2.(Color online)The muon momentumPxandPychange for the value of the dimensionless parameterg=80.

Figure 2 demonstrates the muon momentumPxandPyat the leading edge of the laser pulse for the typical value ofg=80(the peak laser intensity of the fundamental wave is 3.2×1021W/cm2according to Eqs.(4)and(5),withEh=Efin Fig.2(a1–a3)and 2Eh=Efin Fig.2(b1–b3).As can be seen in the f i gures,a muon goes from the skin layer inside f i eld-free matter before the laser pulse(∝sech2(t/τ)) reaches its maximum because of the small depth of the skin layer.i.e.a muon stops acceleration on the rear border of the skin layer.It is also obvious thatPy→0 when a muon leaves theskinlayer,becauseofadiabaticityofthelaserpulse.Inaddition,the differentEf/Ehratio affects little on the muon momentumin theXaxis,but obviouslyintheYaxis(Figs.2(a3) and 2(b3)).

The muon trajectory in the plane forg=80 is shown in Fig.3.The dimensionless muon coordinatesxandyare given in units of the skin depthδ.The amplitude of muon oscillations in the transverse directionYis much less than its drift motion in the direction of laser pulse propagation(theXaxis).This indicates that a muon penetrates many skin depths into f i eld-free matter even before the laser pulse reaches its maximum.The amplitude and shape of muon oscillations in the transverse directionYin Figs.3(a)and 3(b)differ from each other,due to different harmonic wave electric-f i eld strength.At a greaterm=Ef/Eh,the amplitude of muon oscillations in the transverse directionYreduces and the shape is more complicated.

Fig.3.(Color online)The muon trajectory.

Fig.4.(Color online)The muon motion in one-color laser f i eld.

To explain that a muon goes from the skin layer inside fi eld-free matter or penetrates many skin depths into fi eldfree matter before the laser pulse reaches its maximum,we make an estimate qualitatively.We consider that the muon drift velocity in the direction of laser pulse propagation has the estimateνx=N(Ef/ωp)2from Eq.(4).Then,the timetpfor penetration of the skin layer having the depthδis approximately,i.e.tp=δ/νx=ωp/(NEf2)≈48fs.The result showstp<τ,i.e.the timetpat which a muon goes into fi eld-free matter from the skin layer is much less than the laser durationτ.Thus,a muon goes quickly from the skin layer into fi eld-free matter.

Besides,in order to better illustrate effects of the two-color laser intensity on muon motion,we calculate the muon momentum and trajectory in one-color laser(Fig.4,in a peak laser intensity of 6.4×1021W/cm2and other parameters being the same value as the above.In Fig.4(c)the maximum of muon momentumPxin the one-color laser fi eld is less than in Fig.2(a1).It shows that the in fl uence of the two-color laser intensity on the momentum is not a simple addition of two one-color laser beams,and a two-color pulsed beam can accelerate muon to the same maximum with lower intensity. In Figs.4(a)and 4(b),the oscillations of muon momentumPyin the one-color laser fi eld are different from Fig.2(a2) and 2(a3).The muon oscillations have just one peak in every cycle in one-color laser fi eld(Fig.4(b))but two peaks in two-color laser fi eld(Fig.2(a3)).The muon trajectory in the one-color laser fi eld is shown in Fig.4(d),where the amplitude of muon oscillations in the transverse directionYis obviously less than that in the two-color laser fi eld(Fig.3(a)). In Fig.3(a),the muon oscillation in each cycle has two peaks (red and black arrows)in the two-color laser fi eld,but in Fig.4(d)it has a single peak(red arrow).Certainly,in the one-color laser fi eld,a muon goes from the skin layer inside fi eld-free matter before the laser pulse reaches its maximum, andPy→0 when a muon leaves the skin layer.However,a muon takes a longer time to go into fi eld-free matter from the skin layer in the one-color fi eld than in the two-color fi eld.

B.The effect of frequency

To evaluate the frequency effect,we still fi x the pulse durationτ=83fs and the electron densityne=8×1022cm−3. For the two-color laser,we take 2Eh=Ef,Ef= 8.0×1020W/cm2andϕ=0.Therefore,the muon motion is determined only by the dimensionless parameterωp/ω(ω= (ωf+ωh)/2)and the frequency ratio of the fundamental laser fi eldωfto the harmonic fi eldωh.

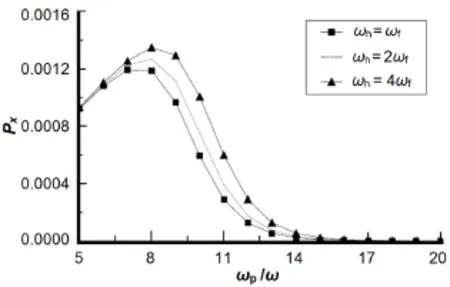
Fig.5.The dependences of the muon momentumPxon the dimensionless parameter ofωp/ω.

Figure 5 shows the dependence of muon momentumPxonωp/ω,and onωf/ωh,atωh=ωf,ωh=2ωfandωh= 4ωf,respectively.Theωp/ωchanges from 5 to 20 so that the plasma frequencyωpis far larger than the laser frequencyω. In Fig.5,the three curves change in a similar way basically, but different frequency ratio affects the muon momentumPx, especially atωp/ω=6～14.Besides,the three curves have different peak positions.

Figure6showsthemuonmomentumPxandPyattheleading edge of the laser pulse for typical value of the peak laser intensity of the fundamental wave being 8.0×1020W/cm2andωp/ω=8 according to Fig.5.We takeωh=2ωfin Figs.6(a1)and 6(a2)andωh=4ωfin Figs.6(b1)and 6(b2). Fromthef i gures,amuongoesfromtheskinlayerinsidef i eldfree matter before the laser pulse reaches its maximum,andPy→0 when a muon leaves the skin layer.In addition, the frequency ratio affects the muon momentum obviously in theXaxis and theYaxis.At a higher frequency ratio,i.e.a greatern=ωh/ωf,the maximum of the muon momentumPxincrease,and so does the amplitude of the muon oscillations ofPyin theYaxis,with a more complicated shape.

Figure 7 shows the muon trajectory in the plane for the peak laser intensity of fundamental wave 8.0×1020W/cm2andωp/ω=8.The dimensionless muon coordinatesxandyare given in units of the skin depthδ.The amplitude of muon oscillations in the transverse directionYis much less than its drift motion in the direction of laser pulse propagation(theXaxis).This indicates that a muon penetrates the skin depths into f i eld-free matter even before the laser pulse reaches its maximum.At a greatern=ωh/ωf,with an increased muon momentum in theXand theYaxises,the amplitude of muon oscillations in the transverse directionYincreases while the frequency of muon oscillations reduces.Thus,the muon oscillations in theYaxis reduce and at the same time the muon leaves the skin layer by a faster speed in theXaxis.

In the same way,based on above parameters,the timetpat which a muon goes into f i eld-free matter from the skin layer is about 44fs.A smaller-than-τ tpmeans that a muon penetrates the skin depth into f i eld-free matter before the laser pulse reaches its maximum.So,the muon leaves the skin layer faster to enter the free f i eld,atωp/ω=8 and peak laser intensity ofEf=8.0×1020W/cm2,than the results in Sec.III.A at much larger parameters ofgandEf.

C.The effect of relative phase

For the two-color laser with the parameters ofωp/ω=8,Ef=8.0×1020W/cm2,electron number densityne= 8.0×1022cm−3,2Eh=Efandωh=2ωf,the muon motion is determined only by the pulse durationτand the relative phaseϕ.The relative phase in two-color lasers means the propagation distance in the plasma media.It can be converted into the media lengthL=ϕλh/(2π).

Figure 8 shows the muon momentumPxat the relative phase ofϕ=π/6(L=λh/12)and the pulse durationτ=10～100fs.Atτ<50fs,the muon momenturmPxis less than those in Sec.III.A and Sec.III.B,hence a longertp, the time for penetrating the skin layer of the depthδ.Then, probably,once the laser pulse duration is less than 50fs,the muon cannot penetrate the skin layer at the end of a pulse. Thus,to study the effect of the relative phase on the muon trajectory,we takeτ=50fs.

Figure 9 shows the muon momentumPyat the leading edge of the laser pulse,with peak laser intensity of the fundamental wave being 8.0×1020W/cm2atωp/ω=8,τ= 50fs,and the relative phaseϕ=0(L=0),π/4(L=λh/8),π/2(L=λh/4)and 3π/4(L=3λh/8).We also f i nd that the relative phaseϕhas obvious effects on the muon momentum in just theYaxis.The muon oscillations shape and the peak change with the relative phase.The red and the black arrows indicate peaks that change constantly with the relative phase.Because the relative phase has less effect on the muon momentumPx,the muon trajectories are similar to the results above.The muon speed in theXaxis is not affected and the muon still can penetrate skin depths into f i eld-free matter.However,as shown in Fig.10,in the transverse directionY,the muon oscillations are in different amplitudes and shapesatdifferentrelativephases.InFigs.9and10,atgreater the relative phases,the muon oscillation peaks marked with red arrows increase while the muon oscillation peaks marked with black arrows reduce consistently.

D.The effects of muon initial velocity

For all above analysis,initial velocity of muon is neglected in our consideration,i.e.Eqs.(4)and(5)can be solved with the initial conditions thatν(t=−∞)=0.In fact,after everyµCF reaction,velocity of muon is not zero but its value is not unique.Most muons are free,and their velocity depends on the energy release of nuclear fusion[13].Some muons stick to alpha particlesandform muonic helium ions,and theinitial sticking probability is 0.912%[26].Where muonic helium ions are formed with energy of 3.47MeV,they are slowed down toward thermal energy by collision with the surrounding D2and DT molecules[27].So,muonic helium ions can be stripped as a result of collisions and some muons regain free,probability of which is 25%[28].Their velocities are much less.Other muonic helium ions may be stripped by theexternal force[29]and velocity of free muon are related to the force.Based on the energy release of nuclear fusion,we take two value of initial velocity and solve the Eqs.(4)and(5).

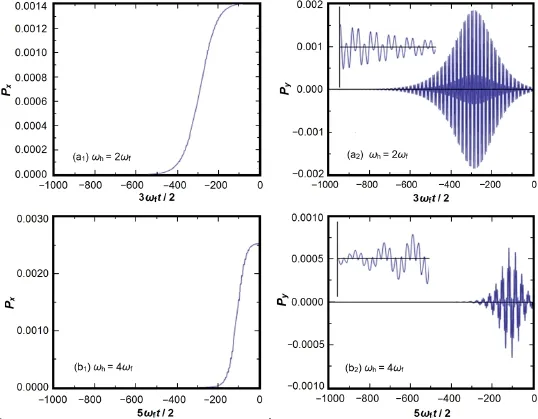
Fig.6.(Color online)The muon momentumPxandPychange for the value of the dimensionless parameterωp/ω=8.

Fig.7.(Color online)The muon trajectory.

Fig.8.The dependences of muon momentumPxon the pulse durationτat the relative phase ofϕ=π/6.

Figure 11 shows the muon momentumPxandPyat the leading edge of the laser pulse and where values of relevant parameters are the same with Fig.2(a1−a3).The only different is the value of muon initial velocity.According to Eqs.(4) and(5),we take the initial velocityνx=νy=0.001 in Fig.11(a1–a3),andνx=νy=0.0001 in Fig.11(b1–b3), instead ofνx=νy=0 in Fig.2(a1−a3),the unit of velocity isc=3×108m/s.The results shows that a muon goes from the skin layer inside f i eld-free matter before the laser pulse reaches its maximum,andPy→0 when a muon leaves the skin layer.Comparing Figs.11(a3)and 11(b3),the detail changes ofPy,the muon initial velocity has obvious effect onthe muon momentum in theYaxis,while it has a little effecton the muon momentum in theXaxis.In the case of super-intense laser pulses,the initial velocity in theXaxis plays a little role in muon drift,for muon has relatively high drift velocities induced by the laser in theXaxis.

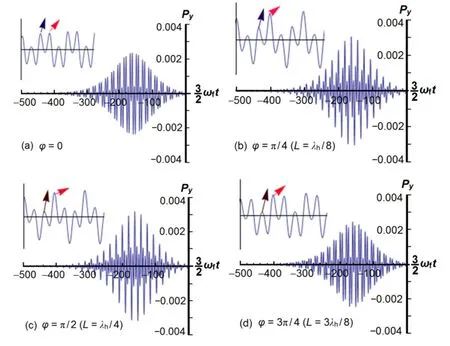
Fig.9.(Color online)The muon momentumPychange for the pulse durationτ=50fs.

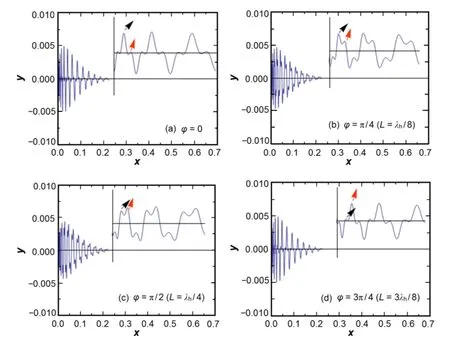
Fig.10.(Color online)The muon trajectory.

Fig.11.The muon momentumPxandPyatg=80 in muon initial velocity of 0.001cand 0.0001c(c=3×108m/s).

IV.DISCUSSION AND CONCLUSION

In addition,with the induction of the two-color laser,we have to consider the inf l uence of the laser on other particles in the overdense plasma.According to similar methods,we study the other particles trajectory in different muzzle velocities.Because the muzzle velocity of other particles is small, the laser has little inf l uence on them,i.e.the motion of those particles produced by the superintense laser pulse is far less than the motion of muons.Also,the duration of laser pulse is so short that the work does not introduce the disadvantage intoµCF reaction in the superintense laser,but make the muon penetrate skin depths into f i eld-free matter to avoid theα-sticking.

In this paper,we consider the mixture afterµCF(d-d)reaction as overdense plasma with the frequencyωp,and the twocolor lasers with the frequencyωhandωfare induced.We study the effect of two-color laser parameters on the muon momentum and trajectory,including the peak intensity,ratio of the fundamental electric-f i eld strength to the harmonic, frequency ratio,relative phase and pulse duration.We f i nd that the time at which a muon penetrates into f i eld-free matter from the skin layer is much less than the pulse durationτunder the right conditions.This penetration occurs at the leading edge of the laser pulse.The muon drift in overdense plasma along the propagation of laser radiation produced by a magnetic part of a laser f i eld remains after the end of the laser pulse.Hence,afterµCF(d-d)reaction is f i nished and before the muon is captured byα,inducting a suitable superintense laser pulse can avoid theα-sticking eff i ciently.

[1]Gershtein S S,Petrov I V,Ponomarev L I,et al.Zh Eksp Teor Fiz+,1980,78:2099–2111.

[2]Alexander S A,Froelich P,Monkhorst H J.Phys Rev A,1990,41:2854–2857.

[3]Ponomarev L I.Contemp Phys,1990,31:219–245.

[4]Petitjean C,Atchison F,Heidenreich G,et al.Fusion Technol, 1994,25:437–449.

[5]Nagamine K,Matsuzaki T,Ishida K,et al.Hyperf i ne Interact, 1999,119:273–280.

[6]Nakamura S N,Nagamine K,Matsuzaki T,et al.Phys Lett B, 2000,473:226–232.

[7]Nagamine K.Nucl Energy,2005,3B:555–602.

[8]Ceperley D and Alder B J.Phys Rev A,1985,31:1999–2004.

[9]Davies J D,England J B A,Pyle G J,et al.J Phys G Nucl Partic,1990,10:1529–1537.

[10]Ishida K,Okamoto K,Kawasaki Y,et al.Phys Rev Lett,2002,89:107202.

[11]NagamineKandPonomarevL.NuclPhysA,2003,721:c863–c866.

[12]Ishida K,Nagamine K,Matsuzaki T.Nucl Phys B,2005,149: 348–350.

[13]Kimura S and Bonasera A.Radiat Eff Defect S,2008,163: 287–292.

[14]Balin D V,Ganzha V A,Kozlov S M,et al.Phys Part Nuclei, 2011,42:185–214.

[15]He J T.Physics,2003,18:461–466.(in Chinese)

[16]Malka V,Faure J,Gauduel Y A,et al.Nat Phys,2008,4:447–453.

[17]Esarey E,Schroeder C B,Leemans W P.Rev Mod Phys,2009,81:1229–1285.

[18]SalaminYI,HuSX,HatsagortsyanKZ,etal.PhysRep,2006,427:41–155.

[19]Shi C H,Qiu X J,Li R X.J Mod Optic,2007,54:1435–1444.

[20]Wong L J and K¨artner F X,Opt Express,2010,18:25035.

[21]Fortin P L,Pich´e M,Varin C.J Phys B,2010,43:025401.

[22]Liang J W and Franz X K.Opt Lett,2011,36:957–959.

[23]Zhao K and Chu T S.Chem Phys Lett,2011,511:166–171.

[24]Johnson L A,Palastro J P,Antonsen T M,et al.Phys Rev A, 2013,88:063804.

[25]Rastunkov V S and Krainov V P.Phys Rev E,2004,69: 037402.

[26]Hu C Y,Hale G M,Cohen J S.Phys Rev A,1994,49:4481–4488.

[27]Jones S E.Nature,1986,321:127–133.

[28]Zeldovich Y B and Gershtein S S.Sov Phys Uspekhi,1961,3: 593–623.

[29]Shi C H,Qiu X J,An W K,et al.Acta Phys Sin,2005,54: 4087–4091.(in Chinese)

10.13538/j.1001-8042/nst.25.020201

(Received October 24,2013;accepted in revised form December 17,2014;published online April 20,2014)

∗Supported by Natural Science Foundation of Scientif i c and Technological Innovation Programs of Higher Education Institutions in Shanxi(No.20091025)

†Corresponding author,shi-chunhua@163.com