A method for determination of the s orbital component of12Be ground state∗
CAI Xiao-Lu(蔡晓鹭),FAN Guang-Wei(樊广伟),XU Hang-hua(许杭华),AN Zhen-Dong(安振东),FAN Gong-Tao(范功涛),XU Ben-Ji(徐本基),LI Yong-Jiang(李永江),Pan Qiang-Yan(潘强岩),YAN Zhe(阎吉吉),and XU Wang(徐望)
1Shanghai Institute of Applied Physics,Chinese Academy of Sciences,Shanghai 201800,China
2University of Chinese Academy of Sciences,Beijing 100049,China
3School of Chemical Engineering,Anhui University of Science and Technology,Huainan 232001,China
4Shanghai Synchrotron Radiation Facility,Chinese Academy of Sciences,Shanghai 201204,China
A method for determination of the s orbital component of12Be ground state∗
CAI Xiao-Lu(蔡晓鹭),1,2,†FAN Guang-Wei(樊广伟),3XU Hang-hua(许杭华),1,2AN Zhen-Dong(安振东),1,2FAN Gong-Tao(范功涛),1XU Ben-Ji(徐本基),1LI Yong-Jiang(李永江),1Pan Qiang-Yan(潘强岩),4YAN Zhe(阎吉吉),1and XU Wang(徐望)1
1Shanghai Institute of Applied Physics,Chinese Academy of Sciences,Shanghai 201800,China
2University of Chinese Academy of Sciences,Beijing 100049,China
3School of Chemical Engineering,Anhui University of Science and Technology,Huainan 232001,China
4Shanghai Synchrotron Radiation Facility,Chinese Academy of Sciences,Shanghai 201204,China
The ambiguity of the structure of12Be especially in the conf i guration of12Be ground state has attracted a lot of attention recently.We notice that the nuclear reaction cross sectionσRat low energy region is sensitive to the surface structure of12Be,which is greatly impacted by the ground state conf i guration of12Be especially by the occupancy probability of thesorbital component.By using existed interaction cross section data of12Be on C at 790MeV/nucleon and Glauber model,the upper limit of thesorbital occupation probability of12Be ground state is roughly determined to be about 56%with Single Particle Model calculations.This demonstrates that the method is very promising to determine thesorbital component of12Be with proper nuclear-matter density distribution calculations for different orbitals of12Be ground state.Hence we bring forward to determine thesorbital component of12Be by measuring theσRof12Be on C and Al at several tens of MeV/nucleon.In this paper,the feasibility and detailed experimental scheme of theσRmeasurement are carefully studied.The precision of thesorbital occupation probability of12Be ground state is expected to achieve 9%by using the proposed 2%σRdata.
12Be,Density distribution,MOL[FM],Ground state conf i guration
I.INTRODUCTION
During the past decades,studies on exotic nuclei have been stimulated considerably owing to the enormous development of radioactive ion beam(RIB)technique.Many peculiarities of exotic nuclei have been revealed,such as the halo/skin-like structure[1],the cluster structure[2]and the breakdown of shell closure[3,4].Studies on these peculiarities greatly improved understanding of the exotic nuclei,e.g.the beryllium isotopes.Theoretical researches on properties of Be isotopes are based on the three-body model[5,6]and the densitydependent relativistic mean-f i eld model[7,8].The neutron halo of14Be has been well explained using these models[5–8].Located between the halo nuclei11Be and14Be,12Be is an interesting combination of the peculiarities and plays a key role in the beryllium chain.In shell model,12Be is supposed to be a“magic nucleus”with simple structure.But recent experiments[4,9,10]provided direct evidence for breakdown of theN=8 shell closure in12Be and the(s,d)intruder states.In principle this intruder-state conf i guration can cause halo-like structure,yet neither the wide momentum distribution[11]nor the relative large two-neutron separation energy (S2n=3.67MeV[12])indicates the signature for a halo. There exists controversy between the recent theoretical and experimental results on halo-like structure of12Be.The gi-ant deformation in the ground state of12Be[13]is also predicted by Antisymmetrized Molecular Dynamics(AMD),the ground state structure of12Be is still ambiguous.Also,explorations in the level structure,parity,spin and deformation of the excited states of12Be with molecular cluster model draws quite a lot of attentions[14–18].The ground state structure properties of12Be are indispensable in the studies because it provides fundamental information for the studies of the excited states.Therefore,it is of signif i cance to study the ground state structure of12Be.
As an essential property of the ground state structure,the nuclear-matter density distribution of12Be not only provides basic structure information such as nuclear-matter radius,but also helps to determine whether the12Be ground state has a halo structure.Recently,particle-particle random-phase approximation(pp-RPA)[19]and microscopic no-core shellmodel(NCSM)calculations[18]have shown that the ground state wave functions of12Be are dominated by thepshell conf i guration,which is in conf l ict with the previous calculations[20–24]and the knockout measurements[4,9].The nuclear-matter density distribution may be used to determine the conf i guration mixing between the 1p1/2,1d5/2and 2s1/2orbitals,thereby help to resolve the inconsistencies between current data and various theoretical models.Therefore,we were motivated to determine the nuclear-matter density distribution of12Be ground state.
In the following text,the experimental method of theσRmeasurement is introduced in Sec.II,the feasibility analysis and optimization of the reaction cross section(σR)measurement are elaborated in Sec.III,the way to determine thesorbital component of12Be ground state throughσRis illustrated in Sec.IV,and a summary is given in Sec.V.
II.GENERAL SCHEME
Typically the nuclear-matter density distribution is investigated by measuring theσR(or the total interaction cross sectionsσI).This involves theoretical models,and several methods were developed to study the total reaction cross section, such as the multi-step scattering theory of Glauber[25],the transport model method of Maet al.[26,27]and the semiempirical formula of Koxet al.[28]and Shenet al.[29] A series of investigations to12Be were carried out in the past decades.By measuring theσIon Be,C and Al at 790MeV/nucleon,Tanihataet al.successfully determined the effective root-mean-square(RMS)radius of12Be through a Glauber model in 1988[30].Liatardet al.measured theσRof radioactive Be isotopes on Cu at around 25 to 65MeV/nucleon and deduced the radii by using a simple microscopic model[31].Later,Warneret al.measured theσRof12Be on Pb and Si at about 30 to 60MeV/nucleon and obtained the radius of12Be[32].However,the studies have several drawbacks.First,their energy region did not cover both low and high energy regions.Data at low energy region give constraint to the outer structure,and data at high energy region provide more information on the core part,hence low and high energy region data are both needed to obtain accurate nuclear-matter density distribution.Second,generally, their targets were too heavy.This makesσRinsensitive to the surface structure of12Be.Third,their models were too simple to interpret the data especially at low energies.The results did not give detailed nuclear-matter density distribution of12Be especially for the surface area.
In obtaining detailed outer structure of the nuclei,two improvements were made recently for extracting accurate nuclear-matter density distribution of nuclei.First,the method of proton elastic scattering at intermediate energies was developed.Ilievaet al.applied proton-scattering method in 2012 to12Be[33]and determined the nuclear-matter density distribution of12Be ground state.But the result has considerable uncertainty because of various parametrizations.So the method is not well established yet for studing the surface structure of especially unstable nuclei.Second,the applicability of Glauber model in the whole energy region was studied and a Modif i ed Optical Limit Glauber model(MOL[FM]) was developed by incorporating the Fermi motion of nucleons in the f i nite-range MOL[34].The MOL[FM]has reduced the discrepancy between the data of calculation and measurement to just 1%–2%for the whole energy region.By measuring theσRon Be,C and Al targets at intermediate energies,the nuclear-matter density distributions of22C[35] and17Ne[36]were determined accurately with MOL[FM]. Through this method we obtained the nuclear-matter density distribution of8Li[37]precisely and the relevant paper about our further study is in preparation.Therefore,MOL[FM] provides a powerful tool for interpreting theσIorσRdata, and measuring theσIorσRdetermining the nuclear-matter density distribution with MOL[FM]is still a good method at present.
Thus,we were motivated to precisely measureσRof12Be at low energy region and extract the nuclear-matter density distribution of12Be ground state using MOL[FM].
Refer to the measurements ofσR,transmission method is usually used.Typical experimental procedures are given in Ref.[38].TheσRis obtained by Eq.(1),
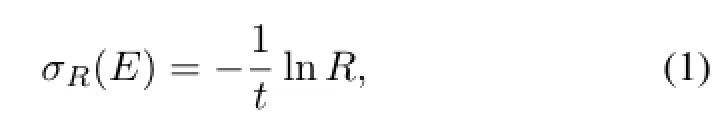
whereEis the energy point;tis the target thickness expressed by the target particles numbers per unit area;andR=Nout/Ninis the ratio of outgoing projectile particles number to incident projectile particles.Since energy of the projectile particles decreases as passing through the target, we determine the energy point ofσRby mean energyEmean, which is given by
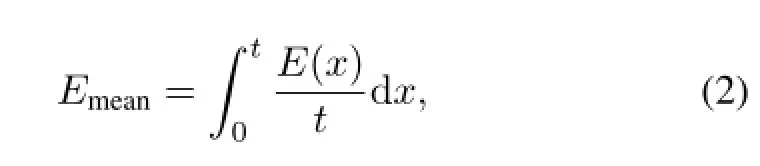
wheretis the target thickness,andE(x)is the residual energy of incident beam travelling along the path by distancex.E(x)can be calculated by the improved Bethe-Bloch formula[39].
The main relative error ofσRcan be written as

where Δt/tstands for uncertainty of the target thickness,the subscripts“sys”and“stat”denote the systematic and statistical error ofR,respectively,and the statistical error ofRis given by
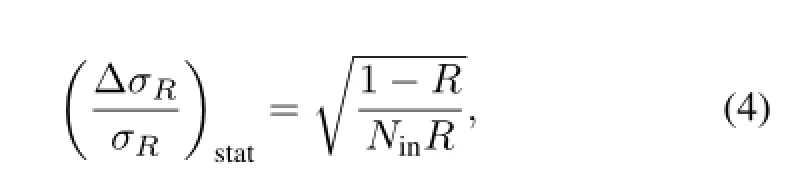
because it follows the binomial distribution.In practice,Rin/Routis taken asRin order to remove the events interact outside the target,RinandRoutare the ratios ofNout/Nincorresponding to the target-in and target-out measurements, respectively.Accordingly,the relative error ofσRbecomes
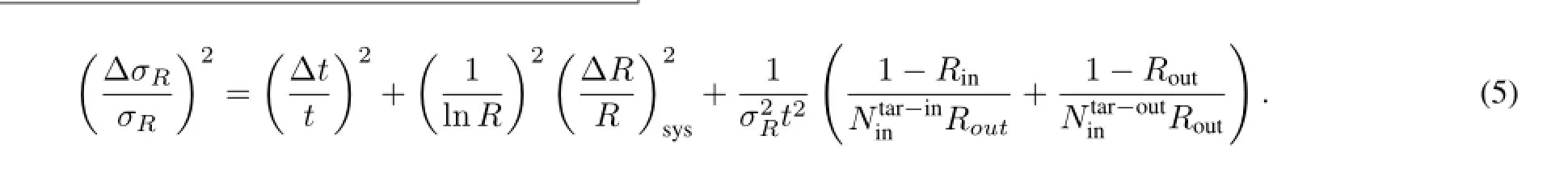
Besides the contribution of statistical error,the systemicuncertainty ofσRis mainly from the correction of the num-ber of inelastic-scattering events merged into the non-reaction events.By using the method in Ref.[40]and Monte Carlo simulation,the systematic error ofσRcan be limited within 1%–2%[34].So 1%–2%total uncertainty can be achieved if suff i cient reaction events are recorded.In fact,this was achieved recently in most experiments of the kind.
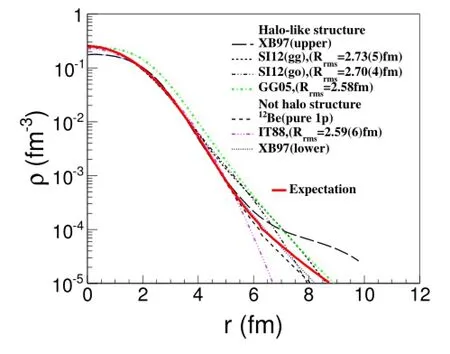
Fig.1.(Color online)Current results of the nuclear-matter density distributions of12Be(XB97:[41],SI12:[33],GG05:[42], IT88:[30]).The solid line is given by the sum of the nuclear-matter density distribution of10Be core in ref.[33]and that of two valence neutrons calculated in section 4 with the conf i guration in ref.[4].
Based on available nuclear-matter density distributions of12Be from experiments and theories(Fig.1),we calculated theσR(Fig.2)at different energies by MOL[FM]. The momentum width and the f i nite-range parameterβwere taken from Ref.[34].From Fig.2 one sees that below~50MeV/nucleon,σRdata with uncertainty around 2%is suff i cient to distinguish several previous results and determine whether12Be has a clear halo-like structure.
However,the specif i c requirement on experimental conditions for a 2%precision ofσRis still unknown,and investigation is needed for further discussion of the method’s feasibility.
III.FEASIBILITY STUDY AND OPTIMIZATION OF σRMEASUREMENT
Tomakesurethattheexperimentispractical,wehavestudied the feasibility and optimized the experimental method. The experiment feasibility mainly relies on detecting system, reaction targets and12Be beam.In the energy region below 50MeV/nucleon,ΔE−Emethod is often used for particle identif i cation.The required energy deposition of12Be in the ΔEdetector is about 10MeV/nucleon,while the required energyintheEdetectorshallbeabove10MeV/nucleon,justfor ensuring validity of the particle identif i cation.So the energy of12Be right before the ΔEdetector is supposed to be over 20MeV/nucleon.Usually Si detector and scintillator detector are used as the ΔEandEdetector,respectively.Their thicknesses depend on the specif i c energy of12Be right before the ΔEdetector.As for the particle identif i cation before the reaction target,Bρ-ΔE-TOF technique is often used.Typical layout of the detecting system is shown in Fig.3.
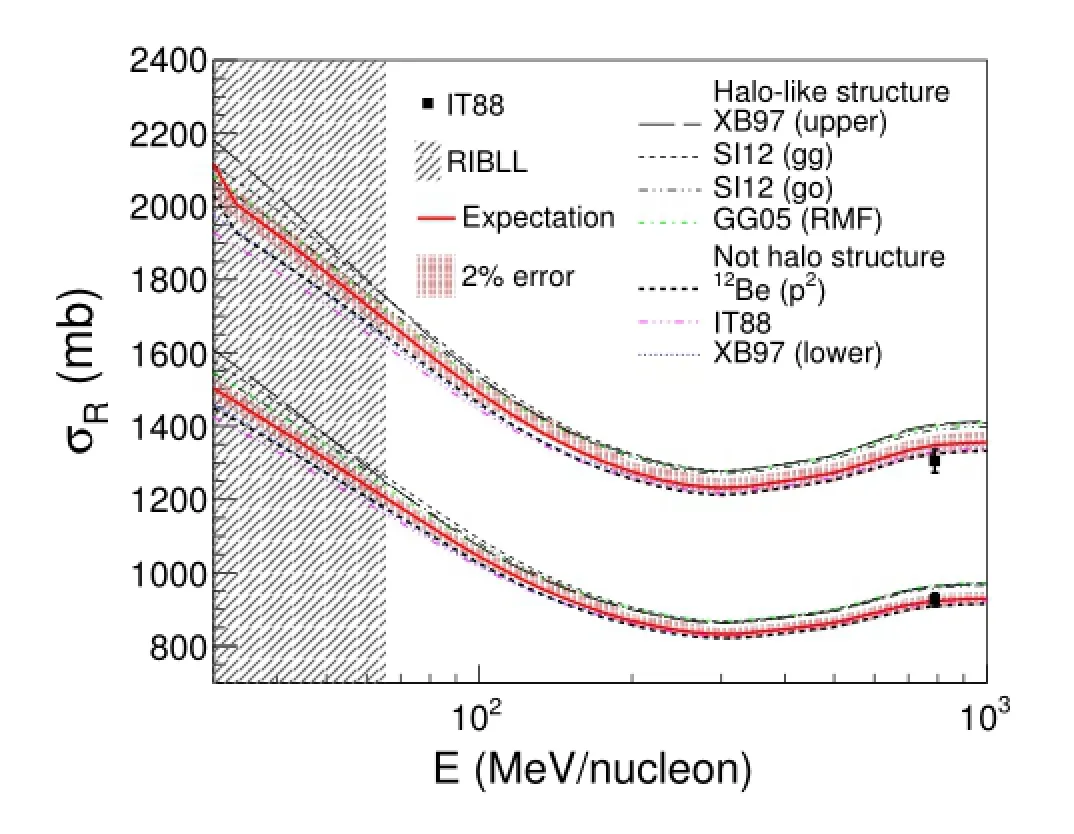
Fig.2.(Color online)The calculations ofσR(E)corresponds to current nuclear-matter density distributions of12Be(XB97:[41], SI12:[33],GG05:[42],IT88:[30]).The upper group of lines corresponds to theσRof12Be+Al,and the lower group of lines corresponds to theσRof12Be+C.
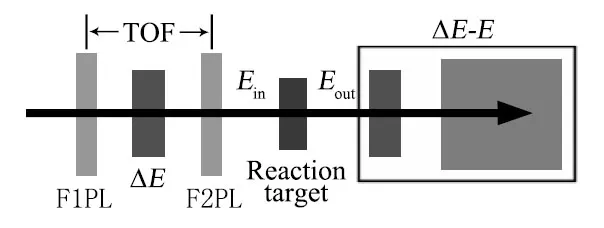
Fig.3.Schematic diagram of typical experimental setup.
Besides the detection system,the target material and thicknesstandincidentenergyofthe12BebeamEinshallbedetermined before the experiment.Regarding the target material,12C is a good candidate,because its nuclear-matter density distribution is well determined and its mass number is comparable with12Be,so itsσRis more sensitive to the12Be surface structure.Another target,27Al,is also needed for reducing the target-dependence of the result.
For thetandEin,there are direct impact factors,such as the transmission rateR,12Be outgoing energyEoutafter the reaction target,and energy pointEmeanwith certain restriction for each of these factors,hence it is diff i cult to considertandEinseparately.We studied the relations between these parameters through calculations,which includes:
(1)Eoutfor certainEinandt,Eoutwas calculated by LISE++[43];
(2)Emeancould be determined through(Ein+Eout)/2 ap-proximately;
(3)σR(Emean)was calculated using MOL[FM]based on the nuclear-matter density distribution of the expectation in Fig.1;
(4)Ris calculated by Eq.(1)with certaintand correspondingσR(Emean).
Then,the trends ofRvarying withEinunder differenttandEoutwere obtained.Fig.4 shows the calculation results of12Be+C.Each dash line corresponds to the samet,each dash dot line corresponds to the sameEout.Subsequently,we took into account the restrictions ofR,EoutandEmeanto give propertandEin.As mentioned before,Emeanshould be less than 50MeV/n to ensure the physical goal,andEout(viz.the energy of12Be right before the ΔEdetector)should be above 20MeV/n to ensure the availability of ΔE−Emethod.
Ris restricted by systematic error if the statistical error is small enough.It is of certain diff i culty to achieve 0.1% systematic error for a directly measured quantity,likeR.To ensure a<2.5%precision ofσR,the factor 1/lnRbefore the systematic error ofRin Eq.(5)shall be less than 25.AccordinglyRshould be less than 0.96.Therefore,proper ranges oftandEinare indicated as the hatched area in Fig.4.
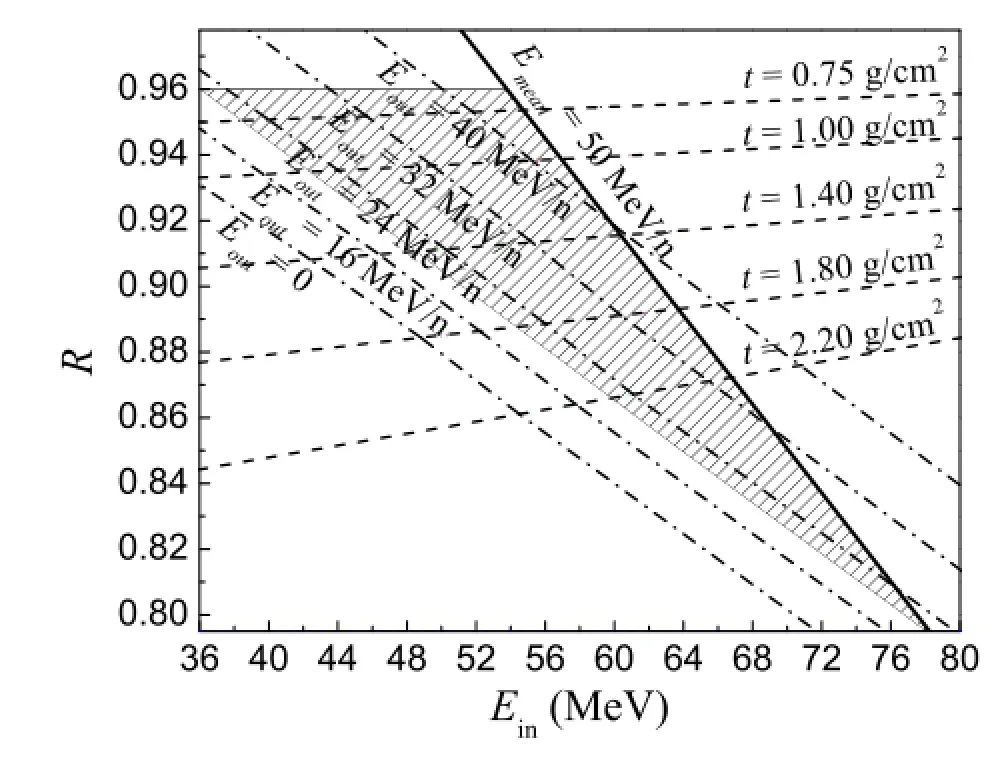
Fig.4.The change trends ofRwithEinunder differenttandEout.
In the energy region of 30–50MeV/nucleon we intend to obtain three data points by using subtraction method.As shown by Conditions(1)and(2)in Fig.5,at incident beam energy ofE1andE2,with target thickness oft1andt2,reaction cross sectionsσ1andσ2are measured by the transmission method,respectively,and by adjustingE1andE2,both the outgoing beam energiesEoutcan be of the same energy. Then,the reaction rate in the target in Condition(2)shall be equal to that of the corresponding thickness oft2in the target in Condition(1).By subtracting the two data,one obtains anotherσRas,
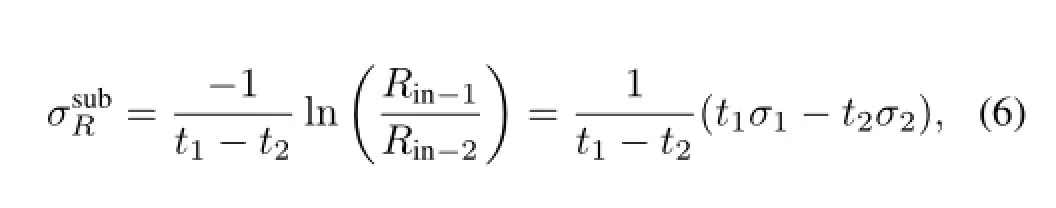
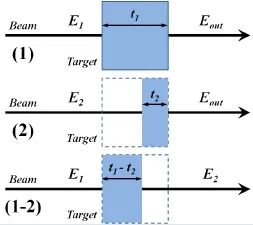
Fig.5.(Color online)Schematic diagram of the subtraction method.
whereRin−1andRin−2denote the transmission rates of the target-in experiment in Conditions(1)and(2),respectively. The transmission rates of the target-out experiments do not appear in Eq.(6)because the reaction rate outside the target is canceled between the two measurements.The error of this deducedσRwas determined in Ref.[40].Through this method,three data points can be obtained with only two measurements.This greatly improves the eff i ciency of the experiment.The key point is that the outgoing energiesEoutin the two measurements should be the same.And the interval between the two adjacent incident beam energiesEinshould be over 15MeV/nucleon in order to make sure the energy points are evenly distributed between 30–50MeV/nucleon.
Thus we have decided the range atEin,and C and Al target thicknesses,and the detecting system.Next,we are to determine the number of events we need according to the requirement of the statistical error,and estimate the requisite beam intensity.
According to Eq.(3)the statistical error should be less than 0.5%,so that it will not be a main error source,which gives
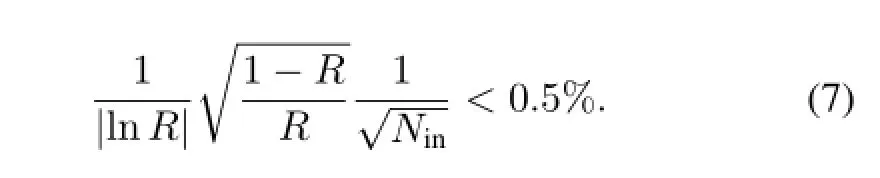
SinceRis at most 0.96,Ninof 106is already suff i cient.So, it will take only 103seconds of beam time under typical condition of 103s−1beam intensity,which is very practical.
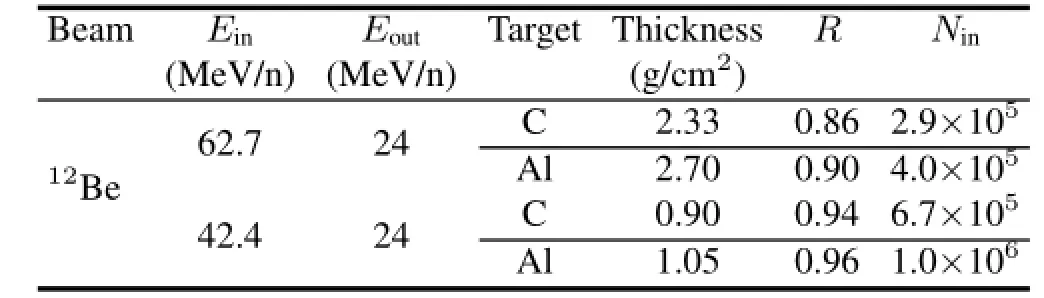
TABLE 1.Experimental scheme
To sum up,for the experiment a12Be beam of about 103s−1intensity at 20–70MeV/nucleon is needed to provide the projectile particles,and the outgoing energy of12Be after the reaction targets in the two measurements should be the same.In addition,a Si and a scintillator detector areneeded for particle identif i cation.Finally,we select two energy points,f i nd the corresponding target thickness,evaluate theRand decide corresponding requirement ofNin.The detailed experimental scheme is given in Table 1.
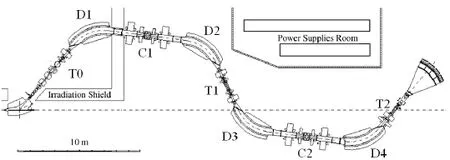
Fig.6.Schematic diagram of the layout of RIBLL.
Wef i ndthattheRadioactiveIonBeamLinein Lanzhou(RIBLL)[44]is a suitable candidate for providing12Be beam.The schematic diagram of the layout of RIBLL is shown in Fig.6.
The primary beam18O8+is accelerated by the Heavy Ion Research Facility of Lanzhou(HIRFL)and introduced to RIBLL.It bombards the production target of Be at T0 and generates the secondary beam of12Be.An Al degrader at C1 is used for an energy-loss analysis of the secondary beam separation.Another Al degrader at T1 is used for energy degradation.Two slits at C1 and C2 is used for momentum acceptance controlling.Two plastic scintillation counters at focal points T1 and T2 can provide the TOF information.Si solid state detector(SSD)at T2 can be used to provide the ΔEsignals for particle identif i cation before the reaction target.EnergyEinof the incident beam right before the reaction target isdeterminedbytheBρvalueofthefourthdipolemagnetD4. Based on this conf i guration,the12Be beam condition is simulated by LISE++using a typical 100enA primary beam of18O8+at 80MeV/nucleon.Major parameters of the simulation result given in Table 2.It’s worth mentioning that similar experiments have been performed on RIBLL since 2000[45–49].From their results we infer that typically the error ofσRis up to about 5%including 3%–4%systematic error.So we need further consideration based on the real performance of RIBLL to reduce the error especially the systematic error.
For the detecting system,typically a Si detectors of 1500µm thickness is competent for the ΔEmeasurement, and a CsI(Tl)scintillator detector of 30mm thickness is adequate for theEmeasurement.It should be noted that the Si detector is made of single crystal,hence the concern of channeling effect to the particles being detected.By tilting the Si detector against the beam axis at a certain angle,the fraction of channeling events can be reduced to<1%[40].The tilting angle can be determined by studying the angle dependence of the channeling events in advance.
Based on the above feasibility study,theσRmeasurement is reasonable and valid,and the requisite conditions can be satisf i ed.Through the measurement the nuclear-matter den-sity distribution of12Be ground state can be determined and then used to extract the component of12Be ground state.In Sec.IV,we elaborate that how to determine thesorbital component throughσR.
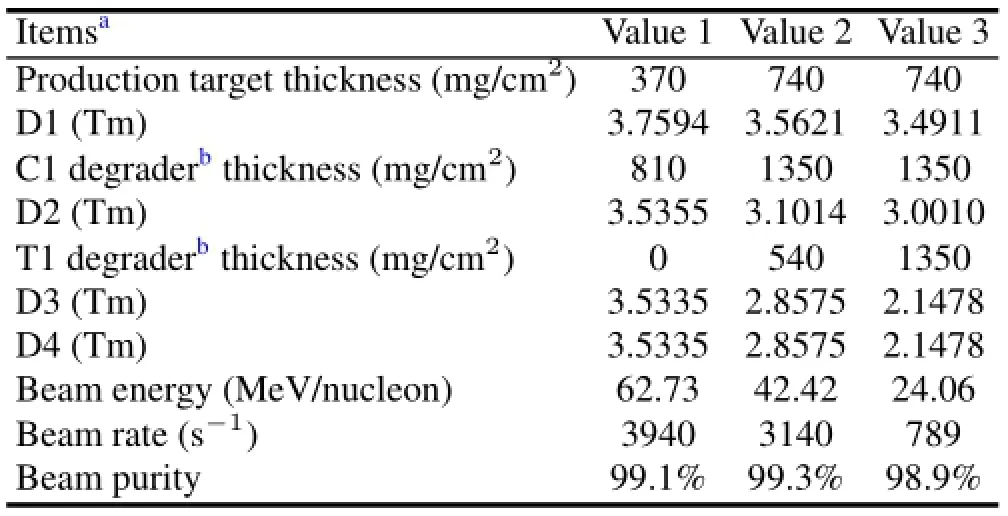
TABLE 2.Major parameters of12Be beam condition at RIBLL
IV.EXTRACTION OF THEsORBITAL COMPONENT OF12BE GROUND STATE
As shown by the fermionic molecular dynamics(FMD) calculations(see the inset(b)in Fig.10 of Ref.[33]),different conf i guration mixings of the two valence neutrons in12Be lead to different nuclear-matter density distributions of12Be,and the difference is obviously indicated in the surface structure of12Be.Inspired by this result,we bring forward a method to extract the ground state component of12Be.
In the method,we treat12Be as a system of10Be core plus two valence neutrons as usual.The10Be determines the nuclear-matter density distribution of the core part of12Be, while the two valence neutrons determine the outer part density distribution.According to the intruder conf i guration of12Be[4],the two valence neutrons are populated in 1p1/2, 1d5/2and 2s1/2states at certain occupation probabilities.So we can construct the outer structure of12Be according to a certain conf i guration as long as a model can give preferable density distribution of the two valence neutrons correspond-ing to different states.By using an appropriate function to describe the core structure of12Be,we can construct a nuclearmatter density distribution of the ground state of12Be.By adjusting the proportion of the components,we can f i nd a nuclear-matter density distribution which is consistent with the experimental result.Then the corresponding proportion can provide conf i guration information of12Be ground state.
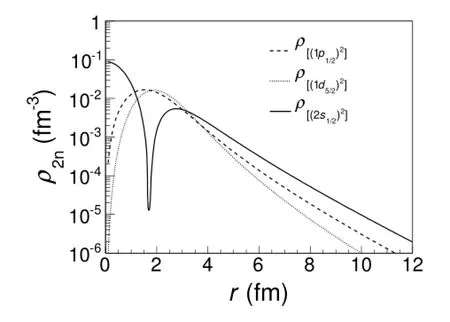
Fig.7.Density distributions of the two valence neutrons corresponding to 1p1/2,1d5/2and 2s1/2states.
We have tried to extract the ground state component of12Be in order to verify the feasibility of the method.As mentioned above,a precondition of the method is to obtain the valence neutron density distributions corresponding to 1p1/2, 1d5/2and 2s1/2states.Usually single particle model(SPM), three-body-model,cluster model,shell model,etc.are used to calculate the density distribution of the valence neutron.In this article,the SPM[35]is used.In this SPM,the Woods-Saxon potential,the Coulomb barrier and the centrifugal barrier are taken into account.The nuclear part of the potential assumed is written as
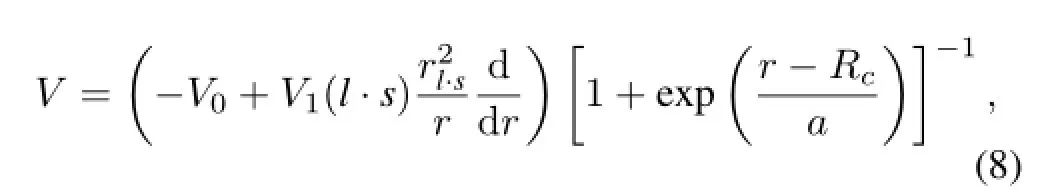
whereV0is the depth of the Woods-Saxon potential,V1= 17MeV is thel·sstrength taken from Ref.[50],rl·s=1.1fm is the radius of spin-orbit potential,Rc=r0A1/3(r0= 1.2fm)is the radius of the Woods-Saxon potential,anda= 0.6fm is the diffuseness parameter.V0is adjusted to reproduce the separation energy of the valence neutron.Here we treat the two valence neutrons as equal and set the separation energy of single valence neutron to be a half of the two-neutron separation energy of12Be.The corresponding nuclear-matter density distributions of the two valence neutrons are shown in Fig.7.We can see that the 2s1/2state has larger density in the surface.Although different models will not give exactly the same density distributions of the two valence neutrons,we infer that our result is less modeldependant based on the fact thatsintruder valence neutron conf i guration is the chief cause of the halo-like structure in light nuclei just as the cases of11Li and11Be.
Then we consider a conf i guration mixing of 1p1/2,1d5/2and 2s1/2for the two valence neutrons as follows:

whereαandβdenote the occupation probability of(1p1/2)2and(1d5/2)2conf i guration,respectively.The integrals of the single conf i guration density and mixed density are all normalized to be two nucleons.Combining the10Be core distribution of Gaussian-Gaussian(GG)parametrzation given in Ref.[33],we calculated the correspondingσRand obtained a range ofσRaccordingly,as indicated in Fig.8.We can see clearly that theσRis sensitive to thesorbital occupancy, and it is diff i cult to derive thepanddorbital occupancies from theσRdata.This is because the 2s1/2component contributes much more to the surface structure of12Be than the other components.By using theσIof12Be on C in Ref.[30], we extract the upper limit of thesorbital occupation probability to be about 56%.The upper limits are indicated by the vertical line in Fig.8(c).
The result indicates that thesorbital is not a dominant component in12Be ground state.It is supposed to be the reason why the halo-like structure in12Be is not evident,because thesorbital component is the major contribution to the halo-like structure.Compared with the calculations given by Ref.[4,20–22,24],ourresultisrelativelysmall(Table3).Although our result is consistent with theβdecay result given by Ref.[42],large uncertainty exists in both results.Therefore,higher precision extraction is needed.
By comparing the increasing trend ofσRin insets(c)and (f)of Fig.8,one can sees that at low energy region,σRis even more sensitive to thesorbital occupancy.This implies that the extraction uncertainty can be reduced ifσRat low energy region is used.So,we calculateσRbased on ansorbital occupation of 28%(half the value of the upper limit)and aporbital occupation probability of 25%,as the percentage of 1p1/2component was determined as 25±5%[10].The result is shown in Fig.8(f),in which the hatched area indicates 2%error band.Thereby we can extracted that uncertainty of thesorbital occupation probability is about 23%.And take into account that six data points will be available from the experiment introduced in previous section,the precision of the extractedsorbital occupation probability is expected to be around 9%.This makes the experimental measurement ofσRat low energy region more desirable.
Since the percentage of the 1p1/2component has been determined by Gamow-Teller transition strengths[10],if either 1d5/2or 2s1/2component is extracted precisely,the ground state conf i guration of12Be shall be reliably determined.Our method provides a promising approach to extract the 2s1/2component of12Be ground state and to determine the ground state conf i guration of12Be.Through the proposedσRmeasurements,we expect to extract thesorbital occupation probability with 9%uncertainty.
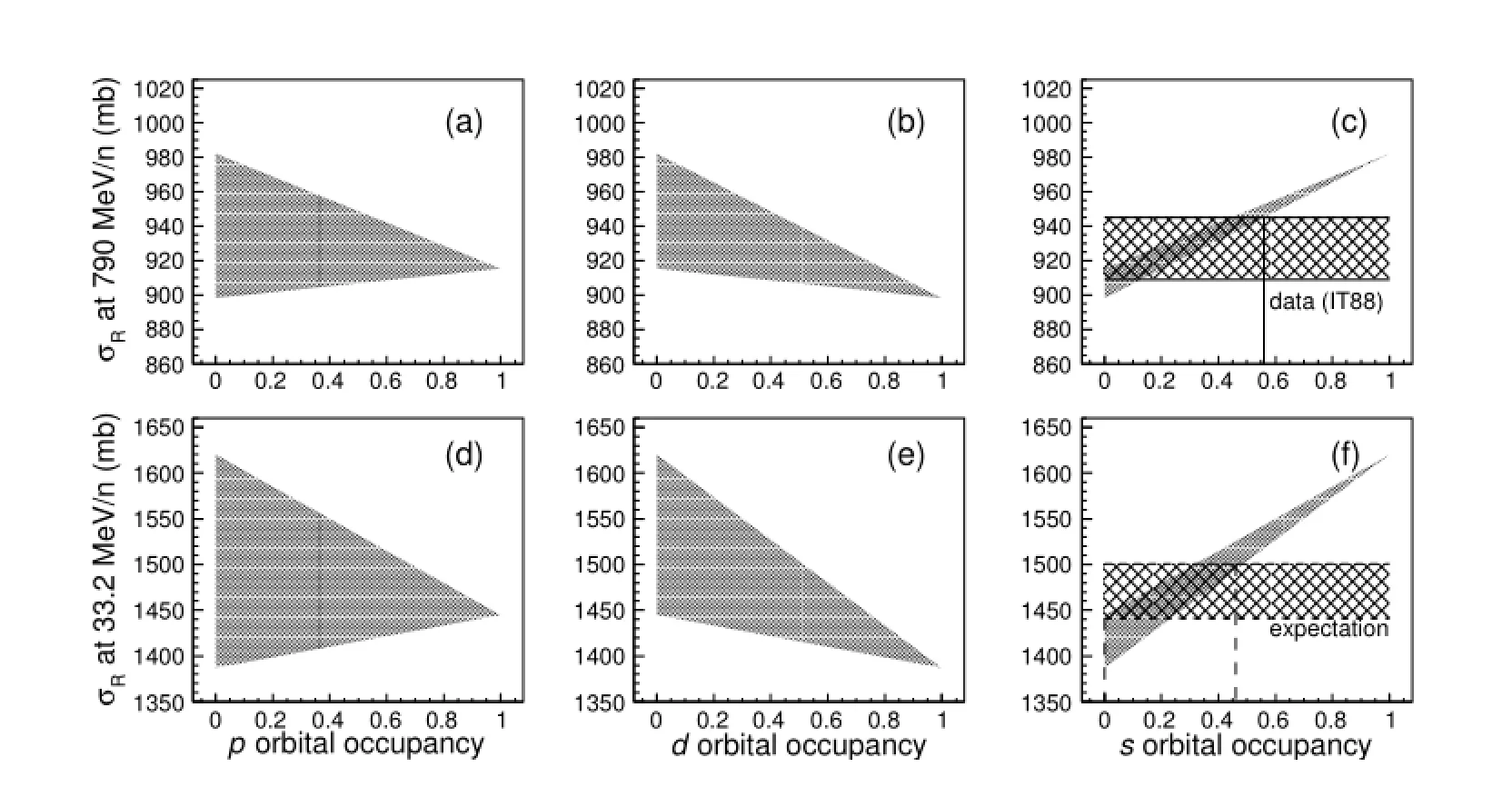
Fig.8.The reaction cross section(σR)of12Becalculated at 33.2MeV/nucleon and 790MeV/nucleon,plotted against the occupation probability of the valence neutrons conf i guration inp,dandsorbit.

TABLE 3.Two-neutron occupancy(%)for12Be(g.s.)as10Be+2n.
V.SUMMARY
In summary,the ground state structure of12Be is of great signif i cance.The ambiguity of the conf i guration of12Be ground state has attracted our attention.We bring forward to determine thesorbital component of12Be ground state by measuring theσRof12Be on C and Al at several tens of MeV/nucleon.By using existed interaction cross section data of12Be on C at 790 MeV/nucleon,we roughly determine the upper limit of thesorbital occupation probability of12Be ground state to be 56%with SPM calculations.The precision of thesorbital occupation probability is expected to be 9% by using the proposed 2%σRdata.The feasibility of theσRmeasurement is carefully studied and concrete procedures of the experiment are given.
ACKNOWLEDGEMENTS
We wish to thank Dr.Mitsunori Fukuda and his group in Osaka university for their precious help.
[1]Tanihata I,Hamagaki H,Hashimoto O,et al.Phys Rev Lett, 1985,55:2676–2679.
[2]Freer M.Rep Prog Phys,2007,70:2149–2210.
[3]Kanungo R,Gallant A T,Uchida M,et al.Phys Lett B,2010,682:391–395.
[4]Navin A,Anthony D W,Aumann T,et al.Phys Rev Lett,2000,85:266–269.
[5]Ren Z Z and Xu G O.Phys Lett B,1990,252:311–313.
[6]Ren Z Z.J Phys G,1994,20:1185–1194.
[7]Ren Z Z,Xu G O,Chen B Q,et al.Phys Lett B,1995,351: 11–17.
[8]Ren Z Z,Mittig M,Chen B Q,et al.Phys Rev C,1995,52: R1764–R1767.
[9]Pain S D,Catford W N,Orr N A,et al.Phys Rev Lett,2006,96:032502.
[10]Meharchand R,Zegers R G T,Brown B A,et al.Phys Rev Lett, 2012,108:122501.
[11]Zahar M,Belbot M,Kolata J J,et al.Phys Rev C,1993,48: R1484–R1487.
[12]Audi G,Wapstra A H,Thibault C.Nucl Phys A,2003,729: 337–676.
[13]Kanada-En’yo Y and Horiuchi H.Progress of Theoretical Physics Supplement,2001.142(Copyright(c)Progress of Theoretical Physics 2001 All rights reserved.):pp.205.
[14]KorsheninnikovAA,AleksandrovDV,AoiN,etal.NuclPhys A,1995,588:c23–c28.
[15]Freer M,Anglique J C,Axelsson L,et al.Phys Rev Lett,1999,82:1383–1386.
[16]Kanada-En’yo Y and Horiuchi H.Phys Rev C,2003,68: 014319.
[17]Ito M,Itagaki N,Sakurai H.Phys Rev Lett,2008,100:182502.
[18]Dufour M,Descouvemont P,Nowacki F.Nucl Phys A,2010,836:242–255.
[19]Blanchon G,Vinh Mau N,Bonaccorso A,et al.Phys Rev C, 2010,82:034313.
[20]Barker F C.J Phys G,1976,2:L45–L47.
[21]Fortune H T and Sherr R.Phys Rev C,2006,74:024301.
[22]Barker F C.J Phys G,2009,36:038001.
[23]Fortune H T and Sherr R,J Phys G,2009,36:038002.
[24]Romero-Redondo C,Garrido E,Fedorov D V,et al.Phys Rev C,2008,77:054313.
[25]Glauber R J.Lectures in Theoretical Physics,Interscience, New York 1959,Vol.1,pp.315.
[26]Ma Y G,Shen W Q,Feng J,et al.Phys Lett B,1988,302: 386–389.
[27]Ma Y G,Shen W Q,Feng J,et al.Phys Rev C,1993,48:850–856.
[28]Kox S,Gamp A,Perrin C,et al.Phys Rev C,1987,35:1678–1691.
[29]Shen W Q,Wang B,Feng J,et al.Nucl Phys A,1989,491: 130–146.
[30]TanihataI,KobayashiT,YamakawaO,etal.PhysLettB,1988,206:592–596.
[31]Liatard E,Bruandet J F,Glasser F,et al.Europhys Lett,1990,13:401.
[32]Warner R E,McKinnon M H,Needleman J S.Phys Rev C, 2001,64:044611.
[33]Ilieva S,Aksouh F,Alkhazov G D,et al.Nucl Phys A,2012,875:8–28.
[34]Takechi M,Fukuda M,Mihara M,et al.Phys Rev C,2009,79: R061601.
[35]Tanaka K,Yamaguchi T,Suzuki T,et al.Phys Rev Lett,2010,104:062701.
[36]Tanaka K,Fukuda M,Mihara M,et al.Phys Rev C,2010,82: 044309.
[37]Fan G W,Ph.D.thesis,Shanghai Institute of Applied Physics, Chinese Academy of Sciences,2012.
[38]Takechi M,Fukuda M,Mihara M,et al.Eur Phys J A,2005,25:217–219.
[39]Ahlen S P.Phys Rev A,1978,17:1236–1239.
[40]Takechi M.Elucidation of the behavior of reaction cross sections at intermediate energies and halo structure of 6He.PhD Theis,Osaka University,2006,34–77.
[41]Bai X,Hu J.Phys Rev C,1997,56:1410–1417.
[42]Gangopadhyay G,Roy S.J Phys G Nucl Partic,2005,31: 1111–1122.
[43]Tarasov O B and Bazin D.Nucl Phys A,2004,746:411–414.
[44]Sun Z,Zhan W L,Guo Z Y.Nucl Instrum Meth A,2003,503: 496–503.
[45]Fang D Q,Shen W Q,Feng J,et al.Phys Rev C,2000,61: 064311.
[46]Fang D Q,Shen W Q,Feng J,et al.Eur Phys J A,2001,12: 335–339.
[47]Cai X Z,Zhang H Y,Shen W Q,et al.Phys Rev C,2002,65: 024610.
[48]Zhang H Y,Shen W Q,Ren Z Z,et al.Nucl Phys A,2002,707: 303–324.
[49]Ozawa A,Cai Y Z,Chen Z Q,et al.Nucl Instrum Meth B, 2006,247:155–160.
[50]Bohr A and Mottelson B R,Nuclear Structure,Vol.I(Benjamin,New York,1975).
[51]Thompson I J and Zhukov M V.Phys Rev C,1996,53:708–714.
[52]Robertson R G H.Atomic Masses and Fundamental Constants 5,Springer,1976,pp.147–153.
[53]KellerH,AnneR,BazinD,etal.ZPhysA-HadronNucl,1994,348:61–62.
[54]Suzuki T and Otsuko T.Phys Rev C,1997,56:847–856.
[55]Barker F C.Phys Rev C,1999,59:535–538.
10.13538/j.1001-8042/nst.25.020501
(Received January 10,2014;accepted in revised form March 10,2014;published online March 20,2014)
∗Supported by the National Natural Science Foundation of China(No. 11179018 and 11305238)and the Instrument Developing Project of the Chinese Academy of Sciences(No.YZ201246)
†Corresponding author,caixiaolu@sinap.ac.cn
 Nuclear Science and Techniques2014年2期
Nuclear Science and Techniques2014年2期
- Nuclear Science and Techniques的其它文章
- A hybrid voxel sampling method for constructing Rad-HUMAN phantom∗
- Measurement of keffwith an improved neutron source multiplication method based on numerical analysis∗
- Simulation of neutron diffusion and transient analysis of MSR∗
- Ordered water monolayer on ionic model substrates studied by molecular dynamics simulations∗
- Demonstration of Pm-147 GaN betavoltaic cells
- Upgrade to the front-end electronics of the BESIII muon identif i cation system
