一种高性能时钟晶体振荡器电路设计
鲍钰文,徐 瑶
(湖北大学材料学院,湖北武汉 430062)
晶体振荡器具有稳定的谐振特性和较高的品质因数Q,因此其谐振特性既精确又稳定,被广泛应用于彩电、计算机、遥控器等各类振荡电路中,以及通信系统中用于频率发生器、为数据处理设备产生时钟信号和为特定系统提供基准信号[1-3]。目前所用的时钟芯片大都采用32.768 kHz晶振,为系统提供稳定的32.768 kHz初始振荡频率。但晶体振荡属于机械谐振,其需要合理的设计谐振电路与晶体配合。Pierce晶体振荡器其结构简单,便于集成,故得到了广泛应用。小型化、低功耗、高精度始终是此类芯片的发展研究方向。但传统的Pierce电路结构存在输出振幅受电源电压变化影响、功耗偏大、且输出频率受寄生效应影响等缺点。针对上述不足,本文设计了改进方案:(1)增加振幅控制电路,降低振荡输出波形的幅度,提高振幅的稳定性,同时降低电路的功耗。(2)增加频率校正电路,可使芯片的输出频率得到精确校准,消除晶振固有参数变化和芯片封装管脚的寄生电容对输出频率的影响,在具有温度检测功能的系统中还可实现输出频率的温度补偿,最终实现振荡电路的低功耗与高精度的频率输出。且采用该设计还可获得高性能的时钟日历芯片。
1 晶振与Pierce晶体振荡器
晶片振荡是基于其压电效应,其等效电路图如图1中所示。石英晶体的等效电路由静态电容C0,串联等效电感LS、串联等效电容CS、串联损耗电阻RS组成。从石英晶体的等效电路可知,其有两个谐振频率,一个串联谐振频率fS,一个并联谐振频率fP,只有在频率fS和fP之间石英晶体成感性,为晶体的振荡带[4]。本文仿真选取32.768 kHz石英晶体等效模型参数为:C0=1.3 pF,LS=8 kH,CS=2.95 fF,RS=30 kΩ,可计算得到

该模型的振荡带宽为fP-fS=37.1 Hz,精度满足仿真要求。
图1中Pierce电路是该电路的典型结构。电路以反相放大器作为增益元件,在反相器的输入与输出之间跨接一个负反馈电阻RF,该电阻一方面给反相器提供直流偏置,稳定反向放大器的静态工作点;另一方面,起振之后构成负反馈,减小反相放大器的增益,稳定振幅。其电阻阻值必须足够大从而增加频率的稳定性和降低振荡电路的功耗。图中RF约为100 MΩ,为减小芯片的面积,设计采用MOS管实现[5]。C1与C2构成晶振的负载电容,Q为石英晶体。
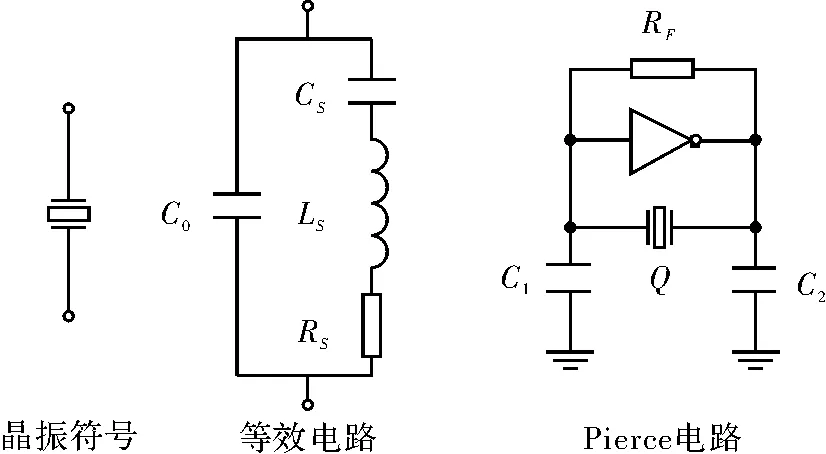
图1 晶振与Pierce振荡电路
2 改进后的Pierce振荡器
传统的Pierce振荡器结构简单,输出波形振幅大,导致振荡电路功耗较大,输出频率也受石英晶体的出厂频率以及芯片PAD电容和PCB上布线寄生电容等的影响,芯片工作时实际输出频率与理想频率(32.768 kHz)之间存在一定的频率偏差,因此在对功耗和频率精度要求严格的时钟芯片设计应用中受到限制。针对以上不足,本文对传统的Pierce结构进行了改进:(1)增加振幅控制电路;(2)增加频率校准电路。改进后的电路结构由频率校准模块、反相放大模块、振幅控制模块、启动电路模块4部分组成,其设计电路如图2所示。
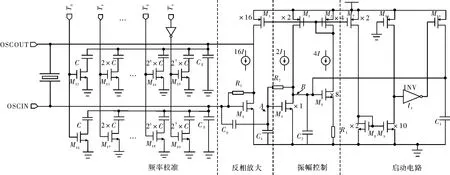
图2 改进后的振荡电路
2.1 频率校准的原理与电路设计
晶体振荡电路的实际输出频率与晶体的固有串联谐振频率之间存在一定的频率牵引量,为,其中,ω是实际输出频率;ωs是晶振的固有串联谐振频率。频率牵引量与负载电容关系如式(3)所示[6-7]

式(3)中,C0是晶振的静态电容;Cs是晶振的固有串联谐振电容;C1、C2是晶振两端的电容,其串联值称为晶振的负载电容。当出厂频率与理想频率之间存在一定偏离时,可通过校正晶振的负载电容,得到精确的输出频率。
频率校准实现电路如图2中频率校准部分。T7~T0为内部8位校正寄存器的存储值,通过I2C接口写入。当输入信号 T6~T0是高电平时,控制相应的NMOS管导通,使晶振负载电容增大。而当T7是高电平时,NMOS15、NMOS19截止,使负载电容减小,所以B7为负载电容调整的符号位。当芯片通电时,上电复位信号使校正寄存器复位,T7~T0输出均为0,因此晶振两端的电容初始值为CX+27C,其变化范围分别为[CX,CX+(28-1)C]。
2.2 振幅控制原理与电路设计
若振荡器的输出振幅较大,不仅显著增大了振荡电路的功耗,还会降低晶振的寿命。振幅控制电路的设计原理是:电路检测振荡输出的振幅,反馈确定反向放大器的偏置电流,振荡输出振幅大于设定值时,振幅控制电路降低反向放大器的偏置电流,反之,增大反向放大器的偏置电流。电路在上电时,振荡输出振幅为0,使反向放大器具有大的偏置电流,有利于起振。其电路如图2中振幅控制模块所示。M1、M2、M4、M5和R1构成与电源电压无关的偏置电流源,M1和M2的宽长比比值为 1∶2,M4,M5的宽长比的比值为 1∶8。为降低功耗,设计使偏置电流源中的MOS管工作在亚阈值区,设流过 M1管的电流为2I,可得到[8]
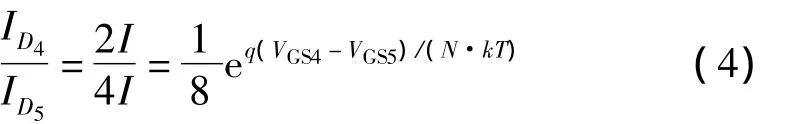
其中,ID4、ID5分别为流过 M4,M5的电流,N 为亚阈值斜率参数。将VGS4-VGS5=4I×R1,代入等式(4)中可得,该偏置电流与电源无关,通过选取适当的R1值,便可设置所需的偏置电流。设计取电流I≈8 nA,确保电路具有较低的功耗。
图2中电阻R2跨接在M4栅漏两端,MOS管的栅端无电流,因此M4栅漏间的直流电压相等。若漏电流保持不变,M4栅极上的平均电压应保持不变。当振荡器开始工作后,振荡输出的信号经电容C0隔直通交后,传递M4的栅极。当振幅增大时,若要保持恒定的偏置电流不变,M4栅极直流电压必定下降,因此M5的栅极电压也必定随着振幅增大而下降,从而使偏置电流I减小。反向放大器的偏置电流由电流源M3确定,大小为16I,因而当振荡器的输出振幅振荡增大时,系统降低反向放大器的偏置电流,以到达稳定振幅、减小功耗的目的。
2.3 反向放大电路模块与启动电路模块的设计
改进后的电路结构还包含反向放大电路模块和启动电路模块。反相放大电路采用恒流偏置共源放大器,由M3提供恒流偏置,M6为共源放大管,R3为负反馈电阻。恒流偏置电流的大小为16I,受振幅控制电路调制。
启动电路模块,保证电路上电后能正常启动。在直流偏置未建立时,M9输出电流为0,M10导通使反相器I1输出低电平,PMOS管M11导通,给电容C3充电,使B点电压升高,从而M2,M5导通,保证偏置电流可正常建立。当直流偏置建立后,M9通过镜像产生10I的电流,M10管的栅长值L过大,使反向器I1输出变为高电平,关断M11,电路完成启动。
3 电路仿真结果及讨论
3.1 晶体振荡电路环路增益与相位仿真
仿真采用0.5 μm-5 V CMOS工艺模型,仿真温度设定25℃,仿真工具是Spectre。图3是设计的晶体振荡电路环路增益与相位仿真结果,电源电压分别设定为3 V和1.1 V,晶体负载电容为6 pF的条件下,从仿真图中可看出,在频率为32.7681 kHz处,环路增益为5.2855,相位为0,在该频率处满足振荡的条件。当电压下降到1.1 V时,同样在频率为32.7681 kHz处,环路增益为3.8330,相位为0,也满足振荡条件。这表明其可在1.1 V电压下正常振荡,电路具有较宽的工作电压范围。
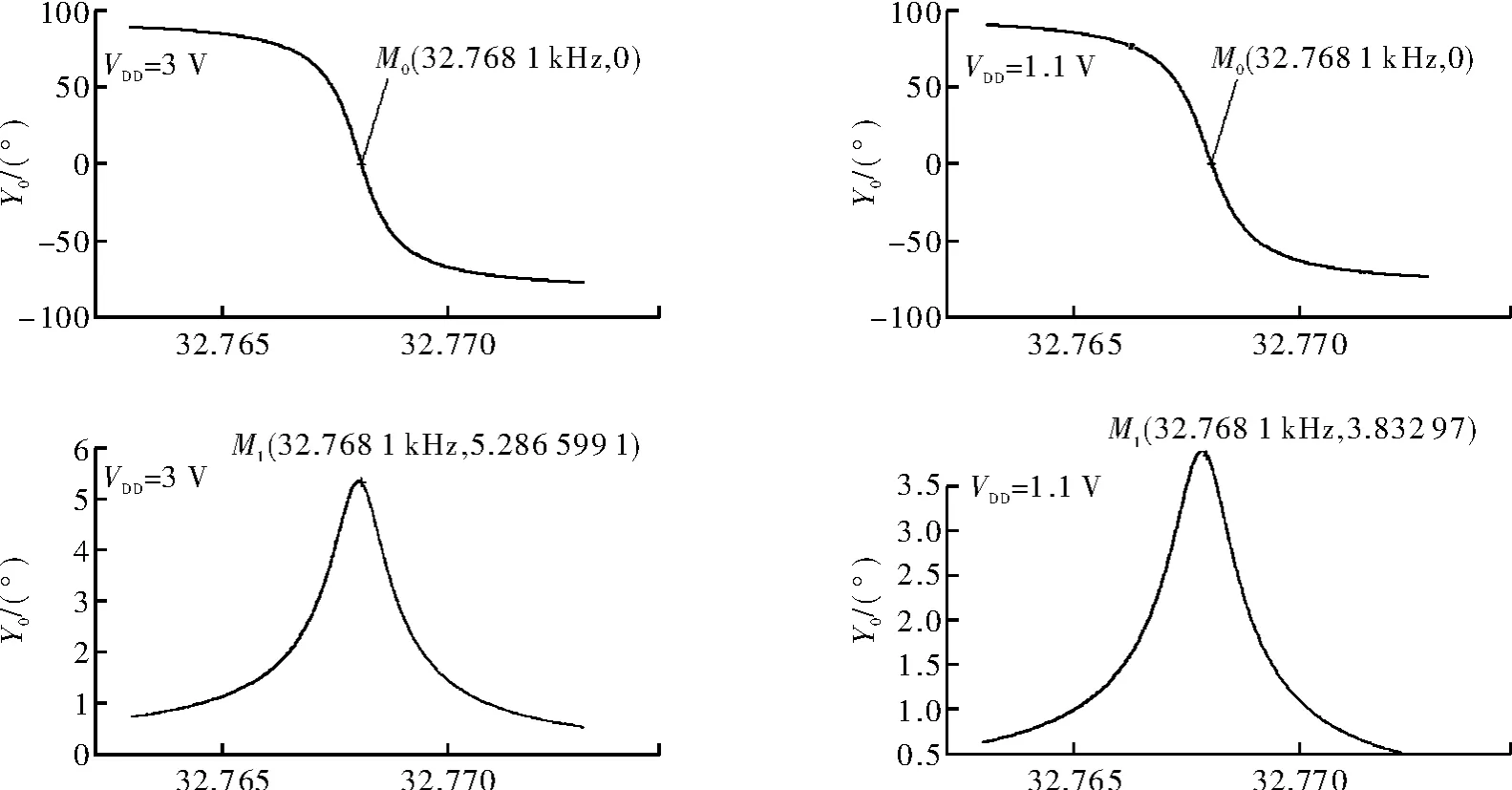
图3 晶体振荡电路环路增益与相位仿真
3.2 晶体振荡电路瞬态仿真
图4和图5均为电源电压为3 V时,振荡电路的瞬态仿真结果,其分别反映了振荡电路的输出波形以及电路消耗的电流。从图中可看出,振幅控制的过程:在起振初期振幅较小时,电路消耗较大的电流,随着振幅的增大,振幅控制电路调控偏置电流,使电路消耗的电流降低。当电路稳定后,电流最终消耗值约为130 nA,振荡电路输出波形峰峰值为367.2 mV。电路消耗极低的功耗,且起振时间<1 s。

图4 振荡电路输出波形

图5 振荡电路消耗电流
3.3 频率校准仿真
图6为频率校准范围的仿真图,设计取 Cx=4.4 pF,C=62 fF。调整校正寄存器的存储值,使晶体振荡器的负载电容分别为最大值、初始值和最小值。仿真得到满足起振条件的初始频率为32.7681 kHz,频率校准范围为(32.7658 kHz,32.7779 kHz),校准的平均精度为1.44 ppm。通过校准电路可获得高精度的输出频率。

图6 频率校准范围
4 结束语
高精度使得时钟芯片的市场前景广阔。本文对传统Pierce振荡器结构进行了改进,反向放大器采用恒流源供电,增加振幅控制及频率校准电路。仿真结果表明,新结构的电路具有低功耗、高输出频率精度和宽工作电压范围等优点。
[1] 龚美霞.石英晶体元器件技术的发展及应用[J].国外电子元器件,2001(1):9-11.
[2] 彭正宏,刘三清,邹雪城.一种高稳定性的32.768kHz晶体振荡器的谐振电路的设计[J].计算机与数字工程,2004,32(1):73 -75.
[3] 邹望辉,应建华,雷鉴铭.用于实时时钟的高性能晶体振荡器[J].计算机与数字工程,2004,32(6):78 -81.
[4] 童诗白,华成英.模拟电子技术基础[M].北京:高等教育出版社,2004.
[5] 刘惩,李冰.用于时钟芯片的Pierce晶体振荡器设计[J].半导体技术,2008,33(1):30 -34.
[6] VITTOZ E A,DEGRAUWE M G R,BITZ S.High - performance crystal oscillator circuits:theory and application[J].Solid - State Circuits,IEEE,1988,23(3):774 -783
[7] BRENDEL R,CHIROUF F,GILLET D.Quartz crystal oscillator classification by dipolar analysis[C].Alushta,Crimea:Advanced Optoelectronics and Lasers, IEEE, 2003:233-243.
[8] JACOB B R,HARRY W L,DAVID E B.CMOS circuit design,layout,and simulation[M].Newyork:Willey - IEEE Press,2010.

