设施直线型自动布置的算法之二

常双领（北京物资学院 信息学院，北京 101149）

0 引 言

企业要对物流成本进行有效的控制，需要对生产设施进行优化布置。一方面要求尽可能的减少移动次数，缩短移动距离。另一方面要尽可能地避免回退现象，回退现象的发生与设施布置有密切关系。优良的设施布置可以使物流费用至少减少10%～30%[1]。设施布置常见的形式有直线型，L型、U型、O型，其中直线型是最简单也是最常见的形式。设施直线型最优布置问题是一个具有重要应用价值但至今仍然未解决的理论问题[2]，因为m个产品n个设施的不同布置方案共有n!，完全列举这些布置显然不可取。对这类问题的求解通常采用“从至表”试验法，这种试验法一般都需要用经验来进行调整和改进。有的学者也对这种“从至表”试验方法做了一些改进[3]，但实际效果并不理想，可操作性也不强。有的学者也提出了一些新的“从至表”优化模式和新的准则[2]，有的学者提出了在“从至表”基础上提出了十字形分析法等[4]。有的学者给出用遗传算法进行一些自动布置的方法[5]。有的学者根据设施之间的紧密程度进行排序，以确定在车间布置中的优先位置并赋予不同的权重[6]，一般学者都没有考虑回退惩罚下的优化布置方法。本文对这种直线型布置问题做了研究，给出了一种自动布置算法。首先，从零件工艺路线图开始自动生成初始从至表。其次，通过对从至表进行变形计算，得到一个优化的布置方案以及对应的从至表和物流费用。文中的算法是基于Matlab语言描述的，程序是通过Matlab函数给出的，生成的从至表是以矩阵的形式表示的，也称为从至表矩阵。

1 算法描述

以例1为研究背景，给出m个产品n个设施自动布置的算法

例1：4个产品，8个设施的零件工艺线路图如图1所示，产品A，B，C，D的当量物流量分别是2，3，1，1。

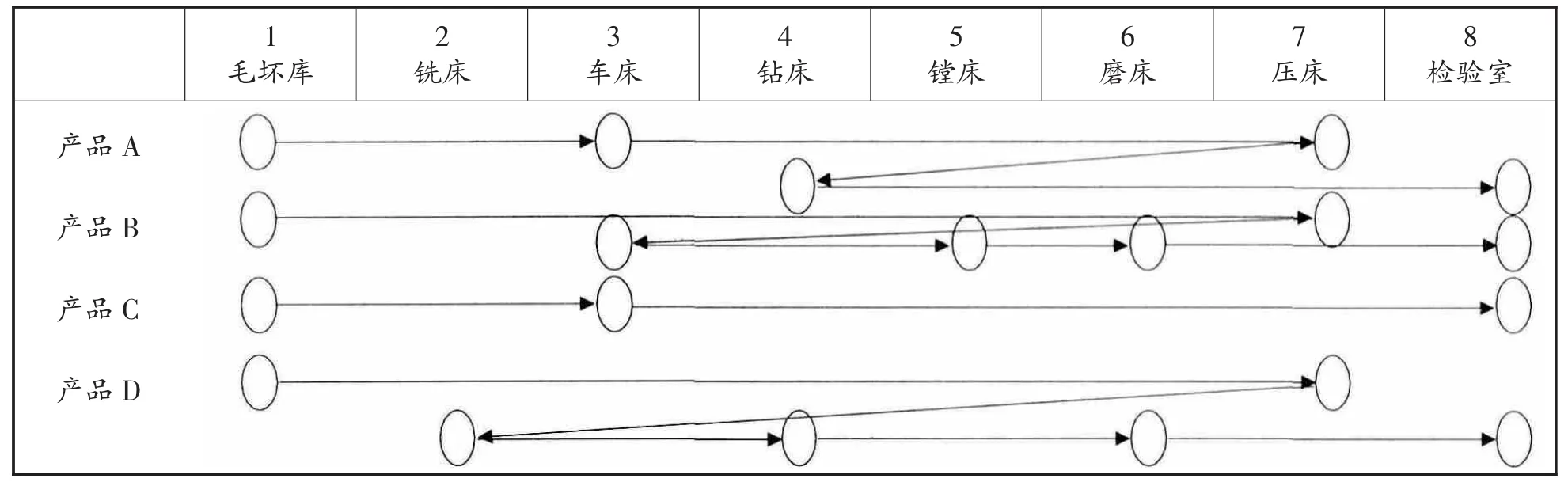
图1 产品工艺路线图

算法1：（由产品工艺路线图生成从至表）

（1）把m个产品n个设施的产品工艺图转化为一个m行n列的工艺路线矩阵a；

（2）构造n个零件的当量物流量为向量b；

（3）初始化从至表c=zeros（n）；

（4）for i=1∶m，for j=1∶n；

（5）if a（i,j＋1）＞0，u=a（i,j），v=a（i,j＋1），c（u,v）=c（u,v）＋b（i），结束，否则（4）；

（6）结束。

算法1的实现：通过[c]=fromto（a,b）函数实现。

函数输入参数说明：a为工艺路线矩阵，即a的第i行，为第i个产品的工艺路线，b为零件的当量物流量向量，即b（i）表示第i个零件的当量物流量。

函数功能：输入a,b返回物流从至表矩阵c。

构造产品的当量物流量的向量为b=（2,3,1,）1。

（2）在Matlab窗口中输入[c]=formto（a,b），则在Matlab窗口中输出的结果为：

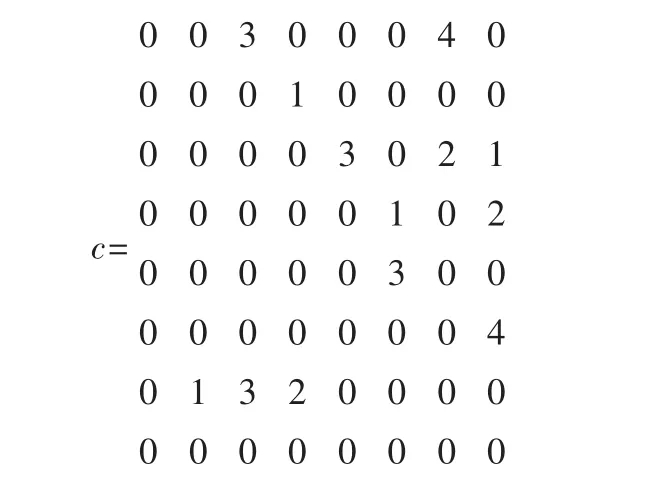
设施以1-2-3-4-5-6-7-8方式排列的从至表如矩阵c所示。

算法2：（对初始从至表矩阵进行行列变换，得到一个优化的布置）

（1）给出初始从至表矩阵c（c为n×n矩阵），c对应的布置记为p=（1,2, …,n）称为初始布置，计算初始布置的物流费用w0。令w（1）=w0＋1；w（2）=w0；k=1。

（2）while w（k＋1）＜w（k）。

（3）将从至表矩阵中的第一行（列）分别与第二，第三，…，第n行（列）交换，得到n-1个从至表矩阵，每一个从至表矩阵对应一种布置，在n-1种布置中找到物流费用最小的一种布置，最小的物流费用记w，如果w＜w0，则把物流费用最小的布置做为新的布置p，对应的矩阵做为新的从至表矩阵c，并且令w0=w；否则布置和从至表矩阵均保持不变。

（4）将从至表矩阵中的第二行（列）分别与第三，第四，…，第n行（列）交换，得到n-2个从至表矩阵，每一个从至表矩阵对应一种布置，在n-2种布置中找到物流费用最小的一种布置，最小的物流费用记w，如果w＜w0，则把物流费用最小的布置做为新的布置p，对应的矩阵做为新的从至表矩阵c，并且令w0=w；否则布置和从至表矩阵均保持不变。这样依次下去。

（5）最后将从至表矩阵c中的第n-1行（列）与第n行（列）交换，计算物流费用，记为w，如果w＜w0，则把物流费用最小的布置做为新的布置p，令w0=w，对应的矩阵做为新的从至表矩阵c；否则布置和从至表矩阵均保持不变。从而得到第一阶段的一个优化布置方案。

（6）令k=k＋1；w（k＋1）=w0。返回（2）。

（7）结束。

算法2的实现：通过[p,m,w]=mincost（c,x）函数实现：

函数输入参数说明：c为初始从至表矩阵（c为一个n×n的矩阵），x为惩罚倍数（当x=1是不进行回退惩罚，当x＞1是进行回退惩罚）。

函数功能：输入c,x，输出设施的布置以及对应从至表矩阵和物流费用，分别返回给p,m,w。

如例1：在Matlab窗口中输入：[p,m,w]=mincost（c,1），则在Matlab窗口中输出的结果为：

即设施的布置为1-7-3-2-5-4-6-8，从至表如矩阵m所示，物流费用为53。

2 数值实验与结果分析

例2：（见文献[3]中的例2）原始从至表如表1。

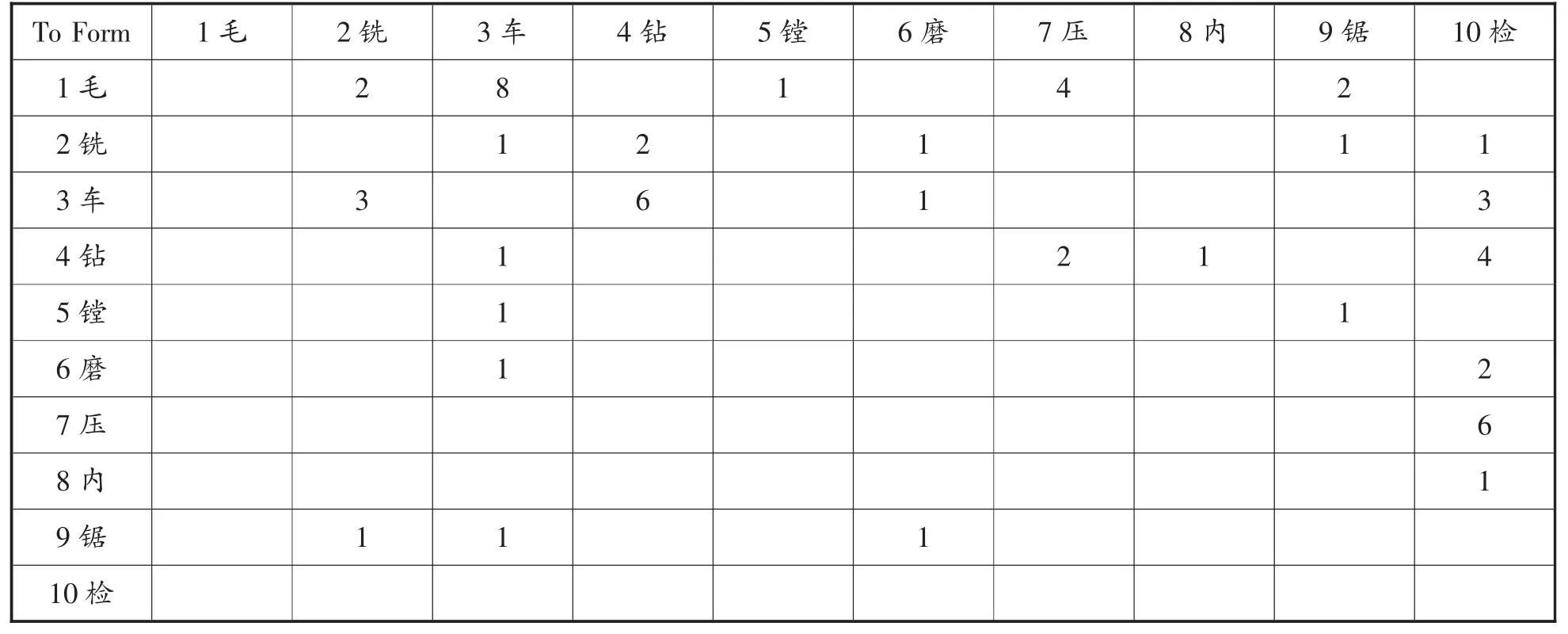
表1 从至表

（2）在Matlab窗口中输入：[p,m,w]=mincost（c,1），则在Matlab窗口中输出的结果为：

即设施的布置为5-9-2-1-3-4-7-10-6-8，从至表如矩阵m所示，物流费用为119。

结果分析：初始布置1-2-3-4-5-6-7-8-9-10的物流费用为207，经过优化布置后的物流费用为119。而文献[3]优化的物流费用为133。

如果在例2中对回退进行2倍惩罚时：

在Matlab窗口中输入：[p,m,w]=mincost（c,2），则在Matlab窗口中输出的结果为：

3 结束语

这种方法实现了从产品工艺路线图开始，设施进行直线型布置的自动化，数值实验的结果表明这种算法是十分有效的。

[1]蔡临宁.物流系统规划——建模及实例分析[M].北京：机械工业出版社，2003:60-124.

[2]王俊峰，李兹强.设备组单行布置问题的“从至表”法优化模式与新准则探索[J].合肥工业大学学报（自然科学版），2005,28(9):1163-1166.

[3]贾春玉，崔剑.设备单行布置从至表试验法的改进[J].工业工程与管理，2008(1):127-130.

[4]谢健.生产车间设备布置的“从至表”优化法[C]//决策科学的力量方法与应用.北京：卓越出版社，2001:1-80.

[5]S.G.Ponnambalam,V.Rankumar.A Genetic Algorithm for the Design of a Single-Row Layout in Automated Manufacturing Systems[J].The international Journal of Advanced Manufacturing Technology，2001(18):512-519.

[6]张毕西，刘永清.多对象生产单元设备双行布置优化分析[J].华南理工大学学报（自然科学板），1999,5(27):45-51.