金属粉末轧制的力学模型及数值模拟研究

刘明俊,刘白

（深圳信息职业技术学院 机电工程学院，广东 深圳 518172）

【博士论坛】

金属粉末轧制的力学模型及数值模拟研究

刘明俊,刘白

（深圳信息职业技术学院 机电工程学院，广东 深圳 518172）

金属粉末轧制工艺能够生产一般工艺难于或无法生产且成分精确、性能优良的板带材，是制取高性能以及特殊用途材料的粉末冶金成形工艺。在粉末轧制工艺的力学行为研究中，传统的数学模型被证明所提供的作用有限，基于有限元方法的数值模拟为此提供了一种灵活高效的途径。基于把粉末体看作是可压缩连续体的假设，根据椭球面屈服准则推导了金属粉末体变形的弹塑性本构关系。采用了合适的本构关系积分算法，并对摩擦模型进行了分析。基于MSC.Marc平台的二次开发工具编制了相关的用户子程序，对铁基粉末的轧制过程进行了三维弹塑性有限元数值模拟。该程序的准确性已在对粉末闭模压制的数值模拟及实验对比中得到了验证。此外，分析了轧制速度、摩擦系数等对轧制力和相对密度分布的影响。

粉末轧制;有限元方法;本构关系;椭球面屈服准则

金属粉末轧制是粉末冶金中一种非常重要的成形工艺，通过在两个反向旋转的轧辊中将初始松散的粉末体轧制成具有一定密度及强度的带材。粉末轧制出来的带材组分和密度均匀，性能优良，因此在高新材料及特殊功能材料的制取中具有独特的优势，在工艺、装置及力学模型方面有很多研究[1-3]。

由于粉末轧制中力学性能的复杂性，更准确的研究应该考虑轧制速度、轧辊直径、辊缝大小以及摩擦等多种因素对带坯的综合影响，但是力能参数的确定和优化通常难于采用传统的试错法准确实现，况且试错法并不具有通用性。力能参数的确定对指导工艺优化以及轧制设备的研发具有决定性意义，有必要采用力学模型等定量化的手段进行分析。当前可用于计算粉末轧制力能参数的解析模型主要有Johanson模型、主应力法、能量法等[4]。其中主应力法由Katashinskii首次应用于粉末轧制的计算[5]。Bindhumadhavan在药剂粉末轧制中对Johanson 模型做了实验验证[6]。Dec则在其粉末轧制研究中比较了Johanson 模型及主应力法的应用[7]。解析力学模型被证明在轧制力能参数的计算方面作用有限。根据他们的研究，在特定条件下，利用这两种方法对咬入角、轧制力、轧制力矩及某些参数的计算可以获得较理想的结果。然而随着条件的复杂化，解析模型的作用明显有限，误差将不断放大。主要原因在于，考虑到计算的可行性，解析模型对计算条件作出太多的简化。

数值模拟为粉末成形工艺力能参数的研究提供了一种高效的手段，也可以为粉末成形工艺优化及成形专用设备的研制提供有用的参考。借助于有限元方法，可以在计算中引入复杂的力学模型及边界条件，并且在计算中可以方便地获得工艺参数。在粉末成形数值模拟领域，目前，被广泛接受的一种假设是把金属粉体系统看作为“可压缩连续体”，这样可以借助连续体塑性力学来研究粉末体的变形特性。相关地，可以应用的材料屈服准则一个是由Von Mises准则引申而来的椭球面屈服准则，该屈服准则在主应力空间中展示为一个椭球体表面[8,9](图1 (a)).另一种是用于岩土类材料的屈服准则，如Cam-Clay 模型，Drucker-Prager 帽盖模型等[10,11]。

图1 两种屈服模型Fig.1 Two kinds of yield models

虽然粉末压制成形工艺的数值模拟已经开展多时，但是在粉末轧制成形方面，研究并不多见，尤其在金属粉末轧制方面更少见。Dec利用Drucker-Prager帽盖模型对微晶纤维素的轧制过程进行了研究，并利用ABAQUS软件做了数值模拟[7]，分析了摩擦及进给应力对轧制力、咬入角等工艺参数的影响。

相对而言，椭球面屈服准则在应用过程中所需的参数更容易获得，因此，本文采用该准则对铁基粉末的轧制成形进行数值模拟研究，文中计算基于MSC.Marc平台所做的二次开发子程序展开。

1 数值模型

1.1 屈服准则

结合金属粉体的变形特性，可以把金属粉体看作为可压缩连续体，借助连续体塑性力学研究金属粉末成形的力学特性并进行有限元数值模拟研究。对于可压缩连续体，其屈服准则反映为变形过程中从弹性变形到塑性变形的一种临界状态。相关的椭球面屈服准则通常可用下式表示[8]：

式中

A,B及δ—跟粉末基体材料属性及相对密度ρ相关的参数;

Y0—对应于基体致密材料的屈服极限.

Kuhn及Doraivelu在提出该屈服准则时，假设当表观总变形能达到某一临界值时，材料开始屈服[8,9]。根据他们的研究，A、B参数可以表达为：

1.2 本构关系

根据椭球面屈服模型（1），可以得出粉体材料的弹塑性本构关系。式（1）可以表示为如下函数形式：

对式（3）求偏导，得到：

在关联流动法则中有以下定义

通过式（4）及式（5），可以得出应力-应变关系：

式中

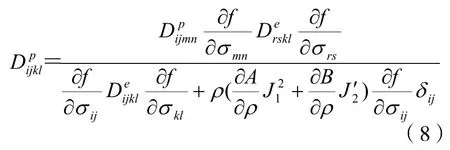
在数值计算中，本构关系合理的积分算法对于弹塑性求解计算中的收敛性和精度非常重要。本文将采用欧拉算法，对一般的非线性问题求解，该算法是合适的。基于此，求解中各增量步的应力表示如下：

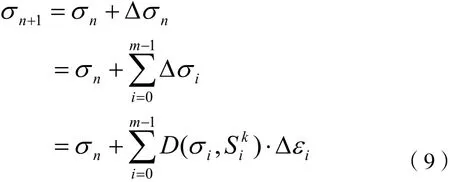
式中

1.3 模型参数

对于数值计算而言，除了本构关系之外，还需要确定跟材料相关的参数，在此主要有、弹性模量及泊松比。根据式（1），为跟相对密度相关的参数。根据文献[12]中的研究，该参数可以选用如下形式：

式中

cρ—对应屈服应力为0时粉体的临界相对密度。

根据Kuhn的实验[10]，变形过程中的泊松比υ为跟相对密度相关的函数，即：

同样，变形过程中的杨氏模量跟相对密度也相关：

式中：

E0 —致密基体材料的杨氏模量。

1.4 摩擦模型

在成形过程及其数值计算中，摩擦是一个相当复杂的元素，跟法向应力、相对速度及接触界面的其他因素都密切相关。在粉末轧制中，摩擦力是驱动成形过程得以顺利进行的主导因素，摩擦模型描述准确与否对数值计算的准确性非常重要。

MSC.Marc中提供的摩擦模型有剪切模型，库仑模型等。对金属粉末轧制来说，剪切模型是一个更合理的描述，本文计算采用了这种模型。剪切模型假设摩擦力为变形区域中等效应力的函数，即：

式中

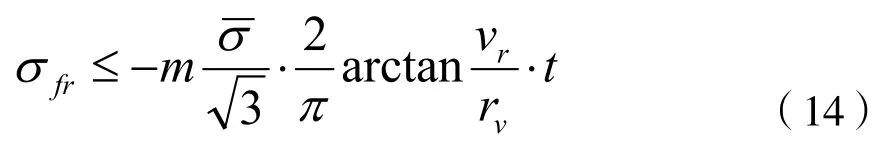
2 粉末轧制过程的有限元分析

以上确定了数值计算相关的力学模型及相关的材料参数，结合这些因素，本文基于MSC.Marc的二次开发接口开发了计算子程序。根据以上的模型，需要在计算子程序中输入的材料参数有杨氏模量、初始相对密度以及基体材料的屈服极限。

2.1 用户程序的验证

为了验证计算模型及用户程序，首先对一个立方体粉体模型的压制过程进行了模拟[12]。压制前松装粉体的尺寸为10×10×19.65 mm，最大压制力70 KN。三维计算模型包含1024个六面体全积分单元。基本材料参数为：E0=210 GPa，Y0=205 MPa，。

图2 对立方体压制计算获得的相对密度分布Fig.2 Density distribution of a cubic sample by simulation

计算所得的相对密度及压制曲线分别如图2、图3所示。由图2可知，压制后的立方体其密度分布为两端高、中间低，上边高、下边低，这些现象是由于压制过程中摩擦因素使然，跟实际的压制结果相符。同时根据图3中压制曲线的模拟及实验结果的对比，本文所述的力学模型及计算程序在用于粉末成型的模拟计算中，能够获得可供参考的可靠结果。

图3 压制过程载荷(N)-位移(mm)曲线Fig.3 Curve of load-displacement of the punch

2.2 粉末轧制计算结果

基于以上计算，本文进一步对粉末轧制过程进行数值模拟。通常地，竖直方式的粉末轧制方式如图4所示。

图4 粉末轧制示意图Fig.4 Schematic of the rolling compaction

图中H表示进给方位侧粉体的厚度，h为辊缝，B为辊面宽度，D为辊径，为带材厚度，v为轧制速度。本文计算中，进给厚度为5mm，辊面宽度为50mm。辊缝h为2.0mm，辊径D为100mm。有限元计算模型包含了2000个六面体全积分单元，同时假定辊面为刚性表面，即轧辊本身没有变形。计算采用前述压制模拟中的材料参数。

整个轧制计算过程分成两个步骤，在第一步中将轧辊辊缝放大，随后两辊相向移动，压缩至所需要的辊缝，与此同时压缩粉体模型。随后在第二步中轧辊开始转动进行轧制，带动轧件进入稳定轧制阶段。事实表明，这种咬入处理方式跟实际情况更加接近。

计算分析了轧制速度、轧辊摩擦系数对轧制力及相对密度分布的影响。图5、图6分别为在不同的轧制速度及摩擦系数下计算所得到的轧制力。图7、图8则为在不同的轧制速度及摩擦系数下计算所得到的沿轧制方向的相对密度分布。

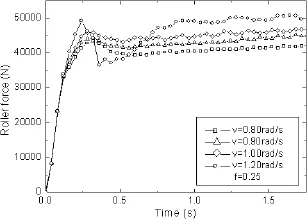
图5 轧制力随轧制速度的变化结果Fig.5 Roller force as a function of roller velocity

图6 轧制力随摩擦系数的变化结果Fig.6 Roller force as a function of friction coefficient

图7 相对密度随轧制速度的变化结果Fig.7 Relative density along the rolling direction obtained in different rolling velocity

图8 相对密度随摩擦系数的变化结果Fig.8 Relative density along the rolling direction obtained in different friction coefficients

根据图5、图6的计算结果表明，轧制力随着轧制速度及摩擦系数的增加而增加。在轧制过程的压下及开始轧制过渡阶段，轧制力有所波动，当进入稳态轧制后，轧制力也开始进入稳定状态。这种现象跟致密材料的轧制过程也是类似的。图7、图8的计算结果表明，相对密度随着摩擦系数的增加有所增加，但当轧制进入稳定状态后，这种趋势并不明显。而随着轧制速度的增加，相对密度则反而有所降低。本文的计算同时表明，相较于摩擦系数，轧制速度对轧制力及相对密度的分布有着更明显的影响。

3 结论

本文基于把粉末体看作是可压缩连续体的假设，根据椭球面屈服准则分析了金属粉末体变形的弹塑性本构关系。采用了合适的本构关系积分算法，并对摩擦模型进行了分析。基于MSC.Marc平台的二次开发工具编制了相关的用户子程序，对铁基粉末的轧制过程进行了三维弹塑性有限元数值模拟。综合分析了轧制速度、摩擦系数等对轧制力和相对密度分布的影响。根据这些影响关系，可以通过调节成形参数来获得特定密度、强度及其他性能的轧制带材。

在粉末轧制过程中，同时存在材料非线性及几何非线性问题，因此，更准确地，应该在计算模型中增加几何非线性的因素。同时在模拟过程中，网格模型的高度变形也是影响计算的一个重要因素。因此，更准确地，应该在计算过程中考虑以上因素，在模型中添加几何非线性因素，并采用自适应网格划分，这些因素都在本文作者的研究之中，以期获得更综合的分析结果。

（References）

[1]Deevi S C.Powder processing of FeAl sheets by roll compaction[J].Intermetallics,2000,8 (5-6):679-685.

[2]Hirohata T,Masaki S,Shima S.Experiment on metal powder compaction by differential speed rolling[J].J Mater Process Technol,2001,111 (1-3):113-117.

[3]Jiang Y,He Y H,Tang Y W,et al.Fabrication of Ti-Al alloy sheets by element powder cold roll forming and reactive synthesis[J].Zhongguo Youse Jinshu Xuebao,2004,14 (9):1501-1507.

[4]Johanson J R.A rolling theory for granular solids[J].J Appl Mech Trans ASME,1965,32:842-848.

[5]Katashinskii V P,Stern M B.Stress-strain state of powder being rolled in the densification zone:I.Mathematical model of rolling in the densification zone[J].Sov Powder Metall Met Ceram,1983,22 (11):17-21.

[6]Bindhumadhavan G,Seville J P K,Adams M J,et al.Roll compaction of a pharmaceutical excipient:experimental validation of rolling theory for granular solids[J].Chem Eng Sci,2005,60 (14):3891-3897.

[7]Dec R T,Zavaliangos A,Cunningham J.Comparison of various modeling methods for analysis of powder compaction in roller press[J].Powder Technol,2003,130 (1-3):265-271.

[8]Kuhn H A,Downey C L.Deformation characteristics and plasticity theory of sintered powder materials[J].Int J Powder Met,1971,7 (1):15-25.

[9]Doraivelu S M,Gegel H L,Gunasekera J S,et al.A new yield function for compressible P/M materials[J].Int J Mech Sci,1984,26:527-535.

[10]Tran D V,Lewis R W,Gethin D T,et al.Numerical modeling of powder compaction processes:displacement based finite element method[J].Powder Metall,1993,36 (4):257-263.

[11]Lewis R W,Khoei A R.A plasticity model for metal powder forming processes[J].Int J Plast,2001,17 (12):1695-1692.

[12]Chen P Q.Mechanical modeling and numerical simulation of the metal powder compaction process[D].2004,South China University of Technology,Guangzhou,China.

Mechanical models and numerical simulations on metal rolling compaction

LIU Mingjun,LIU Bai
（School of Michanical and Electrical Engineering,Shenzhen Institute of Information Technology,Shenzhen,518172,P.R.China）

In spite of its simplicity and low cost,the rolling compaction process can produce strips or plates with homogeneous and satisfactory mechanical properties.The mechanical behaviors of rolling compaction are difficult to predict accurately by traditional means.The Finite Element Method (FEM) provides an efficient approach for such problems.Based on the assumption that the powder system is a compressive continuous material,three-dimensional FEM simulations for the rolling compaction process of the iron matrix powder were proposed.The ellipsoidal yield criterion was analyzed.The correspondent elasto-plastic constitutive relationship was derived from the yield criterion.Appropriate integration algorithm and friction model were applied.The user subroutine was developed and threedimensional simulations were performed in MSC.Marc.Effects of friction coefficient and rolling velocity of the rollers on the rolling force and the distribution of the relative density were analyzed.

rolling compaction;Finite Element Method (FEM);constitutive relationship;ellipsoidal yield criterion

TF124.33

：A

1672-6332（2014）03-0071-06

（责任编辑：高潮）

2014-09-01

广东省自然科学基金面上项目（项目编号：S2012010009062）；深圳市科技计划项目（项目编号：JC201006020796A）

刘明俊（1979-），男（汉），广东兴宁人，副教授，博士。主要研究方向：计算机应用。E-mail:liumj@sziit.edu.cn