“池塘有多少桶水”与“整体思想”
江苏 蒋明玉
从前,有个国王在大臣们的陪同下,来到御花园散步。国王瞧着前面的水池,忽然心血来潮,问身边的大臣:“这水池里共有多少桶水?”众臣一听,面面相觑,谁都答不出来。国王下旨:“给你们三天时间考虑,回答出来重赏,回答不出来重罚!”随后几天里,大臣们用桶量来量去,怎么也量不出一个确切的数据。眨眼三天到了,大臣们仍一筹莫展。就在此时,一个少年走向王宫,声称自己知道池塘有多少桶水。国王命令大臣带少年去看池塘,少年却笑道:“不用看了,这个问题太容易了!”国王乐了:“哦,那你就说说吧。”少年眨了眨眼说:“这要看那是怎样的桶。如果和水池一样大,那池里就是一桶水;如果桶只有水池的一半大,那池里就有两桶水;如果桶只有水池的三分之一大,那池里就有三桶水;如果……”“行了,完全正确!”国王重赏了这个少年。
大臣们为什么不能解决国王的问题呢?原来,他们都掉进了思维定势的窠臼:一桶一桶地量。而那个少年则撇开了池塘的大小,从桶的角度思考问题,结果一下子就解决了。是的,我们在解答数学问题时,常常受条件和问题束缚,没有把握局部和整体的关系,缺乏整体思想,往往把简单的问题复杂化了。整体思想的基本特点是整体性,即把数学问题当作一个整体来思考。在数学解题中,合理运用“整体思想”,往往可以化繁为简、化难为易。下面举例来讲。
一、在计算题解答中,综观整体,从整体上把握题目,合理灵活地解题。
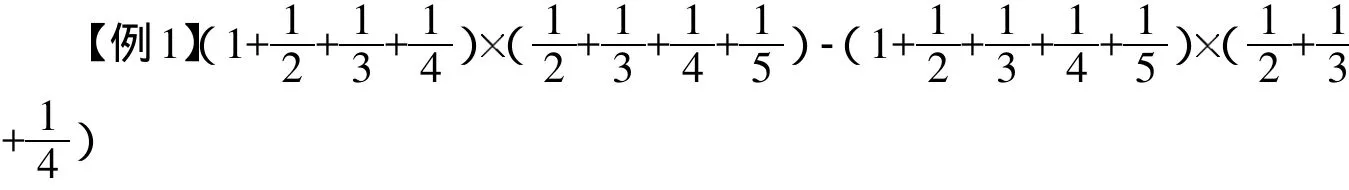
【分析与解】如果用通分的方法计算,计算将是十分烦琐。若将题目相同的和式假设为某一字母,计算就简便了。
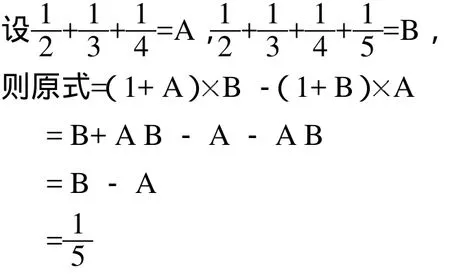
【例2】对32541这个五位数,能否改变各个数字的位置,把它变为一个五位质数。
【分析与解】许多同学的做法可能是先排除个位数2、5、4的情况,再逐步考察剩下的各种情况。其实,若从整体上把3、2、5、4、1五个数字考察一番,由于3+2+5+4+1=15,便一眼看出:无论怎样变换位置,排出来的五位数一定是“3”的倍数,而不可能是质数。
二、在面积计算题解答中,学会从整体上观察图形,进行合理转化,灵活而简洁地解答问题。
【例3】 如图1,长方形长8厘米,宽5厘米,求阴影部分的面积。
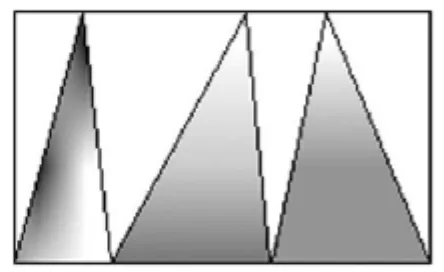
图1
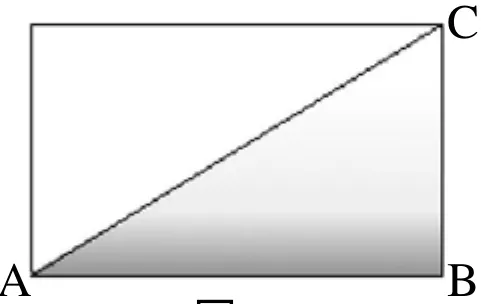
图2
【分析与解】阴影部分是由三个三角形组成的,如果分别求出三个阴影三角形的面积,就会束手无策。从整体上看图,三个三角形的高都是5厘米,而它们的底之和为8厘米,进而对图形进行转化,将三个阴影三角形转化成一个三角形(如图 2),即 S阴=S三角形ABC。
S阴=S三角形ABC=852=20(平方厘米)
三、在应用题解答中,从整体上把握数量关系,灵活而合理地解答问题。
【分析与解】“参加的人数”与“未参加的人数”前后都发生了变化,但是六年级学生的总人数是不变的。可以从“参加的人数”前后发生的变化来考虑,“原来参加的人数”是总人数的,后来又有30人参加,“这时参加的人数”是总人数的所以“30人”所对应的分率是(),因此算式是也可以从“未参加的人数”前后发生的变化来考虑,不难得出
【总结】把数学问题视作一个整体,从整体上把握问题的本质和规律,运用“整体思维”的方法解题,往往可以使解题灵活、巧妙。需要指出的是,运用了“整体思维”,并不否定“对象思维”,相反,两者要相互协调、有机统一起来。
【练一练】两个形状和大小都一样的直角三角形ABC与DEF,如下图放置,它们的面积都是2003平方厘米,而每一个三角形的顶点都恰好落在另一个直角三角形的斜边上。那么长方形ADEC的面积为( )平方厘米。