近岸海域水沙界面通量与水流挟沙力研究

郑俊，李瑞杰，于永海

（1.国家海洋局 海域管理技术重点实验室，辽宁 大连 116023；2.国家海洋环境监测中心，辽宁 大连 116023；3.河海大学 海岸灾害及防护教育部重点实验室，江苏 南京 210098）

1 引言

水沙界面通量，即近底悬沙和底沙的交换量，是近岸泥沙不平衡输运的关键问题，也是近岸泥沙运动理论研究中的难题。近岸海域的波浪、潮流以及海流等动力因素的时空尺度差异相当大，挟沙力作为计算水沙界面通量的一种方法，在考虑浪、潮、流的联合作用时存在着较大的难度。为克服上述的困难并考虑近岸动力条件的周期性，在近岸海域挟沙力的计算中，常将流速进行时间求平均处理，如半潮平均、半波平均、全潮平均、全波平均、涨潮平均以及落潮平均等。

下面列举几种目前常用的近岸挟沙力公式，对各公式的周期性动力因子的处理方法、联合作用的叠加方法及应用情况进行分析。

刘家驹［1—2］通过对连云港和天津港海域的实测资料分析得到的挟沙力公式：

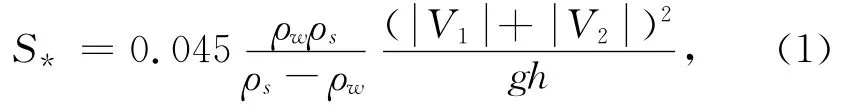
式中，S＊为挟沙力，ρs泥沙颗粒密度，ρw为水体密度，g为重力加速度，h为水深，V1为潮流时、空平均流速，V2为波浪导致的时、空平均流速，V2＝0.2为波高，C为波速。为考虑潮流和波浪的周期性作用，公式中将潮流速度取潮段平均值，波浪速度取半波长及半波周期内的平均值；为考虑波、流的联合作用，采用了潮流速度和波浪速度以各自的绝对值相加的方式，且挟沙力与叠加速度呈平方关系。该公式多被应用于淤泥质海域［3］，在实际应用时，常将系数0.045根据现场资料进行率定修正。

窦国仁和董凤舞［4］根据能量叠加原理得到的潮流和波浪共同作用下的挟沙力公式：

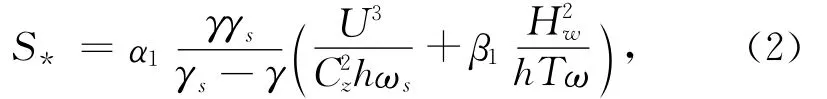
式中，γ为水体的容重，γs为泥沙颗粒的容重，α1＝0.023，β1＝0.000 4，U 为水深平均流速，Cz为谢才系数，T为波浪周期，ω为泥沙沉速。为考虑波、流的周期性，潮流速度取潮周期的平均值，波高和波周期分别取平均波高值和平均波周期值；为考虑波、流的联合作用，采用了流速三次方关系与波高平方关系相叠加的形式。该公式曾被许多学者应用于近岸海域中［5—6］。

张瑞瑾公式［7］：

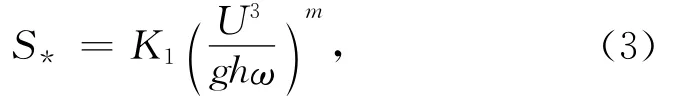
式中，K1和m为系数。该公式源自于内陆河流的研究中，也有不少学者将其在近岸海域中直接应用或改造使用［8－9］。该公式仅能计算纯流条件下的挟沙力能力，并根据不同的水流和泥沙条件对系数K1和m进行修正。

曹祖德等［10］通过边界层理论建立床面剪切力，并根据能量理论得到了波、流共同作用下的水流挟沙力公式：

式中，uw为波浪底部水质点的轨迹速度，uw＝为波速，α2和β2为系数。为考虑波、流的周期性，潮流速度取潮段平均值，波浪速度取波浪水质点的平均水平速度；为考虑波、流的联合作用，采用了潮流速度与一定比例的波浪速度进行相加的方式，并取叠加速度的三次方关系。该公式适用于淤泥质、粉沙质及沙质海域，在淤泥质条件下的计算值与刘家驹公式基本一致。

张庆河等［11］根据近岸波能耗散相关原理对窦国仁和董凤舞公式［4］中的波浪项进行了改进，提出以下公式：

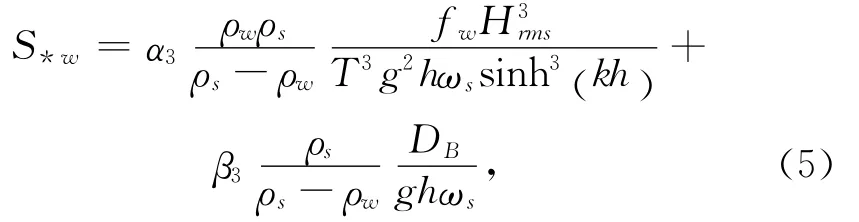
式中，S＊w为波浪引起的挟沙力，fw为摩阻因子，Hrms为波高方均根值，DB为波浪破碎引起的能量耗散，α3和β3为系数。考虑周期性时，将波高取为方均根波高值，波周期取为平均波周期。该公式适用于包括黏性及非黏性的细颗粒泥沙。

可以看出，近岸水流挟沙力的表示方法形式多样，在考虑海水运动的周期性时，水动力因子在时间平均上的方法多样，且具有不确定性，在考虑波、流共同作用时的叠加方式也不尽相同，这给近岸海域的泥沙研究及实际工程应用带来了许多的不便。本文通过平动动能叠加原理，提出了一种近岸海域多周期动力条件下联合作用的叠加方法，并结合挟沙力与切应力方法的内在联系［12］推求适用于近岸海域的水流挟沙力公式。

2 近岸动力因子

在近岸海域，浪、潮、流等动力因素的时空尺度相差很大，波浪的周期从几秒至几十秒，波长从数米至数百米；潮波的周期从半日潮的约12h至全日潮的约24人，甚至更长的分潮周期，波长约为几百千米；海流的时间尺度可达数年，甚至数十年。同时对这些因素进行综合考虑，存在着较大的难度。本文试从水体平动动能的角度出发，对近岸海域动力因子的作用进行分析，探讨一种物理意义明确、计算合理及应用简便的近岸动力因子联合叠加方法。

先考虑单频波的情况，水质点水平速度为：

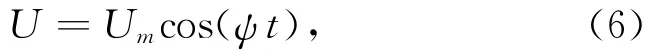
式中，U为水质点水平速度，Um为水质点水平最大速度，ψ为波动频率，t为时间。

单位质量水体的瞬时平动动能为：

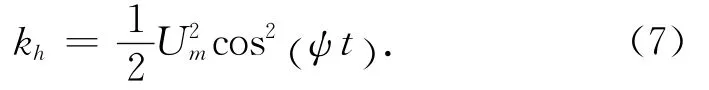
一个周期内单位质量水体的平均平动动能为：

式中，Kh为单位质量水体的周期平均平动动能，T为波周期。

提出波动有效速度Urms的概念，用以表征波动水体的平均平动动能，即

对于在一定时间间隔获取的实测数据，波动有效速度可以通过以下方法计算：

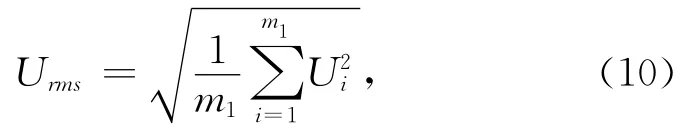
式中，m1为实测速度值的个数，Ui为实测速度值。

对于两种频率条件下的波动情况，根据动能的叠加原理，单位质量水体的周期平均平动动能为：

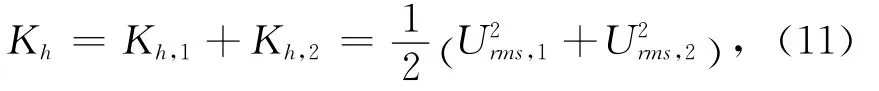
式中，Kh，1和Kh，2分别为两种频率的波动对应的平均平动动能，Urms，1和Urms，2分别为两种频率的波动对应的波动有效速度。

根据式（9）和式（11），可以进一步得到两种频率波动条件下的波动有效速度为：

式中，Urms，1和Urms，2由式（10）计算得到。

同样地，对于多种频率波动条件下的情况，波动有效速度可以通过对各频率下波动有效速度进行求均方根得到，即：

式中，Urms，j为各分频率对应的波动有效速度，m2为分频率个数。

下面分别对波浪、潮流、海流条件以及各条件相互叠加的情况进行讨论分析：

（1）波浪

根据势流理论，微幅波的水质点水平速度为：

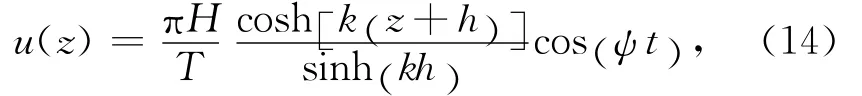
对式（14）进行垂向求平均，得到：

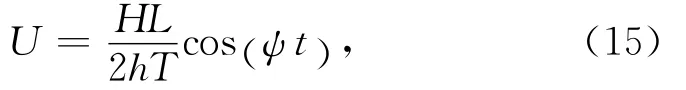
式中，L为波长。

由式（15）可知水质点的水平最大速度为：

那么，微幅波的波动有效速度为：

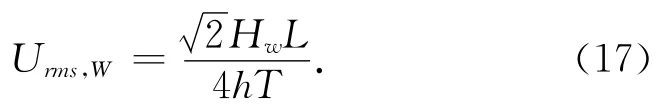
（2）潮流

潮流的有效速度可通过式（10）表示：

式中，UT，i为潮流流速，可采用实测值或模拟计算值。

（3）海流

海流是海水大规模相对稳定的流动，在较长时间内的运动速度是基本不变的，单位质量水体的平动动能可表示为：

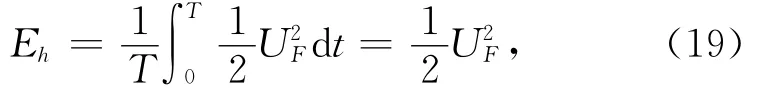
式中，UF为海流流速，T为海流周期，由于海流的长周期性，实际应用时可取有效速度为海流流速，即

在河流中，可以用该方法来考虑河流流速的有效速度。

（4）波、流叠加

将式（17）、（18）和式（20）代入式（13）中，来考虑联合浪、潮、流共同作用下的波动有效速度为：

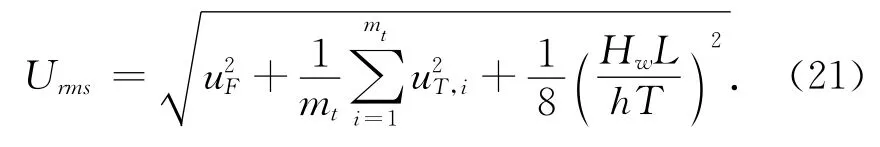
海洋波动有效速度，用以表征海水的平均平动动能，可以方便地考虑多种频率条件下的海洋周期性波动作用。悬浮泥沙随水流运动，单位质量水体的动能即为单位质量的泥沙颗粒的动能，在平衡条件下，该动能即为泥沙平衡状态时的动能，与之对应的水体含沙量即为挟沙力。下面结合海洋波动有效速度，进一步对近岸水流挟沙力进行探讨。

3 近岸挟沙力

在平衡条件下，泥沙悬浮通量等于沉降通量，即：

式中，E为悬浮通量，D为沉降通量。

沉降通量可以由下式确定：

式中，Pd为沉降概率，S为垂向平均含沙量。

悬浮通量可以表示为［13—14］：

式中，E0为冲刷系数，E0＝e0ρd，e0＝10－6m/s，ρd为底部泥沙干密度；τb为底部切应力；τc为临界冲刷切应力，为底部泥沙体积密度，d为泥沙粒径，a＝8.5×10－16m2，b＝9.07×10－3m3/kg，Γ＝0.414×103N/m3。

底部切应力由下式确定：

式中，CD为摩阻系数，，谢才系数Cz可由以下形式给出［15—16］：

由于近岸海床冲淤平衡是周期性海洋动力要素和海床长期作用的结果，为考虑海床处泥沙通量的长期的动态平衡过程，将式（22）进行时间求平均：

式中，上划线表示时间平均值。将式（23）～（26）代入式（27）中，挟沙力可表示为：

式中，Urms由式（21）通过计算得到，α＝与泥沙粒径、水深、泥沙密度等相关，临界速度当有效速度小于临界速度V0时，底部泥沙不能起动，水流挟沙力为零。对于黏性泥沙，由于絮凝作用泥沙沉速可近似取为常数，此时的系数α与泥沙沉速无关。

为了检验式（28）的适用性，并对各动力因子形式进行比较，将现场实测资料和经过验证的模拟计算结果应用于式（28）的验证。其中，实测资料采用的是浙江和福建海域的舟山、瓯江口、台州、大渔湾和三门湾海域共30个实测站位的水文、泥沙资料；模拟计算结果验证中采用的是瓯江口海域内的计算结果，包含12个断面的590组的逐时计算数据，模型验证部分见文献［14］。

验证结果如图1－图3所示，分别是挟沙力公式（28）根据波动有效速度、全潮平均速度和半潮平均速度等形式的验证情况。可以看出，采用波动有效速度的计算结果较全潮平均和半潮平均速度形式的结果更为准确。这也说明了，波动有效速度形式的动力因子能较好地反映海洋动力作用。

图1 挟沙力公式（28）采用有效速度动力因子形式的验证

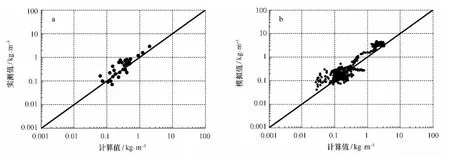
图2 挟沙力公式（28）采用全潮平均动力因子形式的验证

图3 挟沙力公式（28）采用半潮平均动力因子形式的验证

4 结论

论文根据近岸浪、潮、流等动力因子的特征，提出了海洋波动有效速度并明确了其表示方法及物理意义，其为表征近岸多动力条件作用下的水体平动动能的速度。在平衡时的水沙界面通量的条件下，结合海洋波动有效速度推导得到了一个新的适用于近岸海域的挟沙力公式。并得到了以下结论：

（1）在近岸海域的挟沙力计算中，采用海洋波动有效速度形式的动力因子与常用的半潮平均或全潮平均形式的动力因子相比计算结果更为准确。

（2）对于振荡流如潮流和波浪等引起的水体流动，海洋波动有效速度为最大水平速度的倍，对于河流和海流，有效速度即为其流速。

（3）水流挟沙力与临界速度有关，且该临界速度是水深和相对糙率的函数。水深越大临界速度越大；相对糙率越小，也即床面越光滑，临界速度越大。

［1］ 刘家驹.连云港外航道的回淤计算与预报［J］.水利水运科学研究，1980，4：31－41.

［2］ 刘家驹.海岸泥沙运动研究及应用［M］.北京：海洋出版社，2009.

［3］ Zhang Jinshan，Lu Peidong，Xu Ming.Numerical modeling on suspended sediment transportation in the Hangzhou Bay［J］.China Ocean Engineering，1998，12（1）：87－98.

［4］ 窦国仁，董凤舞.潮流和波浪的挟沙能力［J］.科学通报，1995，40（5）：443－446.

［5］ Guo Qingchao，Jin Yee－Chung.Modeling sediment transport using depth－averaged and moment equations［J］.Journal of Hydraulic Engineering，2000，125（12）：1262－1269.

［6］ Dou Xiping.Sedimentation problems related to regulation of deep channel in the Yangtze Estuay［C］//Proceedings of the International Conference on Estuaries and Coasts.Hangzhou：Zhejiang University Press，2003：36－45.

［7］ 张瑞瑾.河流泥沙动力学［M］.北京：水利电力出版社，1989.

［8］ Xie Jun，Yan Yijun.Promoting siltation effects and impacts of Hengsha east shoal on the Yangtze River estuary［J］.Journal of Hydrodynamics，2011，25（5）：649－659.

［9］ Mo Wenyuan，Wei Xing，Qiu Liguo.A long－term numerical model of morphodynamic evolution and its application to the Modaomen Estuary［J］.China Ocean Engineering，2011，26（1）：123－138.

［10］ 曹祖德，李蓓，孔令双.波、流共存时的水体挟沙力［J］.水道港口，2001，22（4）：151－155.

［11］ Zhang Qinghe，Yan Bing，Wai Onyx W H.Fine sediment carrying capacity of combined wave and current flows［J］.International Journal of Sediment Research，2009，24（4）：425－438.

［12］ 李瑞杰，罗锋，朱文谨.悬沙运动方程及其近底泥沙通量［J］.中国科学E辑：技术科学，2008，38（11）：1995－2000.

［13］ Lick Wilbert.Sediment and contaminant transport in surface waters［M］.New York：CRC Press，2009.

［14］ 郑俊.近岸水沙界面通量与挟沙力关系及其应用研究［D］.南京：河海大学，2012.

［15］ Soulsby，Richard.Dynamics of Marine Sands［M］.London：Thomas Telford Press，1997.