煤田声波测井曲线预测方法的对比研究

林庆西，彭苏萍，师素珍，李 娟，汤 尧，喻梓靓

(中国矿业大学 (北京)煤炭资源与安全开采国家重点实验室，北京100083)

在地震解释及反演中，声波测井资料是重要的基础资料之一［1－2］，其不仅是测井和地震相结合的桥梁，而且是获得高分辨率地层波阻抗资料的关键，并且其质量高低，直接影响到地震解释反演的最终结果。然而，由于测井技术水平落后以及资金等情况的制约，在一些煤田采区经常会有测井资料不完整甚至缺失的情况。因此，对声波测井资料进行针对性地预测是很有必要的。

声波测井曲线的预测就是利用周围某邻域范围内已钻探井的地质、测井资料以及地震数据等，预测目标井中速度曲线的变化［3］。目前，常用的声波测井曲线预测方法有3种:经验公式法、地震属性分析法和神经网络法。在早期煤田勘探中，经验公式法在预测声波测井曲线中得到较为广泛的应用［4］。然而随着勘探开发的深入，对地震反演精度的要求越来越高，对反演所用的声波测井资料的要求也不断提高。其中，地震属性和神经网络方法在声波曲线预测中也开始逐渐得到重视，并进行了广泛的研究［5－8］。本文以顾桥矿区作为实例，分别利用这3种方法对声波测井曲线进行了预测，并对其预测的效果进行了对比研究。结果表明，从经验公式预测到属性分析，再到神经网络预测过渡时，预测能力持续提高。

1 预测方法原理的分析

从地质上来看，对于同一地质目标，可以用不同的地球物理方法来探测，从而得到不同的物理响应，得到不同的物理参数。这些不同信息之间的差异，来自于同一地质体综合映像的反映，表现出的不同特征之间应具有某种相关性和互补性，这也意味着它们之间可以通过某种方法进行转换。这就为声波测井曲线预测的可行性提供了有利的岩石物理基础［9］。实际上，无论是测井参数或者是地震数据，都反映了一定的地质特征，即反映了某种地质参数及其变化的规律。这表明研究区域内目标测井值，能够从周围邻域内各点的区域化变量值中得到估计［10］。

1.1 经验公式法

经验公式法主要是指利用一些经验公式或统计关系式，针对井周围一条或多条特征曲线进行的曲线预测，是一种井之间的数据转换关系。这种方法多用于没有声波测井曲线的地区，它可以对曲线进行快速预测。最常用的经验公式是Gardner公式和Faust公式。

Gardner公式揭示了在许多沉积岩系中，其速度和密度之间的一种简单的关系。Faust公式是一种速度－电阻率转换公式，其主要利用电阻率和深度值预测速度曲线［11］。除了上述2种经验公式法，在实际预测中，还有诸如统计拟合法、信息加权等方法［12］。这些方法都可以快速方便地获得声波曲线，在沉积岩层中应用取得了很好的效果。但是，其在煤层中的应用还有很多限制，比如用Gardner公式转换的速度大大低于煤层速度，而用Faust公式转换的速度又大大高于煤层速度。同时，无论采用什么公式，进行何种线性变换，都只是采用了一条或几条测井曲线进行声波曲线的预测。

1.2 地震属性分析法

地震属性通常被认为是一种地震道数据的任意数学变换结果，其在预测测井曲线中得到了广泛的应用［13］。Schultz等人首先提出利用多元地震属性预测测井的特征，认为预测的关键是找出物理参数和地震属性之间的关系，并通过分析井周围的一组训练数据来获得测井与地震数据的统计关系［14－15］。此方法主要有2种:单属性分析和多属性分析。

单属性预测是指只应用一种地震属性与已知声波测井曲线建立关系，再将这一关系应用到目标区域来预测声波测井曲线特性。在做声波预测时，对给定的各种地震属性，分别将其与目标测井数据做交会，获得目标数据与地震属性间最佳统计关系。

多属性分析是常规线性分析的一个推广，其主要通过多个最优属性来预测声波测井曲线，并结合地震属性中获得互补的特征来分辨目标测井数据的细微特征。由于目标测井曲线的频率成分比地震属性高得多，一般采用褶积算子对地震属性与目标测井曲线进行相关，即认为测井曲线每个样点与一段连续的地震样点相关联。在选取最佳地震属性时，一般是采用次最优方法，即逐步回归法。相对于穷举搜索法，此方法尽管不一定是最优解，但计算时间远远小于上述的方法［16］。

类似于经验公式法，地震属性分析法也是利用统计关系来预测声波曲线，只不过它不是利用某一条或某几条测井曲线，而是对整个地震数据属性进行线性运算。此方法可预测性更强，预测精度更高些。另外，这种方法不仅局限于声波曲线的预测，还可以预测其他类型的测井曲线，如孔隙度、密度等，因此在实际生产中获得了广泛地应用。然而，地震属性分析法也有局限性，那就是必须使用训练数据来获得统计关系。对于完全缺失声波曲线的地区，是无法进行预测的，必须先利用经验公式法做已知测井曲线的转换，经验证后的速度值满足一定的条件，再利用地震属性分析法进行合理地预测。

1.3 神经网络法

从本质上来讲，神经网络法也是借助地震属性进行目标井特征的预测。但是，地震属性分析法中所涉及的曲线与属性关系为线性关系，而实际上，一些非线性关系也能用来预测测井特征，神经网络法就可以帮助确定这种最佳的非线性关系［17］。神经网络有很多种类型，主要介绍多层前馈神经网络(MLFN)和概率神经网络(PNN)2种类型。

前馈神经网络(MLFN)是一种最简单的神经网络设计。“多层”的意思是指这一类型网络具有多个计算单元层，这些计算单元通常以前馈的方式进行连接。MLFN是用以预测测井曲线的最常用的神经网络。作为一种传统的神经网络，MLFN由一个输入层、一个或多个隐含层和一个输出层组成［18］。如图1(a)所示。与线性多属性分析相比，MLFN的优点是在属性值域的多数区域，模拟的数据都比用线性回归法好。缺点是在属性值小的情况下，要使神经网络对数据拟合得很好的话，会造成明显的不稳定性。

概率神经网络 (PNN)实际上是一种采用神经网络结构实现的数学内插法，类似于井的克里金插值法。与MLFN一样，PNN也是一种前馈神经网络。但是PNN有4层结构:输入层、模式层、累加层和输出层，如图1(b)所示。相对于MLFN，PNN方法的优势为:不依赖于一组初始权重，权重值完全由数据来确定，并且最终集中于一个解决方案;PNN网络具有一定的抗噪性能，即可以包容一定的错误样本。PNN的缺点为，其要存储和转换所有训练数据，并将每个输出样本与每个训练样本进行比较，因此神经网络的计算需要电脑高速的运算能力，且通常运算速度会很慢。

同地震属性分析法一样，神经网络法也是建立地震属性与目标测井数据的关系。但由于神经网络模型可以成功地确定地震数据和测井数据间复杂的非线性关系，神经网络法预测的测井值可能会更为精确，但也有其自身的限制条件。首先，神经网络法需要利用训练数据进行训练，得到所需的非线性关系。神经网络如果没有经过训练，它是不能推导或预测数据的。其次，神经网络只能应用于训练窗口的范围内，这是因为如果应用到整个数据窗口，神经网络的运行时间会变得非常长。另外，神经网络也不适合推断训练数据边界之外的区域。

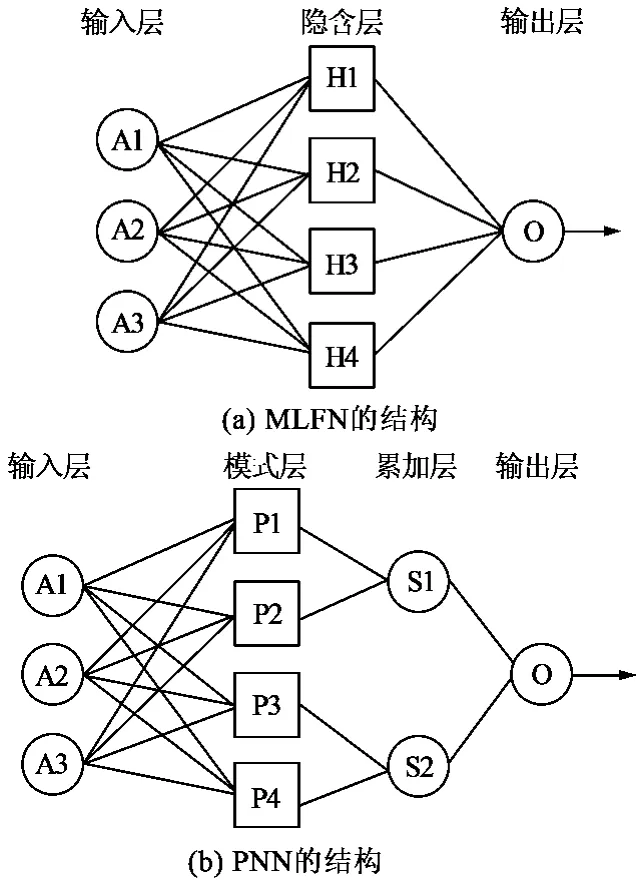
图1 神经网络的结构

2 实例应用

以顾桥煤田某研究区为例，对比研究上述3种预测方法。顾桥煤田采区位于安徽省的西部，勘探面积为23.325km2。主要研究煤层为13－1，11－2，8，6－2，1煤，其埋藏深度大致分布于500～900m之间，并作为此次研究的分析窗口。研究区内共有64口测井，且均匀分布于研究区的各个位置。经统计，每口井都有密度曲线，但只有29口井包含速度曲线，可以作为此次研究的训练样本和目标。

2.1 预测方法的应用

为了能够可靠地利用这些方法进行预测，首先需要对已有的曲线进行预处理工作。预处理包括环境校正、测井曲线标准化与校正等，以确保测井曲线能真实反映地层情况［19－20］。之后再分别利用3种方法进行实际预测。

2.1.1 经验公式法的应用

本例中由于所有井都有密度曲线，而且曲线形态与地层反映良好，所以采用Gardner公式法。对区内兼有速度和密度曲线的29口井做代入运算，得到适合该地区的Gardner公式。再将剩余井代入此式中，得到目标预测值。选取其中一口预测井如图2所示。

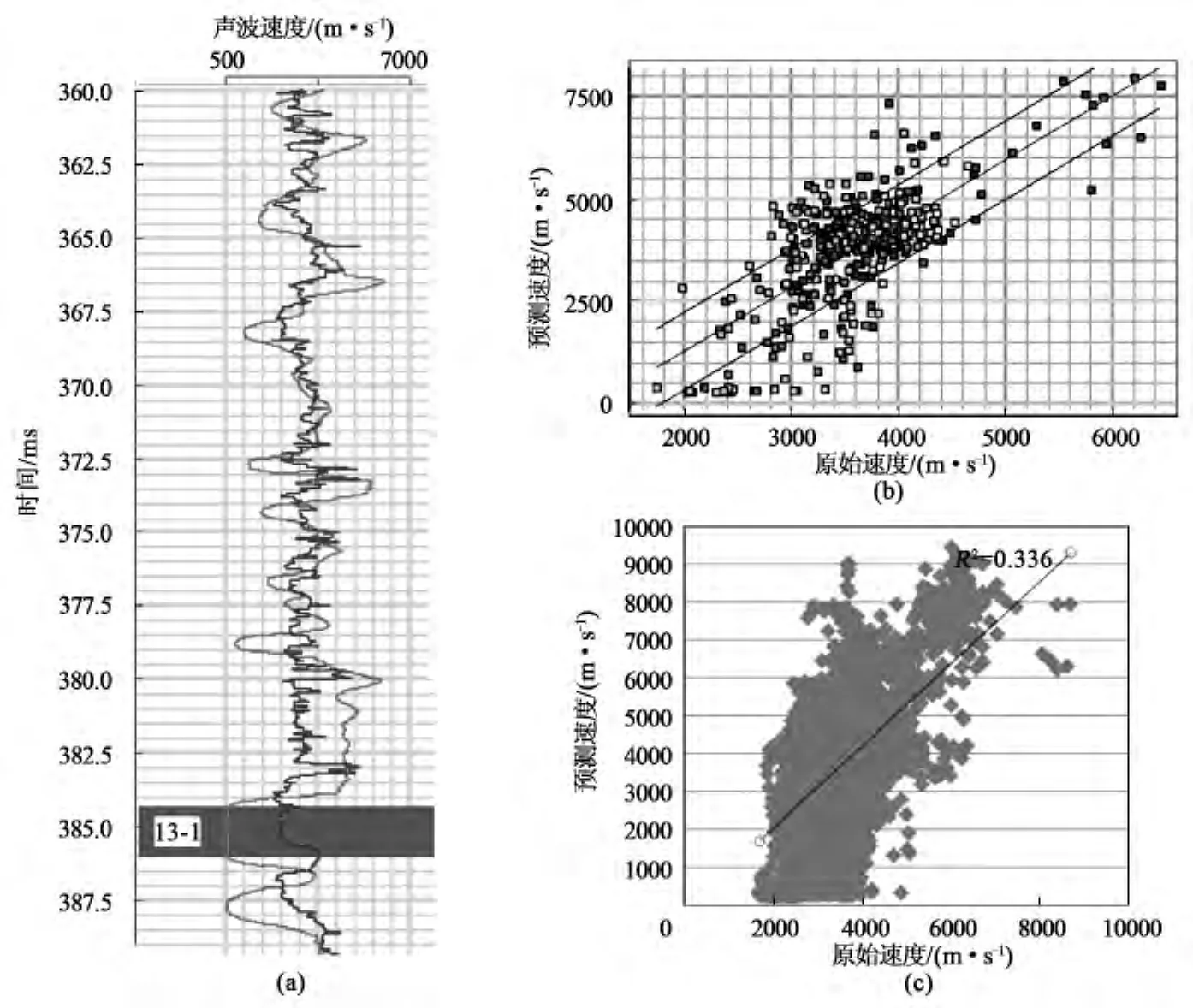
图2 利用经验公式法预测目标井的声波速度曲线

图2(a)显示的是预测速度曲线(浅色)与 原始速度曲线 (深色)。图2(b)显示的是在一个恒定采样间隔的分析窗口内，预测速度与原始速度曲线的一个交会。通过计算预测曲线和原始曲线的相关性，其相关系数大概为0.336，如图2(c)所示。可以看到，相关性较小，利用公式法求取的预测曲线精度不高。但是由于其简洁的方法和步骤，在完全缺失声波资料的矿井研究区，可以在一定的误差范围内，用来预测声波曲线。

2.1.2 地震属性分析法的应用

利用地震属性预测声波曲线，首先需要导入三维地震数据体。在本例中，地震数据体共包含1109条 inline线和1819条 crossline线，间隔为5m。然后，建立好几何网格，使得地震数据和测井曲线能位置统一。以上文已知的29口井作为训练样本，抽取复合地震道，并对其进行转换运算，得到多种体属性值。同时利用基于模型反演获得的波阻抗体，提取出外部属性值 (外部属性用ex_ attr来表示)。最后建立地震属性与井数据的线形关系，其中部分关系如表1所示。分析窗口为13煤和1煤之间的区域。

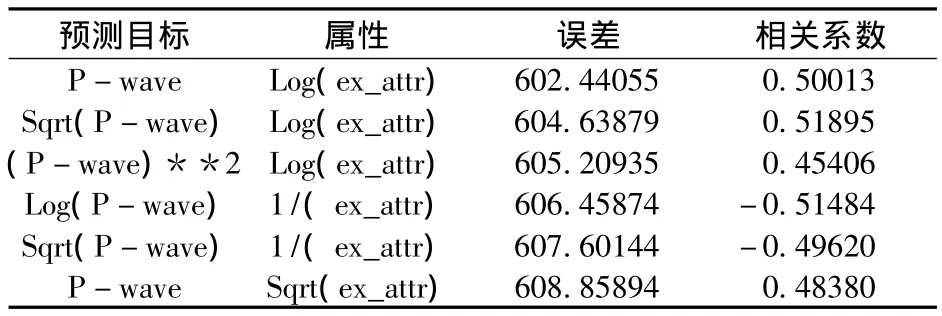
表1 单属性分析

从表1中可以看出，最佳的属性表达式为Log (ex_attr)，属性运算的误差率最低，且相关系数大约为0.50，相对比较高。因此选取其作为单属性分析的结果。图3(a)显示了其中三口井利用单属性分析所获得的预测结果。

图3 利用地震属性分析法预测声波曲线

多属性分析是在单属性分析的基础上，利用逐步回归法进行分析与计算。在本例中，使用的最优褶积算子长度为10，获得的分析结果如表2所示。

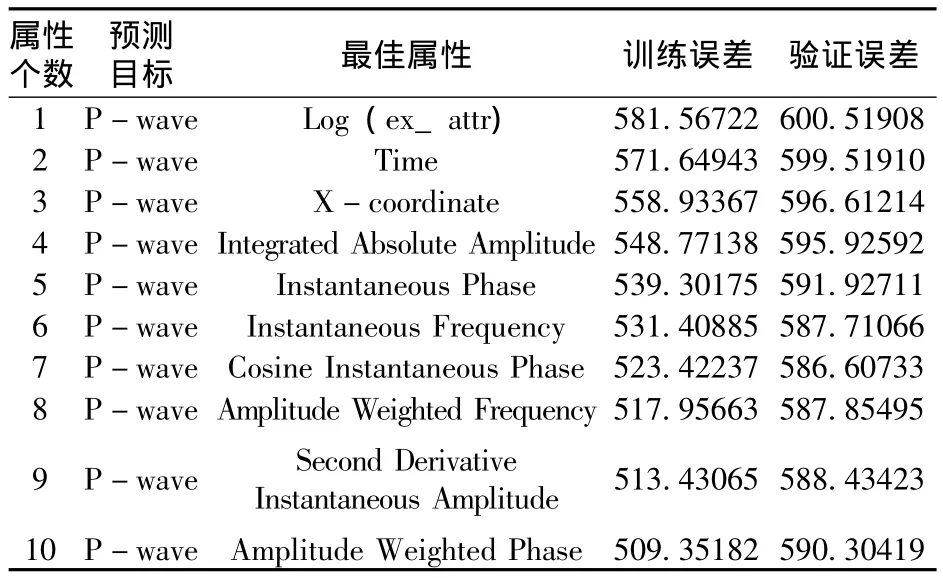
表2 多属性分析

在表2中，每一行代表一个多属性变换，且此变换包含了上面所有行的属性变换。多属性分析预测结果见图3(b)。当应用多属性分析时，会出现过度训练的情况，需要对训练误差和验证误差分别进行计算。结果如表2中后两列所示。过度训练是多属性分析中的一种特殊情况，即增加属性只是简单地预测了测井数据或属性本身的细节或者噪声，甚至可能会使结果变得更糟。解决这一情况需要使用交叉验证的方法。本例中的验证结果如图4所示。

在图4中，下方斜线表示所有井的预测误差，随着新属性的加入，曲线逐渐下降。上方较平缓线表示平均验证误差。它是通过“隐藏”某一口井并利用算子计算其他井来预测此口井的预测值，从而获得验证误差值。从图4可以看出，验证误差在第7个属性时为最小，然后逐渐增加。因此本例中应选取表2中的前7个属性来做多属性分析。

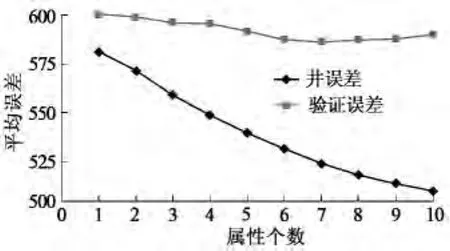
图4 交叉验证法的预测结果

对比单属性分析的归一化相关系数0.50，利用多属性分析获得的归一化相关系数为0.66，多属性分析的预测精度要略高于单属性分析。

2.1.3 神经网络法的应用

通神经网络算法主要是利用多属性变换得到的属性作进一步的训练与分析。在本例中，将表2中的前7种属性作为网络输入，并以井孔目标声波曲线作为期望输出，建立神经网络结构。根据期望输出和实际输出之误差，调整输入层和输出层之间的各个连接权，使期望输出和实际输出之间的差异达到最小。当网络收敛且网络整体方差达到要求的精度时，便完成网络训练。本例中对于MLFN，根据误差最小原则，确定出隐含层节点数为46，共轭梯度迭代次数为100，总的迭代次数为10。对于PNN，确定出σ因子数量为25，σ因子取值范围为0.1～3.0，共轭梯度迭代次数为20。

最后利用训练好的2种网络，对非目标声波曲线分别进行预测，得到的预测结果如图5(a)和图5(b)所示。

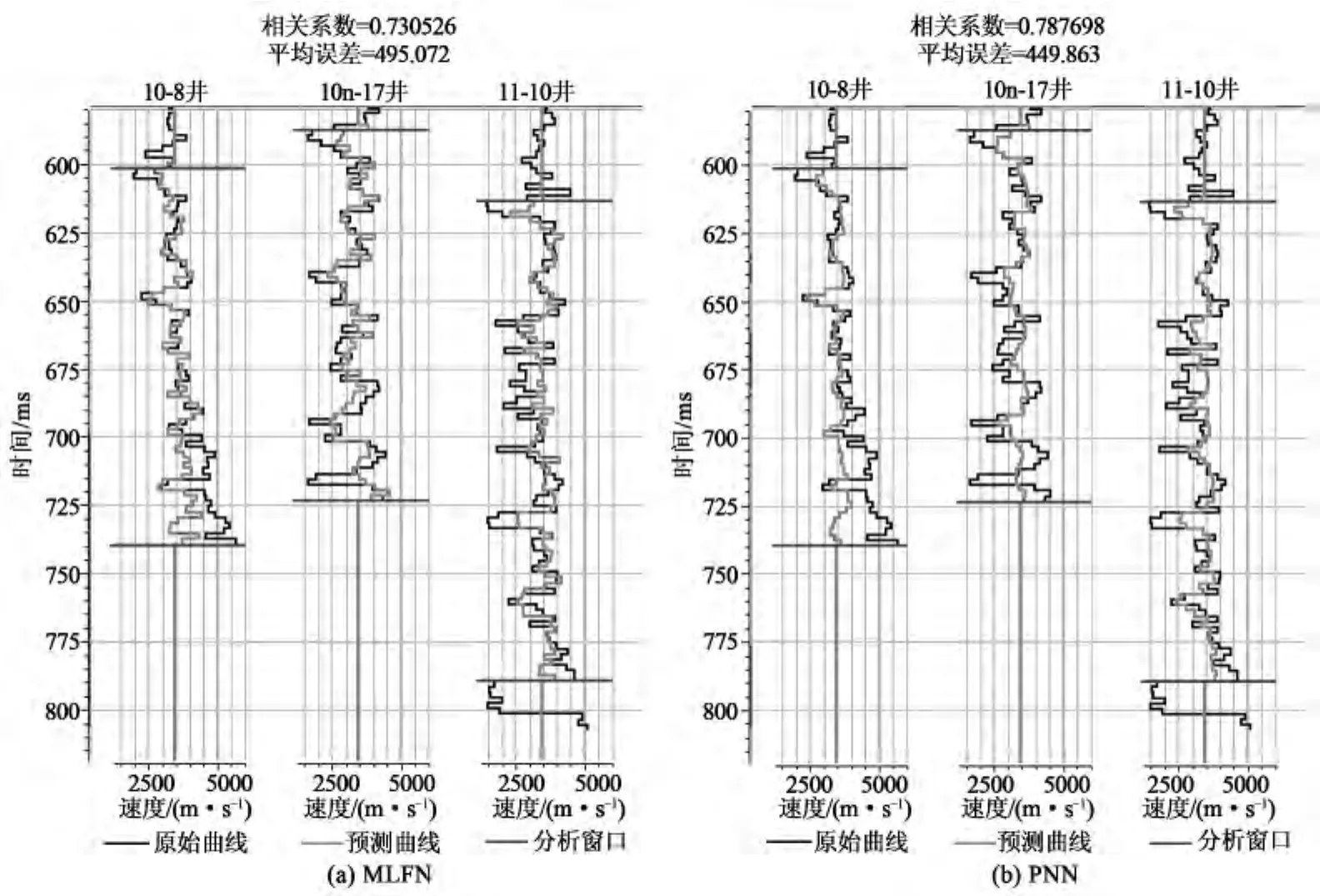
图5 利用神经网络法预测声波曲线

图5中，利用MLFN得到的归一化相关系数约为0.73，利用PNN得到的归一化相关系数约为0.79。PNN的预测精度要高于MLFN，这是因为PNN利用其算子包含了所有的训练数据信息，并且比较了每个输出样本和训练样本。同时，与MLFN相比，PNN的独立权重完全取决于整个数据体。

2.2 结果对比分析

利用3种预测方法对整个研究区内的声波速度曲线进行了预测，并得到了不同精度的预测结果，随机挑选其中一口井作对比，采样率选为2ms，其预测结果如图6所示。

根据图6中原始曲线与预测曲线的匹配情况，可以明显看到其预测精度从左往右是逐步升高的，归一化相关系数从0.355提高到0.912。利用PNN预测的声波曲线与原始曲线基本保持一致。因此对比其他的方法，利用PNN方法预测速度曲线其精度更高，获得的预测结果最佳。

另一种测试PNN方法准确性的方式是比较三维速度体，它是通过将预测结果应用到整个三维地震数据体中获得的。利用不同方法获得的速度体如图7所示。由于利用经验公式法得到的预测精度较低，且只能对单一测井数据进行运算。在使用经验公式法预测声波速度体时，只能使用插值法，且获得的速度体十分粗糙。因此，在图7中忽略了利用经验公式法预测得到的声波速度体。

图6 应用不同的方法预测井11_8的声波速度曲线

图7 应用不同的方法预测得到的声波速度体

从图7(a)可以看到，由于煤层速度要低于围岩速度，单属性分析获得的声波数据体中煤层的颜色显示明显。分析区间其他速度层位也十分明显。图7(b)中，多属性分析获得的速度值变化较多，特别对于煤层处，有速度值明显的变化，其结果比单属性分析要略好一些。图7(c)中的MLFN预测速度层位不连续，不是很好。但对于煤层处，其速度值变化要更为明显。对于图7(d)中的PNN预测速度体要明显好于上面3种方法。不仅煤层的速度层位清晰，而且可以看到不同层位处的速度值变化比较平均。分辨率提高了很多，适于做速度体的分析以及速度值的提取。对构造煤有很好的预测作用。

通过对不同方法获得的预测结果进行比较，可以看到，PNN给出了更好的声波速度分布图像。这是因为其能获得地震属性与速度曲线间更好的非 线性关系。

3 结论

(1)利用经验公式法预测声波测井曲线，只是对一种或几种测井曲线进行数学转换，因此预测结果较快且容易掌握，但得到的预测结果精度不高。其主要适用于缺失测井曲线或地震数据极差的地区。

(2)地震属性分析法是利用整个地震数据体进行预测，利用横向和纵向的线性拟合来建立地震属性与目标测井曲线的线形关系，其预测精度要高于经验公式法。

(3)神经网络法可以建立地震数据和测井数据间的非线性关系，训练时间较长，但在煤田中，其预测声波测井曲线的精度要高于上述2种方法。神经网络法是预测声波测井曲线的最佳方法。

(4)利用神经网络预测声波曲线之前，需要做属性分析，在计算上两者有一定的继承性。进一步改善多属性拟合的预测精度，可以得到更高的神经网络预测精度，能够为后续的地震反演提供可靠的声波速度曲线。

［1］杨志力，周 路，彭文利，等.BP神经网络技术在声波测井曲线重构中的运用［J］.西南石油大学学报 (自然科学版)，2008，30(1):63－66.

［2］张兴岩，潘冬明，张 华，等.波阻抗反演在提高煤层分辨率上的应用［J］.煤炭科学技术，2009，37(1):96－98.

［3］陈 亮，熊琦华，王才经.虚拟井预测法及其应用［J］.石油大学学报(自然科学版)，1997，21(5):16－20.

［4］彭苏萍，孔 炜，杨瑞召，等.煤田反演的声波测井曲线重构［J］.北京工业职业技术学院院报，2003，2(4):11－16.

［5］孔 炜，杨瑞召，彭苏萍.地震多属性分析在煤田拟声波三维数据体预测中的应用［J］.中国矿业大学学报，2003，32 (4):443－446.

［6］张永军，程 超，梁 涛，等.基于BP神经网络的测井曲线构建［J］.西部探矿工程，2006，18(2):82－85.

［7］张丽红，师素珍，袁 莉，等.多属性技术在底板砂岩富水性预测中的应用［J］.北京工业职业技术学院学报，2011，10(3):1－3.

［8］张亚斌，瞿亦斌，陈忠云.神经网络技术在测井曲线重构中的应用［J］.石油天然气学报，2011，33(3):89－94.

［9］沈向存，杨江峰.声波曲线重构技术在地震反演中的应用［J］.中国西部油气地质，2006，2(4):436－439.

［10］李忠荣，马先林，周坤瑞，等.虚拟井测井曲线的预测技术［J］.石油大学学报 (自然科学版)，1994，18(4):20－25.

［11］Faust L Y.A Velocity Function Including Lithology Variation［J］.Geophysics，1953，18(2):271－288.

［12］贺 懿，刘怀山，毛传龙，等.多曲线声波重构技术在储层预测中的应用研究［J］.石油地球物理勘探，2008，43(5).

［13］石双虎，何樵登，滕吉文，等.利用多元地震属性预测测井特性［J］.西北地震学报，2006，28(4):309－313.［14］Schultz P S，Ronen S，Hattori M，et al.Seismic－guided Estimation of Log Properties，Parts 1［J］.The Leading Edge，1994，13(5):305－310.

［15］Hampson D P，Schuelke J S，Quirein J A.Use of Multiattribute Transforms to Predict Log Properties from Seismic Data［J］.Geophysics，2001，66(1):220－236.

［16］Draper N R，Smith H.Applied Regression Analysis［M］.Michigan:John，Wiley＆Sons，Inc.，1966.

［17］Ronen S，Schultz P S，Hattori M，et al.Seismic－guided Estimation of Log Properties，Parts 2［J］.The Leading Edge，1994，13 (6):674－678.

［18］LIU Zheng－ping，LIU Jia－qi.Seismic－controlled Nonlinear Extrapolation of Well Parameters Using Neural Networks［J］.Geophysics，1998，63(6):2035－2041.

［19］彭苏萍，邹冠贵，李巧灵.测井约束地震反演在煤厚预测中的应用研究［J］.中国矿业大学学报，2008，37(6).

［20］LIN Qing－xi，SHI Su－zhen，LI Shan－shan，et al.Application of Well Log Normalization in Coalfield Seismic Inversion［J］. Journal of Coal Science＆Engineering，2013，19(2).