基于小波预处理的基坑变形监测数据的最小二乘估计
邱建昌,袁昌茂
(1.惠州建昌测绘有限公司,广东 惠州 516100; 2. 广西地理信息测绘院,广西 柳州 545000)
基于小波预处理的基坑变形监测数据的最小二乘估计
邱建昌1,袁昌茂2
(1.惠州建昌测绘有限公司,广东 惠州 516100; 2. 广西地理信息测绘院,广西 柳州 545000)

利用小波变换特有的低通滤波属性和有效抑制测量噪声的能力,将传统的最小二乘估计与之相结合,提出了一种基于小波预处理的最小二乘估计新方法,并针对具体基坑变形监测数据,验证了该方法的有效性。
小波变换; 最小二乘估计; 噪声; 拟合
研究基坑变形监测数据的估计理论中,常采用最小二乘法。传统的最小二乘法在估计精度要求比较高的情况往往不能满足要求。 由于监测数据不可避免地存在噪声,严重影响变形监测数据模型的质量。近几年出现的小波分析是一种相当好的数据预处理方法,它通过对采集数据的多尺度分解,最大限度地提取信号中各种有用信息,在预处理的过程中通过小波变换的低通滤波效应分析并找出各部分中的“异常”部位并去除可能的噪声部分,实现监测数据发展规律的本质还原。
1 小波分析基本理论[1,2]
小波变换就是在平方可积空间(f(t)∈L2(R))中,有Ψ(t),当其Fourier变换Ψ^(ω)满足允许条件:
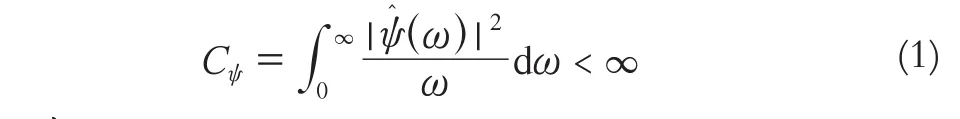
有小波函数为:
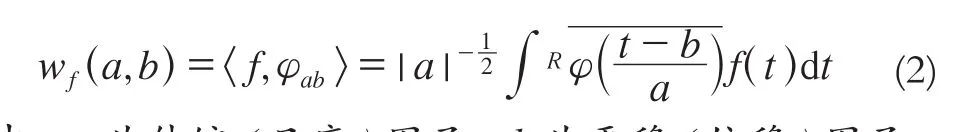
式中,a为伸缩(尺度)因子;b为平移(位移)因子;a,b⊂R。显然,当a>0时,伸缩因子才有直观的物理意义。
函数簇是基本小波函数通过伸缩和平移得到的。小波变换的基底为:

由于选择不同的参数a、b,就能构造不同尺度的小波基,在实际应用中,灵活选择函数因子,就能对真实信号形成良好的逼近,这不仅能对信号进行有效分解和提取,还能进行信号的分离和消噪。
多分辨率分析[3]:多分辨分析在函数空间L2(R)(一维平面平方可积)内,将函数描述为一系列近似函数,每个近似函数的极限都能恒等于该分量。多分辨分析实际上就是多尺度函数逼近,从某个子空间L2(R)出发,建立起可变化的基底,通过变换,再把基底扩充到能够覆盖整个L2(R),通过这样实现有效地逼近函数,实质上就是把整个平方可积的实变函数空间通过剖分转化成一系列的函数子空间。即是把L2(R)按一定的分辨率先分解成一串嵌套的闭子空间序列{Vj}j∈Z,然后通过正交补的塔式分解再将L2(R)分解为一串正交小波子空间序列{Wj}j∈Z,各函数空间关系如下:
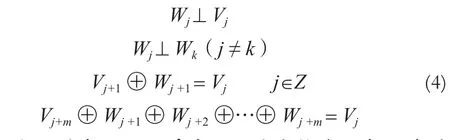
从上面的式子可以看出,小波变换能形成一系列不同尺度的序列,它的灵活变化可以提取包括从低频到高频信号的所有频谱数据,并且不重叠,所以有相当好的连通适应性。
2 最小二乘估计的原理
估计从数据和函数的整体考虑。估计函数p(x)同监测数据点(xi,yi)(i=0,1,…,m)误差ri=p(xi)-yi(i=0,1,…,m)的大小,通常有以下3种方法[4]:第1种是取误差绝对值的最大值为估计准则,即误差向量r=(r0,r1,…,rm)T的∞-范数;第2种是取误差绝对值的和为估计准则,即误差向量r的1-范数;第3种是取误差平方和的算术平方根为估计准则,即误差向量r的2-范数。前面2种方法虽然简单、容易构造,但不便于微分运算 ,第3种方法相当于考虑 2-范数的平方,因此在最小二乘估计中常用来度量误差估计模型ri(i=0,
1,…,m)的整体大小。
3 小波分析结合最小二乘估计的变形监测数据分析模型
变形监测最常用的数据分析模型[5]为:
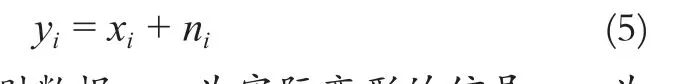
式中,yi为实际观测数据;xi为实际变形的信号;ni为噪声信号。实际上,观测数据的小波分析主用是利用小波分解的良好的逼近特性实现对观测数据的噪声消除,找出实际观测值y(i)中的实际变形信号xi。然后再利用最小二乘估计求出xi最佳逼近模型。具体做法是:对观测数据(xi',yi')(i=0,1,…,m),通过采用小波基底函数伸缩成不同的小波基对观测数据的逼近,然后形成{Vj}j∈Z和{Wj}j∈Z两串嵌套小波子空间序列,对蕴藏噪声的高频序列{Wj}j∈Z采用灵活的方法实现对噪声的消除,把低频部分{Vj}j∈Z和已经阈值处理过后的高频部分进行小波重构,得到去噪后的变形信号xi',最小二乘估计就是对xi'的估计。在取定的函数空间Φ中,求p(x)∈Φ,使误差ri=p(xi)-xi'(i=0,1,…,m)的平方和最小,即

从几何意义上讲,就是寻求与去噪后的数据点(xi',yi') (i=0,1,…,m)的距离平方和为最小的曲线y=p(x)(如图1)。函数p(x)称为拟合函数或最小二乘解,求拟合函数p(x)的方法称为观测数据拟合的最小二乘估计。
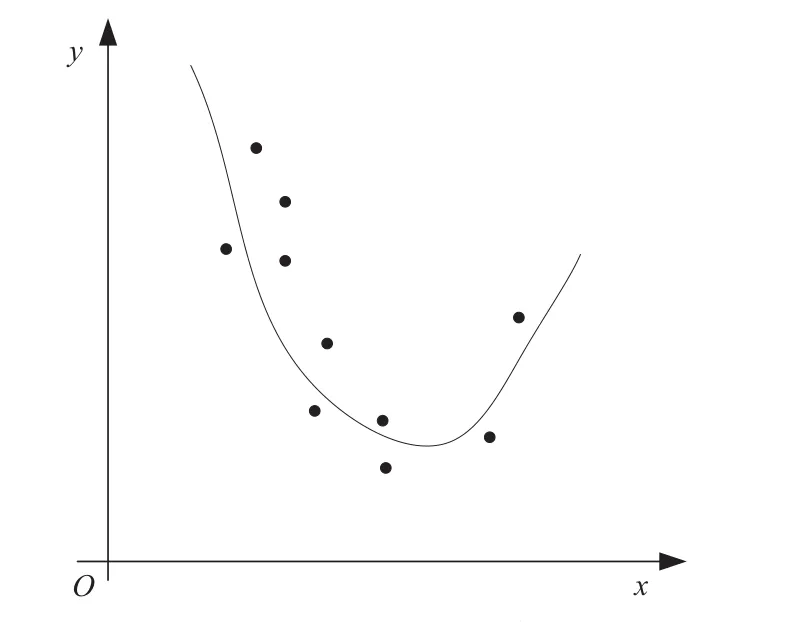
图1 最小二乘拟合
曲线拟合函数的构造。设M=span{x1,x2,…,xn}为内积空间U的n维线性子空间,x∈U。又设为x在M中的最佳逼近,则根据投影性质,应有:
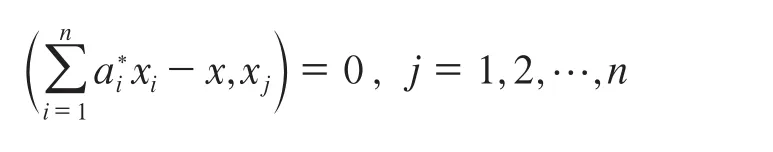
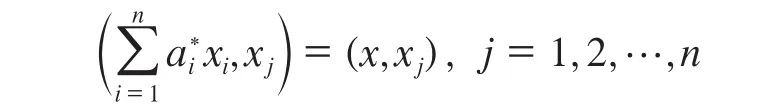
可由下面方程式求出:
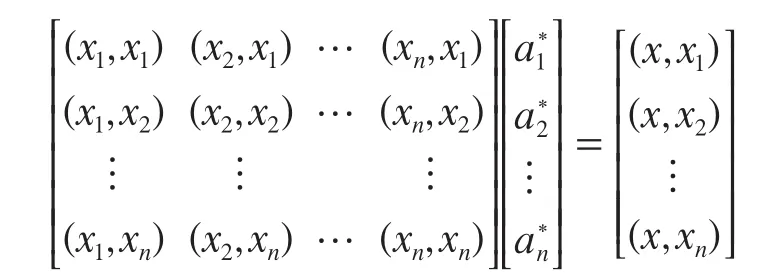
由于x1, x2,…, xn线性无关,所以,
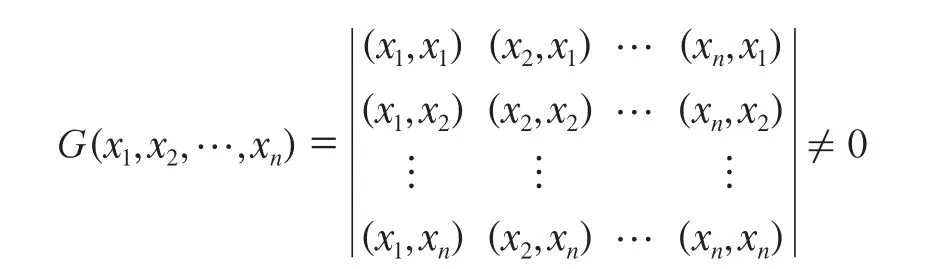
故方程组有唯一解,
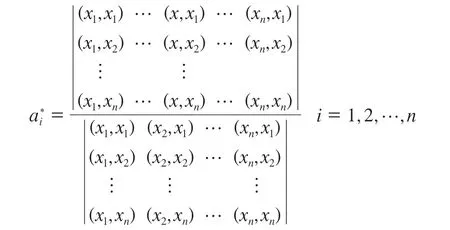
从而可求出x在M中的最佳逼近元,即
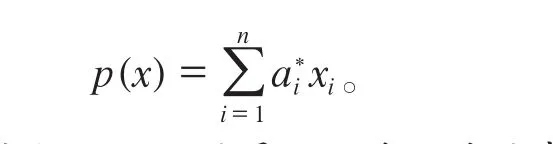
基于小波变换预处理的最小二乘估计的步骤:
1)变形观测数据的小波分解。信号的小波分解,先确定分解所用的小波函数(根据数据的平滑需要和噪声模型的适应性),确定分解的层数,然后按要求对变形观测数据进行分解。
2)阈值处理。选择合适的阈值,对第一层到第m层的细节信号进行阈值处理以去噪。在阈值处理中,最主要的是阈值的选取,它直接关系到信号和噪声的降噪质量,阈值选取不恰当会把有用的信号消除或者达不到去噪的目的。因此,要根据观测数据的噪声类型选择阈值范围。同时,选择理想的小波函数,以达到去噪的最优效果[6]。
3)小波重构。把低频部分和已经阈值处理过的高频部分进行重构,就得到去噪后的真正变形信号。
4)利用去噪后的变形观测数据进行最小二乘估计的模型构造。
4 实例分析
某地铁工程中的一个基坑,共观测了19期数据,数据精度足够,各基坑点布设如图2。本文小波预处理采用具有紧支集正交小波基的Daubechies小波,2层分解与重构,采用最大最小阈值去噪模式。
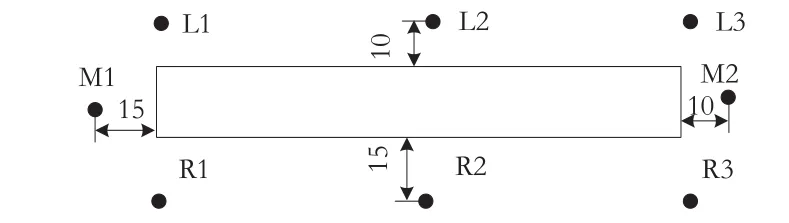
图 2 基坑点布设图
其原始观测的累计变形如图3。

图 3 累计变形图
经过小波去噪后,各基坑变形点累积变形图如图4。

图4 小波去噪后累积变形图
不同的变形点,其变形阶段不同,发展趋势线也不同,在最小二乘估计时也应采取不同的函数进行逼近拟合[7]。下面以L(3)点、M(2)点作为典型进行分析。
L(3)点的变形曲线和拟合曲线见图5。最后求得最小二乘拟合函数为:

为判断拟合的准确度,我们采取比较通用的数据估计均方差的评判标准:去噪后数据与最小二乘拟合数据的均方差为0.350 195,原始数据与最小二乘拟合数据的均方差为1.053 584,各点拟合均方差平方见图6。从数据标准差的角度看,去噪后最小二乘估计不仅提高了估计的精度,还取得比采用原始观测数据拟合高很多的数据均方差。

图5 变形曲线和拟合曲线图
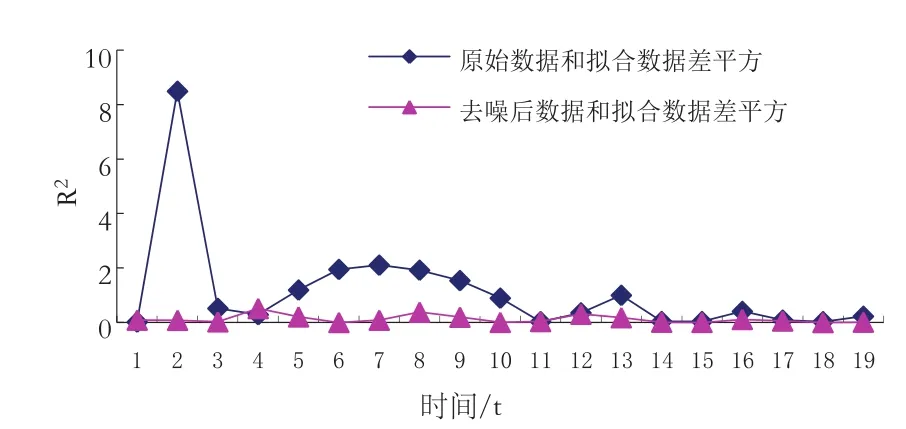
图6 拟合均方差图
M(2)点的变形曲线和拟合曲线如图7。
最后拟合函数为:
y=-0.003 8x3+0.210 2x2-3.657 8x+2.923 4
小波去噪后数据与最小二乘拟合数据的均方差为0.449 202,原始数据与最小二乘拟合数据的均方差为0.916 409,各点拟合均方差平方如图8。
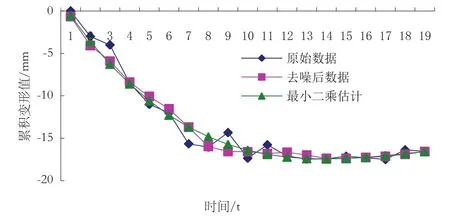
图7 变形曲线和拟合曲线图

图8 拟合均方差图
[1] 文鸿雁.基于小波理论的变形分析模型研究[D].武汉:武汉大学,2004
[2] 张正禄,黄全义,文鸿雁,等.工程的变形监测分析与预报[M].北京:测绘出版社,2007
[3] 林东,袁昌茂,文鸿雁. 小波多时间尺度分析在变形分析中的应用[J]. 地理空间信息,2010,8(2):143-147
[4] 鲁铁定.总体最小二乘平差理论及其在测绘数据处理中的应用[D].武汉:武汉大学,2010
[5] 莫颖军,袁昌茂,文鸿雁. 形变监测数据的多尺度滤波[J].城市勘测,2010(4):154-156
[6] 袁昌茂,文鸿雁. 变形监测数据处理的小波去噪方法[J]. 地理空间信息,2009,7(4):136-138
[7] 邹积亭,江恒彪,赵西安.基于小波去噪的地铁沉降监测分析[J].测绘科学,2007 (3):102-103
P207
B
1672-4623(2014)06-0135-03
10.3969/j.issn.1672-4623.2014.06.047
邱建昌,工程师, 研究方向为工程测量。
2013-12-19。
项目来源:广西自然科学基金资助项目(0991023)。

