关于量子力学-经典力学-相对论力学的统一性理论可行性研究——兼谈对测不准原理的大胆突破

周万连

中国地震台网中心，北京 100000

0 引言

在微观领域，量子力学与经典力学的矛盾之处在于，经典力学只有波动性而无粒子性，而量子力学虽有波动性和粒子性，但其却又是不连续的，现在，有没有一种可能使二者联系起来，经笔者研究，认为存在着这种可能性。由于这种可能性，就又使量子力学-经典力学-相对论力学相统一起来。

1 普朗克黑体辐射实验中得出的量子化可以变为连续的

1）跷跷板效应及电子的波形，及对测不准原理的大胆突破

笔者在《续论与连带性能量保留即能量不守恒有关的几个问题》（科技传播 2014 第3期）中论述了电子受高频或低频辐射后会产生跷跷板效应。即，当电子受高频辐射时，光子被反射掉，电子被辐射位置振幅增大，频率升高，从而此处膨胀，这时电子质心必向此处偏移，而相反处频率则稍低，故电子轴心必向相反处偏移，质心与轴心背离，继而，，由于相反处相对于被辐射点处的半径相对短些，因而，根据角动量守恒，相反处的角速度必有加快的趋势，于是，质心与轴心又逐渐重合，在这一过程中，电子因轨道外侧频率高于内侧，因此，其必向轨道内侧进动，轨道变狭长，从而向高能级跃迁，这在电子轨道1/4周时即完成，在第2个1/4周时，电子由于质心轴心再度趋于重合所产生的涡旋力而发射光子，电子这时从远日点向近日点跃迁，这是高能级向低能级的转化，电子这时又向轨道外侧进动，轨道趋圆，因此，电子受高频辐射时，其波形，基本可看成是简谐波（但又与简谐波有所区别，我们称为闪波，似闪电波形），这是因为进动时，电子向远日点跃迁，轨道变狭长，我们知道，球体直径增大1倍，体积扩大8倍，因此，其振幅似为8/2π但因为8倍是3维的，而我们这里描述的是2维的，故8应改为h，，即普朗克常量，即跃迁时振幅有h/2π倍，再加上量子数n，nh/2π，此即为电子的动量矩。在此条件下形成的波的波形，相当于维恩公式所描绘的波形。

当电子受低频光子辐射时，被辐射位置频率降的很低，而相反处频率则相对较高，于是，轴心向被辐射位置偏移，而质心则向相反处偏移，由于相反处远离轴心，因而，角速度必同步稍有下降，但此时，被低频辐射位置频率更低，而且，半径更短，因而，角速度必加快，从而达到降频后的轴心与质心的重合，在此过程中，电子同样产生跃迁，只是方向相反，因为轴心靠向轨道外侧，故跃迁方向指向近日点，而后，电子在涡旋力的作用下，发射一颗光子，由于动能减少，电子只能仍维持原来的进动方向，即，进动方向也指向近日点，与受激跃迁时的方向一致，因此，电子受低频辐射时，其波形近乎于 左图，这相当于1/x的波形，这同瑞利-金斯公式描绘的图形近乎一致。

从上面分析来看，我们可得出以下几点结论：

（1）高频辐射和低频辐射的波形合起来，正好相当于普朗克黑体辐射公式，其波形近似于闪电，故曰，闪波，其实闪电本身，可能就是这种波形的放大；

（2）电子的轨道是可测的，这是对测不准关系的一个大胆突破。这是从跷跷板效应得来的；

（3）电子受激而产生的跷跷板效应，就是一个谐振子，因为电子受激时，外力被反射，但在这外力的作用下，电子内产生跷跷板效应，从而孕育一颗光子，并发射出去，发射出去后，电子的能量守恒（这里，先不论连带性能量保留，即能量不守恒），这就是回复力，当自发发射的光子再作用于其它电子上，就相当于再来一次，电子又振荡一次，因此，电子受激后产生的振动效应，就是一个谐振子；

（4）电子的波动，在计算时可用两种方法。高频辐射时用经典波动方程，加入量子化元素。低频辐射时，用欧拉-傅立叶级数中的2L为周期的公式加入含时项及量子元素等计算，f(x)取1/x，这两个计算方法，见后面2中之论述。

2）原子内电子的潮汐运动

第一，原子核内的质子与电子互射光子交换能量，它们的相互作用就使原子内始终如潮汐般的运动，即，某一质子、电子相互作用会引起其它电子质子的连锁反应，从而引起全部电子质子的移动，这种移动就像是多米诺骨牌，每时每刻都发生着变化，产生连续的潮汐运动。

第二，原子内的壳层结构与潮汐运动是统一的，即电子在原子内的排列并无内外层之分，而是随潮汐运动的起伏，每时每刻都发生着变化，具体到某一个电子，某一时刻处在p亚层，某一时刻其又处在s亚层等等，但对于原子本身来说，其p亚层或s亚层上始终布满着相对固定的电子数。

基于以上两点原因，可以认为原子内的潮汐波形就应该是电子的波形，但因为电子的波确实是量子化的，其本身不连续，然而潮汐运动中的所有电子在潮汐运动中却可以连成一个完整波形，即，每个电子都处在这统一波形的不同相位处，也就是说，当原子内某一电子受激后会引起整个原子内、以至于原子群中其所有电子的波动，而且，这些电子的相位都是可以衔接起来的，方向一致，这样，就有了统一的波，或者说，在微观领域同样存在着简谐振动和连续的简谐波，这正像上面所说的闪波，闪波，可能就是微观领域的连续波形。同样，普朗克黑体辐射中的谐振子，在特定的条件下也可以是连续的。否则，我们平常见到的日光就会是脉冲波了。

2 具体计算方法

升频用经典力学的波动方程，并加上量子化元素，以及连带性能量保留（即能量不守恒），即相对论力学元素。见，周万连《宇宙膨胀和能量守恒问题》科技传播2013，11（下）152。

Y＝nh/2πA COSωw+(t1－x/uw+)

这里w+＝万能比值，即 降温/升温，这是加入了相对论元素，即宇宙的膨胀系数。见，周万连《续论与连带性能量保留即能量不守恒有关的几个问题》科技传播 2014， 2（上）111，因为降温比升温用的时间稍长，它的比值就表示能量有所升值，即膨胀系数。下面的w-＝万能比值的倒数，表示下降趋势。

上式，即受高频作用时所用的公式

降频用欧拉-傅立叶级数公式，并加上量子化元素，以及万能比值，即，连带性能量保留（能量不守恒），即相对论力学元素，见下：

现取其和号后边部分，并加入含时项等，改为，

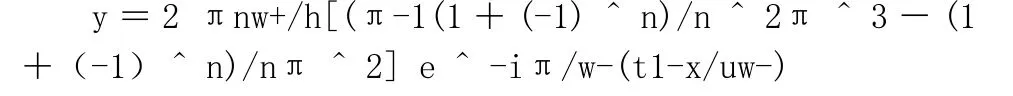
这里w-＝万能比值的倒数。表示趋于下降。而2πnw+/ h则表示在降频中，虽然用动量矩的倒数（表示下降），但仍有连带性能量保留发生，能量有微升，故加上一个w+，即膨胀系数。

实际上，以上两式都包含了相对论力学元素，因此相对论力学与其它两种力学的关系就不单独论述了。

但需要说明的是，在宏观领域，经典力学只要乘以万能比值（膨胀系数）w+，得出的就是相对论力学。

3 一点释疑

我在《续论与连带性能量保留即能量不守恒有关的几个问题》一文中，关于电子跃迁机理中认为，电子受高频光子辐射，进动方向趋于轨道内侧，跃迁方向指向远日点。但在实际中，电子有时有可能受外来光子辐射，有时也有可能受核内质子发射的光子的辐射，这两种辐射作用是不同的，前者肯定击中电子外侧，这同上文的解释是一致的。但核内质子发射的光子，必击中电子的内侧，按理说，此时电子进动方向应趋向轨道外侧，轨道应趋圆。如何解释此问题，我个人认为，第一种情况下，电子受激后，必向轨道外侧偏转一个角度，即远日点向外侧偏移一点，因为毕竟电子受力方向在外侧，但必须说明，电子轨道仍是狭长的，进动方向仍向轨道内侧；第二种情况下，电子的远日点必向内侧偏移一个角度，这是因为，原来电子就是外侧强于内侧，现在内侧转强，正好省略了跷跷板效应的一个过程，因为角动量守恒也正是要使电子内外侧平衡，由于这个原因，故电子的进动方向仍趋向轨道内侧，轨道仍狭长，只是两者向远日点跃迁的角度不同，二者呈90度角，左侧为核内质子的辐射跃迁方向，右边是受外来光子的辐射的跃迁方向，或者，反过来亦如此，这要看电子在核的哪一侧而定。

[1]周万连.宇宙膨胀和能量守恒问题[J].科技传播，2013，11（下）：152.

[2]周万连.续论与连带性能量保留即能量不守恒有关的几个问题[J].科技传播，2014，2(上):111.