A New Multi-objective Reliability-based Robust Design Optimization Method

Zichun Yang,Maolin Peng,Yueyun Caoand Lei Zhang

1 Introduction

For the past few years,the complication of multi-objective optimization,reliability based design,robust design and their combination of each other in real project had been paid more and more attention.The multi-objective reliability based robust design optimization(MORBRDO)takes into consideration the multi-objective.The designed product gets the expected reliability after MORBRDO and its multiobjective performances are the least sensitive to the design variables.There are several key problems must to be solved for MORBRDO:(1)calculation of structural reliability;(2)establishment of the robustness cost function;(3)the design of optimizing strategy;(4)implementation of multi-objective optimization.

When the ultimate limited state functions(ULSF)and the performance objective functions(POF)are given,the checking point method is often applied in reliability analysis,see Hasofor and Lind(1974);Rachwitz and Fiessler(1978);Santos et al(2012).The first order reliability index is numerically equal to the ratio of the mean value and standard deviation of the ULSF.However,for most of the structures in real projects,neither the ULSF nor the POF is known because of the complication of the shape,loads and boundary conditions.Theoretically,the mean value and standard deviation of the performance objectives and the structural reliability could be obtained by the Monte Carlo simulation method combined with the finite element analyses(FEA).But tremendous amount of computational work would make the Monte Carlo simulation method infeasible.Focusing on the listed problems,the researchers present a variety of methods.

When the ULSF and the POF are unknown,a dimension reduction method(DRM)is proposed to obtain the mean value and standard deviation,see Alois and Hans(2001);Rahman and Xu(2004);Lee et al(2008);Wang et al(2011)It converts the multi-dimensional integral to one dimensional integral.Similar to the Gaussian integral,it only calculates the values at some certain integral points and gets the mean value and standard deviation with the weighted sum method.The DRM provides an effective way to calculate the statistical moments,but the response surface method(RSM)is a more commonly used method.The essence of RSM is to simulate an approximate function to present the real relationship between the response and the random variables of the structure.And the approximate ULSF and POF can also be obtained by RSM,see Zhen et al.(2009);Shun et al.(2011);Adam and Tadeusz(2012).There are some commonly used forms for the response function,such as the quadratic polynomial function,see Cho JY,Oh MH.(2010);Kaminski and Szafran(2012),the Kriging model,see Andy(2009);Rajagopal and Ranjan G.(2011);Yang and Sun(2013)and the radial basis function model,see Zhou et al.(2013);Luo and Zhang(2012)Zhou(2013)compares the precision of several surrogate models and proposed a hybrid surrogate model.

The robustness cost function also often includes the mean value and standard deviation of the POF.The Taguchi quality loss function model is one of the most commonly used robustness cost functions,see Dubey and Yadava(2008).In other models,the six sigma robustness design idea is introduced,see Shimoyama(2008);Koch.et al(2004).Om et al(2010)proposes a hybrid quality loss function which included desirable as well as undesirable deviations;Lu and Zhang(2011)combines the reliability sensitivity with the performance objectives in robustness cost function.

The main challenge of MORBRDO is the low efficiency caused by large number of reliability analyses involved in the optimization procedure,especially when multifailure modes are within the structure.To improve efficiency,a sequential method is developed,see Yu.et al(2013)which decouples reliability analysis from the optimization to construct an equivalent deterministic constraint instead of the original probabilistic one by using the locally exponential approximation.Two singlelevel methods are proposed respectively,see Wang(2002);Du and Chen(2004),to instead the common two-level method.Li and Azarm(2006)presented a deterministic non-gradient based approach which applied a robustness index based on sensitivity regions.

The performance objectives will not always get the optimum simultaneously,sometimes even conflict with each other,see Besharati et al(2006);Li and Zhao(2013).A usual way is to turn the multi-objective optimization problem into a single objective optimization problem,such as the main objective method and the linear weighted sum method,see Om et al(2010);Lu and Zhang(2011).This way is easy to accomplish but can get only one or parts of the Pareto solutions.The aim of multi-objective design optimization is to obtain the Pareto solutions set with multi-objective design optimization algorithm,so that the decider could choose the corresponding one according to his preference to each objective.The way of changing the weight factors based on the linear weighted sum method is one of the most commonly used methods to get the Pareto solutions set,see Dubey and Yadava(2008).In recent years,the meta-metaheuristic method,see Darian and Alexander(2009),the Multi-Objective Tabu Search method(MOTS2),see Kipouros et al(2008);Trapani et al(2012);Razzaq et al(2013)the multi-objective particle swarm optimization algorithm(MOPSO),see Li and Zhao(2013),and the multi-objective evolutionary algorithm,see Rajagopal and Ranjan(2011),et al,are also applied to discover the full Pareto frontier for the multi-objective problems.These methods are being paid more and more attentions because they don’t need gradient of the objectives,so they are particularly suited for the structure with discontinuous POF.The main challenge of these modern ways is that they still need to decrease their iterations and improve their efficiency to reduce computational burden.

In this paper,a new MORBRDO model which takes advantages of the multi objective robustness,the reliability sensitivity robustness and the six sigma robustness design is proposed.And a new design optimization strategy is put forward to improve the optimization efficiency.The pure-quadratic polynomial functions are adopted to fit the POF and the ULSF of the structure.Then,the optimum design is obtained with the sequential quadratic programming method.Finally,three engineering projects are introduced to testify the feasibility,accuracy and efficiency of the new MORBRDO methodology.

2 Multi-objective reliability based robust design optimization(MORBRDO)model

2.1 traditional design optimization(TDO)model

Whereh(d)is the cost function of the structure with respect to d,gi(d)is theith constraint,d is thendv-dimention design variable vector,dLis the lower specification limit of d,and dUis the upper.The traditional(deterministic)design optimization model does not take the random character of the design variable and the non-design variable into consideration,and its optimal result locates on the constraint boundary,so the result is sensitive to the variables.And the structural reliability after design can not reach the requirement.

2.2A new MORBRDO model

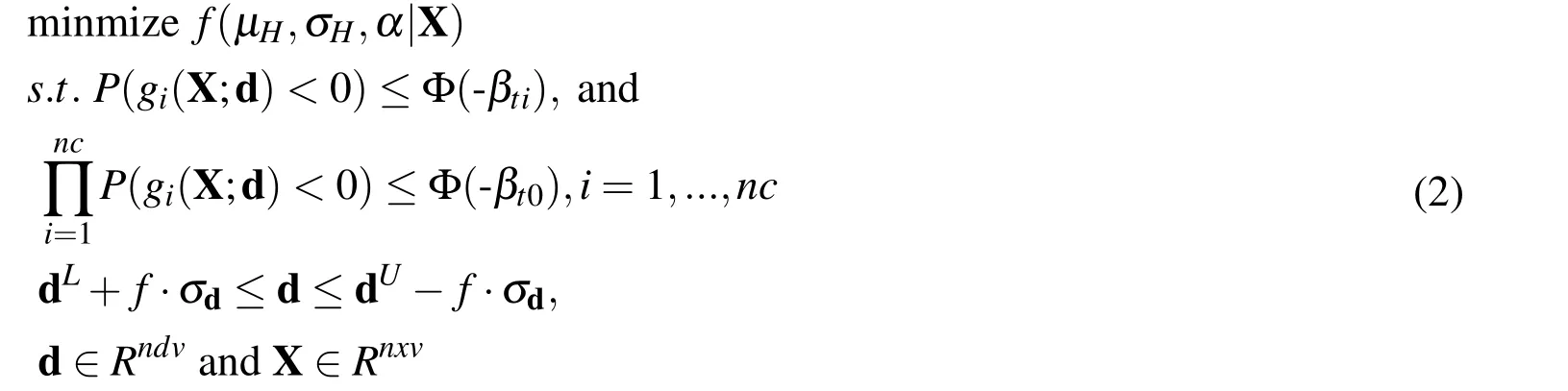
Wheref(µH, σH, α |X)is the new MORBRDO robust cost function with respect to α and X, α is the reliability sensitivity coefficient,X is thenxv-dimention variable vector(include design variable and non-design variable),µHand σHare the mean value vector and the standard deviation vector of the multi-objectives,respectively.σdis the standard deviation ofd.gi(X;d)is theith ultimate limit state function with respect to X,the design is assumed to be a “failure”ifgi(X;d)<0;βtiis theith target structural reliability index corresponding to thegi(X;d);P(gi(X;d)<0)is the probability ofgi(X;d)<0.Φ(·)is the standard normal cumulative distribution func-0);βt0is the target reliability index of the structure system under multi-failure modes.fis the robustness level of design variables,it guarantees the probability that the design point goes beyond the specification limits equal to or less than Φ(-f);Usually,3≤f≤6.

2.3 MORBRDO cost function

MORBRDO cost functionf(µH,σH,α|X)is the linear weighted sum of several objectives.It can be classified to the following four types according to its characteristic:

(1)Smaller-the-better type

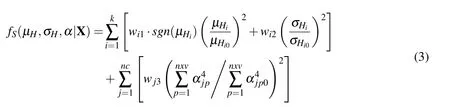
Where µHiand σHiare the mean value and standard deviation of theith performance objective,respectively.Kis the number of the performance objectives; αjis thejth reliability sensitivity coefficient vector,αjpis thepth element of αj;µHi0,σHi0and αjp0are the initial value of µHi,σHiand αjp,respectively.sgn(·)is the sign function;wi1,wi2andwj3are weighting factors to be determined by the designer,they are taken value in[0,1]usually.

(2)Larger-the-better type

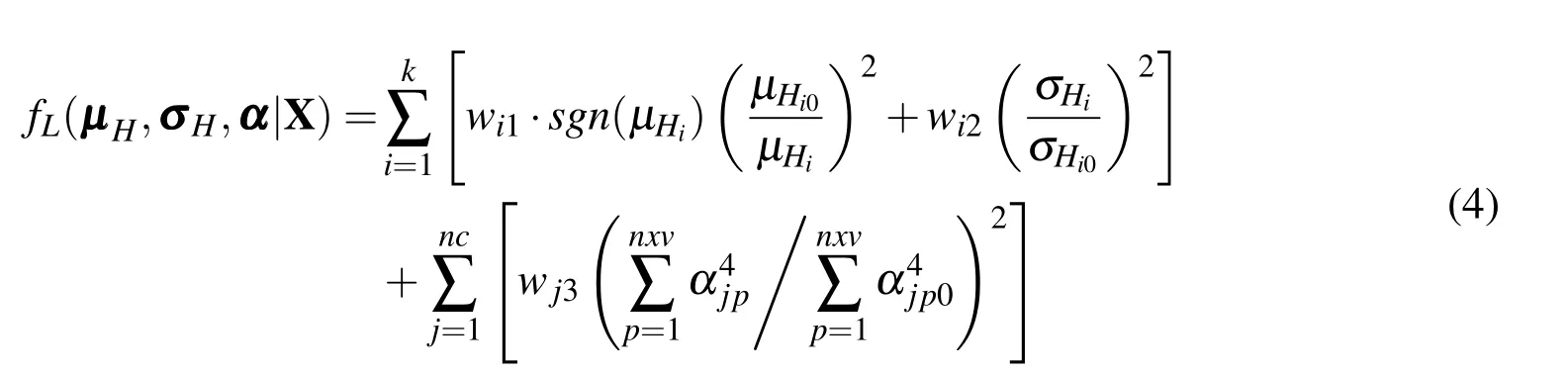
(3)Nominal-the-best type

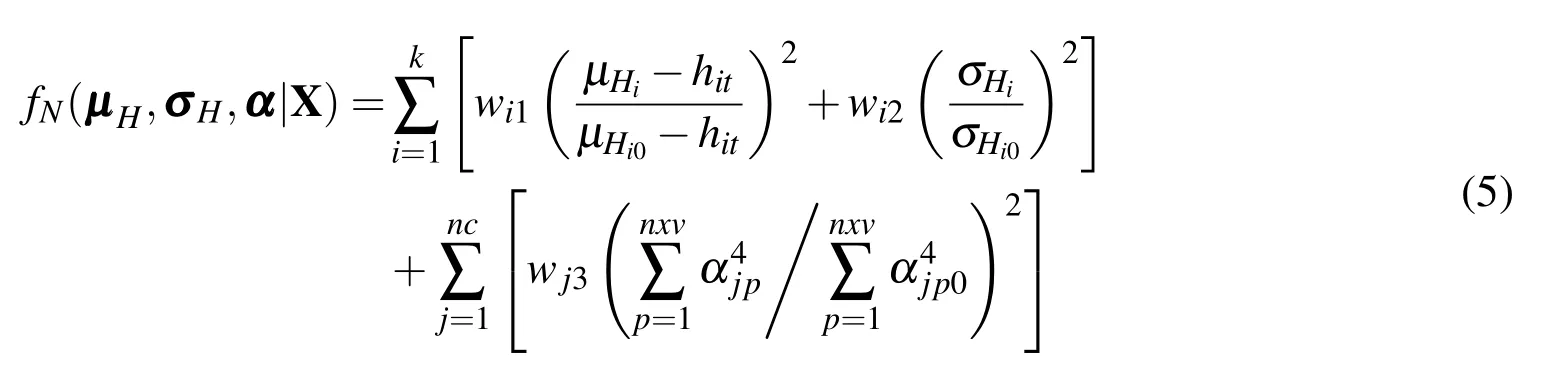
Wherehitand µHi0are the target nominal value and the initial target nominal value of theith performance objective function respectively

(4)Combined type

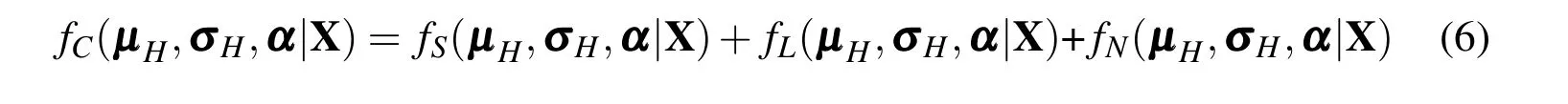
In equations(3)-(6),to reduce the dimensionality problem of multi-objectives,each term is normalized by the initial value µHi0σHi0and αjp0,respectively.The new MORBRDO cost function not only pursuits the optimum of the mean value,but also seeks the minimum values of the standard deviation of the multi-objectives.Moreover,it explores the most robust design of the structural reliability in itself.The weighting factors reflect the preferences of the designer to each objective

3 MORBRDO based on response surface method(RSM)

In practical projects,for structural system with complicated shape and in complex stress condition,it is necessary to get the response values of volume,stress,deformation and inherent frequency by numerical computation method(such as finite element method,FEM).The real function relationships between the responses and the random variables of the structure are so complicate that they can not be obtained,so are the POF and ULSF.In terms of the listed problems,the response surface method(RSM)is an effective method had been developed in recent years.The essence of RSM is to fit an approximate specific function to substitute the real POF or ULSF.And based on the response function,it is relatively easy and feasible to carry out MORBRDO for complicated structures

3.1 The fitting of response functions

The steps to obtain the response function are showed as bellow:

(1)Choose the pure-quadratic polynomial function to fit the relationship between the response and the random variables as the following:

WhereH(X)is the response of the structure,X=(x1,x2,···,xn)is the random variable vector,a,biandciare the coefficients to be determined,nis the number of random variables.

(2)Take the current mean value of variables as the spread point of the response function,compute the response values at the following selected 2n+1 sample points:the mean value point µX=(µx1,...,µxi,...,µxn),2npoints on axis(µx1,...µxi±λσxi,...µxn),where µxiand σxiare the mean value and standard deviation ofxi,respectively.λ is the location parameter of sample points,1≤λ≤3,usually.The 2n+1 values of responses[h1(X),h2(X),...,h2n+1(X)]are obtained by finite element analysis(FEA);

(3)Put the 2n+1 sample points and 2n+1 response value ofH(X)into the Eqn.(7),then a equations set include 2n+1 variables and 2n+1 responses can be gotten.The 2n+1 undetermined coefficientsa,biandcican be obtained conveniently by using the least square method.For convenience,we call the approximate POF and ULSF simulated with the pure-quadratic polynomial functions POF_RSM and ULSF_RSM,respectively.

3.2 Calculation of the mean value and standard deviation of POF_RSM

SupposeH(X)is a certain POF_RSM(such as efficiency,stress,etc),spreadH(X)at the mean value point µXwith Taylor series expansion method and get to the second order items.So:

3.3 Calculation of the reliability and reliability sensitivity coef fi cient based on the ULSF_RSM

(1)Structural reliability index

SupposegX(X)is the ULSF_RSM with respect to a certain failure mode,displaygX(X)as below:

Adopt checking point method to compute the structural reliability index corresponding to Eqn.(11),suppose the checking point isx∗,hence,x∗is located on the ultimate limit state surface,so

SpreadgX(X)at the checking pointx∗with Taylor series expansion method and get to the linear items,so

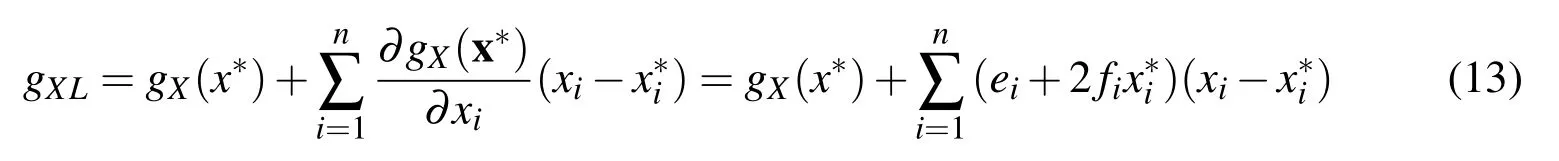
According to the definition of the structural reliability index,the first order reliability index based on checking point method is:

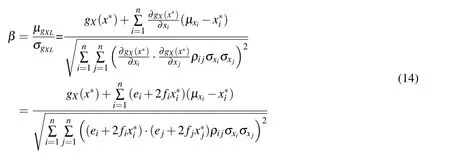
β can be calculated with iteration method.

(2)Reliability sensitivity coefficient

The structural reliability sensitivity coefficient with respect toxiis:

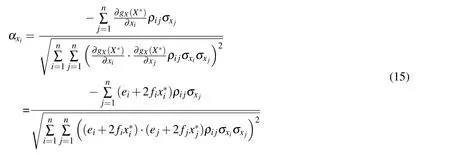
αxiindicates the relative contribution of theith random variable to the standard deviation of ULSF_RSM,and it also reflects its relative influence to the first order reliability index.It is not robust when the influence of a certain variable takes the main part.Hence,it is very natural to hope that each element of αxis relatively equal.

(3)Dealing with non-normal distribution variables Eqn.(14)is appropriate when all the variables of the structure are normal distribution variables.If there are non-normal distribution variables,the mapping transformation method is adopted.Its principle is to map the non-normal distribution variable into standard normal distribution variable in the constraint that the cumulative distribution function(CDF)values of both variables are equal at the checking pointx∗.Supposeyiis a normal distribution variable andxiis a non-normal distribution variable,Φ(yi)andF(xi)are the CDF ofyiandxi,respectively.To carry out the following transformation:

Where ϕ(yi)andfxi(xi)are the probability density function ofyiandxi,respectively.

Put Eqn.(18)into Eqn.(11),the ULSF_RSM with respect to Y:

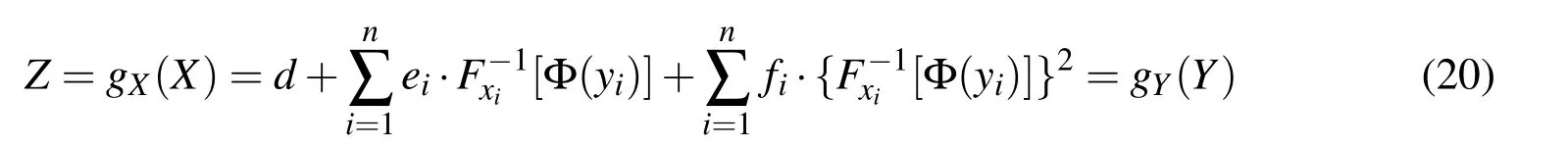
Where,Y=[y1y2···yi···yn],yi∼N(0,1).Then,Eqn.(14)and Eqn.(15)are turned into Eqn.(21)and Eqn.(22)as the following:

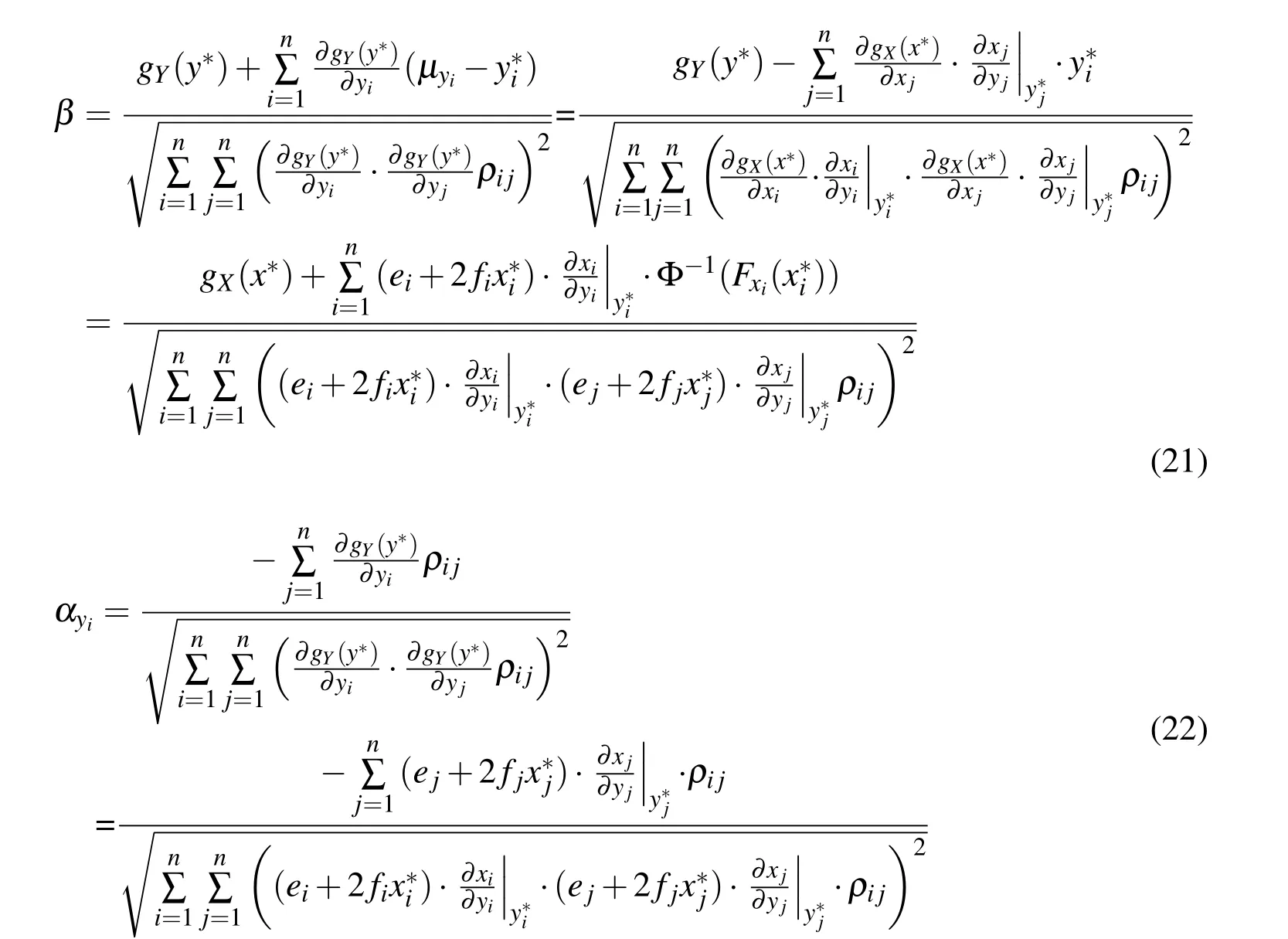
According to Eqn.(19),the below item in Eqn.(21)and Eqn.(22)is deduced:

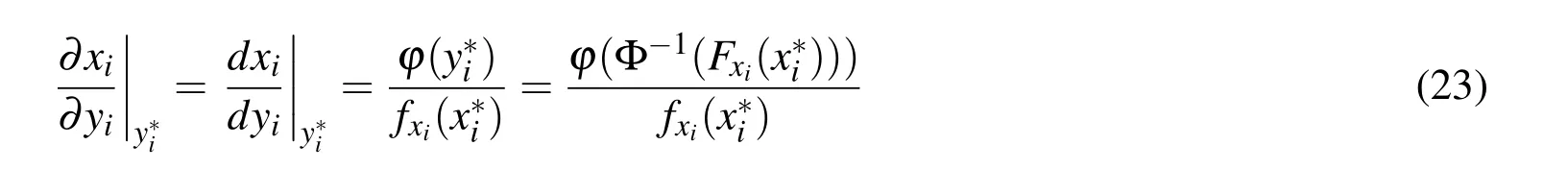
3.4 A new design optimization strategy of MORBRDO

For the structure with unknown ULSF which needs to fit the approximate ULSF with FEM,the main challenge of MORBRDO is the large number of reliability analysis within the optimization process.And the reliability is an iteration process in itself.So,it is a key step to design an efficient optimization strategy for MORBRDO which can guarantee the reliability and in the same time can reduce computational work effectively.Traditional reliability analysis based on RSM and checking point method(TDCRA_RSM)is a double cycle iteration process,as shown in Fig.1.a).In TDCRA_RSM,several iterations(ksupposed)may be needed to get the convergence and reliability index.If the pure-quadratic polynomial function is adopted as the RSM model,2n+1 FEA are needed every time the ULSF_RSM updates,nis the number of variables of the structure.So,k×(2n+1)FEA in total are taken in a TDCRA_RSM in order to get the reliability index under current value of design variables.

In order to enhance the efficiency of reliability analysis,an improved method is proposed,as shown in Fig.1.b).The improved method does not update the ULSF_RSM.Based on the checking point method and the current ULSF_RSM,it ends the reliability analysis when the checking point convergences.We call the improved method the simplified single cycle reliability analysis method based on current ULSF_RSM(SSCRA_RSM).

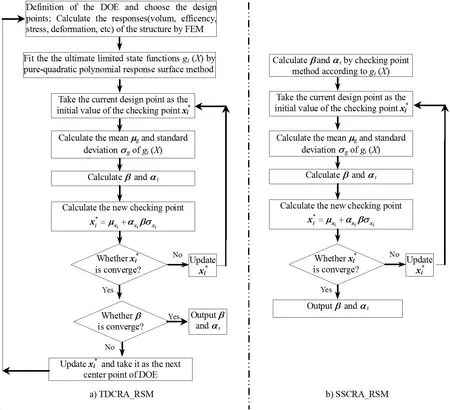
Figure 1:Flow chart of TDCRA_RSM and SSCRA_RSM.

Figure 2:The new design optimization strategy of MORBRDO.

The main distinguish between the TDCRA_RSM and SSCRA_RSM is that the TDCRA_RSM chooses the checking point as the final center point of the ULSF_RSM by iteration.Thus,the computational accuracy of TDCRA_RSM is higher than SSCRA_RSM.However,the computational work is also greatly larger than SSCRA_RSM.The SSCRA_RSM is also based on the checking point method and can deal with correlative and non-normal distribution variables.Although its computational accuracy is lower than TDCRA_RSM,it can satisfy the engineering requirement.The examples followed in this paper will prove this.

Based on the SSCRA_RSM,we proposed a new design optimization strategy of MORBRDO.Its work flow is showed in Fig.2.From the work flow,if the design optimization takesmiterations to gets its convergence,it will takem×(2n+1)FEA for the new strategy.But if the sub-cycle of reliability analysis adopts the TDCRA_RSM,it will takem×k×(2n+1)FEA.It is obviously that the new design optimization strategy of MORBRDO improves the design optimization efficiency remarkably.

The steps of the new MORBRDO methodology are as following:

1)Determine the performance objectives,random variables(include design vari-ables and non-design variables),rang and distributions of the variables;Determine the failure modes of the structure,such as stiffness failure and strength failure;

2)Establish the parameter model of the structure;

3)Adapt the method introduced in section 3.1 of this paper, fit the ULSF_RSM and POF_RSM;

4)Based on the POF_RSM adopt the method introduced in section 3.2 of this paper to calculate the mean values and standard deviations;Based on the ULSF_RSM,adopt the method introduced in section 3.3 of this paper to calculate the reliability index and reliability sensitivity coef fi cient;

5)According to Eqn.(3)∼Eqn.(6),gain the MORBRDO cost function;

6)According to the MORBRDO model in Eqn.(2)of this paper,adopt sequential quadratic programming method to obtain the new design optimization point.

7)Take the new design optimization point as the next iteration point,repeat step 3)∼6)until the cost function value converge to required precision.If more Pareto solutions are needed,adjust the weighting factors and restart the design optimization.

4 Application

4.1 MORBRDO for I-beam structure

To obtain the minimum sectional area of the I-beam structure,as shown in the Fig.3,under the concentrated forceP.The constraints are as the following:vertical distortion less than 0.3mm;bending stress less than 160Mpa.Eis elasticity modulus of the beam material.The variables of the I-beam structure and their statistical properties and correlation coefficients are shown in Tab.1.Please redesign the sizes of I-beam structure with MORBRDO method.

Analysis:In terms of the I-beam structure,the analytic solution of MORBRDO can be obtained.So this example can be used to testify the feasibility and validity of the method proposed in this paper.

According to the purpose of the problem,the POF is the sectional area as following:

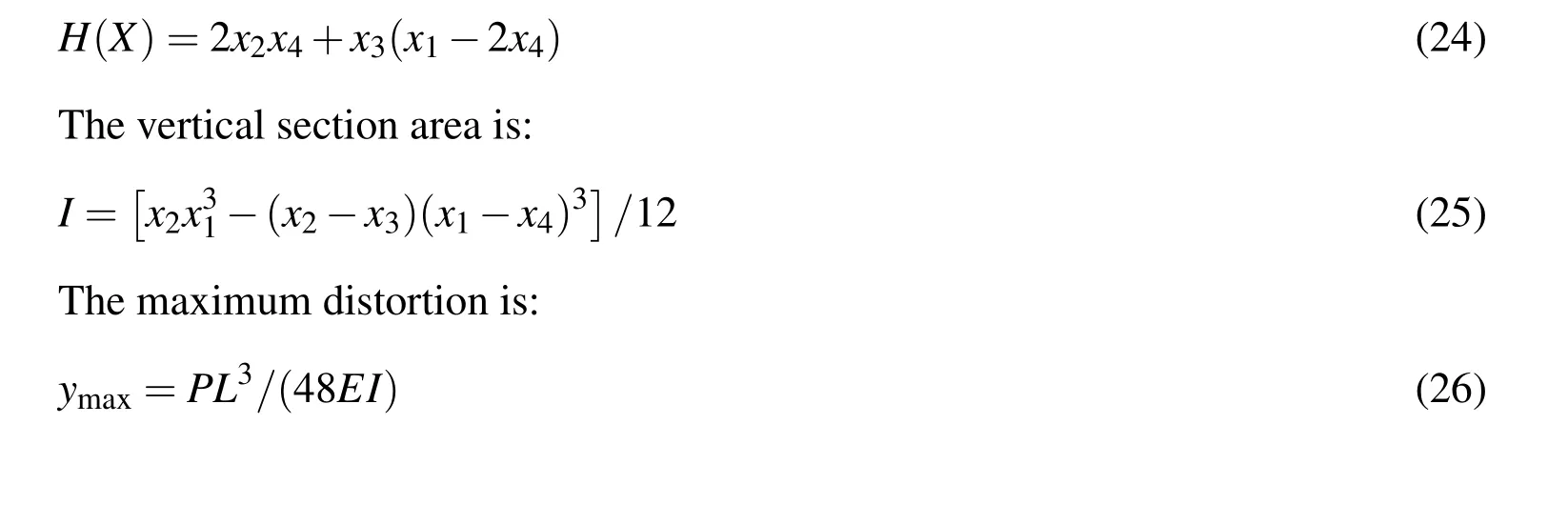
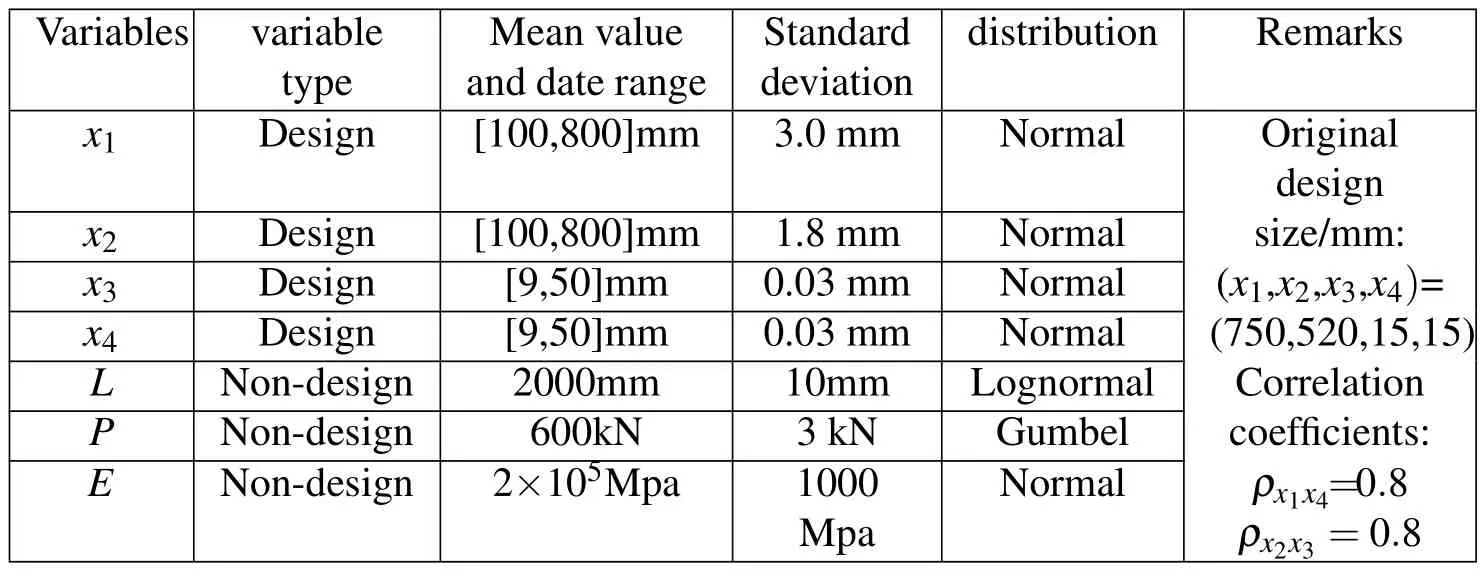
Table 1:Types,ranges,statistical properties and correlation coefficients of random variables of I-beam structure.

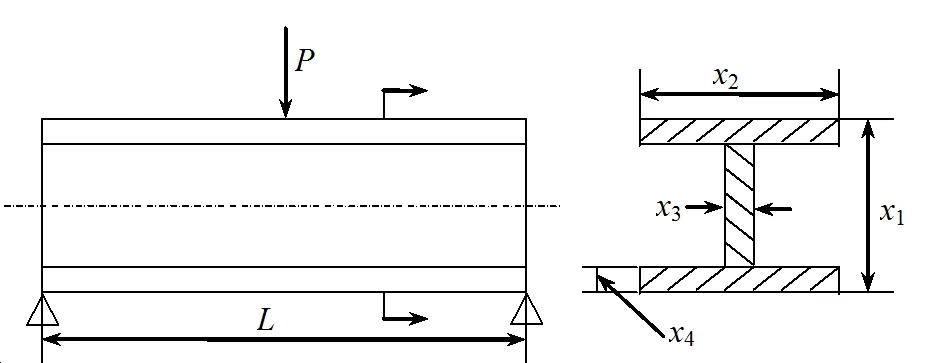
Figure 3:Sketch map of I-beam structure.

TDO and MORBRDO had been implemented to the I-beam structure.The optimization results are shown in Tab.2.Where βtis the optimum result of structural system index and βM_Cis the optimum result with Monte-Carlo method,which had taken the advantage of the analytic equations of Eqn.(24)∼Eqn.(30).

According to Tab.2,the mean value and standard deviation of the performance objective(sectional area of the beam)decreased remarkably after MORBRDO compared with the initial design.The structural reliability meets the requirement.When compared the MORBRDO with the Monte-Carlo method,which are regarded as the most accurate one,the differences of the results are small.So,the MORBRDO are accurate and reliable.Different weighting factors caused different design results and revealed the preferences of the weighting factors to the objectives.In this paper,the MORBRDO cost 165 FEA in the whole 11 iterations.If the TDCRA_RSM which had been introduced in section 3.4 in this paper is adopted,it will cost 825 FEA.But the optimization results will be almost the same as the results in Tab.2.

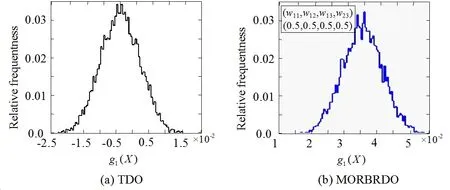
Figure 4:Statistics histogram of g1(X).

Statistics histograms ofg1(X)after designed by TDO and MORBRDO respectively are showed in Fig.4.After TDO,the optimum cross-sectional area of the beam is the minimum.So,it could utmost to reduce the cost of raw materials for TDO.But,because of the randomness of the variables,the mean value ofg1(X)is about zero,the optimum point is near the border of the failure surface and the structural reliability is just about 50%;After MORBRDO,however,the optimum point is far away from the border of the failure surface and the structural reliability is about Φ(6).

4.2 MORBRDO for the pressure vessel

Pressure vessel is a kind of important equipment being widely used in engineering,to design a cylindrical pressure vessel with standard elliptical head(as shown in Fig.5).The total volume is 80m3and the pressure that the vessel bears isPc.The vessel is made of 16 Mn Rsteel whose allowable stress isSσand welded joint coefficient φ is 0.85.The length-diameter ratio constraint is 3≤L/D≤20.Types,ranges,statistical properties and correlation coefficients of random variables and other parameters of the pressure vessel are shown in Tab.3.Please design the sizes of pressure vessel with MORBRDO method.

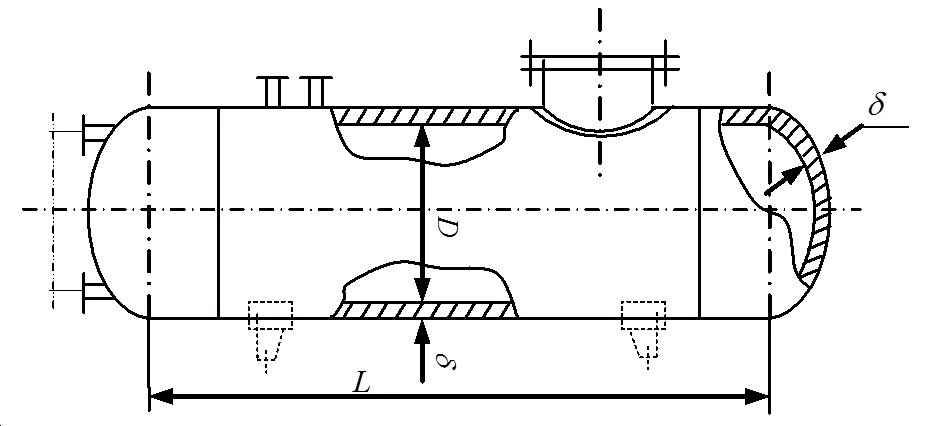
Figure 5:Sketch map of pressure vessel.

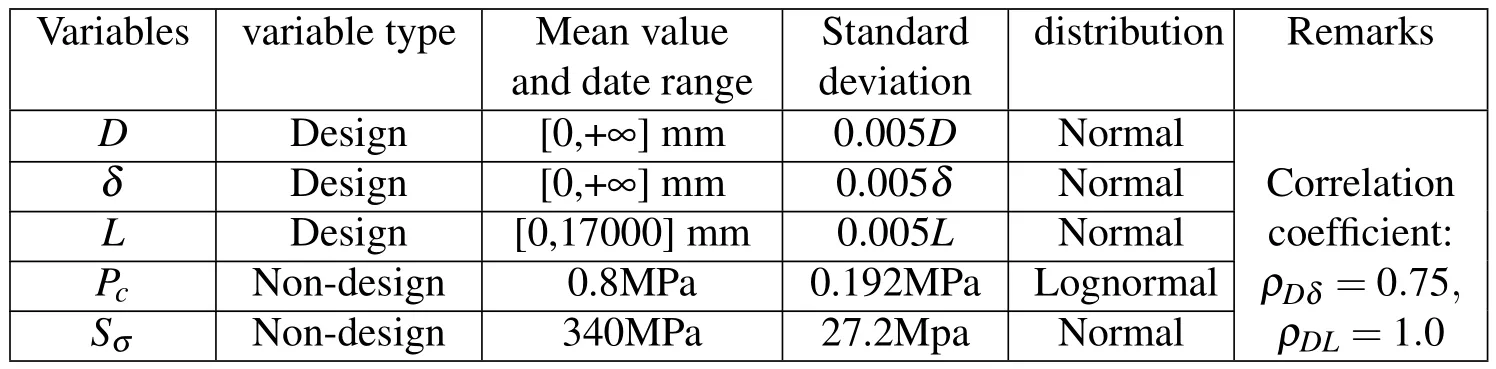
Table 3:Types,ranges,statistical properties of the random variables of pressure vessel.

Analysis:Under internal pressure,the maximum stress is at the circumferential direction and the apex of the standard elliptical head.And the value is:

The POF(the total mass)is:

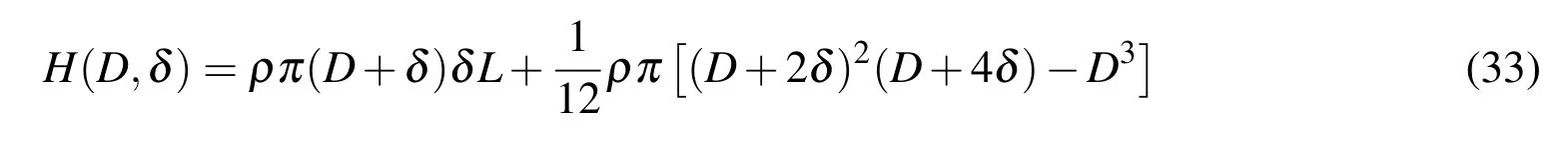
Where ρ is the material density of the vessel,ρ =7850Kg/m3.

The total volume

The smaller-the-better type cost function in Eqn.(3)is chosen for the MORBRDO of the pressure vessel.The optimization results are shown in Tab.4.After MORBRDO,the structural reliability reached the target value,the inner diameterDand the thickness δ of the pressure vessel were decreased,but the length was increased.

4.3 MORBRDO for the turbine blade model lines

The turbine blade is the key parts of the gas turbine,and the aerodynamic efficiency,structural strength and intrinsic frequency,etc,are closely connected with blade model lines,see Nikita and Keane(2011);PENG and YANG.(2012).In terms of the guide blade,the maximum aerodynamic efficiency is expected.For the rotating blade,because it is rotating under the high-speed and high temperature currents of gas,it bears very complicated stress.Therefore,it is necessary to design its model lines with MORBRDO method.

4.3.1Parameter modeling of turbine blade model line

Taking the advantage of the basic geometry characteristic parameters of the turbine blade model line such as the blade widthB,setting angle γp,radius of leading edger1and trailing edger2, flow inlet angle β1and flow outlet angle β2wedge angle of leading edge ϕ1and trailing edge ϕ2,we describe the blade model lines with three cubed Bezier curve,as shown in Fig.6.

According to the coordinates ofG,U1,U2,D,the equations of the suction side line curve with respect to three cubed Bezier curve are:

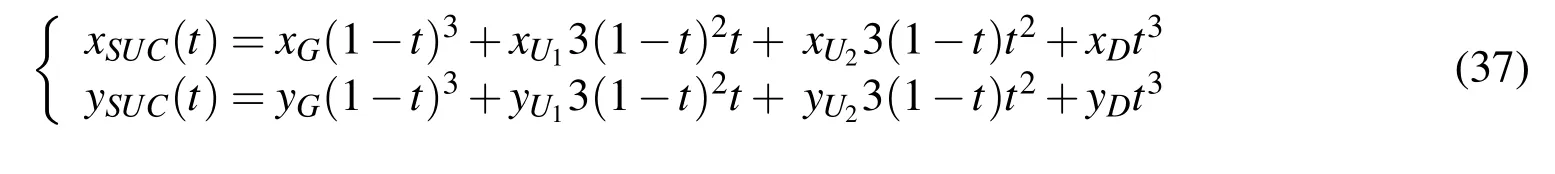
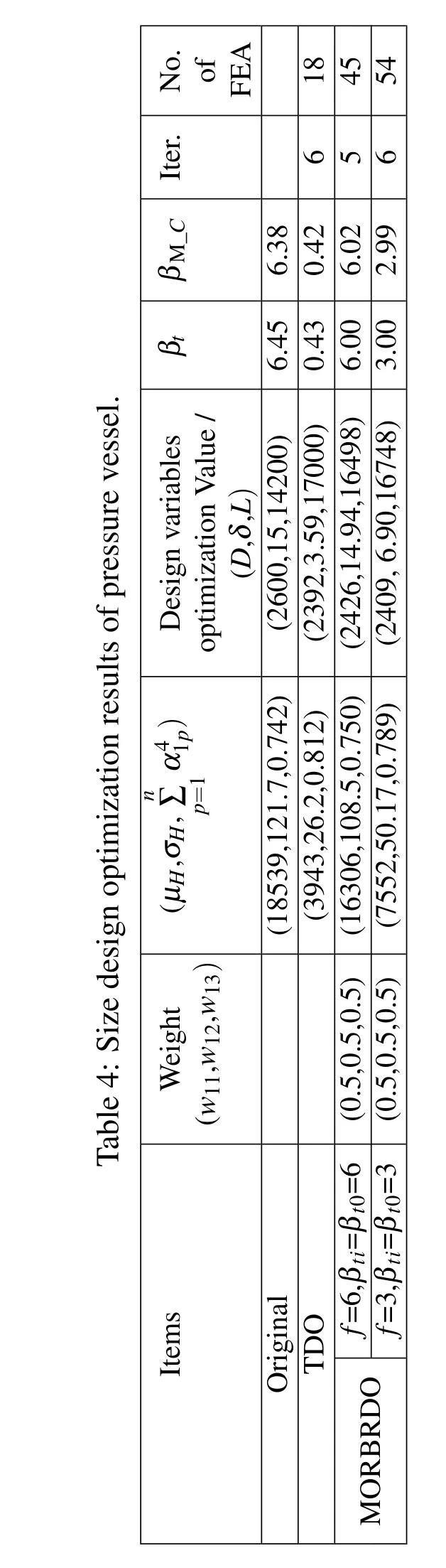
Figure 6:Description of blade model lines with three cubed Bezier curve.

Where 0≤t≤1,and the pressure side line equations could be obtained in the similar way.The coordinates ofG,U1,U2,Dand the detailed equations of the model lines expressed by the basic geometry characteristic parameters of the turbine blade had been deduced by the authors,see PENG and YANG(2012).

4.3.2Parameter modeling of blade flow field and heat- fluid-solid coupling analysis

Based on the parameter equation of the blade model line,the parameter models of the blade and flow field are established with Pro/Engineering software.The parameter models under original design are shown in Fig.6.

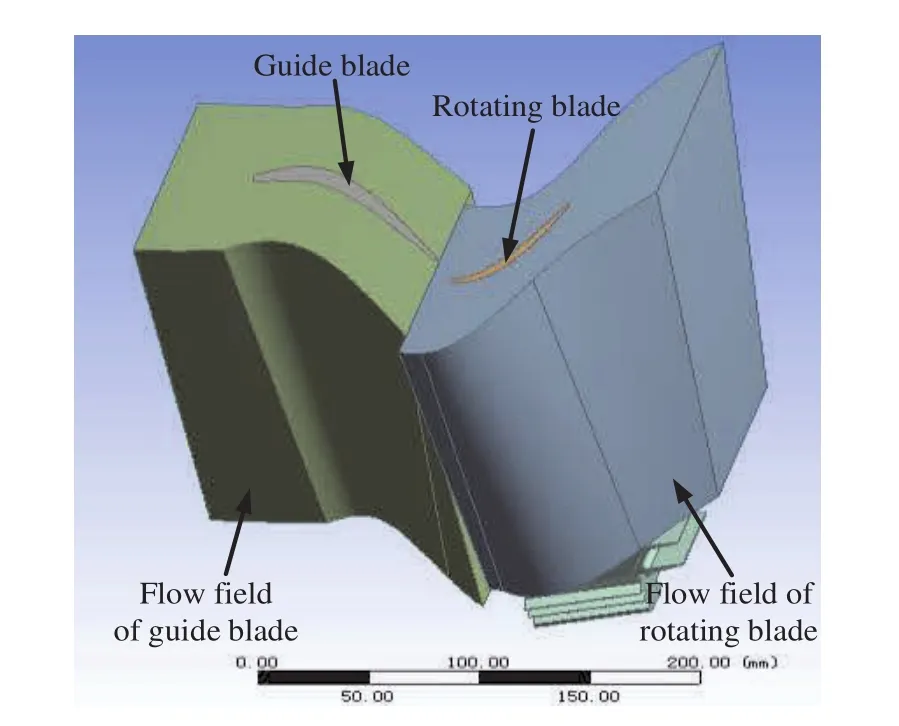
Figure 7:Blade and flow field models.

In order to obtain the aerodynamic efficiency,stress and deformation,etc of the blade accurately,the heat- fluid-solid coupling analysis is adopted.The coupling analysis is accomplished with Ansys Workbench 12.1.The flow field analysis chooses the shear stress transport(SST)as the turbulence model.According to the dates of the stand tests and the actual working records of the turbine under design working condition,the loads inflicted to the flow field analysis are as the following:to inflict the flow field inlet with mass flow rate and average temperature;to inflict the flow field outlet with average static pressure;stationary inertial frame is chosen for the guide blade flow field;the non-inertial frame which is rotating around the main shaft of the turbine at a certain angular velocity is chosen for the rotating flow field;in each reference frame,the flow field boundary is heat insulation,solid wall,zero speed condition without slip;choose the CFX frozen rotor model to transfer the calculation dates between the guide blade flow field and the rotating blade flow field;adopt general grid interface(GGI)method to map the dates.The flow analysis obtains the distribution of the temperature,pressure and gas velocity of the flow field and blade surface.And then the aerodynamic efficiency of the blade is calculated.After,the temperature and pressure of the blade surface of the flow analysis together with the angular velocity are conducted as loads of the stress analysis.Then the stress,deformation and intrinsic frequency,etc are obtained by stress analysis.Partial results of the heat- fluid-solid coupling analysis of the blade are shown in Fig.8-Fig.10.

4.3.3MORBRDO of blade model lines

(1)Choice of POF

For both of the guide blade and rotating blade,we choose the aerodynamic efficiency and the blade volume as the main POF.

MORBRDO cost function:The aerodynamic efficiency is always expected to increase.But the volume is expected to decrease,so the combined type in Eqn.(6)is chosen for the turbine blade model lines MORBRDO.

Because the guide blade is stationary,so the stress and deformation are much smaller than the rotating blade.In this paper,we mainly take the rotating blade into consideration and carry out the stress and reliability analyses to it.

(2)Probability constraints of rotating blade

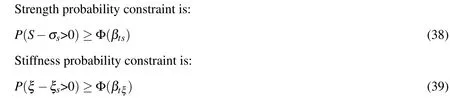
Figure 8:The pressure,temperature,Mach number and turbulence kinetic energy distributions of the flow field at 10%,50%and 90%blade height.

Resonance frequency probability constraint is:

WhereS,ξ andFare the maximum stress,maximum deformation and natural frequency of the rotating blade under design working condition,respectively.ξsis the allowed deformation;σsis the yield strength of blade at the working temperature.FIis the rotational frequency of the turbine,kis the number of even-distributed excitation sources,usually onlyk=1 andk=2 are being taking into consideration.βts,βtξgand βtFare the target reliability indexes with respect to strength,stiffness and vibration failure modes respectively.

Figure 9:Pressure changing with the blade model line at the 50%blade height.

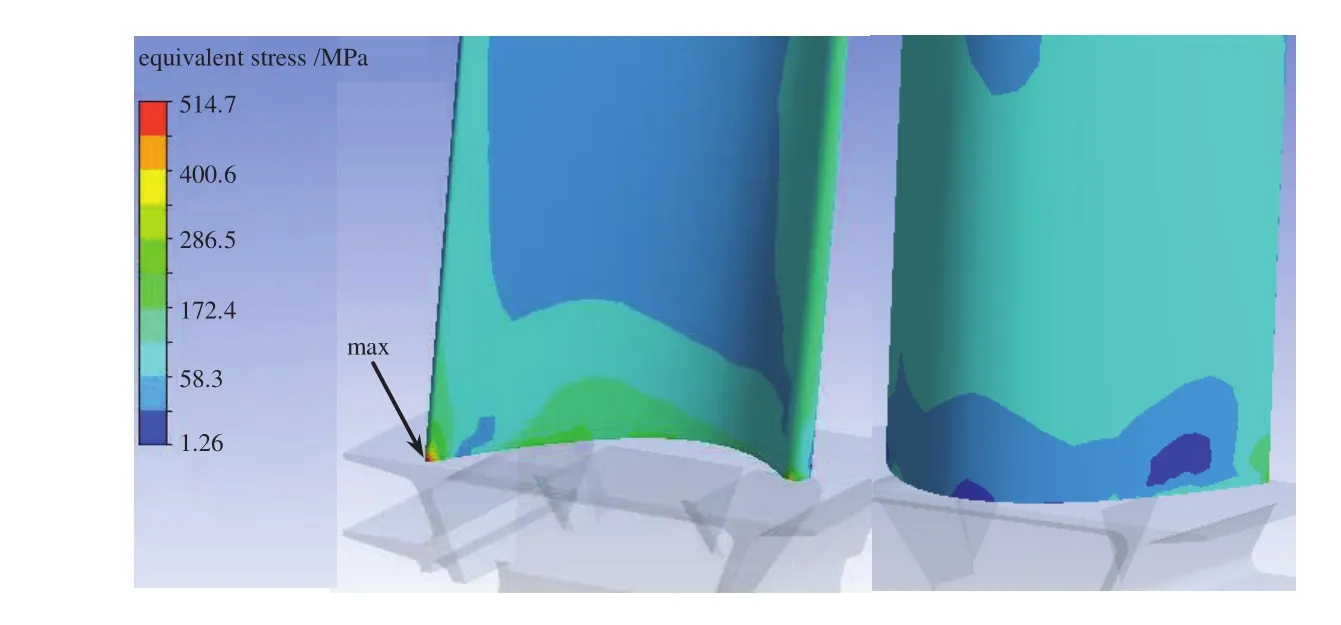
Figure 10:Equivalent stress distribution of rotating blade.

(3)MORBRDO cost function for turbine blade 1.for turbine guide blade,the MORBRDO cost function is 2.for turbine rotating blade,the MORBRDO cost function is

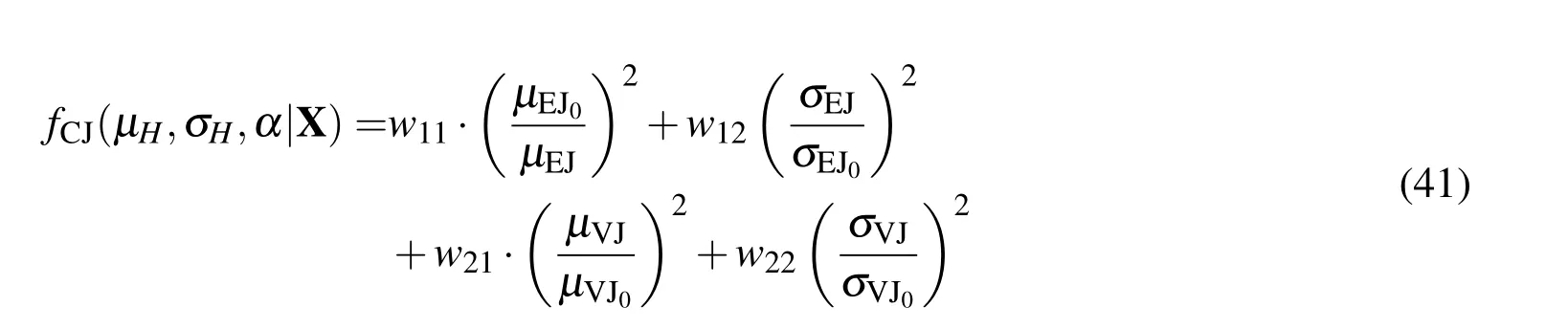
In Eqn.(41)and Eqn.(42),µEJ,µMJ,µED and µMD are the mean value of the aerodynamic efficiency of guide blade,volume of guide blade,efficiency of rotating blade and volume of rotating blade,respectively. σEJ,σMJ,σED and σMD are the standard deviation of the aerodynamic efficiency of guide blade,volume of guide blade,efficiency of rotating blade and volume of rotating blade,respectively.µEJ0is the value of µEJ when the blade is in initial design,so as to other items.The last item in Eqn.(42)is the objective of the reliability sensitivity coefficient with respect to Eqn.(38)-Eqn.(40).

(4)Variables definition

In MORBRDO,the design parameters are regarded as random variables.Moreover,the non-design random variables also must be taken into consideration.In terms of the turbine blade,the non-design variables and other parameters are shown in Tab.5.The design variables and their ranges are shown in Tab.6.Where,Minlet,Tinlet,andPoutletare the mass flow rate,inlet average temperature and outlet average static pressure of the flow field,respectively.

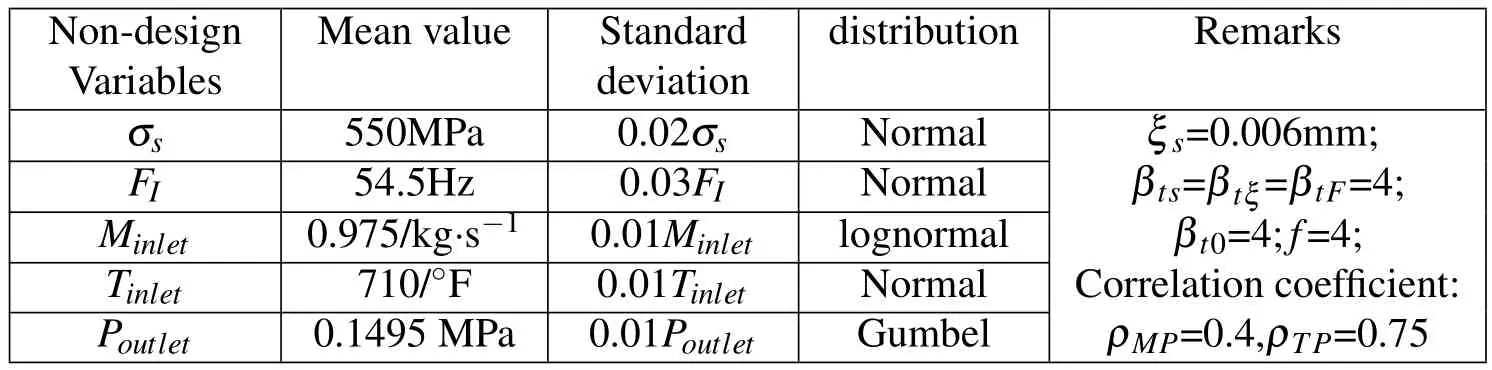
Table5:Statistic parameters and distributions of the non-design variables of turbine blade.

The weighting factorswijreflects the preference of the designer to each objective.For turbine blade,wijis chosen in four cases,as shown in Tab.6.

According to the sensitivity analysis based on DOE and FEA,six parameters including β1,β2,ϕ1,ϕ2,R1andR2,as shown in Tab.7,which have the major influences on the aerodynamic efficiency and stress of the blade are chosen to be optimized.

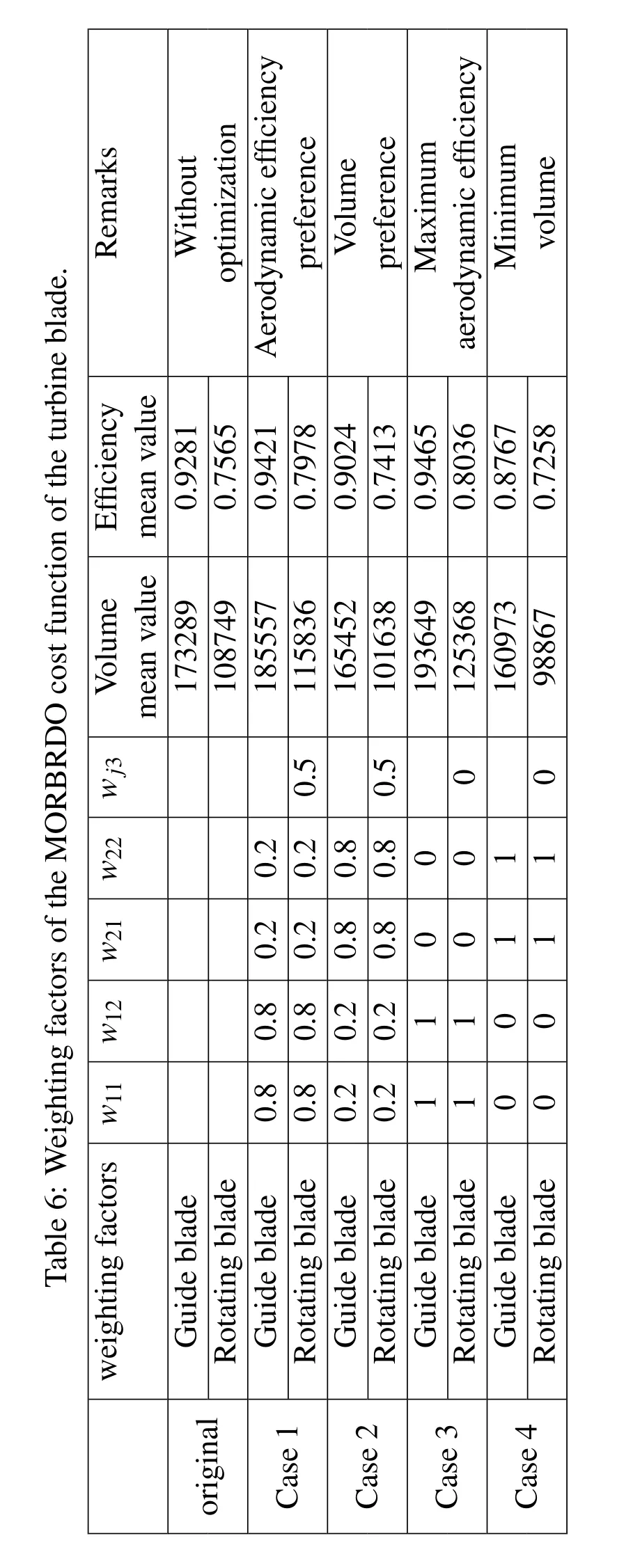
(5)MORBRDO results

According to the new design optimization strategy of MORBRDO in section 3.4,we have achieved the design optimization with respect to the above four cases in Tab.6.Take the case 1 for instance,the whole MORBRDO takes 9 iterations(350 hours in total)to achieve optimization.The optimum value of the design variables and performance objectives are shown in Tab.7∼Tab.9.After MORBRDO,the aerodynamic efficiencies of the guide blade and the rotating blade are increased by 1.5%and 5.4%respectively;the maximum stress and the maximum deformation of the rotating blade are decreased by 16.8%and 8.5%respectively;and the standard deviations of the above performance objectives are decreased too,so the robustness of the blade is increased.What’s more,the structural system reliability reached 99.99%,but before MORBRDO it is only 89.4%.Fig.11 shows the comparing of turbine blade model line figures before and after MORBRDO.Fig.11∼Fig.13 show the comparing of the turbulence kinetic energy changing along with the blade model line at the 10%,50%and 90%blade height before and after MORBRDO,respectively.The turbulence kinetic energy reflects the loss of kinetic energy of the blade.So Fig.12∼Fig.14 show that,after MORBRDO,the maximum loss of kinetic energy of the blade surface at the 10%,50%and 90%blade height decrease by 14.9%,11.1%and 17.6%respectively.However,the means and standard deviations of the blade volumes increased a little,so the cost of the blade material would be increase finally.

For turbine blade,the aerodynamic efficiency and the volume would not get the optimum at the same time,as shown in Fig.15.The mean value of the aerodynamic efficiency and volume of the guide blade and rotating blade in Case 1 to Case 4 are shown in Tab.6 and Fig.15.The results show that the original design is a feasible design but not a Pareto solution.By changing the weighting factors and redesign,we can get the Pareto frontier of the turbine blade model line design optimization solutions,as shown in Fig.15.

Therefore,MORBRDO can ensure the structural reliability and enhance the robustness of the structure on the one hand;but on the other hand,it may sacrifice some other desirable performances,such as the costs,time,quality,etc.So the MORBRDO could be regarded as a trade-off compromise design method.

5 Conclusions

In this paper,a new MORBRDO model and a new design optimization strategy were proposed.Based on the pure-quadratic polynomial function model,the reliability calculation equations with non-normal distribution variables,the mean value and standard deviation equations of performance objectives were deduced.The I-beam structure,a pressure vessel and the turbine blade model lines were introduced to testify the MORBRDO methodology.The main concluding remarks could be summarized as below:

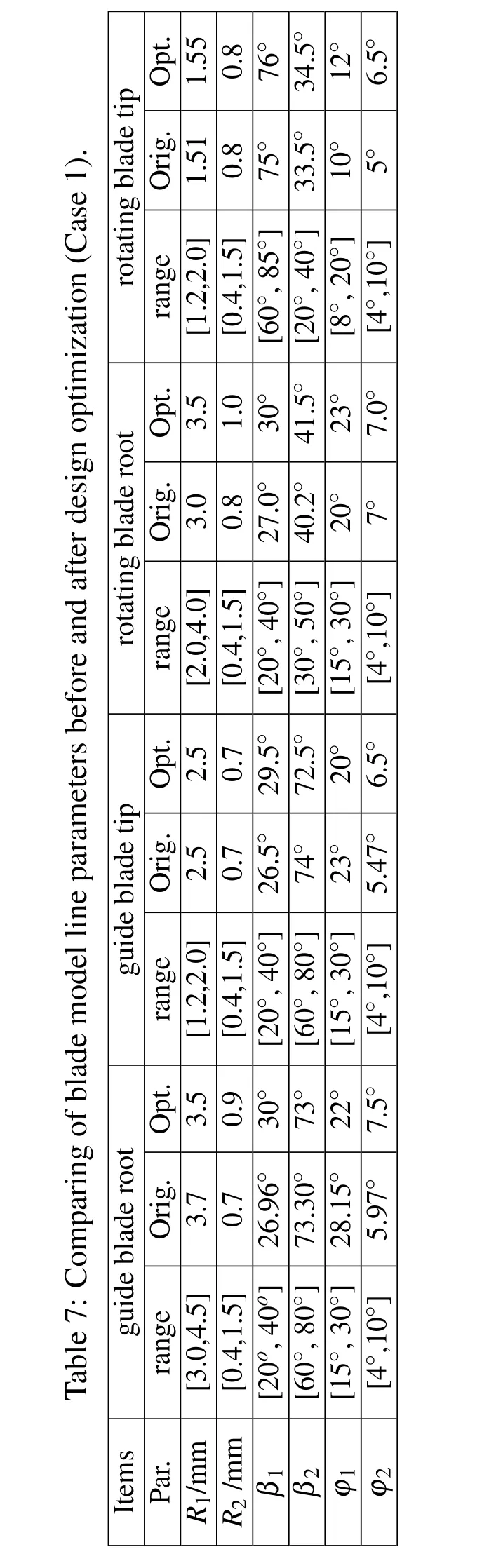
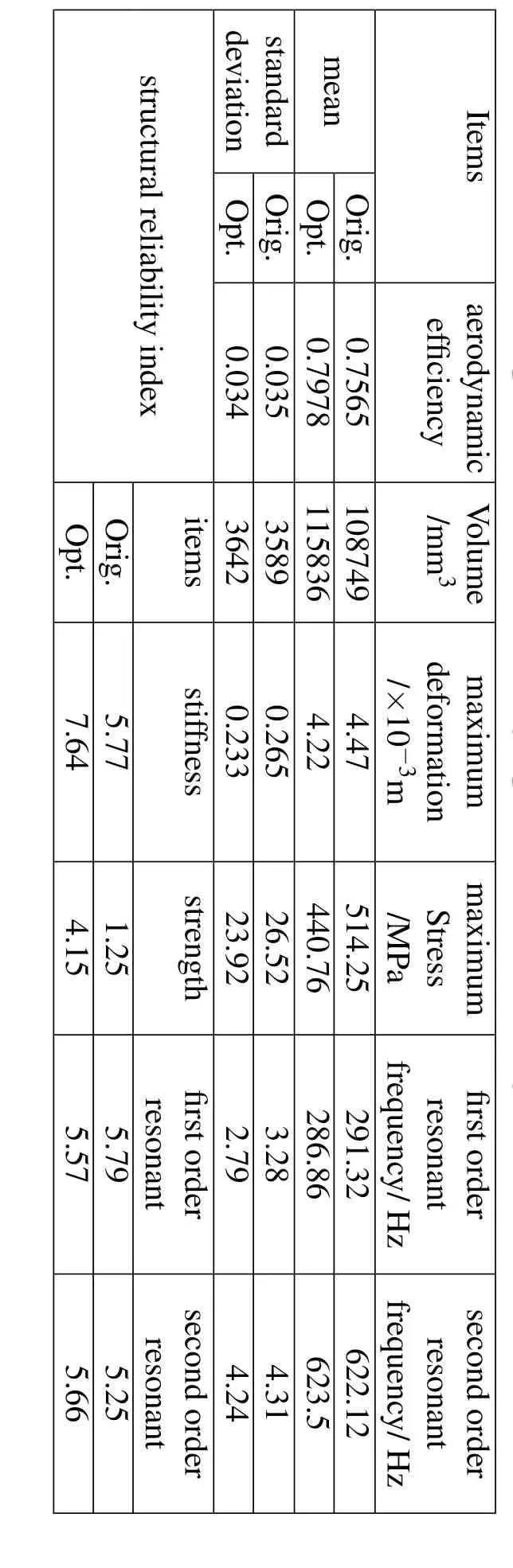
Table 8:Optimization results of target parameters of rotating blade(Case 1)

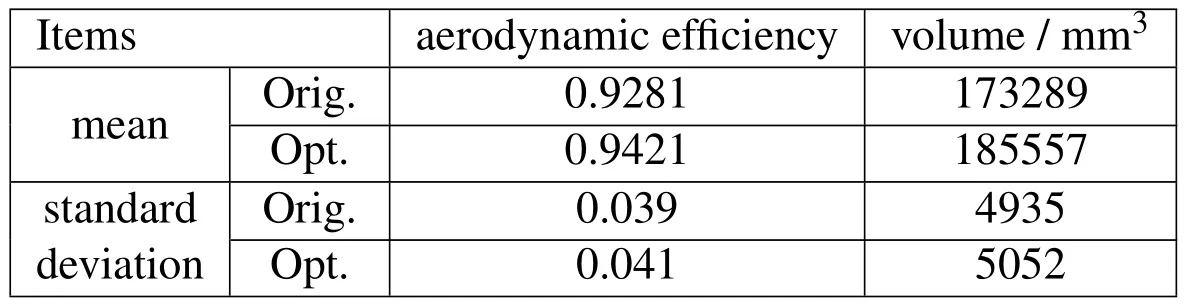
Table 9:Optimization results of target parameters of guiding blade(Case 1).

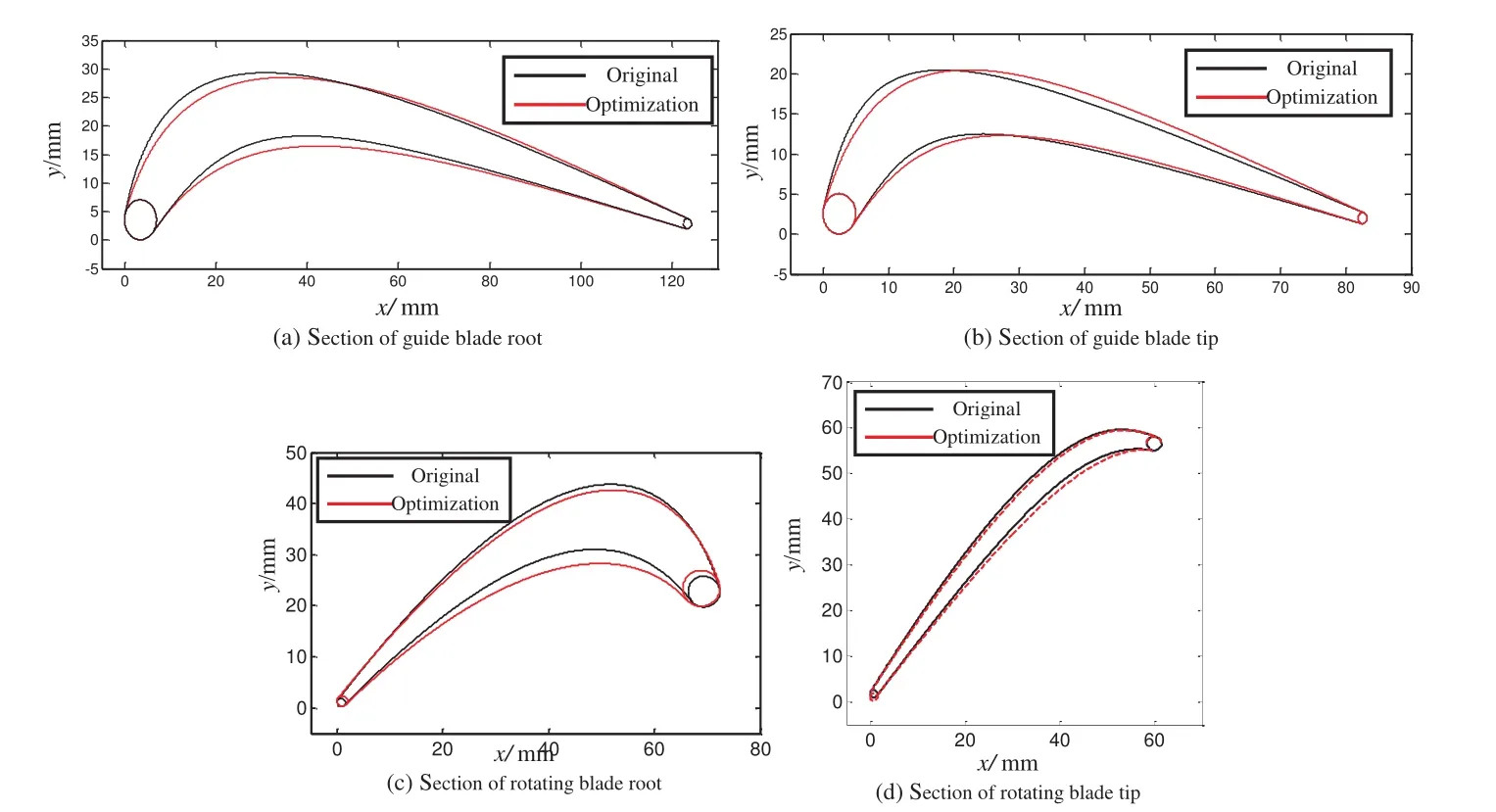
Figure 11:Comparing of turbine blade model line figures before and after MORBRDO(Case 1).

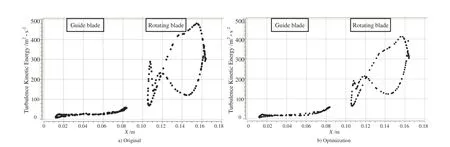
Figure 12:Compare of the turbulence kinetic energy changing along with the blade model line at the 10%blade height before and after MORBRDO(Case 1)

Figure 13:Compare of the turbulence kinetic energy changing along with the blade model line at the 50%blade height before and after MORBRDO(Case 1).

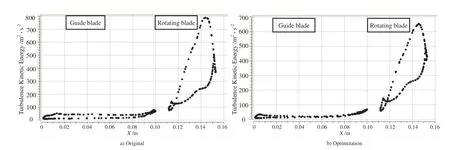
Figure 14:Compare of the turbulence kinetic energy changing along with the blade model line at the 90%blade height before and after MORBRDO(Case 1).

(1)The new MORBRDO model takes advantages of the multi-objective robustness,the reliability sensitivity robustness and the six sigma robustness design idea.It considers the multi-objectives and multi-failure modes simultaneously,ensures the system reliability and enhances the robustness of the structure.

(2)In terms of the structure with unknown ULSF and POF,the new MORBRDO model adopts the pure-quadratic polynomial function to obtain approximate ULSF and POF.It makes the design optimization feasible and relatively easy to implement.

(3)The new design optimization strategy does not update the ULSF_RSM,so it reduces computational work of FEA and improves optimization efficiency remarkably.

(4)Two real projects of I-beam structure and pressure vessel with analytic solutions had been introduced and had verified the accuracy and feasibility of the new MORBRDO methodology.Then the new methodology was also adopted to redesign the turbine blade model lines.And the Pareto frontier of the turbine model line MORBRDO solutions is obtained.So it could be inferred that the new MORBRDO methodology could be applied to the complicated structures.

(5)For the MORBRDO,in order to improve the robustness and guarantee the reliability of the structure,it may sacrifice some other desirable performances,such as manufacturing costs,time,etc.In actual engineering,the designer can adjust the target reliability index,the robustness level or the weighting factors to trade off between the quality enhancement and the costs decrease.

Acknowledgement:We would like to express our appreciation to the“Innovation Funds for PhD of Chinese Naval University of Engineering”.This work was also partly supported by the New Century National Excellent Talents Program through the Ministry of Human Resource and Social Security of China.We are also pleased to acknowledge the support of Professor S.N.Atluri of University of California,Irvine.

Adam,M.;Tadeusz U.(2012):Reliability and performance-based robust design optimization of MEMS structures considering technological uncertainties.Mechanical Systems and Signal Processing,vol.32,pp.44-58.

Alois,S.;Hans,T.(2001):Methods for dimension reduction and their application in nonlinear dynamics.International Journal of Solids and Structures,vol.38,pp.21312147.

Andy,J.K.(2009):Comparison of several optimization strategies for robust turbine blade design.Journal of Propulsion and Power,vol.25,no.5,pp.1092-1099.

Besharati,B.;Luo,L.;Azarm,S.(2006):Multi-objective single product robust optimization:an integrated design and marketing approach.ASME J.Mech.Des.,vol.128,pp.884-892.

Cho,J.Y.;Oh M.H.(2010):Sequential approximate optimization procedure based on sample-reusable moving least squares meta-model and its application to design optimizations.CMES:Computer Modeling in Engineering&Sciences,vol.66,no.3,pp.187-213.

Darian,R.;Alexander,S.;Jan,V.V.(2009):Robust multi-objective optimization for water distribution system design using a meta-metaheuristic.Intl.Trans.In Op.Res.,vol.16,pp.595-626.

Du,X.P.;Chen,W.(2004):Sequential optimization and reliability assessment method for efficient probabilistic design.ASME J.Mech.Des.,vol.126,pp.225-233.

Dubey,A.K.;Yadava,V.(2008):Robust parameter design and multi-objective optimization of laser beam cutting for aluminium alloy sheet.Int J Adv Manuf Technol,vol.38,pp.268-277.

Hasofor,A.M.;Lind,N.C.(1974):Exact and invariant second-moment code format.Journal of the Engineering Mechanics Division,ASEM,vol.100(EM1),pp.111-121.

Kaminski,M.M.;Szafran,J.(2012):Stochastic finite element analysis and reliability of steel telecommunication towers.CMES:Computer Modeling in Engineering&Sciences,vol.83,no.2,pp.143-167.

Kipouros,T.;Jaeggi,D.M.;Dawes,W.N.et al.(2008):Insight into highquality aerodynamic design spaces through multi-objective optimization.CMES:Computer Modeling in Engineering&Sciences,vol.37,no.1,pp.1-23.

Koch,P.N.;Yang,R.J.;Gu,L.(2004):Design for six sigma through robust optimization.Struct Multidisc Optim,vol.26,pp.235-248.

Lee,I.;Choia,K.K.;Du,L.(2008):Dimension reduction method for reliability-based robust design optimization.Computers&Structures,vol.86,pp.1550-1562.

Li,M.;Azarm,S.;Boyars,A.(2006):A new deterministic approach using sensitivity region measures for multi-objective robust and feasibility robust design optimization.ASME J.Mech.Des.,vol.128,pp.874-883.

Li,S.Z.;Zhao,F.;Ni,Q.J.(2013):Multiobjective optimization for ship hull form design using SBD technique.CMES:Computer Modeling in Engineering&Sciences,vol.92,no.2,pp.123-149.

Lu,H.;Zhang,Y.M.(2011):Reliability-based robust design for structural system with multiple failure modes.Mechanics Based Design of Structures and Machines,Vol.39,pp.420-440.

Luo Z.;Zhang N.;Wang,Y.(2012):A physically meaningful level set method for topology optimization of structures.CMES:Computer Modeling in Engineering&Sciences,vol.83,no.1,pp.73-96.

Nikita,T.;Keane,A.J.;Nair,P.B.(2011):Robust design of turbine blades against manufacturing variability.Int.J.Reliability and Safety,vol.5,no.3,pp.420-435.

Om,P.Y.;Sunil,S.B.;Ajay,R.(2010):Reliability-based robust design optimization:A Multi-objective framework using hybrid quality loss function.Quality and Reliability Engineering International,vol.26,pp.27-41.

PENG,M.L.;YANG,Z.C.;CAO,Y.Y.et al.(2012):Parameter modeling of turbine blade model line construction based on bezier curve and particle swarm optimization algorithm.Chinese Proceedings of the CSEE,vol.32,no.12,pp.101-108.

Rachwitz,R.;Fiessler,B.(1978):Structural reliability under combined random load sequences.Computers&Structures,vol.9,no.5,pp.489-494.

Rahman,S.;Xu,H.(2004):A univariate dimension-reduction method for multidimensional integration in stochastic mechanics.Probabilistic Engineering Mechanics,vol.19,pp.393408.

Razzaq,M.;Tsotskas,C.;Turek,S.;Kipouros,T.;Savill,M.;Hron,J.(2013):Multi-objective optimization of a fluid structure interaction benchmarking.CMES:Computer Modeling in Engineering&Sciences,vol.90,no.4,pp.303-337.

Rajagopal,S.;Ranjan,G.(2011):Multidisciplinary design optimization of long endurance unmanned aerial vehicle wing.CMES:Computer Modeling in Engineering&Sciences,vol.81,no.1,pp.1-34.

Santos,S.R.;Matioli,L.C.;Beck,A.T.(2012):New optimization algorithms for structural reliability analysis.CMES:Computer Modeling in Engineering&Sciences,vol.83,no.1,pp.23-55.

Shimoyama,K.(2008):Development of multi-objective six-sigma approach for roust design optimization.Journal of aerospace computing,information and communication,vol.5,pp.215-233.

Shun,M.;Suzuki,H.;Takahisa,l.et al.(2011):Robust parameter design using a supersaturated design for a response surface model.Quality and ReliabilityEngineering International,vol.27,pp.541-554.

Trapani,G.;Kipouros,T.;Savill,A.M.(2012):The design of multi-element airfoils through multi-objective optimization techniques.CMES:Computer Modeling in Engineering&Sciences,vol.88,no.2,pp.107-138.

Wang,J.G.;Zhang,J.F.;Du,X.P.(2011):Hybrid dimension reduction for mechanism reliability analysis with random joint clearances.Mechanism and Machine Theory,vol.46,pp.1396-1410.

Wang,L.P.(2002):An effective method for probabilistic and robust design with non-normal distributions.43rdAIAA/ASME/ASCE/AHS/ASC Structures,Structural Dynamics,and Materials Con,2002,Denver,Colorado,pp.1-13.

Yang,Z.C.;Sun,W.C.(2013):A set-based method for structural eigenvalue analysis using Kriging model and PSO algorithm.CMES:Computer Modeling in Engineering&Sciences,vol.92,no.2,pp.193-212

Yu,H.;Gillot,F.;Ichchou,M.(2013):Reliability based robust design optimization for tuned mass damper in passive vibration control of deterministic/uncertain structures.Journal of Sound and Vibration,vol.332,pp.2222-2238.

Zhen,H.;Zhu,P.F.;Wang,J.et al.(2009):Robust multi-response parameter design based on RSM.The Asian Journal on Quality,vol.10,no.3,pp.1-11.

Zhou,X.J.;Ma,Y.Z.;Tu,Y.L.et al.(2013):Ensemble of surrogates for dual response surface modeling in robust parameter design.Qual.Reliab.Engng.Int.,vol.29,pp.173-197.