基于卡尔曼滤波的基坑变形监测数据处理及分析

李增强 宋 杰

（1.山东鲁能菏泽煤电公司 郭屯煤矿，山东 菏泽 274000；2.山东胜宏矿业有限公司，山东 济宁 272500）

0 引言

随着城市建设的高速发展，高层建筑越来越多，基坑工程施工朝着开深、工作面窄、周边房屋及地下管线近的特点发展。当前，基坑变形监测与设计、施工同被列为深基坑工程质量安全保证的三大基本要素。一方面，基坑监测提供动态信息来指导施工全过程，并可通过基坑监测数据来验证基坑设计的科学性，为今后降低工程成本、提高基坑安全性提供设计依据。另一方面，基坑监测可及时预报和发现险情的发生以及险情的发展程度，为及时采取安全补救措施提供有力技术依据。所以说，基坑变形监测已成了工程建设必不可少的重要环节，同时也是指导正确施工，避免安全事故发生的必要措施，对保证人们生命财产安全具有重要意义。

1 卡尔曼滤波模型介绍

基坑监测工程是一个数据长期积累的过程，影响观测量的因素有很多。为了提取主要的影响因素，人们采用各种方法来研究这些变量之间的关联程度，然后根据相关性的强弱，利用最小二乘回归得到一个大体反映该段时间内变量之间相互关系的统计模型。这种模型只能从静态状况做数学上的描述，不能体现监测体的动态特征如速率、加速率等。卡尔曼滤波就是利用相关因子及因子的变率作为状态因子，利用初始时刻附近的观测量，构建动态平差模型，进而解出初始状态值，然后利用状态转移矩阵及观测方程构建卡尔曼滤波模型，它的滤波过程反映的是最新时刻与下一时刻之间状态的转换关系。因此一旦滤波模型构成，它就不再依赖用过的数据。

1.1 卡尔曼滤波模型构建所依赖的基础方程

（1）状态方程

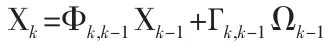
观测方程

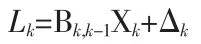
式中Xk、Lk、Δk分别为时刻tk的状态向量、观测向量和观测噪声；Φk,k-1、Ωk-1分别为tk-1至 tk时刻的状态转移矩阵和动态噪声；Гk,k-1、Bk,k-1分别为状态方程和观测方程在tk时刻的系数矩阵。

离散线性系统的卡尔曼随机模型为：

其中，当 k=j时，δkj=1；当 k≠j时，δkj=0。

所谓离散线性系统的卡尔曼滤波，就是利用观测向量L1，L2，…，Lk由相应的状态方程及随机模型求tj时刻状态向量Xj的最佳估值。通常把 Xj的最佳估值记为

（2）状态预报方程

（3）预报误差协方差

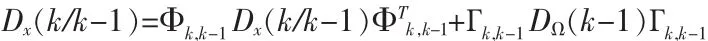
（4）增益矩阵

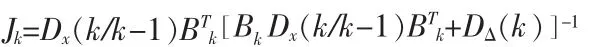
其中，DΔ（k）为观测噪声方差阵，一般假定观测噪声的方差是一定的，取DΔ（k）为动态平差中的观测值的中误差协方差阵。

（5）状态滤波方程

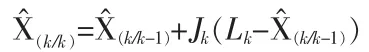
（6）滤波误差协方差阵

1.2 卡尔曼滤波法的实现步骤

（1）首先确定滤波的初值X0，包括：状态向量的初值及其相应的协方差阵Dx（0）、观测噪声的协方差阵和动态噪声的协方差阵DΩ（k）；

（2）建立卡尔曼滤波模型，确定系统状态转移矩阵Φk,k-1、动态噪声矩阵 Гk,k-1和观测矩阵 Bk，k-1；

（4）输入一组观测数据，进行卡尔曼滤波，得出该组观测值的最佳预测值和方差阵 Dx（k/k）；

（5）再回到（3），进行递推计算。

1.3 卡尔曼滤波初值的确定

从卡尔曼滤波递推公式能够发现，要想确定系统在tk时刻的状态，首先需要知道系统的初始状态，即系统的初始值。对于实际问题而言，滤波前系统的初始状态是不能够精确得到的，一般只能近似的给定。

滤波的初值包括：初始状态向量X0及其相应的方差阵Dx（0），动态噪声的方差阵 DΩ（k）和观测噪声的方差阵 DΔ（k）。

对于变形监测的初值问题，可参考文献[4]确定，在此不再详述。

2 实例分析

2.1 基坑工程概况

为了满足XX市环境监控中心的工程施工要求，XX单位于XX年XX月开始对该工程的基坑开挖进行了建筑基坑工程监测，包括沉降观测和位移观测。它的四周布设了10个变形监测点，基坑北部已经挖到-5米，南部已经挖到-3米，基坑西边紧邻科技馆大楼，科技馆大楼层高4层。东边紧邻乡村道路。由于观测数据过多，现将其观测点中的第10期原始观测值列见表1。

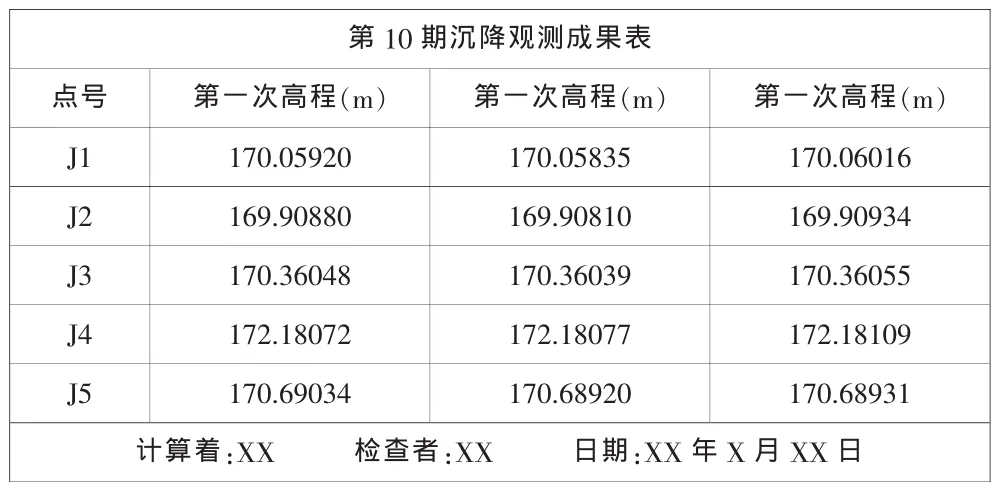
表1 第10期原始观测值（仅列出部分数据）

基准点、工作基点及监测点的分布为图1。

2.2 数据处理

该基坑边坡监测点共有10个，分别为J1，J2，...，J10，每个点观测了20期，观测周期视开挖状况确定。通过采用卡尔曼滤波对完整采集的数据J3监测点进行滤波，运用建立好的模型依次对以后各期数据进行滤波并进行预测，通过对滤波后的数据进行对比，分析观测值与滤波值和预报值的区别。

各监测点观测20期经整理后的数据见表2和表3。

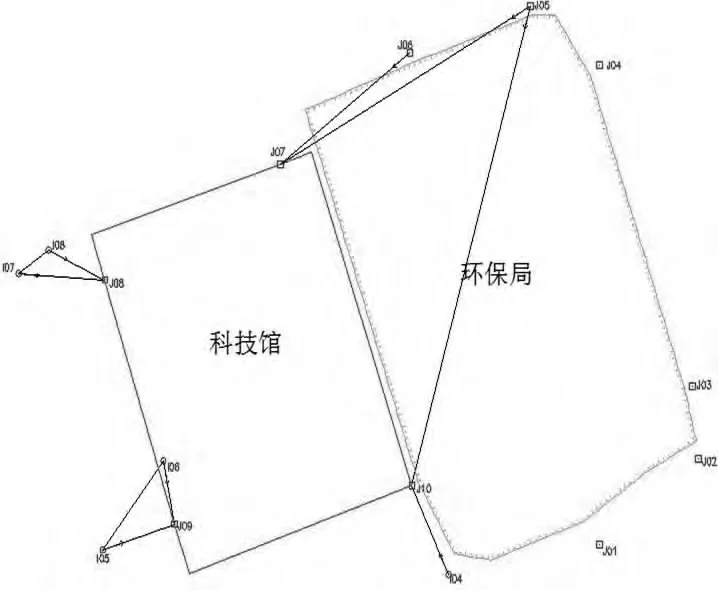
图1 基准点、工作基点及监测点的分布

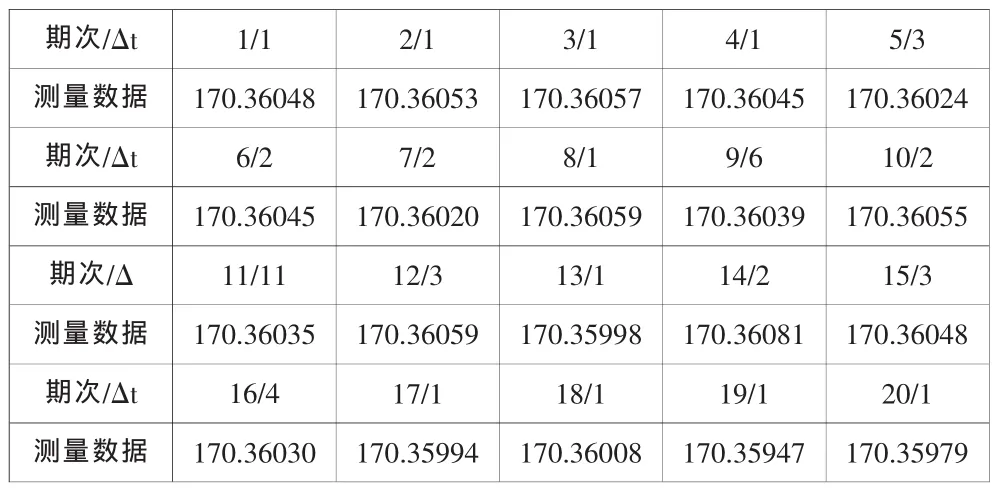
表2 监测点观测20期经整理后的数据（只列出J3点）

对于基坑的变形监测来说，影响变形的因素比较多，比如基坑所在地的工程地质、水文地质和气候条件以及基坑自身的内部结构，喷灌的混凝土应力、及温度、降水等。所以在进行沉降数据处理和分析的时候，为了使结果和实际情况更符合，也应该考虑这些影响因子，把它们当成状态参数的一部分。但是因为上述影响因子的数据难以获取，所以状态参数只考虑水平量和速率。由于这个变形体的动态系统是2维的，观测系统是1维的，所以观测点的状态向量就是。对J3点观测数据进行滤波处理，由前两期的观测数据通过初值确定方法可知X0=[170.36053 0.00005 ]T，Dx动态噪声矩阵观测噪声矩阵 DΔ（k）=0.012，时间间隔 Δt，状态转移矩阵观测矩阵B=[10]。使用的方法为用Excel进行矩阵计算，其结果如下表3。

2.3 精度分析

从表2至表4，图2至图3中可以看出，卡尔曼滤波值、卡尔曼预报值与原始观测值数据曲线的变化逐渐趋向接近，卡尔曼滤波值与原始观测值的最大差值：J3点为0.17mm；单位权方差σ2的估值最大值为0.21，平均为0.13；卡尔曼预报值与原始观测值的最大差值：J3点为0.26mm。相比滤波值其预报值有一定的误差，因为其观测时序较短，影响变形的因子没有一定的变化规律，所以其预报值精度有所降低。

综上说明所建立的卡尔曼滤波模型是合理的、可靠的，较好地模拟了动态目标系统的变化规律。从图表中还可以看到，随着观测点数的增加，观测值与滤波值、预报值的残差越来越趋近于零，也说明模型随着点数的增加不断的进行自身的修正，模型越来越逼近监测系统。

3 总结

本文通过对卡尔曼滤波技术理论的研以及对基坑监测数据进行处理和数据分析，可得出如下几点结论：

（1）卡尔曼滤波是一种对动态系统进行数据处理的有效方法，可以较好地用来处理变形监测数据，也可实时地获得监测系统的当前状态。由于卡尔曼滤波除了可掌握系统的当前状态外，还可以较好的预测系统的未来，因此，对于基坑变形监测来说，卡尔曼滤波是一个重要的研究方法。

（2）在基坑变形监测中，由于滤波方程是一组递推计算公式，计算过程是一个不断预测、修正的过程；在求解时，具有能够求解出速度参数，修正干扰引起的突变；并且当得到新的观测数据时，可随时计算新的滤波值，便于实时处理观测成果，把参数估计和预报有机地结合来。因此，Kalman滤波特别适合基坑变形监测动态数据的处理。

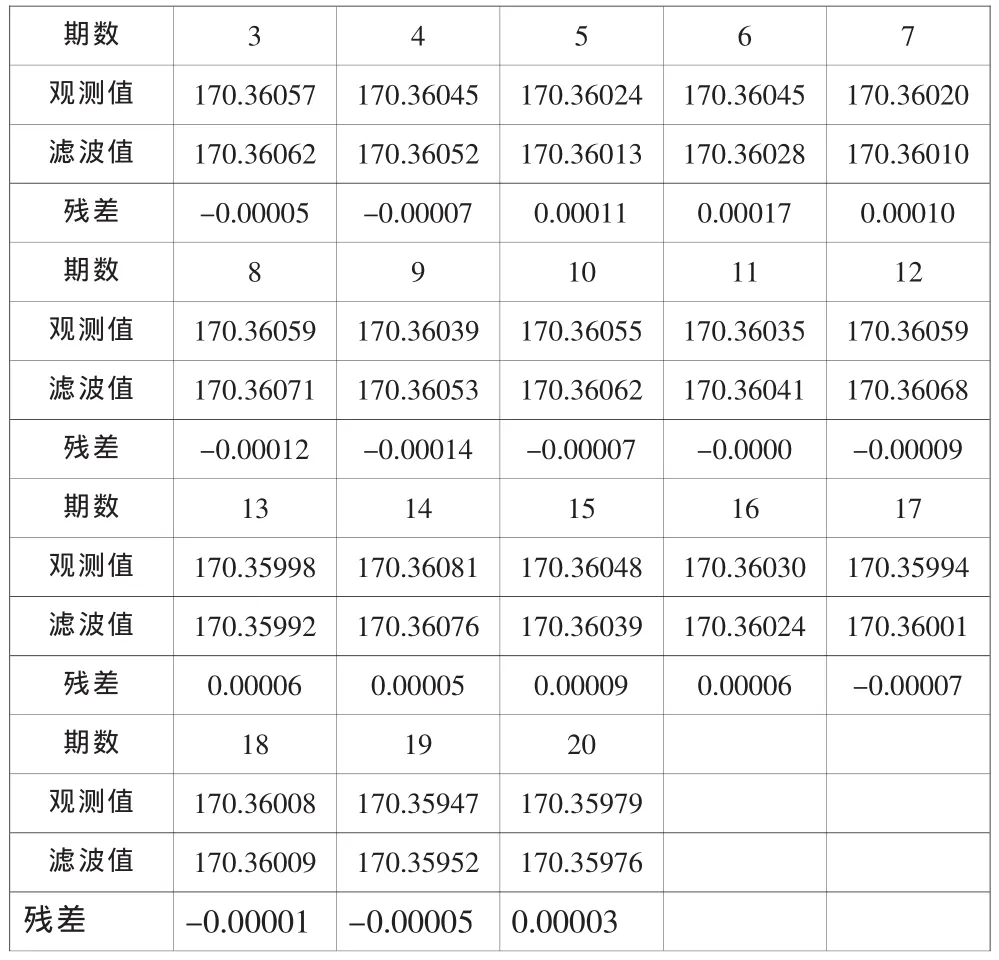
表3 J3点卡尔曼滤波值与观测值对比

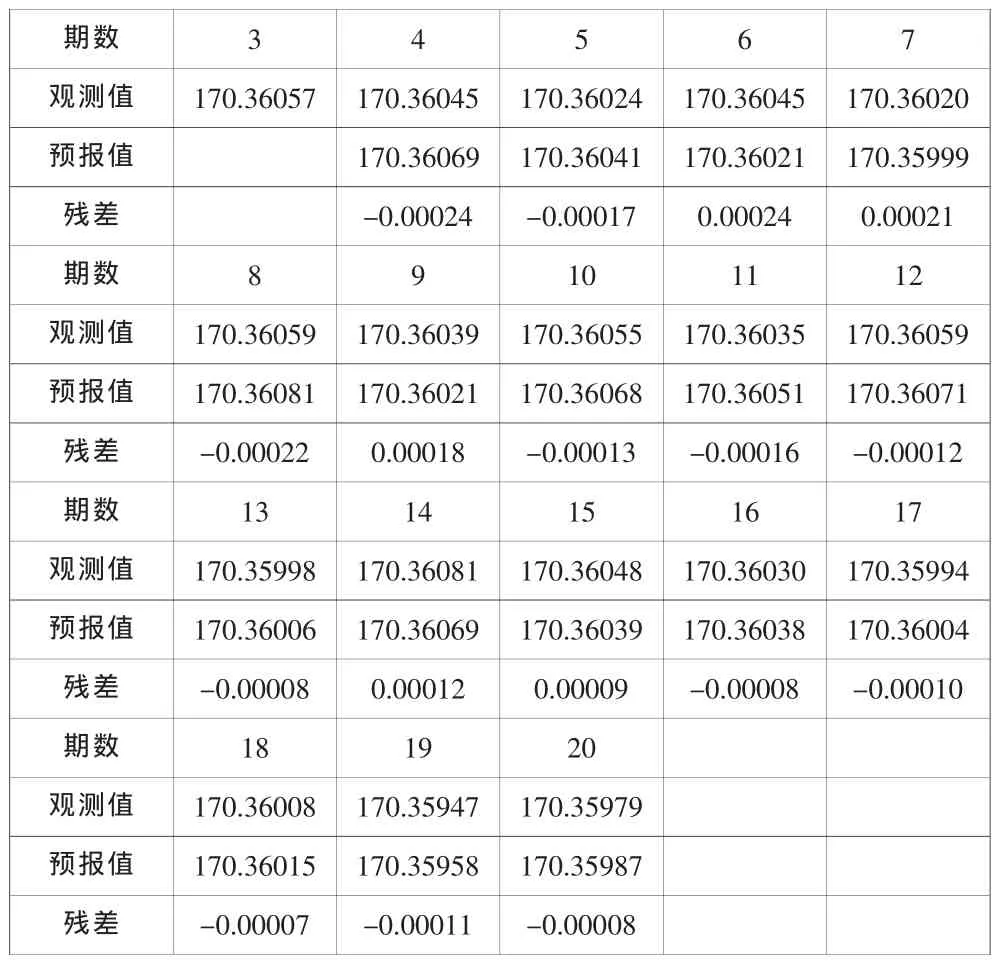
表4 J3点卡尔曼预报值与观测值对比

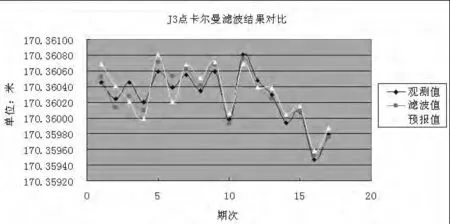
图2 J3点卡尔曼滤波结果对比

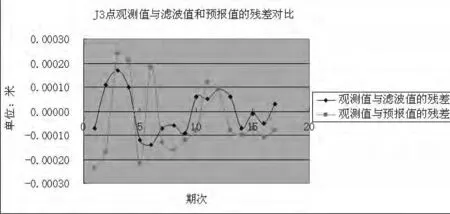
图3 J3点观测值与滤波值和预报值的残差对比

（3）通过文中的分析可以看出，Kalman滤波采用了用残差反求动态噪声的协方差，代入滤波方程改正滤波过程中的原动态噪声协方差，能够较准确的描述变形体的变形状况。

［1］陆如华.卡尔曼滤波方法在天气预报中的应用[J].气象，1994，2:13-216.

［2］于剑飞.某深基坑工程的监测与分析[J].山西建筑，2001,1:22-23.

［3］黄立人.深基坑施工中的变形监测[J].测绘工程,1997,3:7-13.

［4］陆如华,徐传玉,张玲,毛卫星.卡尔曼滤波的初值计算方法及其应用[J],应用气象学报，1997,2:1-8.

［5］王永，等.基于分形的线要素综合数据处理方法[J].矿山测量，2009,10.

［6］李奕,高雅萍,穆建锋.自适应卡尔曼滤波在基坑变形监测中的应用[J].陕西国土测绘工程院,2006,10:23-27.

［7］王永，等.利用 Excel绘制误差椭圆的方法[J].矿山测量，2008,12.