基于容差模型的半挂汽车列车行驶平顺性优化*

陈新志 孙桓五 刘 荣 柳 宁 周 钦

（太原理工大学）

针对平顺性优化，国内、外学者在改善模型精度、算法的应用、控制策略等方面做了大量研究[1～3]。然而传统的确定性优化方法很少考虑到设计变量波动的影响，如悬架刚度或其他位置等参数的不确定性都有可能使目标函数不能保持最优值或约束条件得不到满足，从而使确定性优化失败。针对此问题，本文提出采用基于容差模型的稳健优化方法，降低目标函数对设计变量波动的敏感程度，从概率上保证约束条件得到满足，且在半挂汽车列车行驶平顺性优化设计中进行验证。

1 容差模型稳健性优化原理

产品设计值与制造后和使用中实际值的差异称为设计变量的变差。当这种变差传递给目标函数和约束函数时，会引起质量指标和约束的变差，可能导致目标函数波动明显或约束条件不再满足。而基于容差模型的稳健优化，就是要使得当设计变量x或某些噪声因素z（不可控因素）发生变差时，质量特性对这些变差的影响不敏感，且要求约束条件仍然满足。

图1为容差模型的原理，由设计变量变差Δxi引起约束函数的变差Δgj，为此在设计空间内形成了稳健设计的新可行域再求解，即稳健设计解[4]。修正约束条件为 gj（x¯，z¯）+Δgj≤0 而目标函数的方差最小即可保证质量特性对变差波动的敏感性保持最小。

x

故基于容差模型的稳健优化设计模型可以表示为：

当利用统计容差带建立约束函数时，稳健可行性条件应为：

式中，k为任意常数。

若k=3，考虑x和z的随机变差时，其设计可行率为 99.865%[4]，即：

建立上述模型的关键是计算约束函数的变差和目标函数的方差，而且在优化过程中随着设计变量的变动不断修正约束函数的变差与目标函数的方差。

由于在平顺性优化中众多噪声因素变差难以确定，故忽略其影响，则设计函数（约束函数和目标函数）与设计变量之间是非线性关系：

将上述设计函数在均值处展开泰勒级数且忽略2阶以上的高次项：

然后对其求均值和方差：

当任意两个设计变量之间相互独立时，即相关系数ρij=0，上述设计函数的均值和方差可以简化为：

利用式(5)和式（6）或式（7）和式（8）可求得目标函数的期望及方差，利用式（4）或（6）可求得约束函数的方差，进而求得其变差。

2 整车9自由度平顺性模型及评价指标

2.1 整车9自由度平顺性模型

本文考虑对汽车平顺性影响较大的垂直振动和纵向角振动，忽略横向水平振动，且在做出如下假设条件[5]的基础上，建立了牵引车—半挂车振动力学模型：

a. 车辆各部位视为刚体振动，且车身在平衡位置作微幅振动；

b.刚度和阻尼分别和相应的位移和速度成线性关系，轮胎阻尼忽略不计；

c. 汽车等速直线行驶。

此外，牵引车和挂车之间通过鞍座连接，一般情况下挂车可以绕牵引销轴线回转。当整车仅考虑垂直振动时，由于牵引车和挂车之间鞍座约束导致挂车垂直自由度和绕横轴的俯仰运动只有1个有效自由度。

建立的9自由度线性振动力学模型如图3所示。其中，Z1是牵引车人椅系统的垂直位移；Z5是牵引车车身簧载质量绕质心轴的俯仰角；Z4、Z9是牵引车车身、半挂车簧载质量质心垂直位移；Z2、Z3、Z6、Z7、Z8 是牵引车前轴、后轴、半挂车车轴非簧载质量垂直位移。

根据上述简化的力学模型，由广义拉格朗日方程推导出振动微分方程为：

对于某款半挂汽车列车，有关参数如下：

2.2 路面模型

根据GB/T7031－2005《机械振动道路路面谱测量数据报告》[6]给出空间频率路面谱密度的拟合表达式：

将 Gq（n）换算为时间频率路面谱密度 Gq（f）：

式中，Gq（n0）为路面不平度系数；n为空间频率；n0为参考空间频率，n0=0.1m－1；ω 为频率指数，取 ω=2；v为车速；f为时间频率。

假设汽车沿同一直线轨迹行驶，则对于5轴半挂汽车列车平面模型，第2、3、4、5车轮的不平度路面函数相对第1车轮滞后距离为Li，因此各轴车辆路面不平度输入可以表示为：q1（I）=x（I）；q2（I）＝x（I－L1）；q3（I）＝x（I－L2）；q4（I）＝x（I－L3）；q5（I）=x（I－L4）。其中，L1=L1+L2；L2=L1+L5+L6－L4；L3=L2+L7；L4=L3+L8

对于平面5轴模型，要考虑5个车轮输入的自谱和各车轮之间的互谱共 25 个谱量，Gik（n）（i，k=1，2，3，4，5），其中 20 个互谱量两两共轭，Gik（n）按下式计算[7]：

式中，Fi（n）、Fk（n）为 qi（n）和 qk（n）的傅里叶变换；（n）、（n）为 Fi（n）、Fk（n）的共轭复数；T 为长度 I的分析区间。

5个车轮的路面不平度函数傅里叶变换为：F1（n）=F[q1（I）]=F[x（I）]X（n）

将5个车轮的路面不平度函数傅里叶变换代入式（12），同时考虑到每个车轮自谱为 Gq（f），则有：

可以得到平面模型的5轮输入功率谱密度矩阵：

2.3 平顺性评价指标

根据GB/T 4970－2009《汽车平顺性试验方法》[8]推荐的基本评价方法，通过计算牵引车驾驶员座椅处的加速度均方根值来评价牵引车平顺性能，即：

其中，w（f）为加权函数：

在线性系统中，依据随机振动理论，有：

式中，GZ1¨（f）为加速度功率谱密度；G（f）为路面输入谱密度；H*（f）为系统频率响应函数的共轭；HT（f）为系统频率响应函数的转置。

对振动微分方程（9）进行傅里叶变换，即可求得系统频率响应函数H（f）：

由于难以直接对设计函数式（13）求偏导数，并且也难以对悬架动挠度和轮胎动载荷表达式求偏导数，因此需要近似函数来代替，一般情况下可以通过二次回归正交组合试验设计得到式（13）的近似回归方程如下：

本文考虑通过优化设计得出和某款牵引车匹配最佳的半挂车参数, 获得最佳乘坐舒适性，因此选取影响整车平顺性能的半挂车参数：鞍座位置参数L4，半挂车悬架刚度值 K6、K7、K8，并对各个设计函数进行二次回归正交组合试验设计，以获得回归显著地回归方程。

3 整车平顺性优化设计

3.1 确定性优化模型

为了获取最佳的半挂车参数，以驾驶员座椅处的垂直加速度均方根值az1为优化目标函数，L4、K6、K7、K8为设计变量，为了保证汽车整车行驶，悬架动挠度fdi和轮胎动载荷Fdi需要保持在适当范围内，即需要满足以下条件：

式中，fdi为第i轴悬架动挠度；[fdi]为第i轴悬架限位行程；Fdi为第i轴轮胎动载荷；Gi为第i轴轮胎承受的静载荷。

当式（17）成立时，悬架撞击限位的概率为0.3%[7]，保证了悬架不会频繁的撞击限位块；当式（18）成立时，车轮跳离地面的概率为0.15%[7]，减小了轮胎和地面的动载荷。 用 gi≤0，i=1，2，3···，10 代替式（17）和式（18）作为优化的约束条件，其中，式（17）中 i=1，2，3，4，5，式（18）中 i=6，7，8，9，10。

半挂车质心位于支撑装置与后轴之间稍前方的位置，一般牵引座都安装在牵引车后轴前方大约0.3～0.6 m的地方，一般公路用车后悬架静挠度取50～65 mm[10]，故有：

式中，Mi为簧载质量。

经计算确定 K6、K7、K8被限制在 829 442～1 078 274N/m之间，因此构建确定性优化模型：

3.2 基于容差模型的稳健性优化

取设计变量容差为名义值的1%，即：

建立基于容差模型的稳健性优化模型如下：

其中，Δgi=3σgi；Var（az1）和 σgi按照式（8）计算；E（az1）由式（7）计算；ε 取 0.05。

3.3 优化结果及分析

确定性优化和稳健性优化结果如表1和表2所示。经过确定性优化后，加速度均方根值从1.9623降到1.376 8，降低29.84%。经过稳健性优化后，加速度均方根值从1.962 3降到1.425 4，降低27.35%。由此说明两种优化方式都能有效改善整车平顺性能，达到优化目的。从表1最后一行中加速度均方根值的均方差可以看出，稳健性优化的均方差较确定性优化减小了8.6%，证明稳健性优化更加稳定可靠。从表2可以看出，由于约束条件的限制，动挠度和动载荷保持在合理范围内，故优化结果可以接受。

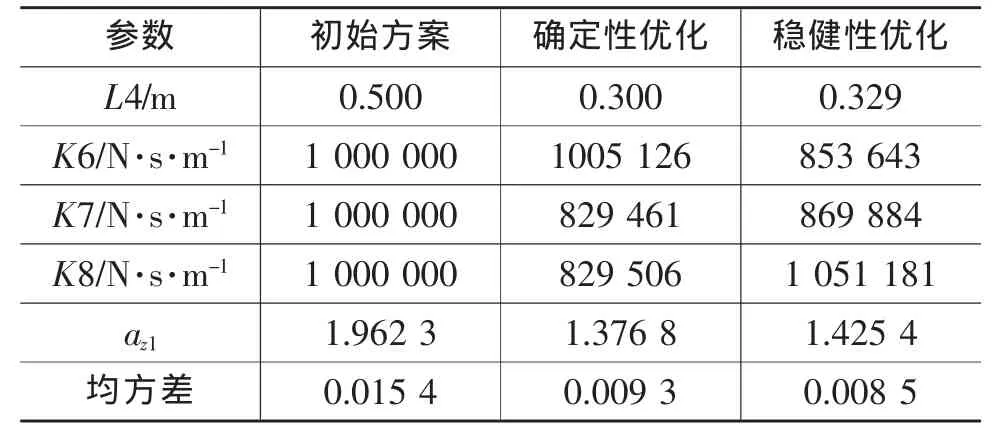
表1 优化结果

表2 优化前、后约束条件变化

通过使用蒙特卡洛随机模拟方法，抽取10000个随机样本，计算在设计变量发生波动时约束条件满足的概率，计算结果如表3所列。

表3 确定性优化和稳健性优化约束条件满足的概率对比 %

从表3可知，采用确定性优化时，若设计变量发生波动，约束条件g8即整车第3轴轮胎动载荷约束条件满足的概率仅为90.84%,不能保证足够的可靠度。这主要是因为确定性优化在迭代过程单纯为获得目标函数的最优解而未考虑到设计变量发生波动时可行域会发生变化。但是同样情况下，稳健性优化结果对约束条件保持了100%的满足概率，这是由于在迭代过程中动态调整了可行域范围，使得约束条件能够以一定概率被满足。

综合加速度均方根值和约束条件两方面可知，采用稳健性优化方法与采用确定性优化方法相比不仅能够提高整车平顺性能，而且能够保证优化可靠性，更加符合工程实际情况。

4 结束语

a.建立了9自由度半挂车汽车列车平顺性模型，通过建立基于容差模型的稳健优化模型，对汽车平顺性进行了稳健性优化。

b. 通过稳健性优化和确定性优化的分析结果对比表明，稳健性优化不仅能够实现优化目的，而且较确定性优化更能降低目标函数对设计变量波动的敏感程度，当设计变量在最优解附近发生波动时，也能保证整车平顺性达到最优，提高了优化结果的稳健性。

c.在约束条件稳健性方面，稳健性优化几乎能够在设计变量发生波动时以100%的概率保证约束条件满足。

1 熊飞.以刚弹耦合模型为基的运动车平顺性仿真分析.现代制造工程，2010（05）:53～57.

2 段敏,张立军,石晶，等.基于神经网络的轻型客车悬架参数的优化.汽车工程，2003（02）:190～197.

3 郭孔辉,王金珠,郭耀华，等.基于混合阻尼控制的车辆半主动悬架可调性研究.汽车技术,2013（03）:1～5.

4 陈立周.稳健设计.北京：机械工业出版社，2000.

5 张义，莫旭辉，钟志华．基于MATLAB的菱形客车平顺性研究.中国机械工程，2012，20（7）：875～880.

6 GB/T7031－2005.《机械振动道路路面谱测量数据报告》.

7 余志生.汽车理论第五版.北京：机械工业出版社，2009：210～218.

8 GB/T 4970－2009.《汽车平顺性试验方法》.

9 潘丽军，陈锦权.试验设计与数据处理.南京：东南大学出版社，2008.

10 郭正康．现代汽车列车设计与使用.北京：北京理工大学出版社，2006：213～321.