利用遥感SST反演上层海洋三维温度场*

张春玲 许建平, 3 鲍献文 王振峰 刘增宏 孙朝辉



利用遥感SST反演上层海洋三维温度场*

张春玲1, 2许建平1, 2, 3鲍献文1王振峰4刘增宏2, 3孙朝辉2

(1. 中国海洋大学海洋环境学院 青岛 266003; 2. 国家海洋局第二海洋研究所 杭州 310012; 3. 卫星海洋环境动力学国家重点实验室 杭州 310012; 4. 东海舰队司令部海洋水文气象中心 宁波 312122)

通过统计相关分析验证了一个简单的温度参数模型在太平洋海域的较好适用性。基于Argo观测资料及WOA09气候态温度数据, 采用最大角度法求得此模型的相关参数, 并利用高分辨率卫星遥感海表温度反演了太平洋上层海域空间分辨率为1°×1° 的气候态月平均三维温度场。与实测资料的比较分析表明反演结果是较为真实可靠的, 并可作为海洋数值模式积分的初猜场, 为实现现场观测(如: Argo)与卫星观测的优势互补, 构建太平洋海域完整的三维温度分析场提供一种新途径。

温度参数模型; 最大角度法; Argo观测; 海表温度(SST); 反演

目前, 来自于Argo、CTD、XBT、海洋站的温盐观测剖面日益增多。特别是海量增加的Argo浮标观测剖面, 已成为全球海洋观测系统的重要支柱, 但其目前仍缺乏表层观测且空间观测分辨率较低。而另一方面, 随着卫星遥感技术的不断发展, 特别是与此有关的卫星遥感海面温度(Sea Surface Temperature, SST)和卫星观测海面高度(Sea Surface Height, SSH)资料的日益增加, 为海面监测提供了大量覆盖范围广、精度和空间分辨率较高、时间连续性较强的海洋表面实时和准实时的信息。然而, 卫星观测不能给出任何直接观测的次表层信息。因此, 如何借助已有的资料统计分析方法, 将现场观测(Argo、XBT、TAO、TRITON、PIRATA等)与卫星观测相结合, 充分发挥各自的优势, 构建完备的三维温、盐度场, 业已成为国际海洋研究领域中急需解决的问题。

早在20世纪80年代末, 将海面信息(海面温度或海面高度)映射到海洋内部, 从而反演温、盐度剖面的不同方法就已被提出。如动力学方法(Hurlburt, 1986)和统计法(Khedouri, 1983; Witt, 1987; Carnes, 1990; Gavart, 1997)。这两种方法均包括联合应用卫星测高和遥感海面温度数据。许多研究证明, 利用这两类遥感数据反演获得的深海或大洋温盐剖面信息作为相应数值预报的初始场, 较单独利用遥感海面温度反演的温度剖面好很多(Hurlbtrt, 1990; Carnes, 1994; Pascual, 2003; Gavart, 1999; Fox, 2002; Bruno, 2004; Guinehut, 2004; 王喜东等, 2011)。而在研制三维温盐流数值预报系统时, 启动海洋模式积分需要提供网格化、接近实际的气候态累年各月平均的初猜场。但目前由观测统计形成的多年月平均数据, 包括WOA09的月平均数据, 许多网格无统计值。Thacker和Long(Thacker, 1988)给出了对海洋和大气模式都适用的结合动力模式与观测资料的变分法公式; Yan等(2004)基于三维变分数据同化方法, 利用海表动力高度来估计温、盐度剖面, 并考虑了垂向相关及非线性温盐关系。这种方法基于变分原理, 且计算量较大。

Chu等(1997a, b)提出一个包含五个深度和对应的梯度及海表温度等十个参数的温度参数结构模型, 并采用迭代法计算模型参数, 从而由海表温度观测确定次表层温度结构。为减少自由度, Chu和Fan (2000)给出了南海海域的简化模型(六个参数), 本文通过相关分析检验验证了其在太平洋上层海域的适用性。采用最大角度法(Chu, 2011), 基于2011年8月份的Argo观测资料计算混合层深度, 并利用同期的WOA09气候态数据计算温跃层梯度及温跃层下边界深度。进而借助于同期的卫星遥感SST资料反演了2011年8月份太平洋海域, 空间分辨率为1°×1°的三维温度场。通过与实测资料作对比, 评估了反演结果的可靠性, 为缩短模式积分年限, 构造完整的三维温度分析场, 实现现场观测与卫星观测优势互补提供新途径。

1 资料来源及处理

1.1 卫星遥感SST

卫星遥感观测作为海洋观测数据的一个重要来源, 可以为海面监测提供大量覆盖范围广、精度和空间分辨率较高、时间连续性较强的海洋表面实时和准实时的信息, 解决了传统海洋表层温度观测资料的非同步缺陷。但是, 由于海温传感器提供的仅是海洋表层信息, 无法直接获得海洋三维温度结构特征。这里, 作者采用由美国国家海洋和大气管理局(ftp://eclipse.ncdc.noaa.gov/pub/OI-daily-v2/NetCDF/2011/AVHRR/)提供的太平洋海域2011年8月份的卫星遥感SST数据近似的作为海洋混合层温度, 并将该月31天的SST数据加以平均得到此月的月平均SST数据。

1.2 Argo观测资料

Argo剖面浮标可以在海上进行长期的定时、循环观测, 从而快速、准确、全面地收集全球海洋中、上层水体的温度、盐度垂向剖面资料。大多数Argo浮标的观测周期为10天, 目前新型Argo浮标的观测周期甚至达到2天, 但常规的一般只能观测5—2000m深度的上层海洋温、盐度值, 因此, 作者采用Argo浮标观测资料来计算参数模型的短时间尺度变化参数。本文采用的Argo原始散点数据由中国Argo是实时资料中心(http://www.argo.org.cn/)提供, 这里选用太平洋海域(60°S—60oN, 120°E—80°W)的2011年8月份温、盐度观测资料, 经过观测参数及观测层数检验、水陆点及区域检测、温度范围及时间判断等简单的质量再控制后, 共包括5056个剖面, 并将其通过Akima插值(Akima, 1970)垂向插值到25个标准层(10—2000m)。

1.3 WOA09历史数据

WOA09数据是通过对长时间序列的多种观测进行客观分析得到的全球海洋三维温、盐度格点数据, 其能够反映海洋温、盐度年际变化特征, 故作者利用其计算参数模型的长时间尺度变化参数。这里选用的太平洋海域2011年8月份月平均三维温度场由全球海洋数据中心(National Oceanographic Data Center, NODC)(http://www.nodc.noaa.gov/OC5/WOA09/woa09data.html)提供。

2 反演方法

2.1 温度参数模型

Chu和Fan(2000)给出了与海表温度相关联的次表层温度参数的简化模型(图1)。一个温度剖面可以由式(1)来简单描述:

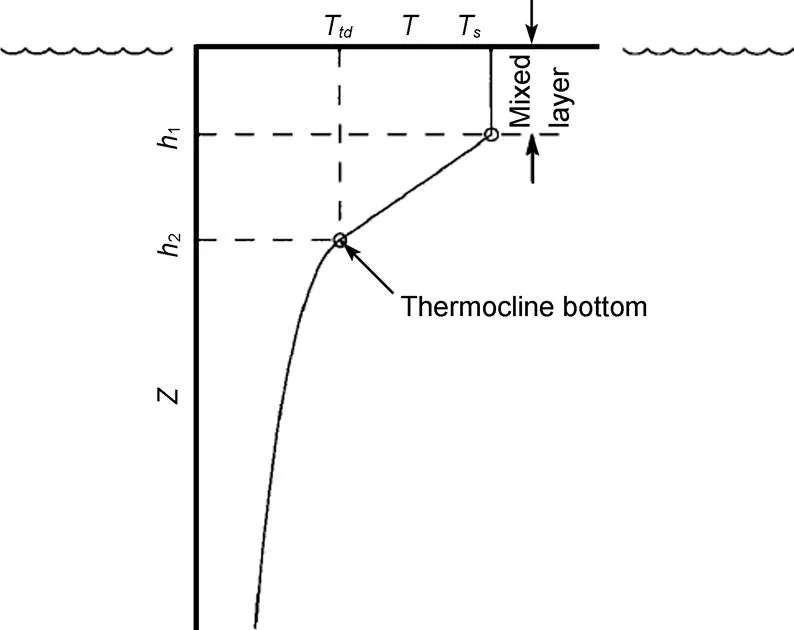
图1 温度参数模型

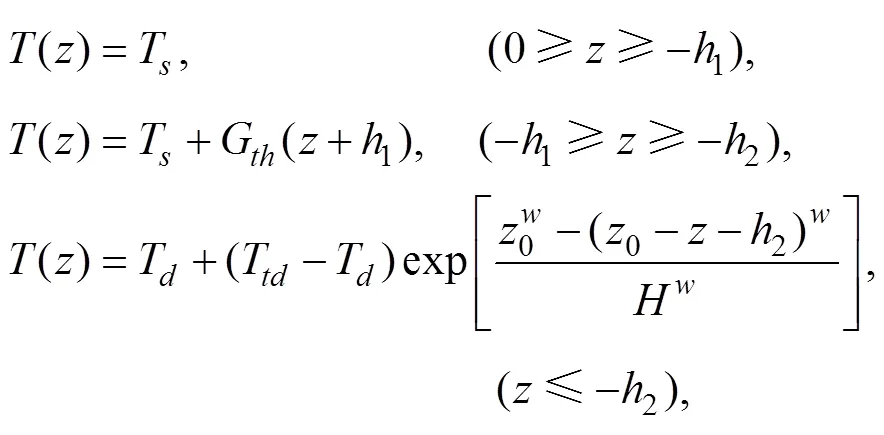
式中,T是海表温度;1,2分别为混合层深度 (Mixed Layer Depth, MLD)(或温跃层上界深度)和温跃层下界深度(Thermocline Bottom Depth, TBD);G为温跃层梯度(Thermocline Temperature Gradient, TTG);T是对应于温跃层下界深度(2)处的温度;T为水深温度, 本文取为WOA09多年平均数据中2000m深处对应的温度;为次表层e-折尺度, 在太平洋海域取= 2000。另外,0和是为了保证()和′()在TBD处的连续性追加的两个参数, 即:

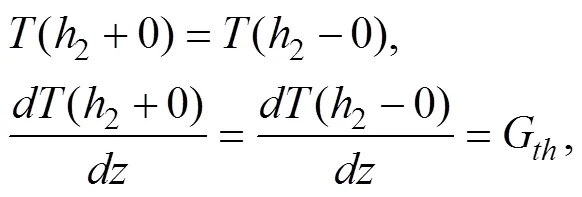
由式(1)对求导, 并结合式(2), 可得:

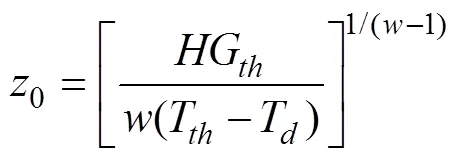
参数不能大于或等于1, 否则将使得0的值很大, 从而导致温度随深度的增加而递增。的值也不能等于0, 此处取= 00.5。因此, 一个垂向温度剖面可以提取七个参数(T,T,T,1,2,,G), 并且由()在TBD处的连续性可得:

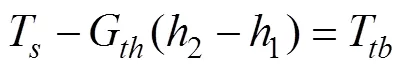
故, 七个参数中任意六个都可以决定一个温度剖面, 自由度为六。应用此模型, 通过海表温度观测来反演海洋次表层温度场, 关键是确定1,2,G, 本文采用最大角度法来确定这三个参数。

2.2 最大角度法

Chu等(2011)提出了一种简单的客观方法(最大角度法)来确定混合层深度。这种方法具有较强的理论基础, 其不仅用到了混合层的主要特征——温度(或密度)垂向一致, 而且用到了混合层以下跃层的主要特征——梯度巨变。为了更准确的使用此方法(要求观测变量随深度变化具有严格的单调性), 作者用密度混合层深度代替温度混合层深度, 即不考虑障碍层的存在。

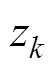
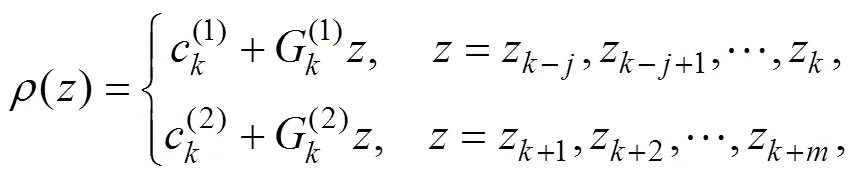
如图所示, 在等密度层, 角达到最大值(图3b)。因此, 最大角度原理可以用来确定混合层深度(max,H→z)。在实际应用中,较难计算其度数, 作者用正切值来代替, 即:

其中,(1)≈0为混合层的垂向梯度,(2)为跃层梯度。由给定的拟合系数可得,

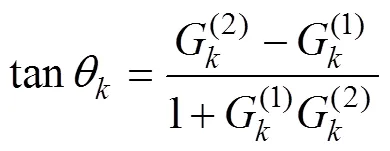
当观测剖面为温度剖面时, 只需将拟合矢量Vector-1, Vector-2改变方向, 其原理与密度剖面相同。为了尽可能保证观测剖面的单调性, 本文利用Argo观测剖面计算混合层深度时, 采用密度剖面的最大角度法, 利用WOA09数据计算温跃层梯度及温跃层下界深度时, 则采用温度剖面的最大角度法。

3 相关分析(correlation analysis)检验

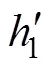
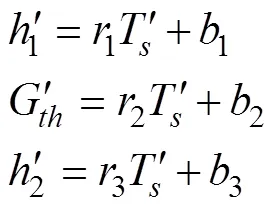
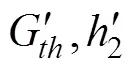
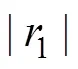
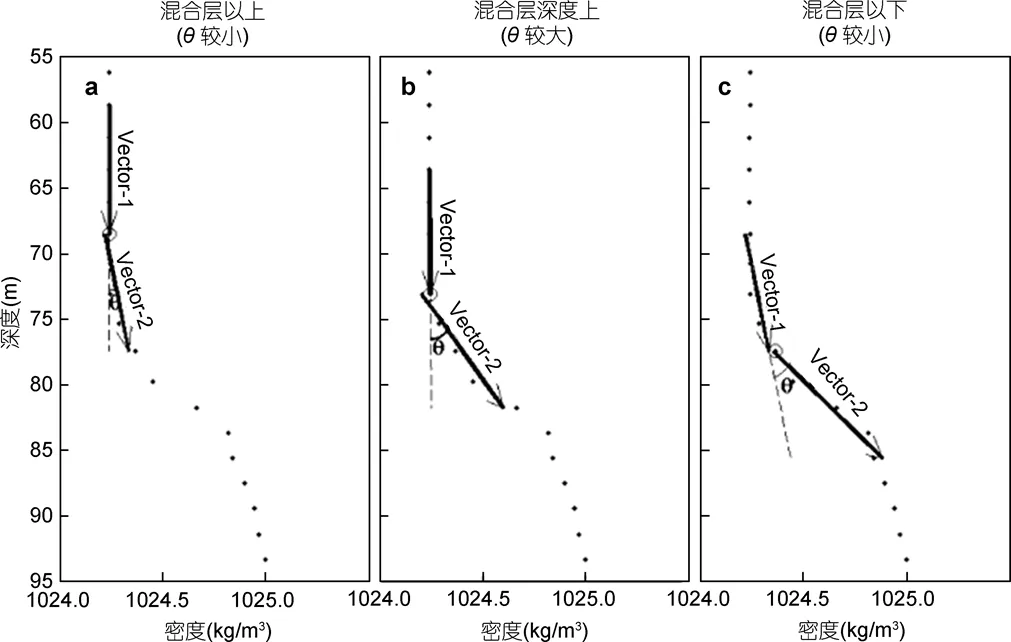
图3 最大角度法原理

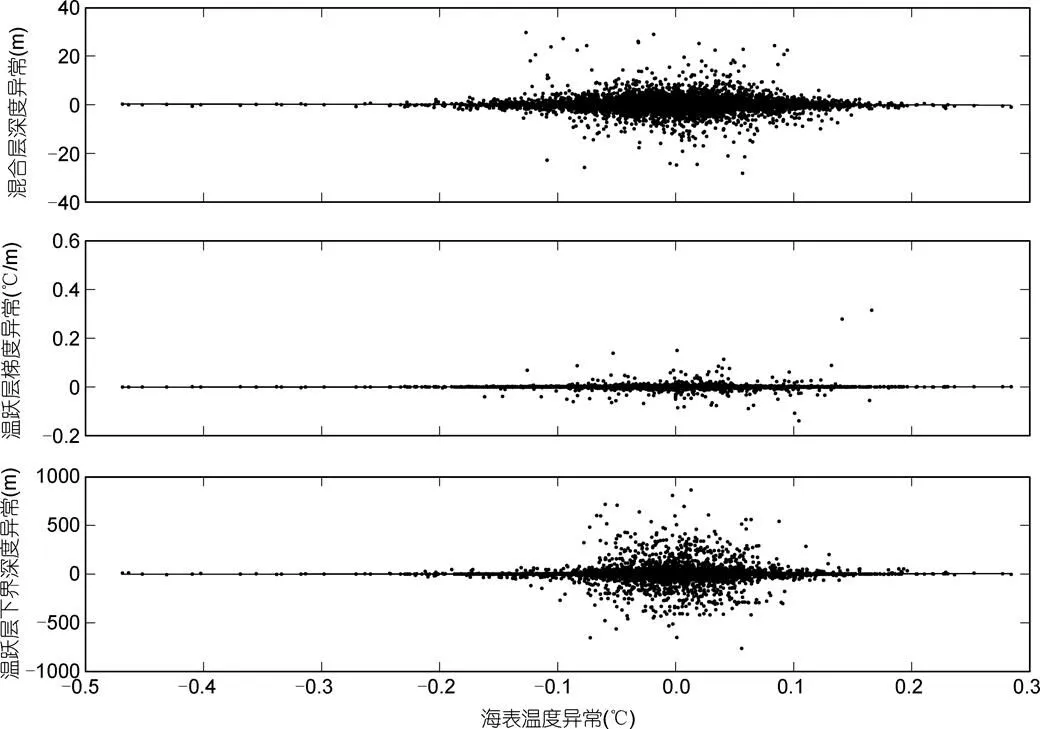
图4 不同参数异常随海表温度异常变化的散点分布: (a), (b), (c)

表1 各参数与SST异常的相关系数及其对应的值

Tab.1 The correlation coefficients between parameters and SST anomaly and the corresponding t values

4 反演步骤及结果

本文利用海表温度观测反演太平洋上层温度场主要分三个步骤: 首先, 借助于Argo观测资料, 采用密度剖面的最大角度法计算混合层深度(1), 并通过最优插值(Behrinoer, 1998)将各参数插值到 1°×1° 的网格上; 然后利用WOA09气候态温度数据, 通过温度剖面的最大角度法确定太平洋海域 1°×1° 网格点上的长时间变化尺度参数(2,); 最后, 利用同期的NOAA海表温度观测, 通过2.1节的(1)式反演太平洋海域的上层海洋气候态三维温度场。

4.1 参数计算

首先由Argo观测剖面的温、盐度数据计算各个剖面在其每个观测层上的密度值, 从而将每个剖面记为[(z),(z)], 通过2.2节的最大角度法((5)—(7)式)得出每个剖面对应的密度混合层深度H, 并忽略障碍层的存在, 用密度混合层深度代替温度混合层深度, 即,1≈H。

作者通过最优插值将MLD插值到1°×1°的网格上, 其水平分布及纬向平均如图6所示。在MLD的水平分布图中, 南太平洋40°S以南的区域存在等深线的密集区, 反映了温跃层在这里迅速消失, 温跃层在此区域具有断面结构。结合其纬向平均曲线不难看出, 太平洋20°N以北大部分海域的MLD是10—20m, 20°N以南的海域MLD普遍较大, 尤其在南太平洋, 大部份海域的MLD超过70m。2011年8月份太平洋海域的MLD由北向南大体呈逐渐递增的趋势(图6右)。

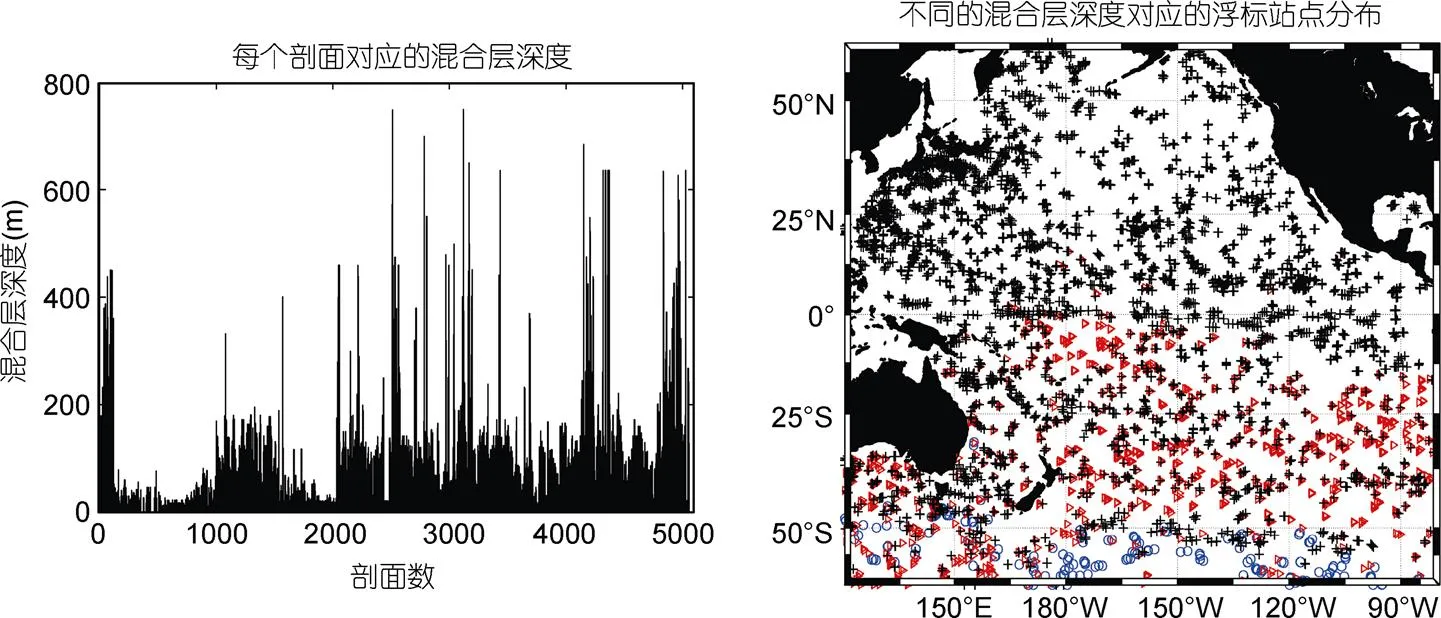
图5 Argo观测剖面的MLD及对应的浮标站点分布

＋: 0—100 m (3797个);△: 100—300m (1075个); ○: 大于300m (184个)

图5与图6展示的混合层深度分布规律与前人(周燕瑕等, 2002; 王彦磊等, 2008; 芦静等, 2008)的研究结果基本吻合。

图7给出了G与2的水平分布及其对应的纬向平均分布。温跃层梯度基本在0—0.2°C/m之间; 10°S—10°N之间的海域, TTG的值均已超过0.05°C/m; 而相比南太平洋, 北太平洋大部分海域有较强的TTG, 特别是赤道太平洋到北纬20°的海域, TTG基本在0.05°C/m以上。由TTG的纬向平均图也可以看出, 北太平洋平均TTG都高于0.06°C/m, 10°N附近海域达到0.1°C/m以上; 南太平洋大部分海域平均TTG都低于0.05°C/m, 特别是40°S以南, TTG几乎接近零, 这也反映了在此海域不存在明显的温度跃层。混合层下界基本在100m以深, 结合其纬向平均分布图, 很显然, 由于8月份北半球洋区跃层比较明显, 因此对应的TBD也比较浅, 平均小于300m; 而南半球的TBD相对普遍较深, 平均为300—500m, 在25°S左右甚至达到1000m以上; 而赤道太平洋的TBD基本为300m左右。但在40°S以南的洋区存在明显的低值等深线密集区, 这是由于在此区域温跃层基本消失, 利用温度剖面的最大角度法时, (7)式的最小值对应的深度值2→z有可能接近混合层深度。因此, 在以下利用海表温度反演次表层温度场时, 作者在2<1时, 只选用(1)式的前两个公式进行计算。在20°N附近存在一个高值区, 平均达到近400m, 而在50°S以南, TBD迅速减小至100m以下, 但总体上, TBD的纬向平均由北向南大致呈逐渐递增的趋势。

4.2 利用遥感SST反演上层海洋气候态温度场

作者由2.1节的(1)式及由4.1节确定的参数1,2和G, 通过SST数据来反演太平洋上层海域温度场。图8给出了170°W经线与5°N纬线的温度断面分布。通过与W0A09 8月份多年平均的温度剖面分布作对比, 可以得出, 虽然反演结果的两个断面较WOA09气候态数据都有明显小尺度波动, 但其温度经向(纬向)变化趋势及温度值的分布均与气候态数据基本吻合, 较真实地反映了2011年8月份经向(纬向)的温度变化情况。由170°W经线断面图可以看出, 南北纬40度附近的等值线分布规律与气候态数据差别较大。5°N纬线断面显示, 西太平洋的反演结果比东太平洋相对精确。

由150m层的温度场水平分布(图9)也可以看出, 受海表温度观测的影响, 本文反演的温度场存在较多小尺度波动, 但仍能够较好地刻画温度的水平分布特征。等温线的分布, 沿纬线大致呈带状分布, 特别在南半球40°S以南海域, 等温线几乎与纬圈平行。在副热带到温带海区, 特别是北半球, 等温线偏离带状分布, 西部向极地弯曲, 东部则向赤道方向弯曲, 这种格局造成太平洋西部水温高于东部。由热赤道向两极, 水温逐渐降低, 最高温度出现在赤道附近海域, 在西太平洋近赤道海域, 可达26—28°C。

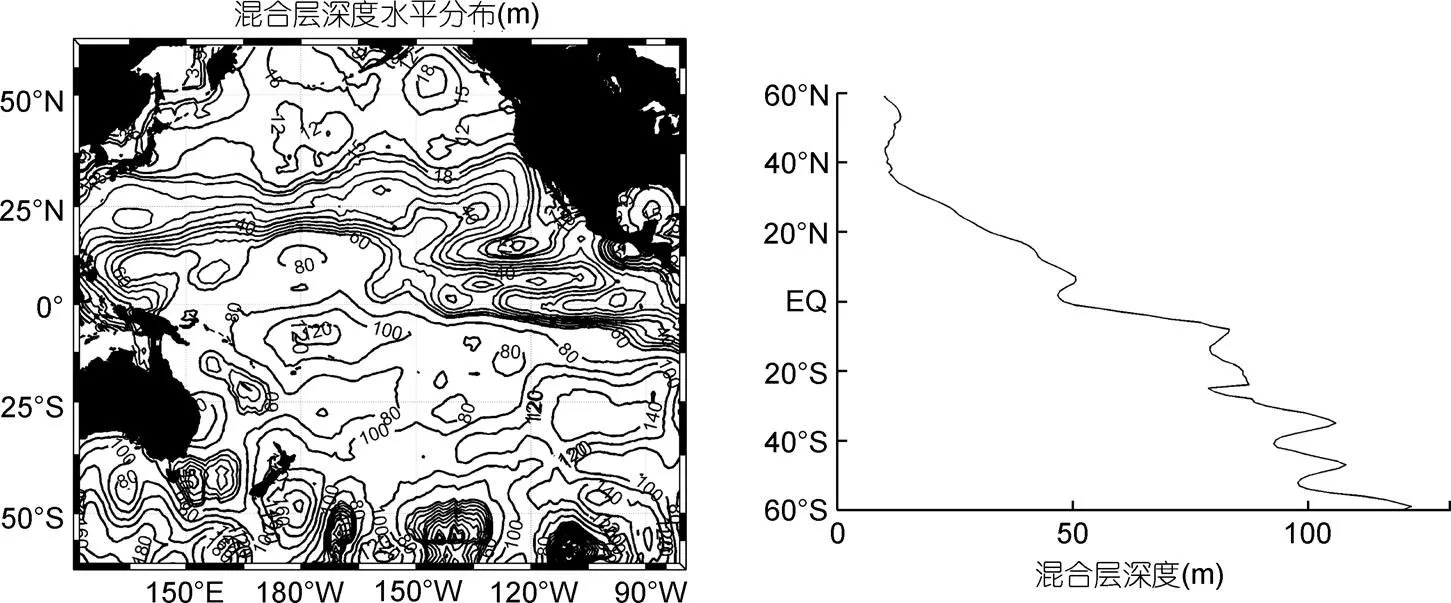
图6 2011年8月份太平洋海域MLD分布(左)及其纬向平均曲线(右)

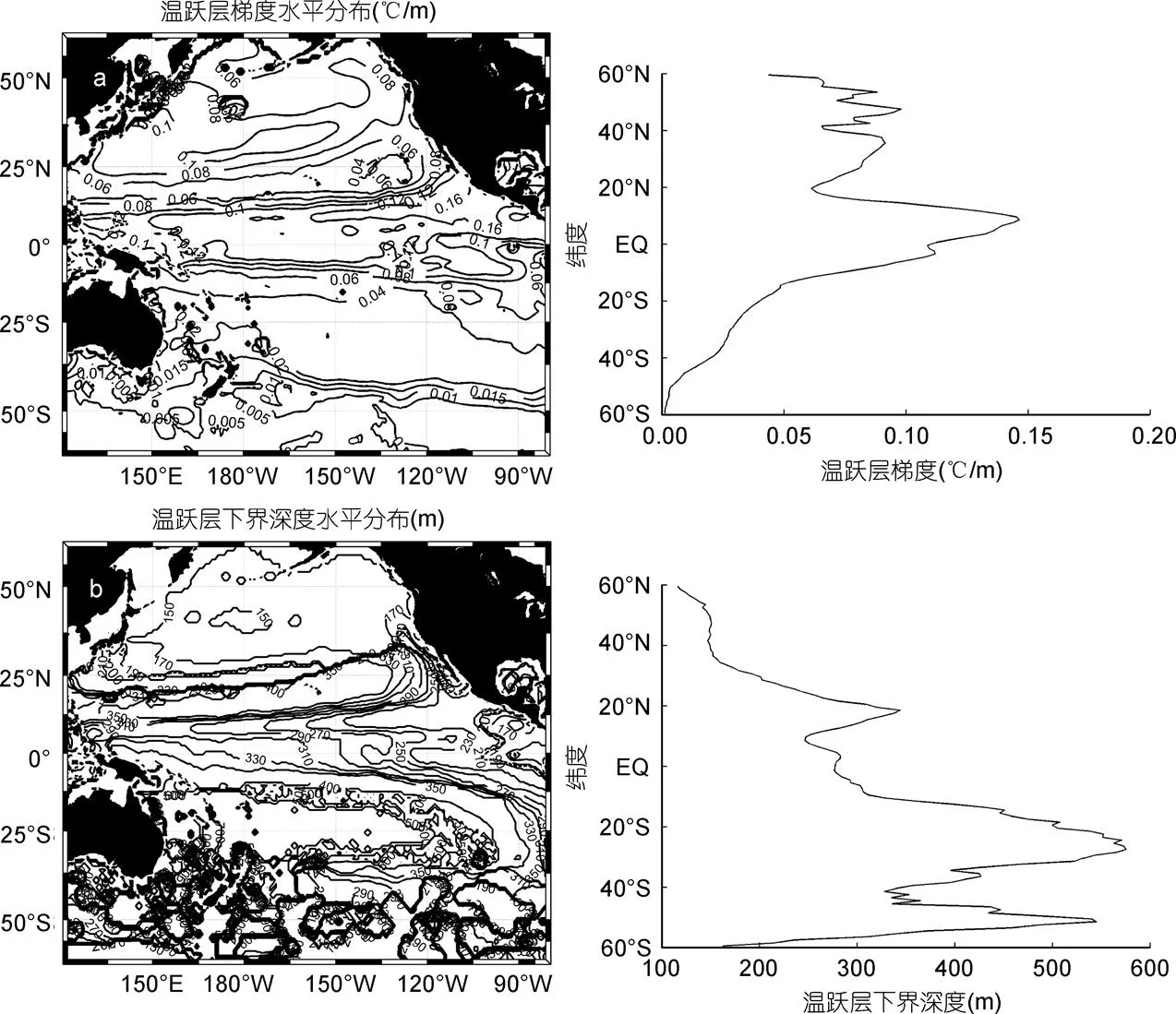
图7 2011年8月份太平洋海域的TTG与TBD分布及对应的纬向平均曲线: a: TTG; b: TBD

由于海表温度只对上层海洋水温有较明显的影响, 因此, 本文利用海表温度观测反演的次表层气候态温度场与Argo观测数据的均方根误差随深度的增加大致呈逐渐增加的趋势, 但2000m以浅的RMSE 均在1.3°C以内(图10)。100m以浅RMSE均小于1°C; 结合图6、图7可以看出, 在100—200m, 2011年8月份太平洋海域的温跃层比较明显, 其对应的RMSE相对较大, 基本超过了1°C; 在200m以深又大体呈递增趋势, 500m处的均方根误差达到了1.19°C。由于下层水温垂向变化相对较小, 500m以深, 特别是1000m以下, 均方根误差又逐渐减小。

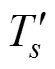
作者分别在南太平洋(10°S —50°S)、赤道太平洋(10°S—10°N)、北太平洋(10°N —50°N)各随机选取4个均方根误差比较大(大于1°C)的观测站点, 将观测剖面与反演结果进行垂向对比, 所选12个剖面的垂向分布及其对应的经纬度和均方根误差如图12所示。所有剖面在混合层以上拟合效果明显比下层好, 并且大部分反演结果与观测剖面的偏差有随深度递增的趋势, 即, 随深度的加深, 反演结果的精度逐渐降低, 但即便是均方根误差较大的反演结果, 其与观测剖面的最大偏差也不超过2°C。其中, 南太平洋的观测剖面, 均方根误差普遍较小, 拟合效果最好; 赤道太平洋及北太平洋的观测剖面均方根误差相对较大, 特别是北太平洋的大部分反演结果与观测剖面的都大于1°C, 其拟合效果也较差, 这与图11得出的结论相一致。但反演结果与观测剖面总体上具有较好的一致性, 由此说明, 本文的计算结果比较接近实际观测, 具有一定的可靠性。

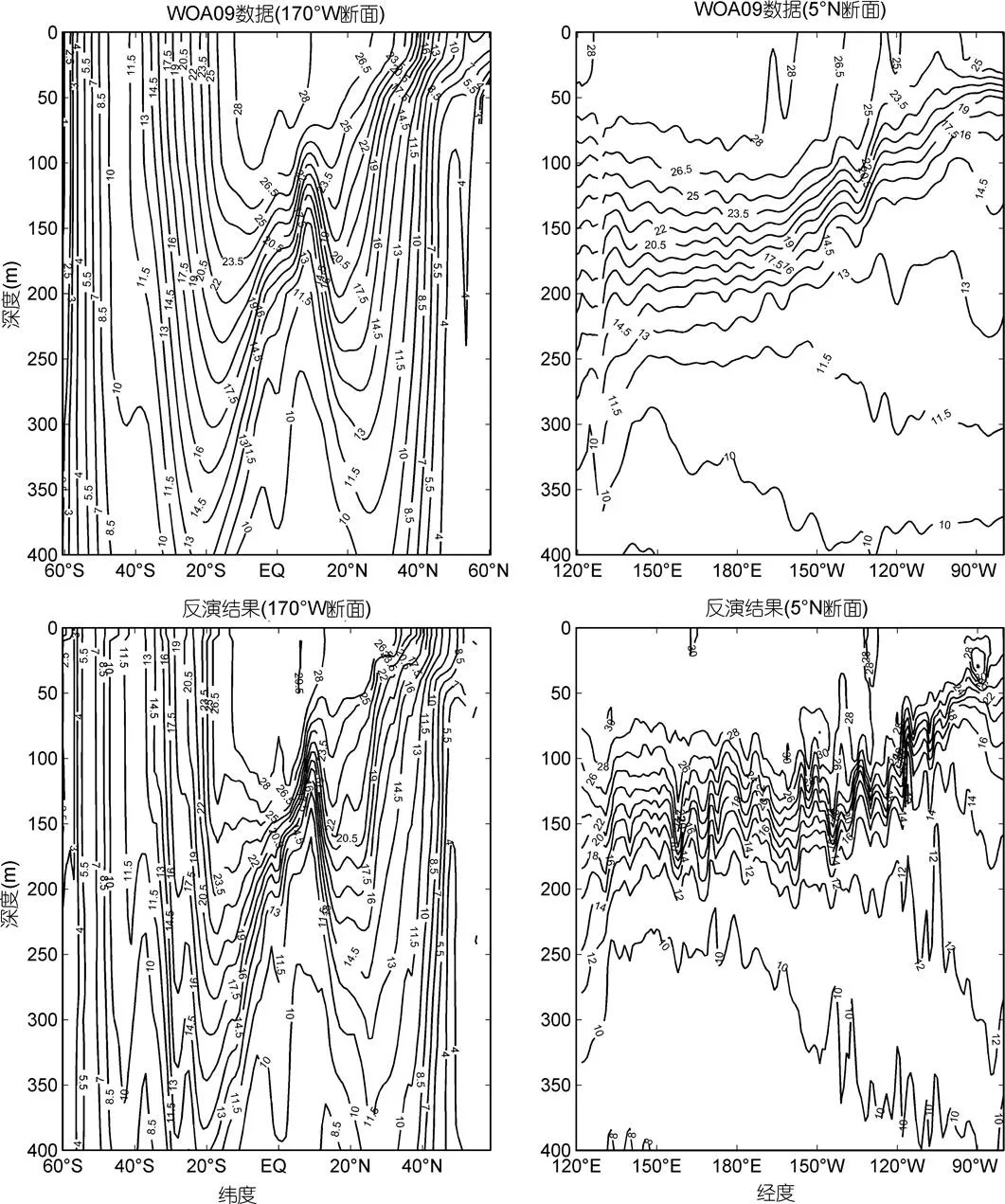
图8 170°W经线(左)及5°N纬线(右)温度断面分布

5 结论

利用卫星遥感获得的大范围、高分辨率、时间连续的海表信息, 借助已有的资料统计分析方法或数据同化方法等, 来构建三维温度场, 具有重要的实用价值。对Chu和Fan给出的温度参数模型, 本文借助-分布假设检验进行相关分析, 验证了其在太平洋海域的适用性, 进而利用卫星遥感海表温度观测数据, 在太平洋海域反演得到了2011年8月份的上层海洋三维温度场, 其空间分辨率为1°×1°。并基于Argo观测资料及WOA09气候态温度数据, 采用最大角度法确定三个关键参数: 混合层深度、温跃层梯度、温跃层下边界深度。以150m层温度场水平分布及两个温度断面为例, 定性分析了计算结果所反映的海洋现象。并通过与Argo观测剖面作对比, 定量计算了反演结果的精度。结果表明, 本文以2011年8月份太平洋为例, 反演得到的气候态三维温度场是可信、可靠的, 为实现现场观测(如: Argo)与卫星观测相结合提供一种新途径。

图9 太平洋海域150m层温度场

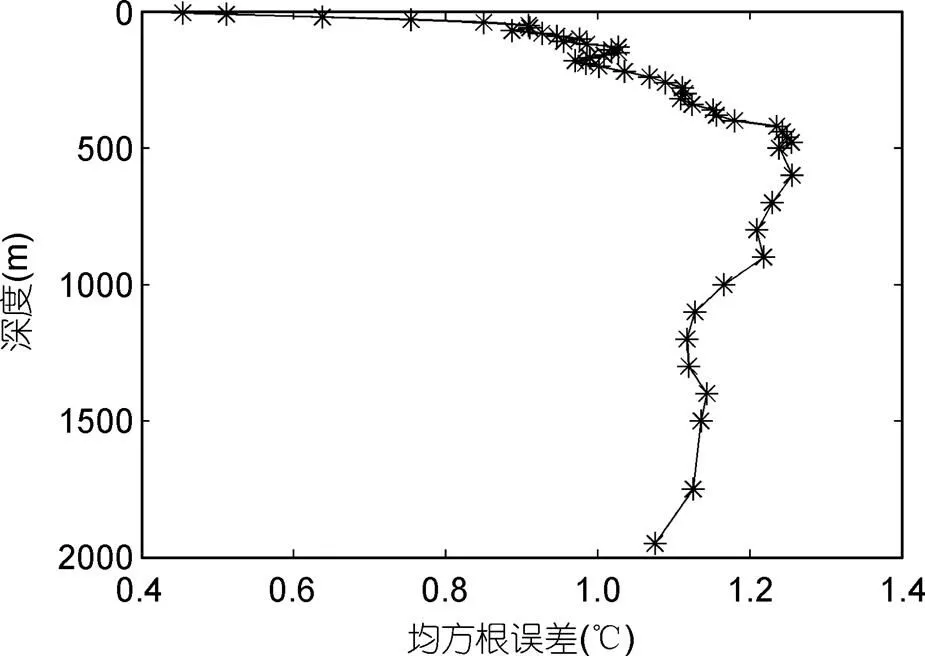
图10 均方根误差垂向分布曲线

本文在确定模型参数时采用了最大角度法, 此方法较以往确定混合层深度的方法(如: 梯度法, 曲率法)是一种客观、新颖的方法, 有较强的理论基础。由3.1节和3.2节的计算结果可以看出, 作者利用此方法得到的混合层深度是较符合实际的。但此方法的一个前提是分析变量具有严格的单调性, 文中作者忽略了障碍层的影响, 用密度混合层深度代替温度混合层深度, 势必会产生一定的误差。

在相关分析检验中, 作者借助-分布假设检验给出了相关系数的置信度。此结果是对整个太平洋海域做的统计分析, 因此, 证明本文采用的反演方法就整个太平洋海域来说, 具有一定的适用性。但不一定对每个小区域都具有很好的适用性, 该方法在混合层以下, 温跃层深度内利用简单线性拟合得到温度随深度的变化规律, 但实际温度变化并非随深度的增加而简单的线性递减, 因此在温跃层的海域, 拟合结果与实际有较大误差, 此外, 也有前人发现在东太平洋亚北极地区计算结果有较大的误差(Yan, 2004), 这些缺点仍需要进一步研究解决。但该方法在太平洋大部分海域仍有较好地适用性。

另外, 值得注意的是, 除海表温度以外, 海洋垂直剖面还与许多其他因素有关, 例如风速, 而本文仅利用海表温度信息, 通过由观测及历史数据确定的下层温度结构参数来反演次表层温度场, 这也是造成所获取的上层温度偏差空间不均匀的原因之一。故本文所反演的上层海洋三维温度场可用于海洋模式积分的初猜场, 从而缩短模式积分年限, 但直接用于分析海洋温度分布特征仍有较大的不足。

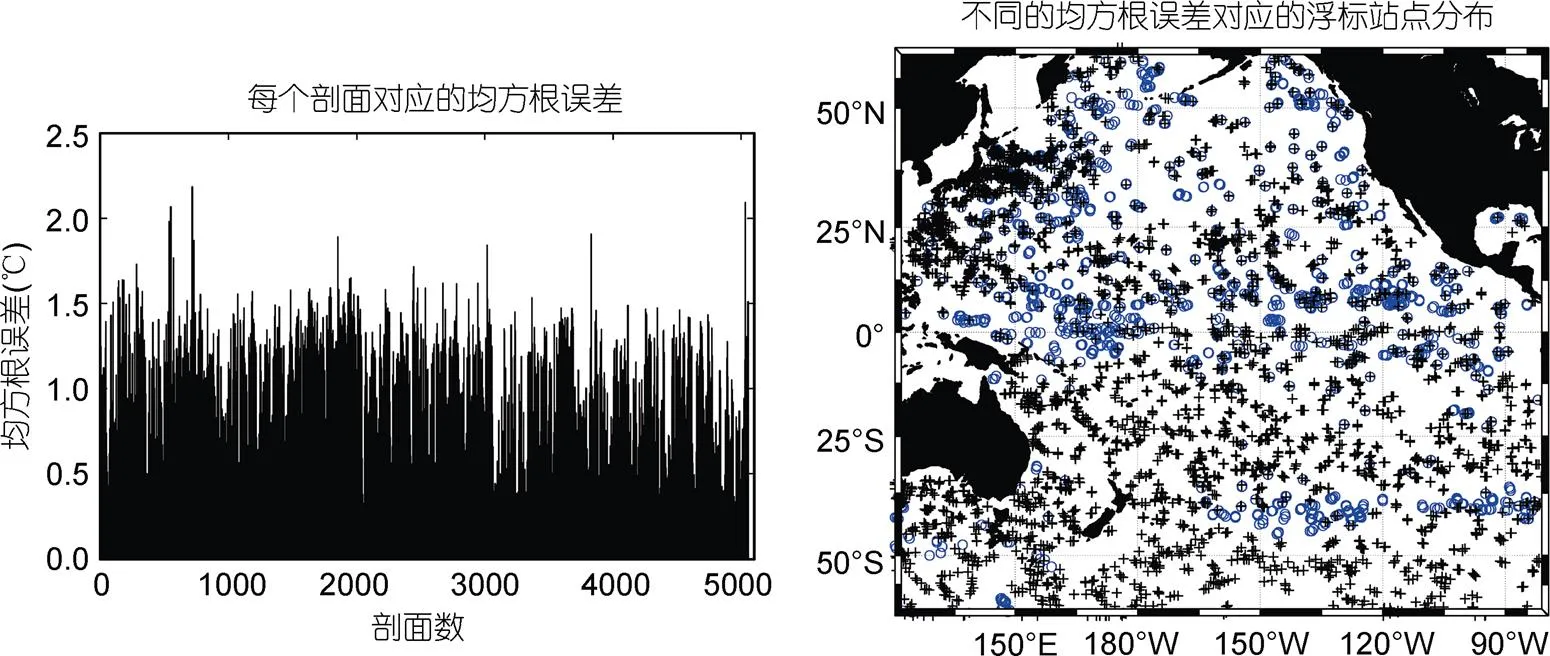
图11 反演结果与Argo观测剖面的均方根误差分布曲线(左)及不同均方根误差范围对应的站点分布(右)

＋: 误差小于1°C (3825个);○: 误差大于1°C (1241个)

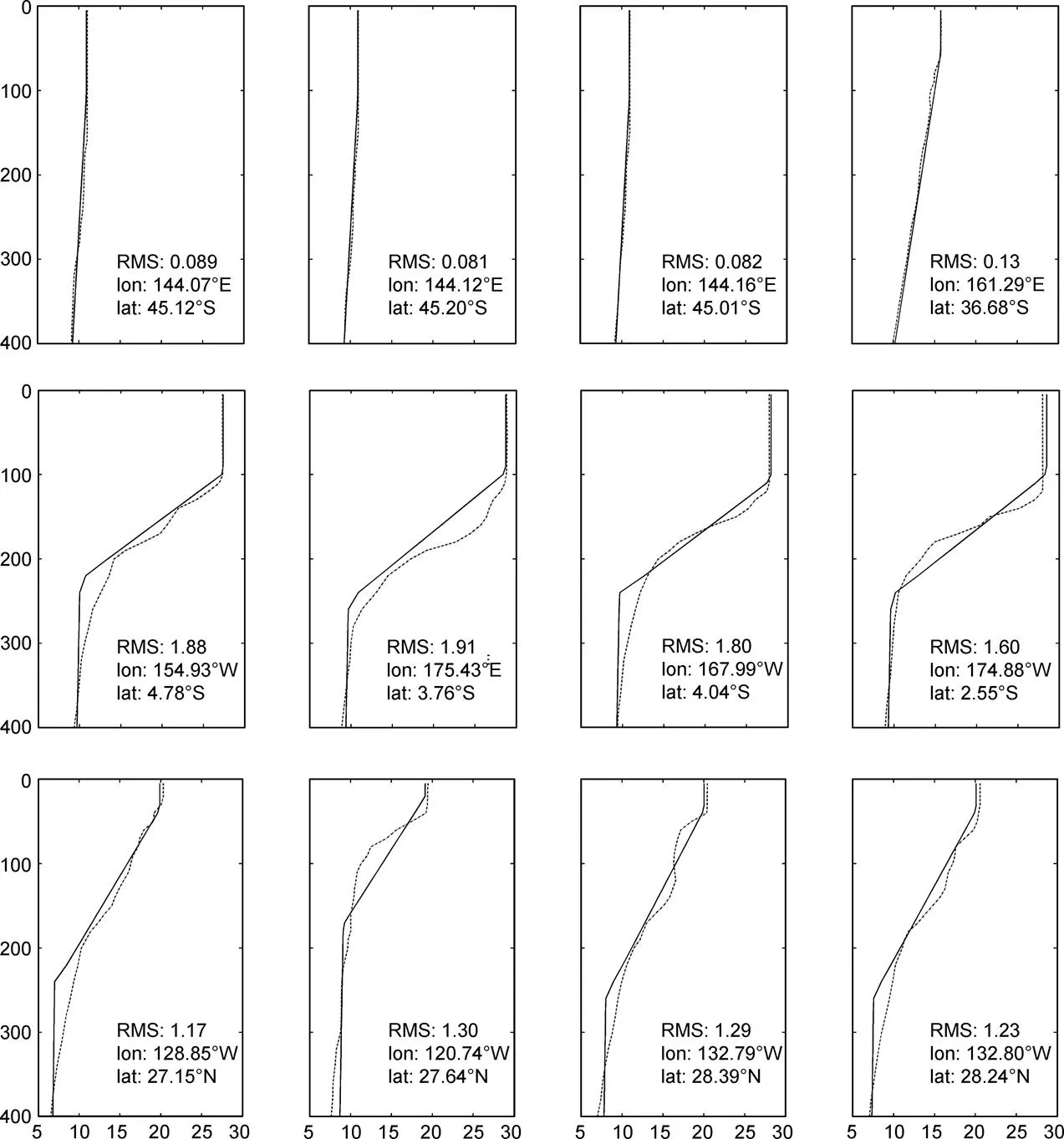
图12 反演剖面(实线)与观测剖面(虚线)的对比分布

致谢

美国海军研究生院的朱伯承教授为本文研究给予指导, 国家海洋局第二海洋研究所的同事们为本文提供了不可或缺的宝贵信息和资料, 谨致谢忱。

王彦磊, 黄 兵, 张 韧等, 2008. 基于Argo资料的世界大洋温度跃层的分布特征. 海洋科学进展, 26(4): 428—435

王喜东, 韩桂军, 李 威等, 2011. 利用卫星观测海面信息反演三维温度场. 热带海洋学报, 30(6): 10—17

芦 静, 乔方利, 魏泽勋等, 2008. 夏季海洋上混合层深度分布研究——Argo资料与Levitus资料的比较. 海洋科学进展, 26(2): 145—155

周燕遐, 李炳兰, 张义钧, 2002. 世界大洋冬夏季温度跃层特征. 海洋通报, 21(1): 16—22

Akima H, 1970. A new method for interpolation and smooth curve fitting based on local procedures. J Assoc Comput Mech, 17: 589—602

Behrinoer D W, Ming Ji, Ants L, 1998. An Improved Coupled Method for ENSO Prediction and Implications for Ocean Initialization. Part I: The Ocean Data Assimilation System. J Monthly Weather Review, 126: 1013—1021

Bruno B N, Santoleri R, 2004. Reconstructing synthetic profiles from surface data. J Atmos Oceanic Technol, 21: 693—703

Carnes M R, Mitchell J L, Dewitt P W, 1990. Synthetic temperature profiles derived from Geosat altimetry: Comparison with air-dropped expendable bathythermograph profiles. J Geophys Res, 95(C3): 17979—17992

Carnes M R, Teague W J, Mitchell J L, 1994. Inference of subsurface thermohlaline structure from fields measurable by satellite. J Atmos Oceanic Technol, 11: 551—566

Chu P C, Fralick C R, Jr S D, 1997a. A parametric model for the Yellow Sea thermal variability. J Geophys Res, 102: 10 499—10507

Chu P C, Tseng H C, Chang C P, 1997b. South China Sea warm pool detected from the Navy’s Master Oceanographic Observational Data Set (MOODS). J Geophys Res, 102: 15761—15771

Chu P C, Fan C W, 2000. Determination of Vertical Thermal Structure from Sea Surface Temperature. J American Meteorological Society, 17: 971—979

Chu P C, Fan C W, 2011. Maximum angle method for determining mixed layer depth from sea glider data. J Oceanogr, 67: 219—230

Fox D N, Teague W J, Berron C N, 2002. The modular ocean data assimilation system. J Atmos Oceanic Technol, 19: 240—252

Gavart M, Mey P, 1997. Isopycnal EOFs in the Azores Current region: A statistical tool for dynamical analysis and data assimilation. J Phys Oceanogr, 27: 2146—2157

Gavart M, Mey P, Caniaux G, 1999. Assimilation of satellite altimeter data in a primitive-equation model of the Azores-Madeira region. J Dyn Atmo Oceans, 29: 217—254

Guinehut S, Traon P-Yle, Larnicol G, 2004. Combining Argo and remote-sensing data to estimate the ocean three dimensional temperature fields——A first approach based on simulated observations. J Journal of Marine Systems, 46(1—4): 85—98

Hurlburt H E, 1986. Dynamic transfer of simulated altimeter data into subsurface information by a numerical ocean model. J Geophys Res, 91: 2372—2400

Hurlbtrt H E, Fox D N, Metzger J, 1990. Statistical inference of weekly correlated subthermocline fields from satellite altimeter data. J Geophys Res, 95: 11375—11409

Khedouri E, Szczechowski C, 1983. Potential oceanographic applications of satellite altimetry for inferring subsurface thermal structure. J Proc Mar Technol Soc, 83: 274—280

Pascual A, Gomis D, 2003. Use of surface data to estimate geostrophic transport. J Atmos Oceanic Technol, 20: 912—926

Thacker W C, Long R B, 1988. Fitting dynamics to data. J Geophys Res, 93(C2): 1227—1240

Tully J P, Giovando L F, 1963. Seasonal temperature structure in the eastern subarctic Pacific Ocean. Marine Distributions, M. J. Dunbar, ed. University of Toronto Press, 10—6

Witt P W, 1987. Modal decomposition of the monthly Gulf Stream/Kuroshio temperature fields. Technical Report, Naval Oceanographic Office, Stennis Space Center, 1—6

Yan C X, Zhu J, Li R, 2004. Roles of vertical correlations of background error and T-S relations in estimation of temperature and salinity profiles from sea surface dynamic height. J Geophys Res, 109, C08010, doi: 10.1029/2003JC002224

INVERSION OF SUBSURFACE THREE-DIMENSIONAL TEMPERATURE FROM REMOTE SATELLITE SEA SURFACE TEMPERATURE

ZHANG Chun-Ling1, 2, XU Jian-Ping1, 2, 3, BAO Xian-Wen1, WANG Zhen-Feng4,LIU Zeng-Hong2, 3, SUN Zhao-Hui2

(1. Institute of Marine Environment, Ocean University of China, Qingdao 266003, China; 2. Second Institute of Oceanography, State Oceanic Administration, Hangzhou 310012, China; 3. State Key Laboratory of Satellite Oceanography Environment Dynamics, Second Institute of Oceanography, State Oceanic Administration, Hangzhou 310012, China; 4. Marine Hydrologic Meteorological Center, East China Sea Fleet Command, Ningbo 312122, China)

A simple vertical thermal structure is proved applicable to the Pacific Ocean through correlation analysis test. Based on the Argo observations and WOA09 (World Ocean Atlas 2009) climate data, we determine the parameters by the maximum angle method. Then in the Pacific Ocean, a three-dimensional subsurface temperature field whose spatial resolution is 1o×1ois inversed from high-resolution sea surface temperature. Compared with the observational temperature profiles, the inversion result is reliable and can be assimilated into the system of the ocean reanalysis as pseudo temperature observation. That will provide a strong theoretical basis and solid data base for realizing complementary advantages of the situ observation (such as Argo) and the satellite observation, which is conductive to construct the complete temperature analysis field.

thermal parametric model; maximum angle method; Argo observation; SST; inversion

10.11693/hyhz20120928003

* 海洋公益性专项, 201005033号; 科技基础性工作专项, 2012FY112300号; 国家海洋局第二海洋研究所基本科研业务费专项, JT0904号。张春玲, 博士研究生, E-mail : zhangchunling81@163.com

2012-09-17,

2012-12-17

P731