白冠破碎空间分布模式的统计推断方法*
陈 佳 类淑河, 管长龙 张 冲 陶山山
白冠破碎空间分布模式的统计推断方法*
陈 佳1类淑河1,2①管长龙2张 冲1陶山山3
(1. 中国海洋大学数学科学学院 青岛 266100; 2. 中国海洋大学物理海洋实验室 青岛 266100; 3. 中国海洋大学工程学院 青岛 266100)
白冠空间分布模式分析是海浪破碎统计研究的前提。本文提出利用空间点过程统计分析工具研究白冠空间分布模式, 并结合实际白冠破碎观测录像资料, 计算观测数据的-函数和-函数, 与Markov chain Monte Carlo(MCMC)方法生成的模拟包迹进行比较, 推断得出其白冠空间分布模式类型为空间齐次Poisson过程。研究表明空间点过程统计分析工具适用于白冠破碎研究。
白冠破碎; 空间点过程;-函数;-函数; Markov chain Monte Carlo(MCMC)
海浪破碎是广袤海洋中最常见的一种自然现象。这种破碎是海-气间动量、能量传输和物质交换的重要渠道, 在海-气相互作用中扮演着主要角色。破碎会加剧海-气之间的气体交换, 产生的湍流对海洋上混合层各种物理过程有着显著影响破碎也是维持波浪场能量平衡、限制波高的主要机制(Melville, 1996; Asher, 1996)。此外, 海浪破碎研究对海洋遥感、海洋工程、导航和其他实际应用也有非常重要的作用。
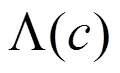
白冠破碎的发生具有很强的随机性, 破碎发生的时刻与位置都是随机的, 不同破碎的强度和空间规模也各不相同。人们至今对这种随机性的理解仍较肤浅。在实际观测资料处理中, 无论是白冠覆盖率, 还是破碎波波峰线长度, 大多仅仅停留于简单的求和或取平均。它们本质上只是对过程中某项真实参数的一种估计, 没有真正考虑破碎白冠的空间分布模式。若没有一个恰当的数学模型来描述这种随机性, 很难说清楚上面这些估计的可靠性与稳健性。
事实上, 空间点过程正是刻划白冠破碎随机性的恰当数学工具。空间点过程研究最早可追溯到20世纪60年代早期在地理学领域的研究, 研究者们将植物生态学中有关空间模式的分析方法应用到其它的领域中(Gatrell, 1996)。Ripley(1977)首次系统提出空间点模式分析的统计理论, 后经Diggle(2003)、Baddeley(2007)、Stoyan(2006)和Moller(2007)等统计学家的发展, 理论方法得到逐步完善, 形成了空间点过程的理论。近年来, 在地震学、生态学、森林学、地理学、空间流行病学以及材料科学等诸多领域获得成功应用(Moller, 2007)。目前国内外还没有见到采用空间点过程理论方法研究白冠破碎的文献。
如果将破碎白冠的重心位置视为平行于海面的二维平面上的点, 任一时刻在给定海域的白冠破碎形成一空间点过程。在这一理论框架下, 白冠面积、波峰线长度等特征量都可以视为过程的标值, 白冠覆盖率和L()可由累计的空间标值点过程描述。显然, 在空间点过程的理论框架下, 对于海浪破碎的随机性和破碎耗散等问题可以有更深入的理解和讨论。
白冠破碎空间分布模式(以下简称“白冠分布模式”)的统计推断正对应空间点过程类型的判断, 这是白冠破碎空间点过程模型研究的基本前提。空间统计学理论中的-函数、-函数等统计函数, 提供了空间点过程类型推断的有效工具(Loosmore, 2006; Baddeley, 2007)。本文借助这些工具, 讨论白冠破碎空间点分布模式的统计推断方法, 并以实际观测的破碎白冠图像分析为例, 演示推断过程, 讨论白冠破碎空间分布模式推断与结果分析中面临的问题。
1 空间点过程及其推断工具简介
1.1 空间点过程
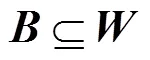
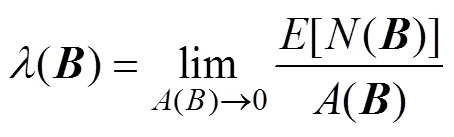
其中()表示区域的面积,[()]表示区域内点数的期望(Moller, 2007; Walter, 2005)。
空间点过程主要分为三类: 空间齐次Poisson过程、Cox过程和Gibbs过程。空间齐次Poisson过程具有空间完全随机性(complete spatial randomness, CSR), 其在任意有界空间区域内的事件数服从Poisson分布, 强度是常数, 不随空间区域变化。Cox过程由主过程和从属过程两级过程构成, 过程的强度不再是一个常数, 而是具有空间依赖性, 往往表现为点的簇生性(或称聚集性)。这类过程最早由Cox (1955)提出, 因而命名为Cox过程。Cox过程模型又可分为很多不同的具体模型(Moller, 2007)。Gibbs过程与Cox过程类似, 同样由两级过程组成, 是在空间齐次Poisson过程的基础上进行Gibbs取样而获得, 因此命名为Gibbs过程。在Gibbs过程中, 主要表现为过程内点之间的相互排斥性, 形成的过程具有规则分布的特点。Gibbs过程模型也分为很多具体类型(Baddeley, 2007; Ripley, 1977)。
1.2 基本统计推断工具介绍
空间点分布模式的统计推断的实质是由观测模式来推断点过程的类型。不同尺度下, 同一观测资料对应的点过程类型可能不同。因而推断工具与推断结论都要考虑研究尺度的选择。常用的推断工具为-函数和-函数, 它们都是研究尺度的函数(Loosmore, 2006; Stoyan, 2006)。-函数由Ripley(1977)提出, 通过计数测度()的等效二阶矩测度来定义(Baddeley, 2007)。当=(0,)((0,)表示以原点为圆心,为半径的圆域)时,
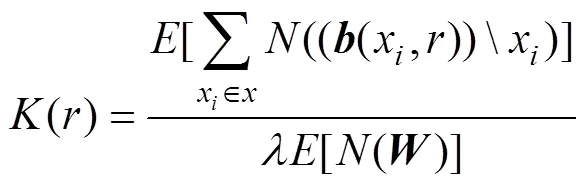
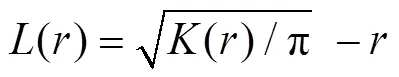
有了具体观测后,-函数可通过
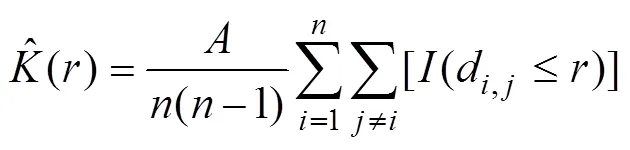
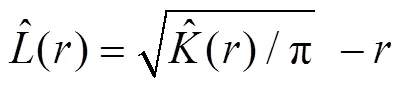
在计算这些统计函数的估计时, 接近边界的点, 会对计算结果产生一定的影响, 这种影响称为边界效应(Moller, 2007)。常用的修正方法有: 边界修正(Ripley, 1988)、平移修正(Ohser, 1983)和Ripley同质修正(Ripley, 1988; Ohser, 1983)。修正之后的-函数估计为:
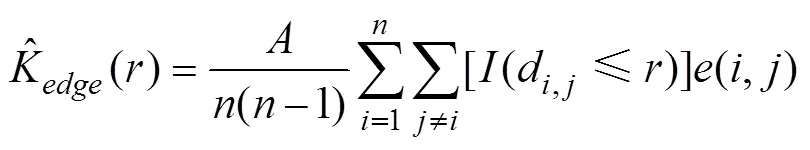
其中(,)为边界修正项。
2 白冠分布模式统计推断方法示例
2.1 图像识别
图1为一实际观测的白冠破碎图像, 选自我们在青岛大公岛西部海域(35°59′10.822″N, 120°25′53.190″E)录像资料, 拍摄时间为2011年4月, 当时平均风速在5m/s左右, 东南风, 采用Sony CX180摄像机拍摄, 25帧/秒。由于拍摄具有一定的倾角, 图像产生透视失真, 处理前先使用photoshop粗略校正, 而后采用Kleiss(2009)提出的白冠识别方法, 以图像中每个显著白冠的重心位置作为事件发生点(忽略面积小于50像素的破碎), 形成观测模式, 如图2所示。
2.2 白冠分布模式的统计推断
图3给出了白冠观测模式的-函数图像。研究尺度的选择借鉴Diggle的建议, 不超过观测区域最短边的1/3(Diggle, 2003)。图中点状虚线为空间齐次Poisson过程(CSR假定)的理论函数值, 实线为观测模式的-函数估计值, 线段状虚线代表999次CSR模拟模式产生的上、下界。当>1时, 尽管观测模式的-函数位于()=0的上方, 但仍完全落入上、下界所确定的范围内部, 无法拒绝白冠破碎的空间分布模式为CSR模型的零假设。

图1 实际白冠破碎图像
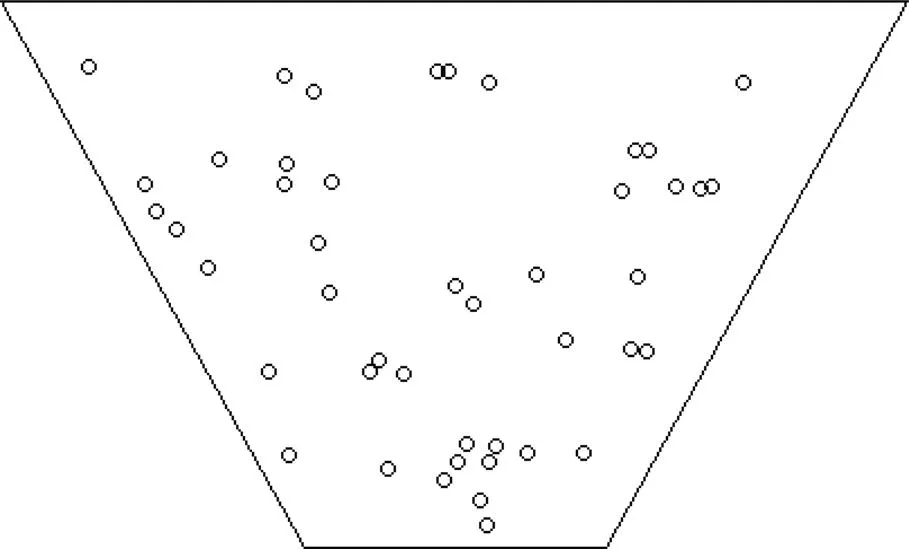
图2 白冠破碎(圆圈)的观测模式
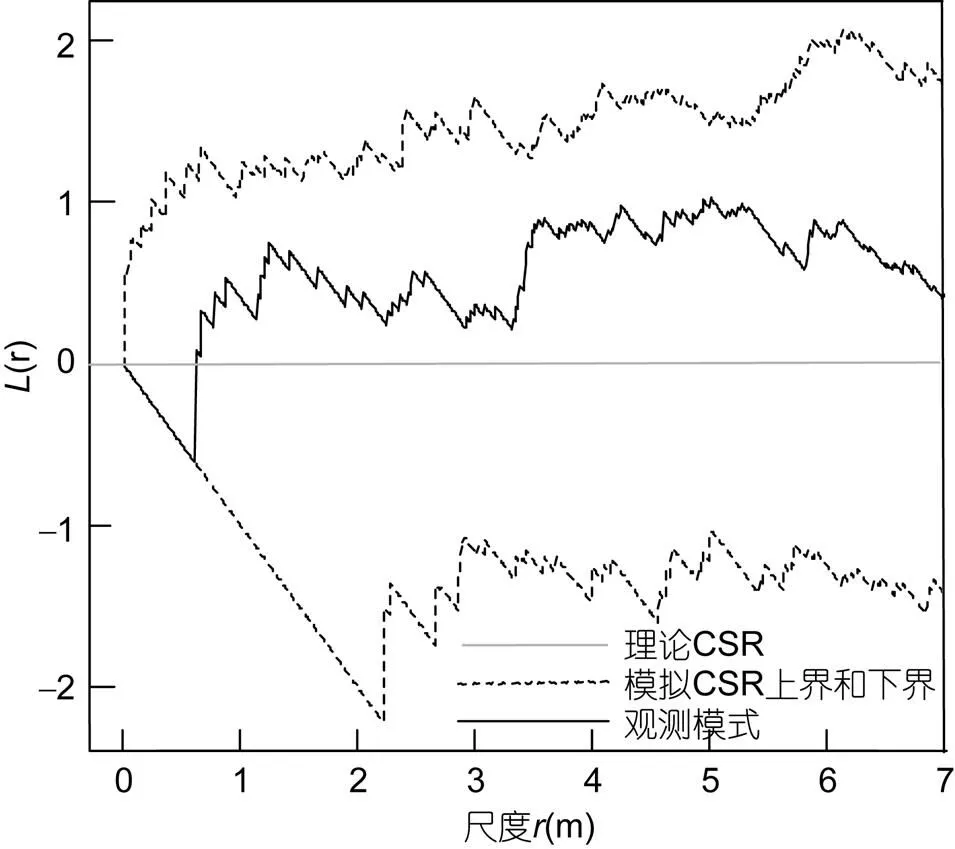
图3 观测模式的L-函数估计图像
上述基于-函数对空间点过程类型的判断只是初步的, 更严格的推断一般采用Markov chain Monte Carlo(MCMC)方法实现模拟包迹检验。MCMC方法不仅用于生成所选择的模型, 也用于进行模型检验和参数估计(Stoyan, 2006)。由于Cox过程和Gibbs过程的模型有多种类型, 其-函数和-函数的理论结果往往未知, 不适合作零假设模型。因而检验中零假设通常采用空间Poisson过程(CSR假定)。
在每次模拟中, 我们基于MCMC方法产生999次的来自CSR模型的模拟模式。分别计算观测模式与模拟模式的-函数, 以模拟模式的值来形成-函数的拟合包迹, 如图4中灰色带状区域所示, 实线为依据观测模式计算的-函数, 点状虚线为空间齐次Poisson(CSR)理论-函数曲线。观察观测模式-函数估计与拟合包迹的相对位置: 如果在每一个研究尺度上, 观测模式的估计均位于拟合包迹区域内部, 则认为观测模式具有完全随机性, 不拒绝空间齐次Poisson过程的假设; 如果在某一个研究尺度上, 观测模式估计落在包迹区域的上方, 则认为实际观测对应的过程为Cox过程类; 若落在包迹区域下方, 则认为实际观测对应的过程为Gibbs过程类。
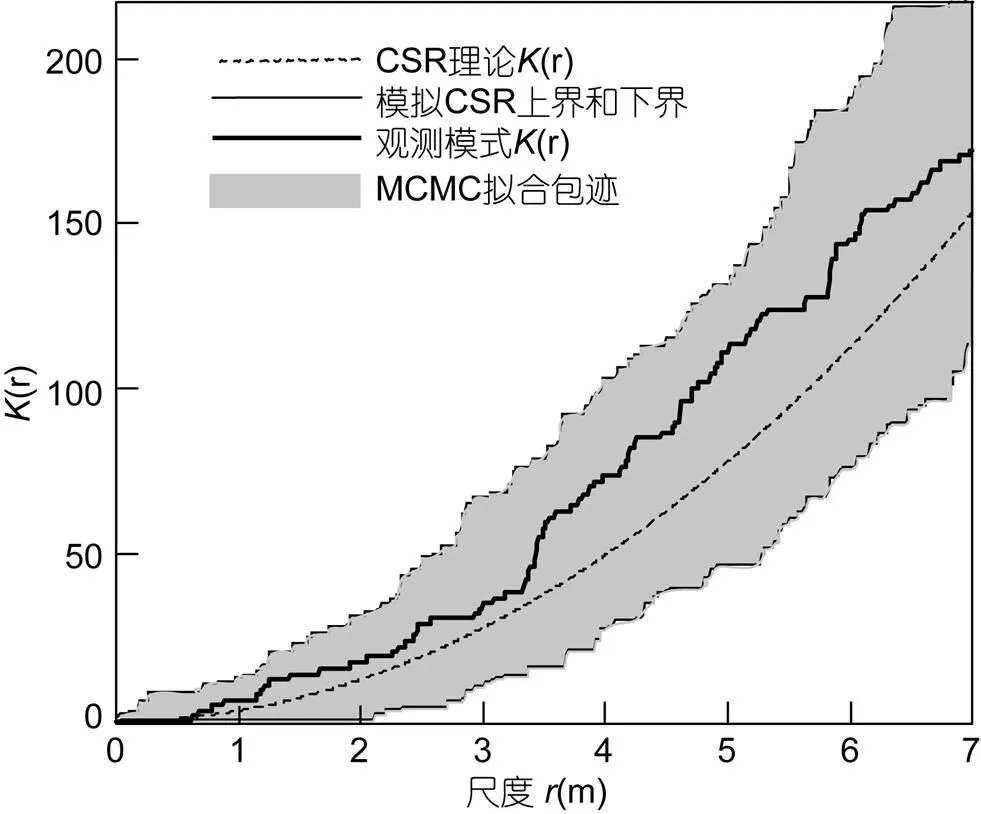
图4 观测图像K-函数与CSR模拟包迹
从图4可以看出, 在我们选择的尺度范围内, 观测模式-函数图像尽管在>1时位于空间齐次Poisson过程的上方, 却均落在拟合包迹(灰色)区域的内部。这与图3给出的-函数结果一致, 因而我们可以认为, 在这些尺度上白冠分布模式为空间齐次Poisson过程类型。
3 结论及讨论
本文借助空间点过程的理论及其推断工具, 包括-函数和-函数, 提出了白冠分布模式的统计推断方法, 并结合白冠图像数据, 验证了方法的可行性和有效性。通过实例展示, 我们认为白冠破碎空间点分布模式的统计推断方法可用于白冠破碎的研究。
由于拍摄时摄像机具有一定的倾角, 使得图像产生透视失真, 从而使得这些距离也失真。这对于-函数、-函数估计的计算是有影响的, 因为这些计算都是基于事件发生点之间的距离进行的。因而, 图像校正是图像预处理中的关键环节。本文只是使用photoshop进行较为粗略的校正, 还有待于进一步改进校正方法。在使用Kleiss(2009)提出的识别方法提取破碎白冠的重心坐标时, 阈值的设置也会使识别过程中遗漏或误判小的白冠破碎, 这些都可能影响到推断结果的可靠性。
另外, 空间点分布模式的推断结果也依赖于分析尺度。限于摄像设备与拍摄点的高度, 录像资料所覆盖的区域有限, 因此我们目前的研究仅局限于较小的区域范围(100m以内), 更大分析尺度下的点分布模式仍是未知的。因而, 文中的推断分析仅仅作为白冠破碎空间点分布模式的统计推断方法应用于白冠破碎随机性研究。推断结果是否可靠, 依赖于白冠破碎图像校正与识别方法的改进。
Alcock R K, Morgan D G, 1978. Investigation of wind and sea state with respect to the Beaufort scale. Weather, 33(7): 271—277
Asher W E, Karle L M, Higgins B J, 1996. The influence of bubble plumes on air-seawater gas transfer velocities. Journal of Geophysical Research, Oceans (1978—2012), 101(C5): 12027—12041
Baddeley A, 2007. Spatial Point Processes and their Applications. In: Weil W ed. Stochastic Geometry. Sringer, Berlin: 1—75
Besag J, 1977. Discussion of Dr Ripley’s paper. Journal of the Royal Statistical Society, Series B, 39: 193—195
Cox D R, 1955. Some statistical models related with series of events. Journal of the Royal Statistical Society, Series B, 17: 129—164
Daley D J, Vere-Jones D, 2002. An introduction to the theory of point processes: Volume 1: Elementary Theory and Methods, 2nd edn. Springer-Verlag, New York, USA: 1—65
Daley D J, Vere-Jones D, 2002. An introduction to the theory of point processes: Volume 2: General Theory and Structure, 2nd edn. Springer-Verlag, New York, USA: 457—536
Diggle P J, 2003. Statistical analysis of spatial point patterns, 2nd edn. Edward Arnold Publishers, London, UnitedKingdom: 1—62
Gatrell A C, Bailey T C, Diggle P J, 1996. Spatial point pattern analysis and its application in geographical epidemiology. Transactions of the Institute of British Geographers, New Series, 21(1): 256—274
Guan C L, Hu W, Sun J, 2007. The whitecap coverage model from breaking dissipation parametrizations of wind waves. Journal of Geophysical Research, 112, C05031: 1—9
Isham V, 1981. An Introduction to Spatial Point Processes and Markov Random Fields. International Statistics Review, 49(1): 21—43
Kleiss J M, 2009. Airborne observations of the kinematics and statistics of breaking waves. San Diego: Ph. D. of University of California.
Loosmore N B, Ford E D, 2006. Statistical inference using the G or K point pattern spatial statistics. Ecology, 87(8): 1925—1931
Melville W K, 1996. The role of surface-wave breaking in air-sea interaction. Annu Rev Fluid Mech, 28: 279—321.
Melville W K, Kleiss J M, 2011. Spectral Energy Dissipation due to Surface-Wave Breaking. Journal of Physical Oceanography, 42(9): 1—60
Moller J, Waagepetersen R P, 2007. Modern statistics for spatial point processes. Scandinavian Journal of Statistics, 34(4): 643—684
Monahan E C ,1969. Fresh water whitecaps. Atmos, 26: 1026—1029
Ohser J, 1983. On estimators for the reduced second moment measure of point processes. Mathematische Operationsforschung und Statistik, series Statistics, 14: 63—71
Phillips O M, 1985. Spectral and statistical properties of the equilibrium range in wind-generated gravity waves. J Fluid Mech, 156: 505—531
Ripley B D, 1977. Modelling Spatial Patterns. Journal of the Royal Statistical Society, Series B(Methodological), 39(2): 172—212
Ripley B D, 1988. Statistical inference for spatial processes. Cambridge University Press, London, UnitedKingdom
Stoyan D, 2006. Fundamentals of Point Process Statistics. Lecture Notes in Statistics, 185: 3—22
Walter C, McBratney A B, Viscarra Rossel R A, 2005. Spatial point-process statistics: concepts and application to the analysis of lead contamination in urban soil. Environmetrics, 16: 339—355
statistical inference methods FOR spatial point pattern of white-cap breaking
CHEN Jia1, LEI Shu-he1,2, GUAN Chang-long2, ZHANG Chong1, TAO Shan-shan3
(1. The College of Mathematics, Ocean University of China, Qingda, 266100, China; 2. The Laboratory of Physical Oceanography, Ocean University of China, Qingdao, 266100, China; 3. The College of Engineering, Ocean University of China, Qingdao,266100, China)
For a long time, research on white-cap breaking does not involve the issue of spatial distribution pattern. However, the spatial distribution pattern is the premise of research for describing the statistical characteristic of breaking waves. By applying the theory of spatial point process with statistical inference tools, we studied white-cap breaking and modeled its spatial distribution. Combining with the real white-cap breaking images, we calculated the-function and the-function of the observed patterns, and used MCMC (Markov chain Monte Carlo) random simulation test against the null hypothesis about homogeneous Poisson process, making the-function as basic statistics for inferring that the spatial point pattern of the observed images we chose is homogeneous Poisson process. Case studies show that the statistical tools of spatial point process can be applied effectively for research on white-cap breaking.
white-cap breaking; spatial point process;-function;-function; Markov chain Monte Carlo(MCMC)
10.11693/hyhz20121023001
* 国家自然科学基金重点项, 41276010号。陈佳, Email: cj_ouc@163.com
类淑河, 副教授, Email: shuhelei@ouc.edu.cn
2012-10-23,
2013-01-05
P731.22

