Research on Band Structure of One-dimensional Phononic Crystals Based on Wavelet Finite Element M ethod
Jiawei XiangHaifeng GaoYongying JiangYuqing Zhou
1 Introduction
Phononic crystals(PCs)are artificial materials with a periodic structure and were first investigated in the early seventies of the last centenary.The study of wave propagation in periodic structures has originated many novel discoveries in physics.Since the 1990s,there has been a great deal of work devoted to the study of phononic crystals[Kushwaha et al.(1993);Tarasenko et al.(2004)].The existence of phononic BGs where the propagation of acoustic or elastic waves is forbidden exhibits a lot of potential applications,such as noise reduction,waveguides,acoustic filters,etc.Therefore,the mechanism for tuning the band gap is always an important topic of the theoretical studies of PCs.
One of the most major content of phononic crystals is its band structure calculations.There are several numerical methods to calculate band structures.The plan-wave expansion(PWE)[Kushwaha et al.(1994);Tanaka and Tamura(1999)]is a powerful tool to investigate wave propagation problems and band structures.However,to deal with the problems of varied material parameters of components,the convergence is slow.Besides,when the classical PWE method is employed to solve fluid-solid PCs,the fictitious transversal modes are often occurred.Therefore,the extended PWE(EPWE)technique was presented to calculate fluid-solid PCs[Moiseyenko and Laude(2011)].Morover,the finite-difference time-domain method(FDTD)was developed to obtain the unique solutions of PCs with nonlinear material properties in a natural way[Tanaka and Tamura(1998)].However,FDTD can not be applied to PCs structures with complex geometry.Finite element method(FEM)is suitable to solve structural mechanics problems in complicated domains and then introduced to calculate band gaps(BGs)of PCs[Assouar and Oudich(2011)].FEM models of PCs lead to an eigenvalue problem,which is usually solved for the unknown frequencies(ω)with a real wave number(k),i.e.,theω(k)technique[Assouar and Oudich(2011)].Recently,boundary element method is proposed to solve band gaps of PCs with good performance[Gao et al.(2013a,2013b)].
Wavelet finite element method(WFEM)is developed in recent years as a new numerical method using scale function or/and wavelet function to replace the traditional polynomial as approximating function.Ko et al.constructed a class of one-dimensional wavelet based element by using orthogonal Daubechies wavelet[Ko et al.(1997)];Chen et al.proposed wavelet-based elements using Daubechies wavelet,B-spline wavelet wavelet on the interval(BSW I)respectively to analysis structural problems and developed adaptive WFEM[Chen et al.(2004,2010,2012)];Hang etal.extended the WFEM by using mixed variational principle[Hang et al.(2005,2006)];He and Ren continued to develop WFEM[He and Ren(2013a,2013b)].By utilizing multi-resolution characteristics,we can obtain a variety of wavelet-based elements to solve partial differential equations(PDEs)in engineering.Since BSW I scale functions at all level have the analytical expression,the elemental stiffness and mass matrices can be calculated conveniently[Xiang et al.(2007,2008a,2008b)].Therefore,the wavelet finite element method has been successfully applied to solve stress intensity factor[Xiang et al.(2012)]and damage detection field[Xiang and Liang(2011),Xiang et al.(2011),Li and Dong(2012),Li and He(2013)].Furthermore,for one-dimensional structures there have been applications of WFEM for curved beams[Yang et al.(2014)]and wave motion analysis in arch structures[Yang et al.(2014)].For two-dimensional structures,the vibration analysis of curved shell[Yang et al.(2012)]and free vibration and buckling analysis of plates[Yang et al.(2013)]are investigated using WFEM.Recently,WFEM was summarized by Li and Chen and the classification and further research directions were given[Li and Chen(2014)].Therefore,the WFEM is an effective numerical simulation method in structure analysis.
In this paper,we employed the wavelet-based element to construct FEM model of one-dimensional phononic crystals(1DPCs).The numerical dispersion relation of 1DPCs will be presented and it w ill be shown that for rational wave vectors,a Polynomial eigenvalue problem w ill be obtained.The BGs of 1DPCs are calculated using BSW I elements at different wavelet level.The results are verified and compared with the traditional finite element method.
2 WFEM model of 1DPCs
BGs for periodic structures are usually calculated in the frequency domain by utilizing unit cells and periodic boundary conditions(BCs).The same principle will be followed in the presented paper to investigate 1DPCs using wavelet-based element.Fig.1 shows the schematic structure of 1DPCs made of a series of identical segments.Each segment includes two differential materials forAandB(AandBhave the same cross-section)with their thickness area1anda2,respectively.The thickness(lattice constant or periodic distance)of a unit cell(lattice constant)isa=a1+a2.
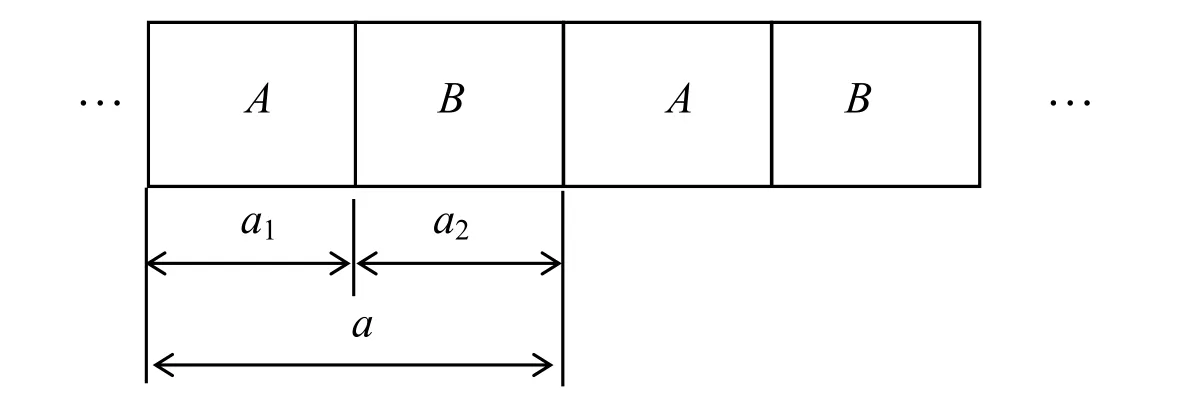
Figure 1:Schematic structure of 1DPCs.
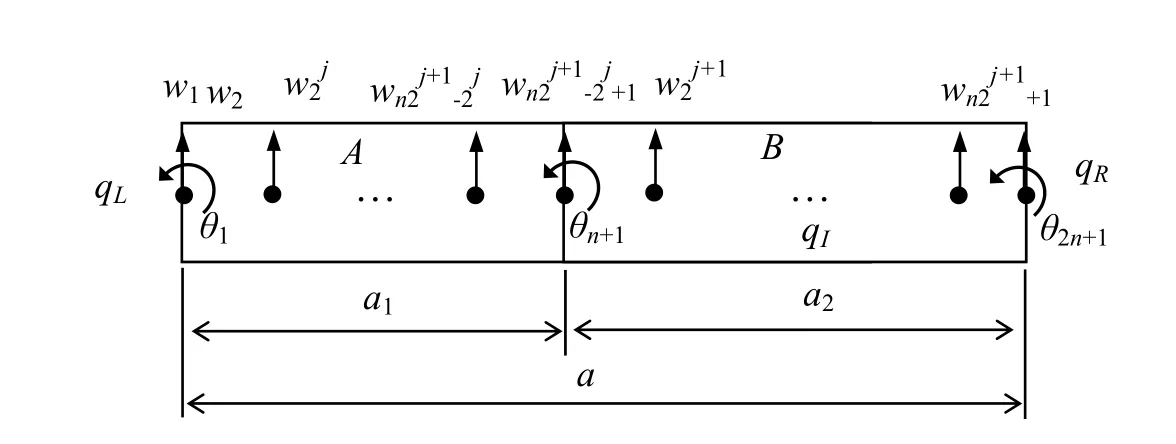
Figure 2:The diagram of a segment represented by 2n BSW I4j elements.
Fig.2 shows a unit cell of the structure.Consider the periodic characteristic,we can solve the band structure only using a unit cell of 1DPCs.Therefore,we focus on the calculation model using wavelet-based element on a unit cell.Suppose 2nBSW I4j(4 is the order of BSW I bases[Xiang et al,(2008a)],jis the wavelet level)Euler beam elements[Xiang et al.(2007)](nelements supported on sectionAand the othernelements supported on sectionB)are employed to discretize the unit cell,the degrees of freedom(DOF)corresponding to the node on the left hand boundaryqListhe node on the right hand boundaryqRisvR=and the other inner nodes is
Thus,the total DOF of a unit cell is

Corresponding to DOF in a unit cell,there will be a generalized force as[Veres and Berer,(2012)]

whereFL,FRandFIare the generalized force on the left hand boundary,the right hand boundary and the other inner nodes.
When a free wave propagates through an in finite structure,FIis zero.At this point,the periodic boundary conditions are not yet applied.Therefore,according to Bloch-Floquet theorem,the propagation constants between the nodes on left and right hand boundaries(exterior nodes)of a unit cell are given aseika(kis the wave number andiis the imaginary unit).The generalized forces at the exterior nodes,i.e.,FLandFR,are not zero,since these forces are responsible for transmitting the wave motion.
BecausevLandvRare separated by the periodic distancea,the relationship of the two DOF on the exterior nodes can be represented by[Veres and Berer(2012)]
让学生自己当家作主,做班集体的主人,相信他们,多给他们一些耐心与信心,多给他们一些鼓励与支持,静待花开。

similarly,the correspondingFLandFRshould have the relationship as

Therefore,the equation of motion of a unit cell(periodic section)is[Veres and Berer(2012)]
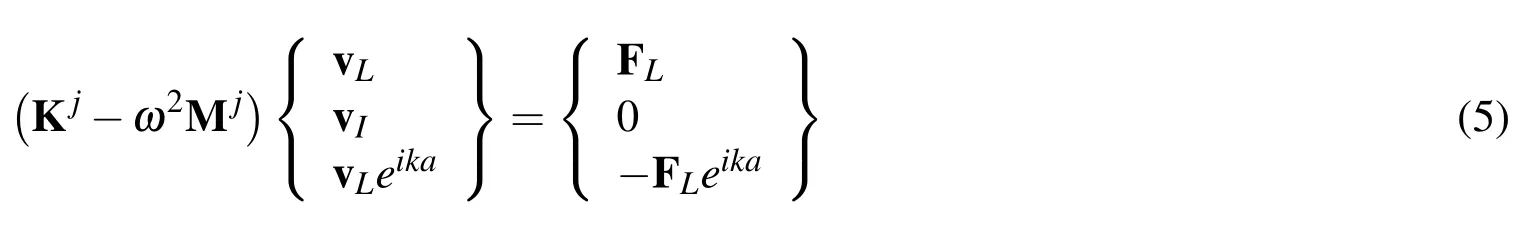
whereωis the angular frequency(rad/s),andare the global stiffness and mass matrices of a unit cell and the corresponding superscriptsjare also the wavelet level.
Because a unit cell consist of 2nBSW I4jEuler beam elements,andare formed by superposition of(the superposition of BSW I4jEuler beam element stiffness matricesof sectionA)and(the superposition of BSW I4jEuler beam element stiffness matricesof sectionB),(the superposition of BSW I4jEuler beam element mass matricesof sectionA)and(the superposition of BSW I4jEuler beam element mass matricesof sectionB).The BSW I4jEuler beam element stiffness and mass matricesandare[Xiang et al.(2007)]

in whichE1andE2,ρ1andρ2are the Young’s moduli and material densities of the two sectionsAandB,respectively,IandSare the moment of inertia,the area of cross-section for the two sectionsAandB,respectively,andare the column vector combined by the BSW I scaling functions for 4thorder at the levelj,the transformation matrices,respectively,as[Xiang et al.(2008a)]
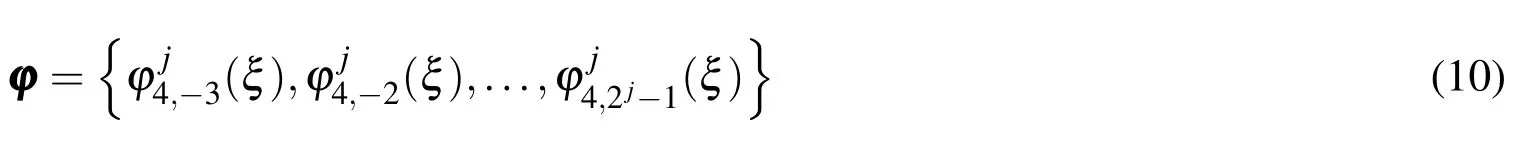

in which r=2jand the scaling functionsare shown in.[Xiang et al.(2008a)].
To simple the calculation,the global stiffness and mass matrices are partitioned to nine sub-blocks in associated with the three types of nodes,i.e.,a node on the left hand boundary,a node on the right hand boundary and nodes on the interior.Thus,we have

and

where L=2,I=n2j+1+2n−2,R=2.
In the present,we only calculate the band structure of PCs.Therefore,the generalized force matrix becomes zero and the equation of free vibration is

According to[Mead et al.(1973)],submitting Eq.(3)into Eq.(15),we have
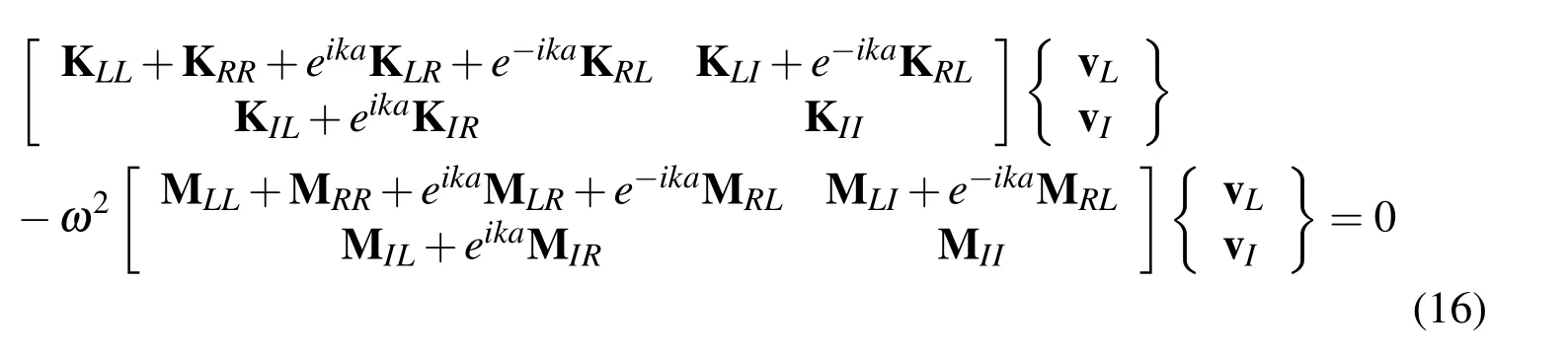
By separating real and imaginary parts[Wilkinson(1965)]and letandEq.(16)becomes
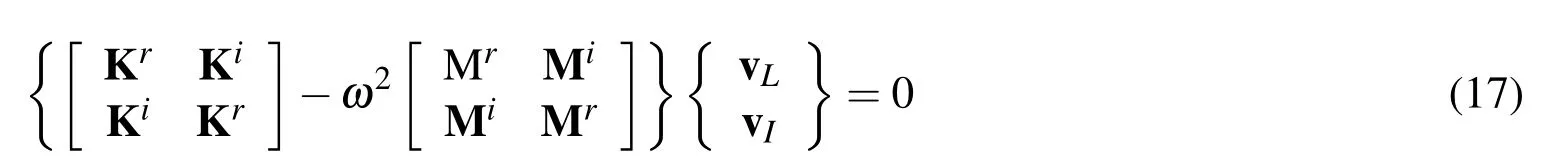
The corresponding free vibration frequency equation is

Let the matrices

Eq.(18)becomes

Eq.(21)represents a symmetric eigenvalue problem relatingkandωfor the discretised structure,whose solutions give WFEM estimates of the dispersion relations for the continuous structure.Corresponding to each value ofkin Eq.(21),there w ill be a discrete set of frequencies that occur in equal pairs.Each frequency will have associated with correspondence an eigenvector.This eigenvector defines the wave motion in the periodic section at that frequency.
3 Numerical investigation
As shown in Fig.1,we investigate PCs composed of copper(segmentA)and epoxy(segmentB)arranged in a lattice with a filling fractiona1:a2=1:1 and the lattice constanta=150mm.Table 1 shows the material parameters of copper and epoxy.

Table 1:Materials properties

Figure 3:The band structure of WFEM(squares)and traditional FEM(dashed and solid lines)
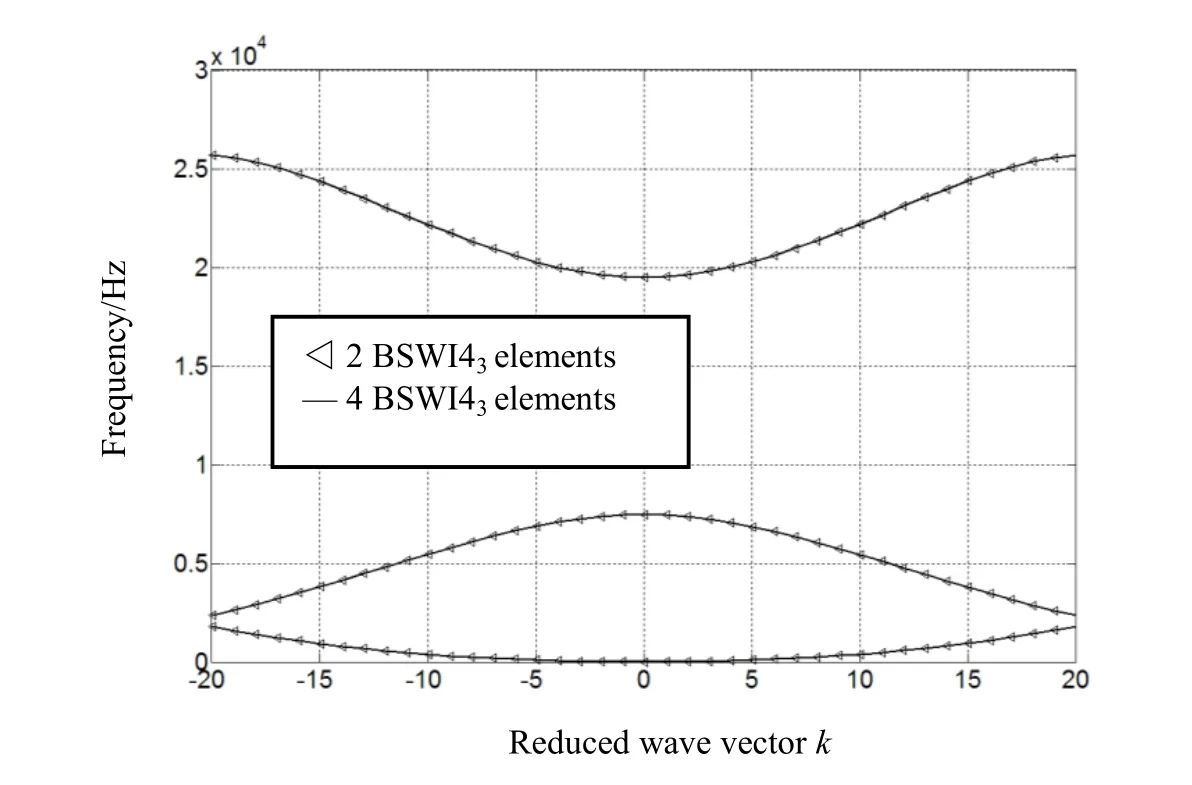
Figure 4:The band structure calculated by 2 and 4 BSW I43 Euler beam elements
In order to verify the validity of the present method,we employ 2 BSW I43Euler beam elements(20 DOFs),4 and 16 traditional Euler beam elements[Zienkiew icz et al.(2005)](10 and 34 DOFs)to solve the band structure of the 1DPCs.The results are plotted in Fig.3 and the squares,the dashed lines and the solid lines denote the solutions of 2 BSW I43Euler beam elements,4 and 16 traditional Euler beam elements,respectively.From Fig.3,we find that the results from the two methods are in good agreement and the 2 BSW I43Euler beam elements can reach the accuracy of 16 traditional beam elements.As well known,FEM is efficient and reliable to compute 1DPCs,which verifies that the developed WFEM can yield accurate results.It points out that the DOF used for traditional element more than 1.5 times of that of the present method.
The above results indicate that good calculation accuracy can be achieved for the 1DPCs by the proposed WFEM.The main advantage of the proposed method is the time savings due to the reduction of DOF.
To testify the convergence of the present wavelet FEM,we adopted 2(20 DOFs)and 4(38 DOFs)BSW I43Euler beam elements to calculate the BGs of 1DPCs,respectively.The results are shown in Fig.4.The solution of 2 elements also can reach high precision.This is because the resulting matrices are very sparse in the wavelet-based method.
Furthermore,we give a performance comparison of BSW I Euler beam element at different wavelet level,i.e.,BSWI43,BSW I44,BSW I45and BSW I46Euler beam elements.The results are basically identical with BSW I43.It illustrates BSW I43elements can gain a high accuracy to calculate the band structure.
The numerical results are presented in this paper demonstrating the accuracy,efficiency and reliability of the BSW I beam element.The fundamental cause of the good performance of BSW I beam element lies in the BSW I scaling functions with the advantages of high approximation precision and the excellent localization characteristic in space domain.
4 Conclusions
In this paper,the good approximation capability of BSW I4jbeam element has been explored to approximate the displacement fields of 1DPCs.More specifically,two BSW I4jbeam element are employed to discretize a unit cell and the corresponding equation of motion and further the corresponding frequency equation for calculating BGs are obtained.The numerical results show that the advantage of this method is its computational efficiency.This is reflected by the fact that it requires fewer elements,in comparison to the popular finite element method,to achieve the same solution quality.The further work is to compute BGs of 2D or 3D phononic crystals.
Acknowledgement:The authors are grateful to the support from the National Science Foundation of China(No.51175097),the Zhejiang Provincial Natural Science Foundation for Excellent Young Scientists(No.LR13E050002)and the Project-sponsored by SRF for ROCS,SEM.
Assouar,M.B.;Oudich,M.(2011):Dispersion curves of surface acoustic waves in a two-dimensional phononic crystal.Appl.Phys.Lett.vol.99,no.12,123505.
Chen,X.F.;Yang,S.J.;M a,J.X.;He,Z.J.(2004):the construction of wavelet finite element and its application.Finte Elem.Anal.Des,vol.40,no.5,pp.541-554.
Chen,X.F.;Xiang,J.W.;Li,B.;He,Z.J.(2010):A study of multiscale wave let based elements for adaptive finite element analysis.Adv.Eng.Softw,vol.41,no.2,pp.196-205.
Chen,X.F.;Yang,Z.B.;Zhang,X.W.;He,Z.J.(2012):Modeling of wave propagation in one-dimension structures using B-spline wavelet on interval finite element.Finite Elem.Anal.Des,vol.51,pp.1-9.
Gao,H.F.;M atsumoto,T.;Takahashi,T.;Isakari,H.(2013a):Analysis of band structure for 2D acoustic phononic structure by BEM and the block SS method.CMES-Comput.Model.Eng.Sci.,vol.90,pp.283-301.
Gao,H.F.;M atsumoto,T.;Takahashi,T.;IsakariH.(2013b):Eigenvalue analysis for acoustic problem in 3D by boundary element method with the block Sakurai-Sugiura method.Eng.Anal.Bound.Elem.,vol.37,pp.914-923.
Hang,J.G.;Ren,W.X.;Huang,Y.(2005):A multi variable wavelet based finite element method and its application to thick plates.Finte Elem.Anal.Des,vol.41,pp.821-833.
Hang,J.G.;Ren,W.X.;Huang,Y.(2006):A spline wavelet finite-elementmethodin structural mechanics.Int.J.Num.Meth.Engng,vol.66,pp.166-190.
He,W.Y.;Ren,W.X.(2013a):Adaptive trigonometric herm ite wavelet finite element method for structural analysis.Int.J.Struct.Stab.Dyn,vol.13,1350007.
He,W.Y.;Ren,W.X.(2013b):Trigonometric wavelet-based method for elastic thin plate analysis.Appl.Math.Model,vol.37,pp.1607-1617.
Kushwaha,M.S.;Halevi,P.;Dobrzynsi,L.;Diafari-Rouhani,B.(1993):A-coustic band structure of periodic elastic composites.Phys.Rev.Lett.vol.71,pp.2022-2025.
Kushwaha,M.S.;Halevi,P.;M artinez,G.;Dobrzynski,L.;Djafari-Rouhani,B.(1994):Theory of acoustic band structure of periodic elastic composites.Phys.Rev.B,vol.49,pp.2313-2322.
Ko,J.;Kurdila,A.J.;Pilant,M.S.(1997):Triangular wavelet based finite elements via multivalued scaling equations.Comput.Meth.Appl.Mech.Eng,vol.146,pp.1-17.
Li,B.;Dong,H.B.(2012):Quantitative identification of multiple cracks in a rotor utilizing wavelet finite element method.CMES-Comput.Model.Eng.Sci.,vol.84,no.3,pp.205-228.
Li,B.;He,Z.J.(2013):A benchmark problem for comparison of vibration-based crack identification methods.CMES-Comput.Model.Eng.Sci.,vol.93,no.4,pp.293-316.
Li,B.;Chen,X.F.(2014):Wavelet-based numerical analysis:A review and classification.Finte Elem.Anal.Des,vol.81,pp.14-31.
M oiseyenko,R.P.;Laude,V.(2011):Material loss influence on the complex bnad structure and group velocity in phononic crystals.Phys.Rev.B,vol.83,064301.
M ead,D.J.(1973):A general theory of harmonic wave propagation in linear periodic systems with multiple coupling.J.Sound Vib,vol.27,pp.235-260.
Tanaka,Y.;Tamura,S.-I.(1998):Surface acoustic waves in two-dimensional periodic elastic structures.Phys.Rev.B,vol.58,no.12,pp.7958.
Tanaka,Y.;Tamura,S.(1999):Acoustic stop bands of surface and bulk modes in two-dimensional phononic lattices consisting of aluminum and a polymer.Phys.Rev.B,vol.60,pp.13294-13297.
Tarasenko,O.S.;Tarasenko,C.V.;Yurchenko,V.M.(2004):Localization of a transverse elastic wave in a sem i-bounded acoustic superlattice of ferromagnetic and superconducting layers:1.slip boundary.Acoust.Phys.,vol.50,no.5,pp.602-611.
Veres,I.A.;Berer,T.(2012):Complexity of band structures:sem i-analytical finite element analysis of one-dimensional surface phononic crystals.Phys.Rev.B,vol.86,104304.
W ilkinson,J.H.(1965):The Algebraic Eigenvalue Problem.Oxford:The Clarendon Press.
Xiang,J.W.;Chen,X.F.;He,Z.J.;Dong,H.B.(2007):The construction of 1D wavelet finite elements for structural analysis.Comput.Mech,vol.40,pp.325-339.
Xiang,J.W.;Chen,X.F.;He,Z.J.;Zhang,Y.H.(2008a):A new wavelet-based thin plate element using B-spline wavelet on the interval.Comput.Mech,vol.41,pp.243-255.
Xiang,J.W.;Chen,X.F.;Yang,L.F.;He,Z.J.(2008b):A class of waveletbased flat shell elements using B-spline wavelet on the interval and its applications.CMES-Comput.Model.Eng.Sci.,vol.23,pp.1-12.
Xiang,J.W.;Liang,M.(2011):Multiple damage detection method for beams based on multi-scale elements using Herm ite cubic spline wavelet.CMES-Comput.Model.Eng.Sci.,vol.73,pp.267-298.
Xiang,J.W.;M atsumoto,T.;Wang,Y.X.;Jiang,Z.S.(2011):A hybrid of interval wavelets and wavelet finite element model for damage detection in structures.CMES-Comput.Model.Eng.Sci.,vol.81,pp.269-294.
Xiang,J.W.;Wang,Y.X.;Jiang,Z.S.;Long,J.Q.;M a,G.(2012):Numerical simulation of plane crack using herm ite cubic spline wavelet.CMES-Comput.Model.Eng.Sci.,vol.88,pp.1-16.
Yang,Z.B.;Chen,X.F.;Li,B.;He,Z.J.;M iao,H.H.(2012):Vibration analysis of curved shell using B-spline wavelet on the interval(BSW I) finite elements method and general shell theory.CMES-Comput.Model.Eng.Sci.,vol.85,no.2,pp.129-155.
Yang,Z.B.;Chen,X.F.;Zhang,X.W.;He,Z.J.(2013):Free vibration and buckling analysis of plates using B-spline wavelet on the interval Mindlin element.Appl.Math.Model.,vol.37,no.5,pp.3449-3466.
Yang,Z.B.;Chen,X.F.;Li,X.;Jiang,Y.Y.;M iao,H.H.;He,Z.J.(2014):Wave motion analysis in arch structures via wavelet finite element method.J.Sound Vib.,vol.332,no.2,pp.446-469.
Yang,Z.B.;Chen,X.F.;He,Y.M.;He,Z.J.;Zhang,J.(2014):The analysis of curved beam using B-spline wavelet on interval finite element method.Shock Vib.,738162.
Zienkiew icz,O.C.;Taylor,R.L.;Zhu,J.Z.(2005):The Finite Element Method:Its Basis and Fundamentals(Sixth editon).Oxford:Butterworth-Heinemann.
 Computer Modeling In Engineering&Sciences2014年5期
Computer Modeling In Engineering&Sciences2014年5期
- Computer Modeling In Engineering&Sciences的其它文章
- Cauchy Problem for the Heat Equation in a Bounded Domain without Initial Value
- Flexural Wave Dispersion in Bi-material Com pound Solid and Hollow Circular Cylinders
- Numerical Solution for a Class of Linear System of Fractional Differential Equations by the Haar Wavelet Method and the Convergence Analysis
