基于遗传优化LMBP算法的变形分析与预报

曾凡祥，胡家赋，易 锋

(广州海洋地质调查局，广州 510760)

随着变形监测数据分析方法的发展，BP神经网络已用于大坝变形预报，其精度优于传统方法［1-5］。但标准的BP网络模型有很多缺点，主要是:ⓐ易收敛于局部极小点，这是个致命的缺点;ⓑ学习收敛速度太慢;ⓒ网络中间层的层数以及它的单元数选取无理论上的指导等。本文拟通过引入遗传算法与LM算法优化BP神经网络 (简称为GA-LMBP算法)，并对网络结构进行试算，以对标准的BP网络模型进行改进。

a.采用遗传算法对网络初始权值进行优化。遗传算法具有全局搜索性能［6］，可以很好地解决网络收敛于局部最小点这一问题。

b.采用LM算法优化BP神经网络 (简称LMBP算法)。就训练次数和准确度而言，LMBP算法明显优于标准的BP算法［7］，能有效改进标准BP网络模型学习收敛速度慢的缺点。

c.采用试算方法确定隐含层层数及节点数。

1 网络建立的步骤

网络建立的步骤如下:

a.网络结构的确定。对数据进行预处理;确定输入输出层节点数和隐含层节点数 (采用试算的方法)，即确定好网络模型的结构。

b.根据神经网络结构的参数，确定遗传算法的参数个数，随机产生一组种群，用遗传算法进行优化，得出一个较好的个体 (即网络的权值与阈值)，将这一个体进行解码，得出遗传优化后的网络权值、阈值。

c.建立LMBP算法对经遗传优化后的权重再次进行修正，得到修正后的网络模型。

d.利用训练好的模型，输入相应观测值，对变形位移进行预测。

2 网络结构的确定

2.1 输入输出节点的确定

大坝位移的计算方法为

式中 f(H)——水压分量;

f(T)——温度分量;

f(θ)——混凝土的渐变和基岩流变引起的时效分量。

从式 (1)提取出以下10个输入节点因子:

水压分量:H、H2、H3;

温度分量:T1、T2、T3、T4、T5、T6;

网络模型的输出节点则为大坝的变形量。

2.2 隐含层数及隐含层节点数的确定

对于神经元网络来讲，首先应该确定选用隐含层的层数。而具有一个隐含层的BP神经网络可以实现任意的n维到m维的映射。从网络结构的编程实现上考虑，要比增加更多的隐含层简单得多，其训练效果也比增加层数更容易观察和调整［1］。因此本文采用一个隐含层。

隐含层节点数的选择对网络的性能影响很大。对隐含层节点数的确定许多学者提出了许多不同的方法，但目前并没有一种科学的、普遍的理论与方法。本文将通过对不同神经元数进行训练，对比计算结果得出最优节点数。即通过试算法确定隐含层节点数，这种方法更具有可靠性及可操作性。

本文选择不同的隐含层节点进行训练。训练结果表明:当隐含层节点数为18时，网络收敛最快，具有较高的预测精度。因此，学习样本采用11-18-1的网络结构形式。

这里的激活函数采用S型激活函数:

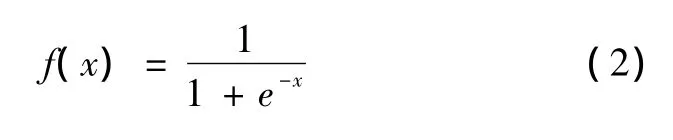
为提高训练速度和灵敏性、有效避开Sigmoid函数的饱和区，要求数据输入值在0～1之间。因此，需对输入数据进行归一化处理。由于输出层节点也采用Sigmoid转换函数，输出变量也必须进行相应的预处理。

样本数据的归一化处理公式为

样本的还原处理为

上二式中 X'——归一化后的数据;

Xmin——每一个样本模式下输入值或目标值的最小值;

Xmax——每一个样本模式下输入值或目标值的最大值。

3 遗传优化网络初始权重

对于随机产生的网络初始权重，如果不使用遗传算法，则由神经网络模型直接进行权重的修正，而这样网络易收敛于局部最小点。本文将采用遗传算法对网络初始权重进行修正。

3.1 染色体的表达与初始种群的生成

按神经网络生成初始权重的常规方法来生成网络的权重，由于完整的网络权重Q为

对于本文所使用的11-18-1网络，设定输入层节点数R=11，隐含层节点数S1=18，输出层节点数S2=1。则网络的权值数目为

由于本文使用的是浮点数编码，因此一个染色体为1×235的实数矩阵。设定种群长度为100，即需在初始化时产生含100个染色体的初始种群。且染色体的表达和网络权重一一对应，染色体可以转换成权重。

3.2 目标函数与适应度函数

用遗传算法优化网络权重的目的是得到一组较好的权重，使得网络误差平方和最小，因此定义目标函数为:这里的M是一个较大的系数，是为了保证适应度函数的函数值不至于太小，取M=100。

由于遗传算法只能朝着适应函数值增大的方向进化，因此，适应度函数可以构成目标函数倒数的形式:

3.3 进化运算

选择运算是逐代更新的过程，它的特性决定了种群的进化趋势。而选择概率是描述进化运算性能的一个很重要的因素。本文采用排序法确定染色体的选择概率。

排序法的运算规则为:忽略实际染色体的适应值，用染色体的顺序计算出相应选择概率，计算原则为小适应值对应低选择概率、大适应值对应高选择概率。这种方法能保证大适应值染色体获得高的选择概率，防止某些超级染色体过快地把持遗传过程。本文设定选择算子的初始选择概率为0.07，并在程序运行中不断调整。

3.4 遗传运算

种群中序号为1的染色体是上一代中适应值最大的染色体，为了防止最佳染色体的退化，设定该染色体不参与交叉和变异的遗传操作。因此，父代染色体从序号为2～N的种群范围内产生。文中交叉算子采用算术交叉的形式，初始的交叉概率设为0.9、变异概率设为0.1，在遗传运算过程中，对交叉概率与变异概率进行适当的调整。

4 LMBP算法训练网络

经过遗传运算后，已得到一个较好的权重。以这个权重作为初始权重，使用LMBP算法进行修正。

4.1 网络的顺传播

首先根据网络结构与初始权重矩阵，逐个输入变量观测数据，计算每个样本的输出误差，采用的符号定义如下:

输入向量:X= ［α1、α2、…、αR］T;

期望输出向量:y;

中间层各单元输入激活值向量:NET=［net1、net2、…、netS1］T;

中间层各单元输出变量:O= ［o1、o2、…、oS2］T;

输出层至隐含层的连接权 W1ij(i=1，2，…，S1;j=1，2，…，R);

隐含层至输出层的连接权 W1ij(i=1，2，…，S1;j=1，2，…，S1);

为方便编程计算，将中间层阈值的转置加到W1权重矩阵的最后一行上，则W1变为了S1×R矩阵;将输出层各单元阈值进行转置，然后加至W2权重矩阵的最后一行上，则W2变为了S2×S1矩阵;X添加一个为－1的行向量，加到最后一行;O的最后一行添加一个－1的元素。

激活函数为

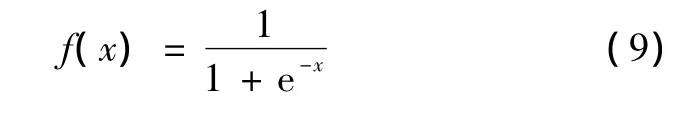
a.用矩阵X、连接权重矩阵W1计算隐含层各神经元的输入值(激活值NET)与隐含层各单元的输出向量Ok:

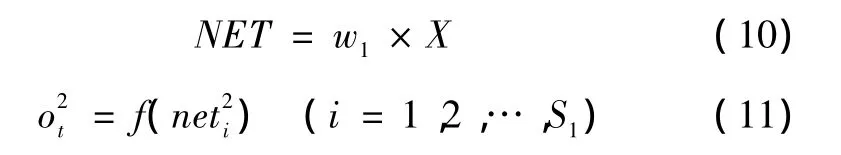
b.用中间层的输出O、连接权重矩阵W2计算输出层单元的输入向量L、实际输出

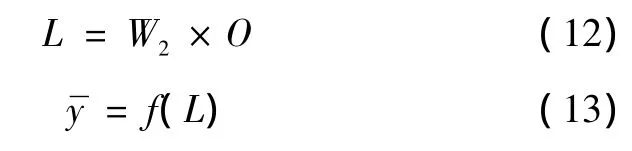
c.计算各输入样本的误差Eq及误差信号项、误差对权的偏导数:

然后计算出各权值元素的偏导数，并将所有的值填入Jacobian矩阵中。不断地计算式 (1)～式(3)，直到所有的样本数据输入完毕。

4.2 输出误差的逆传播

根据式 (15)即可求出权重矩阵的校正量，不断地迭代，直到迭代次数超限或者误差平方满足要求。

5 大坝变形分析与预报

选取某大坝历史观测资料进行分析与预报，采用1999～2001年150期次的径向位移、水位、气温和时效的实测资料作为初始训练样本建立神经网络模型，采用遗传算法训练各层的连接权值和阈值，并采用LMBP算法进行修正并保存。然后利用训练好的网络预报2001～2003年80个期次的变形位移值。为了验证GA-LMBP模型的适用性，本文建立了GA-LMBP模型、LMBP模型和标准BP算法模型 (简称:SBP模型)，对这三个模型的拟合、预报结果进行比较分析。

5.1 预测精度分析

为比较遗传优化后的LMBP神经网络模型 (简称GA-LMBP)的优劣，分别对GA-LMBP模型、LMBP模型、标准BP模型进行比较分析，比较预测精度及其运算性能。为便于比较，三种模型的目标误差值均设为0.001。对各模型进行多次运算，GA-LMBP模型预测误差见图1，各模型多期预测值所计算的均方误差见表1、图2。

图1 GA-LMBP模型L7H291测点实测值与预报值对比

表1 各模型预测值均方误差比较

图2 各模型预测值均方误差比较

为更清楚地比较GA-LMBP模型与其他模型的预测精度，用各模型分别运算5次，求出平均相对误差和绝对误差，结果见表2。

表2 L7H291测点平均相对误差与平均绝对误差

从GA-LMBP模型的实测值与预测值的预测误差可以看出，预测值与实测值接近，具有较高的精度与较强的稳定性。

由表1、表2可以看出，三种模型中，GA-LMBP模型、LMBP模型、SBP模型的大坝变形预测精度均较高。可以看出，在相同误差指标下，无论从平均相对误差、平均绝对误差还是均方误差的平均值考虑，GA-LMBP模型均优于LMBP模型与标准的BP模型。这说明了BP模型采用LM算法后精度有所提高，而采用遗传神经网络进行BP神经网络的权重优化后，预测值具有更高的精度。

5.2 模型性能比较分析

因遗传神经网络仅用于初始权重的选择与优化，运算量小，所耗费的资源小。本文仅比较LMBP模型与标准BP模型的运算时间及其训练所需的步数。表3中的数据均是模型分别运行5次后所得的平均值。

表3 L7H291测点的各模型训练时间与训练步数的比较

由表2可以看出，在相同误差指标下，LMBP模型比标准的BP网络具有更快的收敛速度，仅需少量的训练步数即可收敛。而遗传优化的LMBP神经网络运算时间与LMBP相当，且优化后的网络权重可更快得收敛，训练步数亦可减少，即遗传优化的LMBP神经网络也拥有较快的运算速度。

5.3 训练样本数量对精度的影响

为考察拟合数据序列的长短 (或训练样本的数量)对预报精度的影响，分别选取不同时段观测数据，建立 GA-LMBP模型。然后，利用对2001年9月～2003年5月间的环境量数据对水平位移观测值进行预报。预报结果见表4。

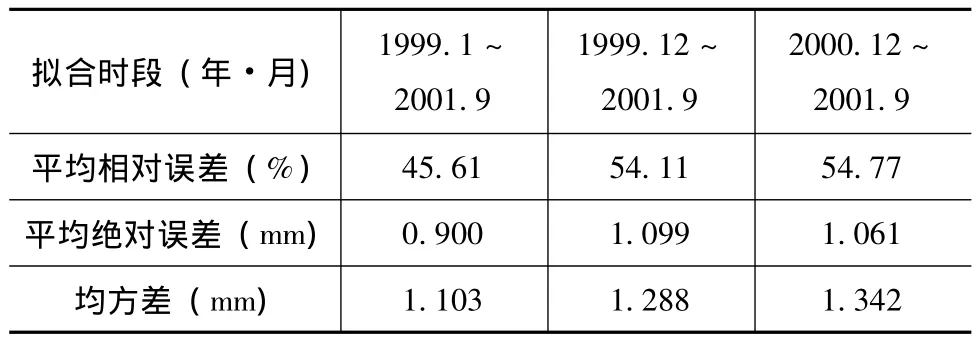
表4 L7H291测点不同拟合时段下的预测精度对比

由表2可以看出，拟合数据序列越长，GA-LMBP模型的预报精度越高。说明随着训练样本的增加，网络的“学习”能力在不断增强。

6 结语

为解决BP算法收敛速度慢、计算量大的问题，本文引入LMBP算法代替标准的BP神经网络，为进一步提高神经网络预测的精度及利用遗传算法的全局搜索能力，引入遗传算法进行神经网络初始权重的选取，并通过编程建立了GA-LMBP大坝变形位移预测模型并进行预测。

实验结果表明:aGA-LMBP模型具有很高的预测精度，预测精度高于LMBP模型，比传统的BP模型高得多;b如样本足够多，GA-LMBP模型可获得更高的预测精度;cGA-LMBP模型具有较快的收敛速度，能大大减小网络的计算量，极大地提高网络的学习效率，适用于大坝监测的实时预报。

［1］吴秀娟．人工神经网络在大坝监测数据分析中的应用研究［D］．武汉:武汉大学，2003．

［2］杨杰，吴中如，顾冲时．大坝变形监测的BP网络模型与预报研究［J］．西安理工大学学报，2001，17(1):25-29．

［3］黎昵，岳建平，段鹏．改进模糊神经网络模型及其在大坝监测中的应用［J］．水电自动化与大坝监测，2007，31(1):74-76．

［4］吴云方，李珍照．改进的BP神经网络模型在大坝安全监测预报中的应用［J］．水电站设计，2002，18(2):21-24．

［5］田斌，徐卫超，何新基．前馈神经网络法在大坝安全监控中的应用［J］．水利发电，2003，29(7):60-63．

［6］张栋，蔡开元．基于遗传神经网络两阶段学习方案［J］．系统仿真学报，2003，15(8):1088-1090．

［7］李炯城，黄汉雄．神经网络中LMBP算法收敛速度改进的研究［J］．计算机工程与应用，2006，42(16):46-49．