VPRS和LSSVM的联合建模对于金属粉末性能的测定

王 莉 周新东

（1.湖南商学院 计算机与电子工程学院，湖南 长沙 410205；2.湖南长远锂科有限公司，湖南 长沙 410205）

0 引言

雾化合金粉末是当今粉末冶金领域中品种最多、产量最大、应用最广的合金粉，在制造高温合金材料、磁性材料和热喷涂层上都有广泛应用，合金粉末的质量直接影响到后续产品的质量和二次开发。但是在实际制粉生产过程中产生了大量的数据，这些数据中有的非常重要却往往被忽视或者无法记录，还有一些指标无法预测和控制，因此获取的信息非常不完整，提供给现场的信息也非常有限，甚至不准确。如何从大量数据中获取有用的知识，以帮助决策者及时发现问题、分析问题和解决问题，提高生产管理的科学性和先进性，优化制粉工艺和生产，成为迫在眉睫的问题。

粗糙集理论(Rough Set)不仅能够找出与类别密切相关的不可约简属性集合，而且还使用上下近似对样本所属类别的确定程度进行刻画[1]，它能充分考虑数据的不精确、不确定性，符合人类对事物的认识程度，可与神经网络、支持向量机、模糊系统等数据挖掘方法相结合[4-10]，用于提高挖掘模型的泛化、学习能力以及处理不确定性的能力。

支持向量机（SVM）是建立在统计学习理论基础上的一种新型的机器学习方法[2-3,11-16]，由于具有良好的泛化能力，目前已经在许多领域得到了成功的应用。它是对结构风险最小化的近似，较好地解决了小样本、非线性、高维数、局部极小等问题。最小二乘支持向量机(LS_SVM)是SVM的一种改进算法，它是SVM在二次损失函数下的一种形式，用二次损失函数取代SVM中的不敏感损失函数，通过构造损失函数将原SVM中算法的二次寻优变为求解线性方程，降低了计算的复杂性。国内已有不少文献对粗糙集和SVM的联合建模进行了阐述，现在已运用于材料[4,16]、中医药[5]、故障诊断[6]、冶金工业[8]等。

本文引入基于集对容差关系的变精度粗糙集算法，利用阈值α，使得允许一定程度上错误分类的存在，通过对α的调节和控制，提高容差类划分的准确性和灵活性。同时运用贪心算法进行属性约简，最后结合LS_SVM对制粉工业的不完备信息系统进行建模，提高模型的预测精度和泛化能力。

1 基于集对容差关系的VPRS理论

定义1：设不完备信息系统S＝(U,AT,V,f)，其中U是一个对象的非空有限集合，AT是非空有限的属性集合；对于∀a∈AT，有a∶U→Va，其中Va是属性a的值域。属性值域集合V=∪a∈ATVa；f为信息函数，对于∀a∈AT,∀x∈U，有 f(x,a)∈Va。

定义2：设(U,A)是一个不完备信息系统，其中U是对象集，A是属性集，∀x,y∈U，B⊆A，0.5≤α≤1，定义集对势容差关系为：

这里，a、b、c分别是X和Y的同一度、差异度和对立度；uB(x,y)称为X和Y的联系度；Ix={(x,x)｜x∈U}是U上的恒等关系。由文献[5]可知，由同一趋势的无穷大势所满足的条件可推出同一度阈值0.5≤α≤1。

2 LS_SVM模型

设样本集为S=[(xi,yi)](i=1,2,…l)，xi为输入矢量，yi为目标输出矢量，l为样本数。根据支持向量机建模原理，构造最优线性决策函数：

式中，ξ为误差，c＞0为惩罚系数，c越大表示对超出误差的样本的惩罚越大。这个优化问题的解由如下的Lagrange函数的鞍点给出：

其中 αi＞0 为 Lagrange 系数。 求 L(ω,b,ξ,α)对 ω，b，ξ，αi的偏导数，并令其等于零，消除变量ω和ξ，得到线性方程为：

式中，Y=[y1,y2,…yl]T，I=[1,1,…1]T，α=[α1,α2,…αl]，Ω=φ(xi)Tφ(xj)=K(xi,xj)，为核函数。求出αi和b，并代入式（9）中，得到预测模型为：

3 基于VPRS和LS_SVM的预测模型的建立

3.1 属性约简与知识获取

属性约简的主要目的是为了解决高维数据计算的复杂性和准确性问题，消除冗余和不相关属性对计算过程和最终结果造成的影响。其方法有很多，如PCA主成分分析法、启发式约简算法、基于可辨识矩阵的约简算法、基于遗传算法的约简算法等。文献[5]中提到，可辨识矩阵约简算法的时间复杂度和空间复杂度比较高，一般不适合在实际工程中应用。而PCA主成分分析是把高维空间的问题转换到低维空间来处理，但是该算法对极端值及缺失值非常地敏感，而极端值与缺失数据会带来残缺或错误的分析结果。本文采用一种启发式约简算法，即贪心算法，将各属性按照重要性从大到小加入到约简属性集中，直到满足约简条件为止。

定义3：设S=(U,A)是一个不完备信息系统，其中A=C∪D,C∩D=φ，C为条件属性，D为决策属性。属性子集P⊆A，定义属性集P的不可区分关系IND(P)为：用U/IND(P)表示U中的一个划分，简记为U/P。

定义4：属性子集P⊆C，属性P相对于D的β的近似依赖度定义为：

定义5：RED(C,D,β)是条件属性C相对于决策属性D的β近似约简，有 RED(C,D,β)⊆C，且满足：（1）γ(P,D,β)=γ(RED(C,D,β),D,β)；（2）去掉RED(C,D,β)中的任意一个属性都会使（1）不成立。

3.2 LS_SVM参数辨识与优化

高斯核函数由于存在局部性，因此核函数学习能力很强，但是泛化性能较弱，而多项核函数是一种全局核函数，泛化性能强，因此考虑把这两类核函数混合起来应用于LS_SVM算法中。混合核函数的表达式为：

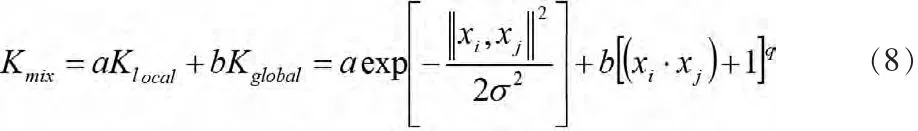
式中，a和b是决定两者组合比例的系数，有0≤a,b≤1，且a+b=1。

3.3 基于VPRS和LS_SVM的预测模型的框图

图1 基于VPRS和LS_SVM的建模示意图Fig.1 Structure of the model based on VPRS and LS_SVM

4 系统实现

4.1 样本数据的VPRS处理

为检验预测模型的有效性和优越性，本文以某镍基水雾化合金粉末生产过程为例进行仿真测试。过程工艺参数由熔液的出料温度(a1)、熔液液流直径(a2)、熔液雾化速度(a3)、高压水压(a4)、熔液流量(a5)表示，镍基合金粉末指标由流动性(d1)、压缩性(d2)、松装密度(d3)表示。取20组数据作为模型输入样本，其初始决策表如表1所示。

表1 初始决策表Tab.1 Initial decision table

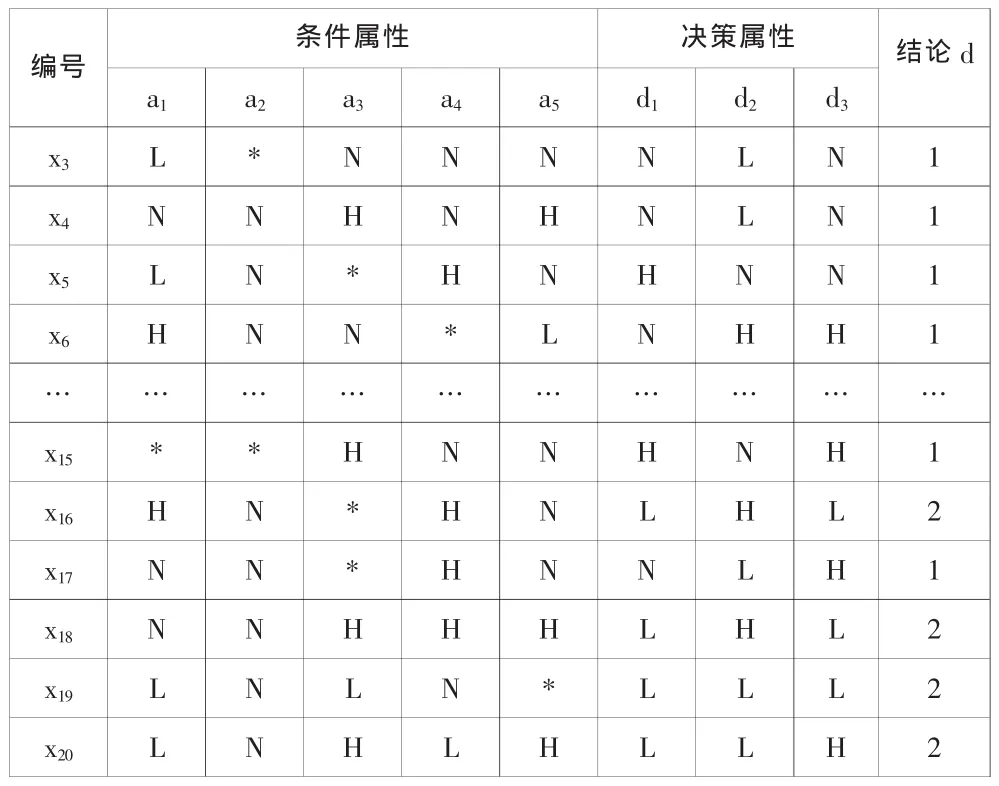
表中，属性有三种特征值，分别为：低（L）、正常（N）、高（H）。

运用贪心算法对初始决策表进行约简，最终获得属性约简结果{a1，a3，a4}，把该结果作为LS-SVM的输入进行训练和分类，可以看出输入量由原来8个变为3个，大大降低了训练模型的复杂度。

4.2 LS_SVM预测模型

选择松装密度(d3)为预测对象，设定LS_SVM的混合核函数的各项参数为：a取0.9左右，b取0.06，高斯核半径σ取1.44，惩罚系数C取160，多项式核函数q取1，选定40个点，预测值和相对误差曲线如图2所示。经计算，预测的最大相对误差为1.40%，平均相对误差为0.92%，这表明所建立的模型具有很好的预测能力和泛化能力，它能够根据过程工艺参数有效预测松装密度，可以满足实际应用的要求。

4.3 实验结果的分析与比较

为了评价VPRS+LS_SVM模型，用同样的数据对基于人工神经网络（BPNN）的LS_SVM进行建模、训练和测试，结果如图 3。从以上两图可以看出，VPRS+LS_SVM的预测性能明显优于BPNN+LS_SVM方法。

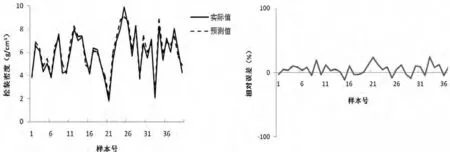
图2 VPRS+LS_SVM仿真结果Fig.2 VPRS+LS_SVM simulation results

图3 BPNN+LS_SVM仿真结果Fig.3 BPNN+LS_SVM simulation results

为进一步评价两种方法的性能，对镍基合金粉末的流动性和压缩性进行了预测，结果如表2所示。表中采用最大相对误差（Emax）和相对均方根误差（RMSE）作为评价指标。

式中，yi和分别是第i个样本的实际值和预测值。

表2 两种LS_SVM核算法预测性能比较Tab.2 Forecast performance comparison of two kernel algorithms

由表2可以看出，对镍基合金粉末的流动性和压缩性进行VPRS+LS_SVM和BPNN+LS_SVM两种算法比较后，前者算法的相对误差和均方根误差都比后者的要小，同样说明了VPRS+LS_SVM模型的较好的预测性能。

5 结论

针对制粉生产过程参数和指标的不完整性和不确定性，本文提出了基于VPRS和LS_SVM的预测模型的建模方法，该模型首先通过VPRS属性分类和贪心算法的属性约简构造出精简的训练样本集，然后将其样本集输入LS_SVM模型中用于训练，实现关键参数的实时预测。

将建立的模型用于镍基合金粉末生产过程的返料组份预测，结果表明该模型消除了不相关变量的干扰，提高了训练的泛化能力，具有预测精度高、实时性好等优点，在制粉工艺优化和控制领域有巨大的应用潜力。

［1］王文辉,周东华.基于遗传算法的一种粗糙集知识约简算法[J].系统仿真学报,2001,13(8):91-96.

［2］王雪松,田西兰,程玉虎,易建强.基于协同最小二乘支持向量机的Q学习[J].自动化学报,2009,35(2):214-219.

［3］梁伟锋,汪晓东,梁萍儿.基于最小二乘支持向量机的压力传感器温度补偿[J].仪器仪表学报,2007,28(12):2235-2238.

［4］蔡从中,温玉锋,朱星键,等.基于工艺参数的7005铝合金力学性能的支持向量回归预测[J].中国有色金属学报,2010,20(2):323-328.

［5］颜志国.基于粗糙集和支持向量机的表面肌电特征约简和分类研究[D].上海:上海交通大学,2008.

［6］曾志强.支持向量分类机的训练与简化算法研究[D].杭州:浙江大学,2007.

［7］蒋少华,桂卫华,等.基于RS与LS-SVM多分类法的故障诊断方法及其应用[J].中南大学学报:自然科学版,2009,40(2):447-451.

［8］王新华,桂卫华,王雅琳,等.混合核函数支持向量机的磨矿粒度预测模型[J].计算机工程与应用,2010,46(12):207-209.

［9］段丹青,陈松乔,杨卫平,王加阳.使用粗糙集和支持向量机检测入侵[J].小型微型计算机系统,2008,29(4):627-630.

［10］王泳,胡包钢.应用统计方法综合评估核函数分类能力的研究[J].计算机学报,2008,31(6):942-952.

［11］Cristianini N,Shawe-Taylor J.支持向量机导论[M].李国正,王猛,增华军,译.北京:电子工业出版社,2005.

［12］Cortes C,Vapnic V.Support vector networks[J].Machine Learning,1995,20(1):1-25.

［13］Burges C J C.A tutorial on support vector machines for pattern recognition[J].Data Mining and Knowledge Discovery,1998,2(2):1-48.

［14］Vapnik V.Statistical learning theory[M].New York:Willey,1998.

［15］YUAN Sheng-fa,CHU Fu-lei.Support vector machines-based fault diagnosis for turbo-pump rotor[J].Mechanical Systems and Signal Processing,2006,20(4):939-952.

［16］JIANG Shao-hua,GUI Wei-hua,YANG Chun-hua,et al.Fault diagnosis of lead-zinc smelting furnace based on multi-class support vector machines[C]//Proceedings of the Sixth IEEE International Conference on Control and Automation.Guangzhou,2007:1643-1648.