桥梁式高架车站的固有频率及振型分析

孙 艳，李俊杰

（武汉科技大学，武汉 430065）

随着我国城市化建设步伐的加快，交通拥堵、环境污染、人口密集、土地资源匮乏等诸多城市问题日益明显，而城市交通问题是较为突出的一个，所以近年来我国城市轨道交通建设速度加快，各大城市也都提出了符合自身实际的城市轨道交通线网规划和近期建设规划［1］，各类新型的高架车站也应运而生。高架车站顾名思义就是列车行驶在地面以上的高架结构上，常见的高架车站类型主要有三种：桥梁结构式车站、空间框架式车站、桥建分离式车站。

桥梁结构式车站作为“建桥合一”结构中的一种新型车站，已逐步成为当今城市轨道交通高架车站的主流车站形式，尽管它实质上仍然是桥梁结构，但它兼具了建筑与桥梁的功能，是由一般桥梁结构延伸和拓展而来。大多数的高架桥穿梭于闹市区和居民区，振动的产生都会对周边的环境带来不利的影响，例如：人处于振动环境中，将会引起人体生理和心理的效应，例如感到不舒服、麻感、头晕、困倦，严重时出现出汗、头痛、心慌甚至损害到人体心脏。当振动频率为5Hz时，振动加速度达到0.1g时人就感到不舒服，达到0.4g时人就觉得不可忍受了［2］。因此，如何减小结构系统的振动影响具有十分重要的现实意义。

1 工程背景

以重庆轨道交通2号线某轻轨高架车站为背景，车站具有往返双向车道，采用“T”型独柱桥墩，站台、轨道箱型梁、盆式橡胶支座等依次直接支撑在T型桥墩盖梁上。车站全长63m，宽为18m，机车轨道位于车站中间，站台分布于桥梁两侧，纵向设置一条伸缩缝；桥墩采用C40混凝土，间距10m，厚度3m，高度10m，所研究分析的车站范围内共设有7个桥墩；站台采用C30混凝土，高度1.5m，宽度5.1m，站台板厚200mm，双侧布置；轨道梁采用连续钢筋混凝土箱型梁，混凝土材料等级C40，截面形式为单箱单室，梁高2.53m，顶板宽度即为车站宽度，底板宽为7.8m；钢轨采用60kg/m的重型钢轨，截面面积77.45cm2，截面惯性矩Iz＝3 217cm4、Iy＝524cm4；道床采用浮置板式轨道结构（两侧和底部均设有橡胶支座），底部设中心水沟，浮置板承轨槽内侧预埋PVC泄水管，钢轨内置，两侧和底部的橡胶垫可以在横向与纵向提供足够的弹性，可以达到较好的减振效果。

2 模型的简化

高架车站模型从上到下依次由站台、钢轨、连接钢轨与轨下垫板的扣件、轨下垫板、浮置板式道床、橡胶垫、轨道梁、盆式橡胶支座、桥墩等几部分组成，若要对各部分构件详细准确地建立单元、定义单元参数及类型，将会十分复杂，难以实现，因而需要对整个结构分析模型进行一定程度的简化与假设。建筑物的振动首先是由机车轮压作用在钢轨上，再由钢轨通过扣件、轨下垫板传到浮置板式道床，继而传到建筑结构上的。因此首先把钢轨当作振源，将扣件、轨下垫板、浮置板式道床作为一个整体来考虑，在建模过程中用六面体方块来模拟这个整体，按照0.65m的固定间距沿着车站纵向方向平行布置在桥面路基上，并采用弹簧连接的方式把钢轨和桥梁结构连接起来；箱型梁与桥墩之间的盆式橡胶支座同样采用弹簧连接的方式，更能接近实际情况，可以很好地体现出盆式橡胶支座在实际工程中的良好减振效果；将不考虑桥墩基础的影响，独柱桥墩与地面采用固结的连接方式。

3 有限单元模型及网格划分

以大型有限元软件ANSYS14.0为分析平台，建立研究分析模型，采用软件提供的PCG Lanczos法对所建模型进行模态分析。

3.1 模态分析原理

结构模态是结构振动的一种表征特性，分析结构的振动参数，如固有频率及振型，以用于控制外加动荷载频率或改变结构固有频率，以避免共振现象的出现。它也是模态叠加分析方法的基础［3］。

3.2 结构模型中所选用的单元类型

钢轨采用三维梁单元BEAM188进行模拟，能够很好的反映钢轨在实际使用过程中的各种变形；箱型梁、独柱桥墩以SOLID187单元来模拟，可以准确地反映箱梁整体性能好、结构变形小的特点；车站上部两侧的站台结构采用SHELL181单元来模拟，它不仅有较好的弯曲能力，同时还具有良好的膜力；箱型梁与桥墩之间的盆式橡胶支座以及浮置板式道床中钢筋混凝土支承块下的大橡胶垫板采用弹簧单元COMBIN14来模拟。由于自振频率ωd与阻尼比ξ存在关系式，而实际上ξ都很小，一般为0.01～0.1，则，所以结构可按无阻尼系统进行模态分析［4］。

3.3 结构模型的计算参数

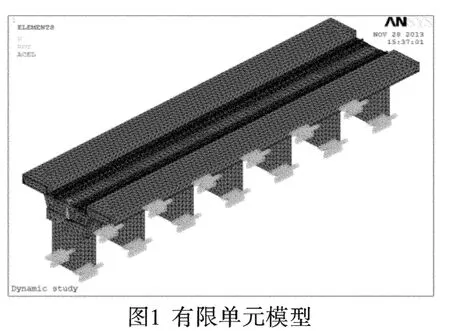
钢轨的弹性模量为2.1×1011N/m2，泊松比0.3，密度7 850kg/m3；站台板厚200mm，弹性模量取3.2×1010N/m2，泊松比0.2，设计密度2 500kg/m3；桥体箱型梁弹性模量为3.4×1010N/m2，泊松比0.2，设计密度2 500kg/m3，顶板宽度18m，底板宽度7.8m，梁高2.53m；桥墩弹性模量取3.4×1010N/m2，泊松比0.2，设计密度2 500kg/m3，高度10m；桥墩与箱梁连接处的盆式橡胶支座垂直刚度（弹簧系数）为1.0×1010N/m；钢轨与桥面路基之间的整体轨道系统垂直刚度为8.0×108N/m；双向往返车道的轨道间距为5m，扣件间距取0.65m。执行网格划分后且模态分析前的有限单元模型如图1所示。

4 结构的固有频率及振型

由于结构的前几阶固有频率对结构的振动影响最大，且发生的可能性更高。因此，提取前十阶固有频率及其对应的振型。

4.1 固有频率

固有频率是结构的固有属性，见表1。

表1 固有频率表

4.2 振型位移图

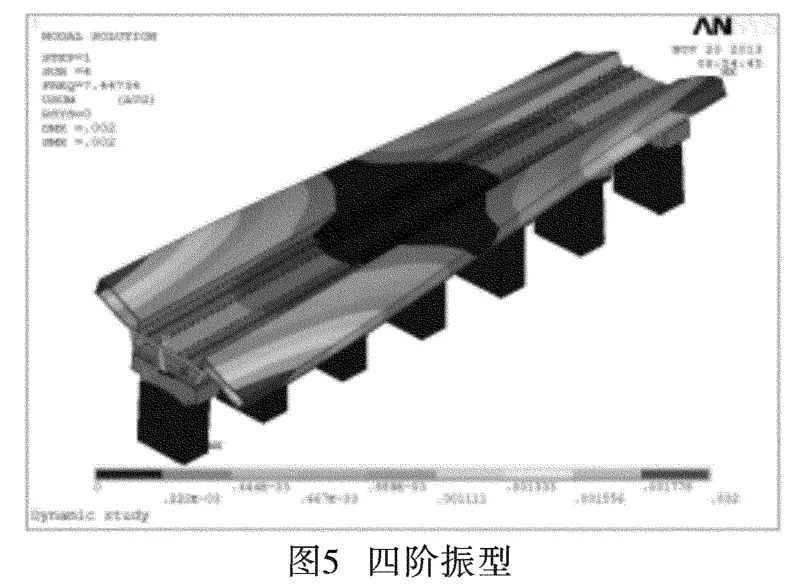
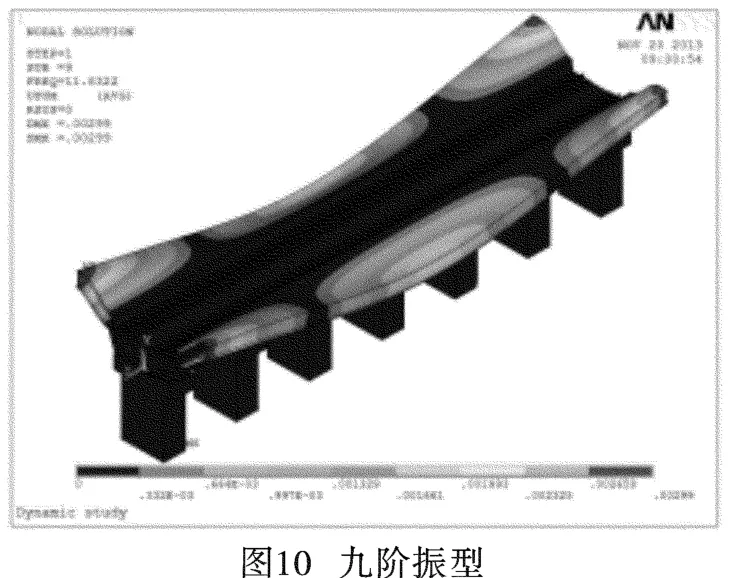
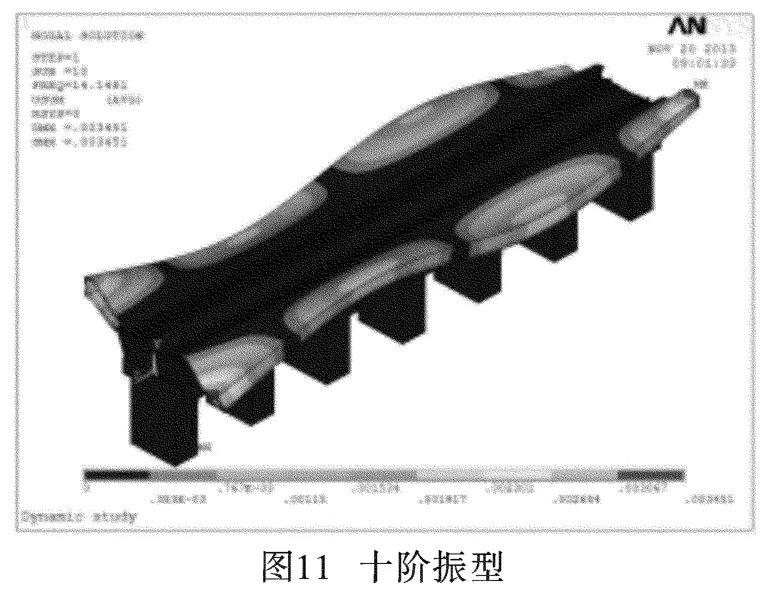
图2～图11分别为前十阶振型位移图。

从结构的振动位移图可以看到，随着产生位移的能量越来越大，整个结构系统由简单的整体侧移、平移逐渐演变成桥体上部结构的明显波动变形：一阶振型图表现为结构整体向Z轴正方向（水平方向）侧移；第二、三、六阶的振型图主要表现为结构上部两侧的站台在竖直方向上的上下摆动；第四、五、七、八、九、十阶的振型位移图则主要表现为上部两侧站台连续板沿着水平方向上的连续波动。结构单元节点的位移及挠曲度随着阶数的递增而逐渐增大，结构的最大位移发生在站台外侧边角部。

4.3 钢轨扣件间距对固有频率的影响

根据高速铁路设计规范的建议，分别选取了扣件间距为0.55m、0.6m、0.65m、0.7m［5］、0.725m［6］这5种工况进行比较，分析结果表明，当扣件间距为0.60～0.65m时，结构有更多的低阶固有频率值接近于5Hz，更能满足乘客的舒适性要求；当扣件间距为0.65m时，节点的最大振动位移值是最小的。因此，根据以上结论并结合钢轨安全性和工程成本的经济性，选定0.65m为最佳扣件节点间距。

5 结 语

模态分析作为一种用来确定结构振动特性的技术，通过它可以得到固有频率、振型和振型参与系数，其中固有频率和振型是承受动态载荷结构设计中的重要参数，也是动力学分析的出发点。

通过有限元软件ANSYS对桥梁结构式车站的固有频率及振型进行了研究分析，探讨出不同扣件间距对结构固有频率及振型的影响，找出最佳间距值，在一定程度上起到了有效的减振作用，更能满足乘客的舒适性和结构的安全稳定性要求。通过此类高架车站的成功建设与运营经验，并结合建模过程中的各项计算参数，可以通过选择合适的钢轨弹性模量、轨下垫层刚度与阻尼、支承块质量、桥墩盆式橡胶支座刚度等构件来达到良好的减振效果。

［1］ 张庆贺，朱合华，庄荣.地铁与轻轨［M］.北京：人民交通出版社，2002.

［2］ 练松良，王午生.轨道工程［M］.上海：同济大学出版社，2006.

［3］ 彭细荣，杨庆生，孙卓.有限单元法及其应用［M］.北京：清华大学出版社，2012.

［4］ 耿传智，田苗盛，董国宪.浮置板轨道结构的振动频率分析［J］.城市轨道交通研究，2007（1）：23.

［5］ 邱金帅，蔡小培，安彦坤.扣件间距对无砟轨道动态轨距的影响［J］.铁道建筑，2011（8）：106－108.

［6］ 李志红.城际轨道交通桥梁梁端扣件节点间距研究［J］.铁道工程学报，2009（8）：64－67.