复杂传动系统的故障特征提取分析的综合方法研究

段守泽 DUAN Shou-ze；徐玉秀 XU Yu-xiu；邢钢 XING Gang；杨文平 YANG Wen-ping

（①天津工业大学机械工程学院，天津300387；②天津市现代机电装备技术重点实验室，天津 300387；③天津职业技术师范大学，天津 300222）

（① School of Mechanical Engineering，Tianjin Polytechnic University，Tianjin 300387，China；②Tianjin Key Laboratory of Advanced Mechatronics Equipment Technology，Tianjin 300387，China；③Tianjin University of Technology and Education，Tianjin 300222，China）

0 引言

风力发电机组齿轮传动系统是整个风电机组的核心部件，其主要功用是将风轮在风力作用下所产生的动力传递给发电机并使其得到相应的转速[1]。如果齿轮传动系统出现故障，将会影响整个风电机组的运转，甚至造成停机[2]。由齿轮传动系统故障所造成的停机时间最长，造成的损失最大[3]。因此，对风电机组齿轮传动系统的故障状态进行分析并建立合理的故障识别方法就显得尤为重要。面对风电机组齿轮传动系统故障的频繁发生以及造成的巨额损失，唐新安等[3]借助时域信号的统计指标实现对齿轮箱故障的初步诊断，之后借助传统的快速傅里叶变换（Fast Fourier Transform，FFT）和功率谱对诊断结果进一步加以确认。HUANG等[4]研究了小波神经网络在风力机齿轮箱故障诊断中的应用。该方法借助小波变换的时频分析特性和神经网络的自学习功能，将小波函数作为神经网络的隐含层，提高了诊断精度，减少了神经网络的层数，加快了收敛速度。BARSZCZ等[5]提出了利用谱峭度诊断行星齿轮箱故障的方法。利用谱峭度对冲击信号敏感特性检测出信号中的冲击成分，从而诊断出故障原因。INALPOLAT等[6]对行星齿轮箱的建模和动力学行为进行了研究，为其复合传动引起的故障相互调制和耦合等故障机理提供了依据。

综上所述，现有对齿轮故障机理的研究主要为一对啮合齿轮或结构较简单的传动系统的单一故障。对于三级传动的复杂齿轮传动系统，其振动机理复杂，产生的复杂故障不能简单的用单一的故障机理诊断其故障类型。为此，本文在研究1.5MW风力发电机组齿轮传动系统的故障时，采用实验分析与模拟分析相结合的方法对其故障状态做出准确的分析与诊断。并用振动响应信号功率谱的关联维数作为齿轮传动系统的故障特征量，成为复杂故障诊断的一种方法。

1 对实验信号的处理分析

对某风力发电场的1.5MW风电机组齿轮传动系统进行振动信号采集，采用LDS PHOTONⅡ型便携式4通道采集仪，PCB单向加速度传感器，测点在齿轮箱后盖靠近输出轴处，如图1所示。对采集到的加速度振动信号，用MATLAB绘制其径向信号的功率谱如图2所示。

图1 信号采集点位置示意图

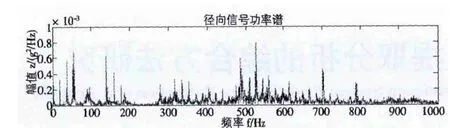
图2 实验信号的功率谱

针对输出轴附近振动大、故障不能确定的情况，对高速级啮合频率488Hz附近频带做细化谱，细化抽选比20，细化中心频率489Hz，细化谱点数1024。具体如图3所示。

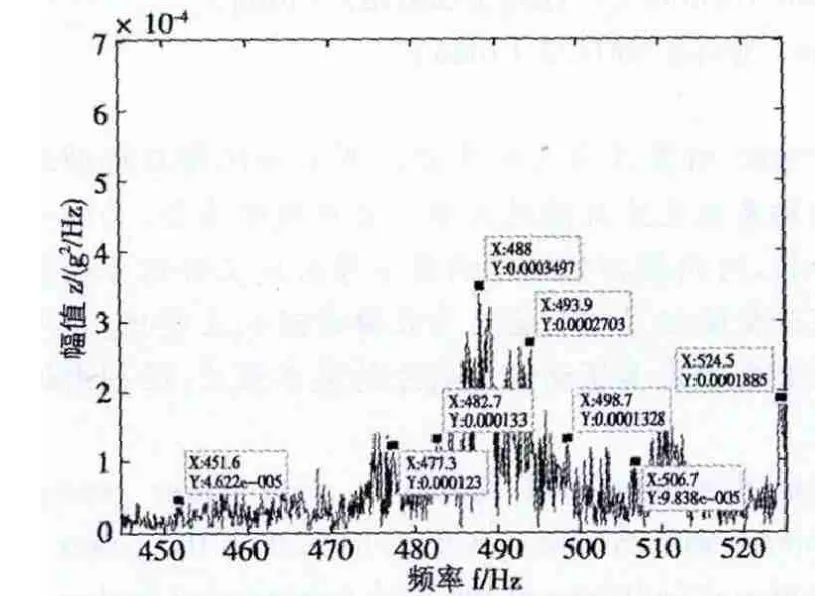
图3 高速级啮合频率处细化谱

从图3可知，高速级啮合频率为488Hz，附近有5.3Hz、5.9Hz，18.1Hz、18.7Hz，10.7Hz和 36.4Hz、36.5Hz边频成分，5.3Hz和5.9Hz与高速级主动轮的转频4.832Hz接近，18.1 Hz和18.7Hz与输出轴转频18.2Hz接近，10.7Hz和36.4Hz、36.5Hz分别与高速级主动轮转频和输出轴转频的二倍频接近。493.9Hz对应波峰的幅值较大，可能为与某频率波峰重合所致。上述边频所对应频率波峰幅值相对于载波频率波峰的幅值较高，故存在故障。为认清故障特征，对高速级啮合频率附近频带做解调谱分析，分析结果如图4所示。

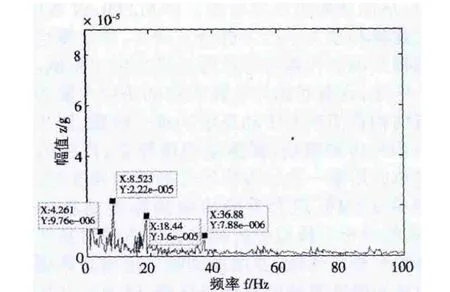
图4 高速级啮合频率处解调谱

从图4可看出，主要的调制频率为4.461Hz、8.523Hz和18.44Hz、36.88，其中4.461Hz正好与高速级主动轮转频接近，8.523Hz与主动轮转频的二倍频接近，18.44Hz正好与输出轴的转频接近，36.88Hz为输出轴转频的二倍频。其中8.523Hz为主要的调制频率，初判断故障出现在高速级主动轮或其所在轴不对中。由于该齿轮传动系统的故障有可能为多故障并发状态，所以不能简单地从故障机理识别出故障特征[6]，为进一步准确识别故障，需对轴不对中故障的齿轮传动系统进行动力学模拟，以提取轴不对中故障的振动信号特征，验证对上述故障的判断。

2 轴不对中的动力学模拟信号分析

2.1 齿轮传动系统三维模型的建立 齿轮传动系统共有三个速度级：低速级和中速级是行星轮系，高速级为平行轴轮系，其中低速级和高速级各包括一个外齿圈，三个行星轮，一个太阳轮；高速级包括一个主动轮的齿轮和一个从动轮的齿轮。根据齿轮传动系统的工作条件及主要的设计参数进行选择和配置[8]。设置各齿轮参数如表1所示。建立三维模型如图5所示。

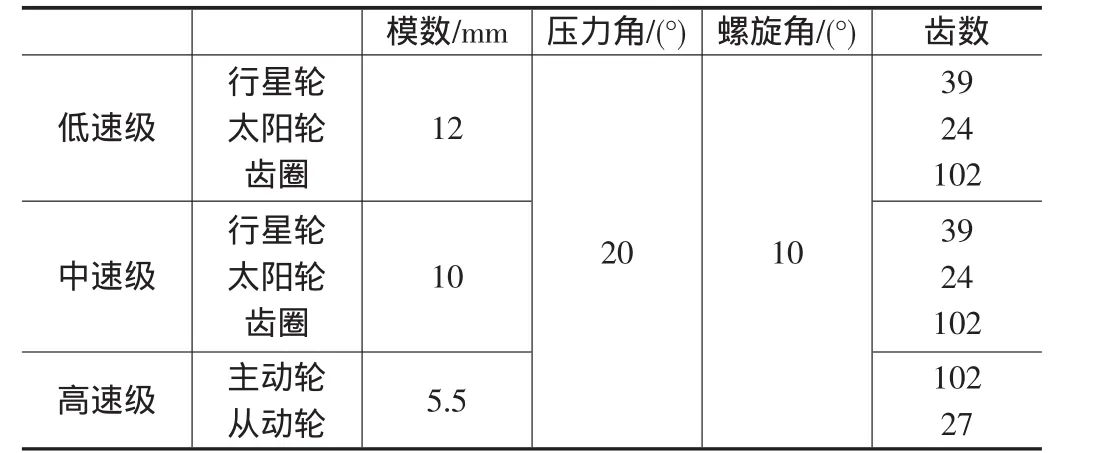
表1 齿轮传动系统齿轮参数

图5 齿轮传动系统整体装配图

2.2 正常状态的模拟信号分析 将图5所示的齿轮传动系统装配体模型导入到ADAMS中，设置好相应的运动副，并在主轴处设置驱动，主轴的转速为10.5r/min，在ADAMS驱动速度设置中，转速大小设置为63°/s。计算求得模拟信号功率谱如图6所示。从图6中可知，波峰对应频率4.827Hz对应中速级太阳轮转频4.823Hz；18.12Hz，对应高速级主动轴的转频18.2Hz；92.34Hz对应中速级啮合频率93.72Hz，且182.6Hz、276.3Hz为92.34Hz的二倍频和三倍频，其幅值依次减小；487.1Hz对应高速级啮合频率，979.2Hz、1471Hz分别为487.1Hz的二倍频和三倍频，且其幅值也依次减小。分析可知，模拟得到的信号特征与正常状态齿轮振动信号特征相符[9]。

图6 正常状态下模拟信号功率谱

2.3 轴不对中故障模拟信号分析 在ADAMS中模拟轴不对中故障状态。轴不对中设置在中速级太阳轮与高速级主动轮的联轴器处。模拟轴不对中故障信号功率谱如图7所示。

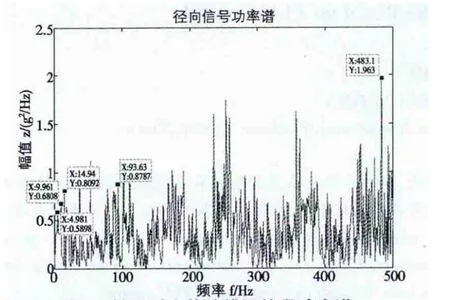
图7 轴不对中故障模拟信号功率谱

对高速级啮合频率481.4Hz处做细化谱，得到图8所示细化谱。

图8 481.4Hz处细化谱

从图8可以看出，模拟信号所反映出的齿轮高速级啮合频率为483.6Hz。其高速级主动轴的转频为4.823Hz，图中483.6Hz的边频成分有479.6Hz和488.7Hz，473.6Hz和493.7Hz。与483.6Hz的频率差分别为5Hz和10Hz。考虑到模拟信号计算精度和误差，可认为该边频为高速级主动轴的转频和及其二倍频与高速级啮合频率调制的成分。对483.6Hz附近的频带求解调谱，如图9所示。

图9 高速级啮合频率附近频带解调谱图

由图9可以看出，解调谱上有两个主要调制频率，分别为4.9Hz和10.3Hz，其中10.3Hz的幅值最大，为主要调制频率。根据文献[7]，齿轮轴不对中故障的信号特征为以齿轮啮合频率和它的谐波为载波频率，齿轮所在轴转频和它的倍频为调制频率的啮合频率调制，其中调制频率的二倍频成分幅值最大。说明所模拟得到的轴不对中故障特征合理。通过对比图9所示的模拟信号高速级啮合频率附近频带的解调谱和图3所示实验信号高速级啮合频率附近频带的解调谱，可以发现二者所反映出的主要调制频率均为高速级主动轮所在轴转频的二倍频，其振动信号特征基本一致，说明对齿轮传动系统的高速轴不对中故障的判断是正确的。

3 齿轮传动系统各故障状态分形特征

若对上述齿轮传动系统的不同状态能用分形维数进行区别的话，就可以将其分形维数作为齿轮传动系统的故障特征量，用于其故障的诊断识别。为了分析比较分形维数对不同故障状态的反映程度、对不同方法得到的同种故障状态的反映程度，建立下述五种状态信号。

对（a）图6所示的正常状态模拟信号功率谱，（b）图7所示轴不对中模拟信号滤波后的功率谱，（c）图3所示轴不对中实验信号滤波后的功率谱，（d）轴不对中模拟信号滤波前功率谱，（e）轴不对中实验信号滤波前五种状态的功率谱进行分形维数计算。

3.1 时间延迟的计算 用自相关函数法[10]分别计算五种状态信号功率谱的时间延迟，得到τ=4。

3.2 嵌入维数m的计算 当嵌入维数大于等于某个数值时，所对应的关联维数就收敛于某一固定数值，此时使关联维数收敛的最小嵌入维数就为计算所用的嵌入维数[11]。对上述五种状态的功率谱计算得到m=361。

3.3 关联维数计算 对五种信号的功率谱分别取25段，计算其关联维数分别为 a，d，e，b，c，计算结果如表 2 及图10。

图10 关联维数图

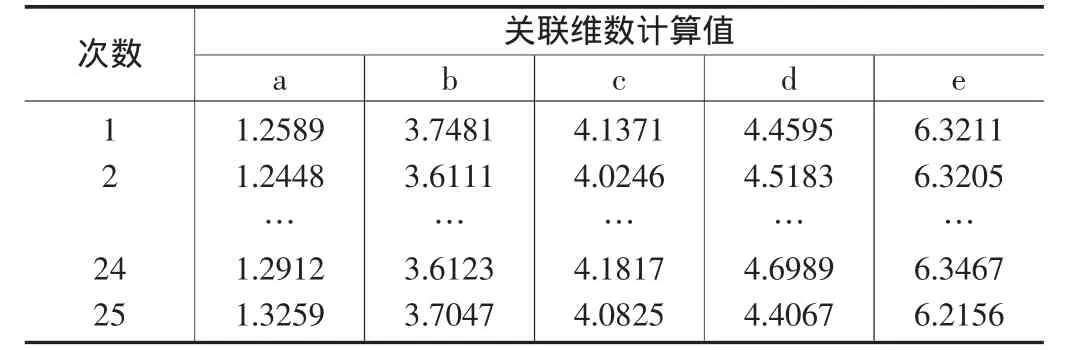
表2 五种状态下关联维数计算结果

从表2及图10的计算结果可以看出，（a）正常状态模拟信号功率谱的关联维数为1.2745±0.2；（b）轴不对中模拟信号滤波后的功率谱的关联维数为3.6111±0.2；（c）轴不对中实验信号滤波后的功率谱的关联维数为4.1141±0.2，（d）轴不对中模拟信号滤波前的功率谱的关联维数为4.5317±0.2；（e）轴不对中实验信号滤波前的功率谱的关联维数为6.3127±0.3。因为（a）正常状态模拟信号功率谱的主要频率成分为啮合频率及其倍频成分，以及轴的转频成分，且在主要的频率成分周围无明显的边频成分，所以关联维数最小；（b）轴不对中模拟信号滤波后的功率谱除了具有正常状态的频率成分外，还有复杂的边频成分，其维数比正常的高；（c）与（b）的故障状态虽然相同，但（c）实验信号由于噪声等干扰的影响，其信号成分要较（b）的复杂，所以，维数略高于（b）。状态（d）和（e）都是滤波前的轴不对中信号，状态（d）的成分较（e）的成分少，所以维数较低。（e）除了具有（c）的成分外，还有其他速度级的啮合频率与边频等复杂成分，因此其关联维数最大。

通过以上分析可知，关联维数的大小能反映出振动信号功率谱中频率成分的复杂程度。故障越复杂，其功率谱的成分越复杂，关联维数则越大。关联维数的大小可说明故障的位置及复杂程度。

4 结论

对实验信号采用功率谱，细化谱，解调谱相结合的分析方法，可初步诊断出齿轮传动系统高速级轴不对中故障；并用动力学模拟方法，在ADAMS中建立轴不对中故障的齿轮传动系统动力学模型，通过动力学模拟计算提取分析振动信号故障特征，验证了对实验信号故障类型及故障位置诊断的准确性。说明通过模拟分析验证对实验信号诊断的方法可有效提高复杂机械系统故障诊断的准确性、可靠性。通过对实验信号和模拟信号滤波前后的功率谱所计算的关联维数，发现齿轮传动系统不同状态的关联维数，能反映出其不同状态振动信号成分的复杂程度，可作为其故障特征量识别复杂故障的位置及其程度。

[1]高学敏.风力发电机组传动系统的研究[D].华北电力大学，2007：1-9.

[2]陈雪峰，李继猛等.风力发电机状态监测和故障诊断技术的研究与进展[J].机械工程学报，2011,47(9):45-52.

[3]唐新安，谢志明，吴金强等.风力机齿轮箱故障诊断[J].噪声与振动控制，2007(1)：120-124.

[4]BARSZCZ T，ROBERT B.Application of spectral kurtosis for detection of a tooth crack in the planetary gear of a wind turbine[J].Mechanical Systems and Signal Processing,2009(23)：1352-1365.

[5]HUANG Qian，JIANG Dongxiang，HONG Liangyou，et al.Application of wavelet neural networks on vibration fault diagnosis for wind turbine gearbox[J].Lecture Notes in Computer Science，2008，5264：313-320.

[6]INALPOLAT M，KAHRAMAN A.A theoretical and experimental investigation of modulation sidebands of planetary gear sets[J].Journal of Sound and Vibration，2009，323：677-696.

[7]王志新.现代风力发电技术及工程应用[M].北京:电子工业出版社,2010.

[8]余志林.基于UG的齿轮参数化建模系统[J].东华大学学报(自然科学版).2008,34(3):326-331.

[9]丁康,李巍华,朱小勇等.齿轮及齿轮箱故障诊断及实用技术[M].北京:机械工业出版社,2005.

[10]Abarbanel,H.D.I.,Analysis of Observed Chaotic Data,Springer-Verlag,New York,1996.

[11]张朝曦,傅强,钟纪华等.基于G-P算法计算关联维的讨论[C].第十二届全国非线性振动暨第九届全国非线性动力学和运动稳定性学术会议论文集,天津：天津大学出版社，2009.