基于水文因素的尾矿坝变形监测分析研究*

陈志华，施 昆，史华林

(1．中国有色金属工业昆明勘察设计研究院，云南 昆明 650051;2．昆明理工大学，云南 昆明 650093)

0 引言

按照规范规定［1］，对一些重要监测项目提出预计的测值变化范围，提出设计监控指标;对于坝体位移监测、浸润线监测及安全检查的资料必须进行分析。对监测数据进行变形分析可采用卡尔曼滤波［2］、灰色理论及小波分析［3］等数学模型，也可采用常规分析方法中的多元线性回归进行变形分析。

引起尾矿坝变形的因素很多，也很复杂［4］;浸润线、库水位就是引起尾矿坝变形的两个很重要的水文因素。

渗水在水位作用下，水流渗入坝体，将坝体分为上干下湿两部分，干湿尾沙的分界线即为浸润线。浸润线的变化标志着坝体含水量的多少，由于土体的变形与其含水量有密切关系，所以，浸润线是引起尾矿坝变形的一个很重要的水文因素;同时，库水位的变化直接影响土坝浸润线位置的变动，因而也影响土坝体的变形值［5］。

因此，尝试以浸润线、库水位这两个水文因素作为尾矿坝变形分析的外因，采用多元线性回归分析的方法，对浸润线、库水位的变化与尾矿坝的变形进行分析研究，从中得出浸润线、库水位水文因素对尾矿坝变形的影响关系是尾矿坝变形分析的一种新途径。

1 多元线性回归分析原理及模型建立

1．1 多元线性回归分析原理

通过分析所观测的变形量和外因(引起变形的因素，一般是多元的)之间的相关性，来建立外因与变形之间关系的数学模型［6］。

式中:t=1，2，…，n，εt∈N(0，σ2)，其中，下标t 为观测值变量，共有n 组观测数据，p 表示因子个数。

在矿山尾矿库变形监测分析中，将时间、变形量与浸润线三元结合起来建立时间、浸润线与变形数学模型来进行变形分析及预测，将时间、变形量与库水位三元结合起来建立时间、库水位与变形数学模型来进行变形分析及预测。

1．2 多元线性回归分析模型建立

1．2．1 变形量、时间及浸润线三元模型

由变形量D、时间t、浸润线r 建立如下模型［7］:

根据时间、浸润线及变形量(三维中的任一维，如X 方向位移)建立线性方程组，利用间接平差原理［8］解算出a0、a1、a2、a3、a4、a5六个模型参数来确定模型。

1．2．2 变形量、时间及库水位三元模型

由变形量D、时间t、库水位w 建立如下模型:

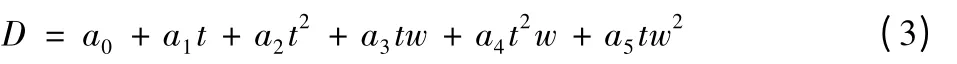
根据时间、库水位及变形量(三维中的任一维，如X 方向位移)建立线性方程组，利用间接平差原理解算出a0、a1、a2、a3、a4、a5六个模型参数来确定模型。

1．3 回归方程及系数的显著性检验

采用F 检验对上述多元回归分析模型及其系数进行显著性分析，回归分析模型的统计量可用式(4)求得，模型系数的统计量用式(5)求得。而相关系数Cov 可反映模型与实际情况的相关程度，可用式(6)计算:

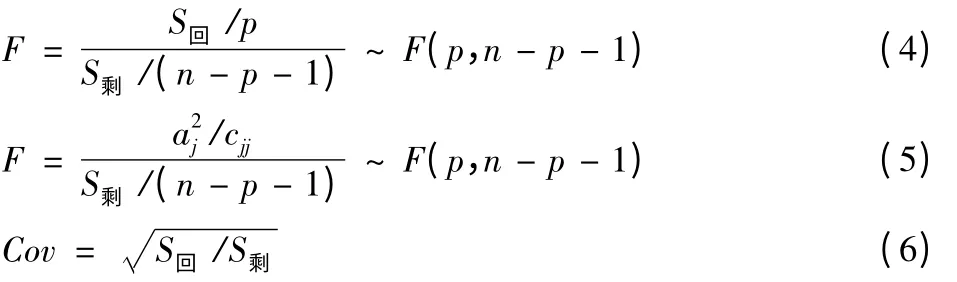
式中:S回为回归平方和;S剩为剩余平方和;n 是观测值个数;p为因子个数;aj为模型系数;cjj为法方程系数矩阵的逆矩阵(xTx)-1的对角线元素。

2 实例分析

以滇中地区某铜矿的尾矿库实时在线监测为例。该尾矿库地处高山区域，地势为北高南低，两岸多为陡峭的岩壁，极少部分为坡地，坡地植被发育，区域内水文地质条件复杂，地下水类型较齐全，以基岩裂隙水分布最广，碳酸盐岩类裂隙溶洞水次之，松散岩类孔隙水面积较小，主要分布于山间洼地和宽谷。

根据尾矿库安全管理监测要求，对该尾矿库共布设GPS2035 -0、GPS2053 -0、GPS2053 -1、GPS2053 -2 等4 个GPS实时在线监测点，以监测尾矿坝的三维变形量。其中，对GPS2035 -0 和GPS2053 -0 两点进行了浸润线观测;对该尾矿库的库水位、干滩和雨量等进行监测;对尾矿坝的内部倾斜进行监测。

以下采用多元线性回归分析的方法，对该尾矿库的浸润线、库水位的变化对尾矿坝的变形的影响进行分析。

2．1 基于浸润线的回归分析实例

以监测点GPS2035 -0 的X 方向累计位移量进行浸润线分析，计算数据及估值分析结果，如表1 所示。

估值分析过程为:

1)显著水平0．900，F(5，5)= 0．289605

显著水平0．900，F(1，5)= 0．017470

2)模型参数及回归系数显著性检验:

a0 = 0．108684248

F0 = 0．000210

a1 = 16．196713133

F1 = 9．460905

a2 = -2．195581932

F2 = 6．651043

a3 = 0．007143731

F3 = 0．348892

a4 = 0．004662851

F4 = 2．214967

a5 = -0．000077509

F5 = 0．739957

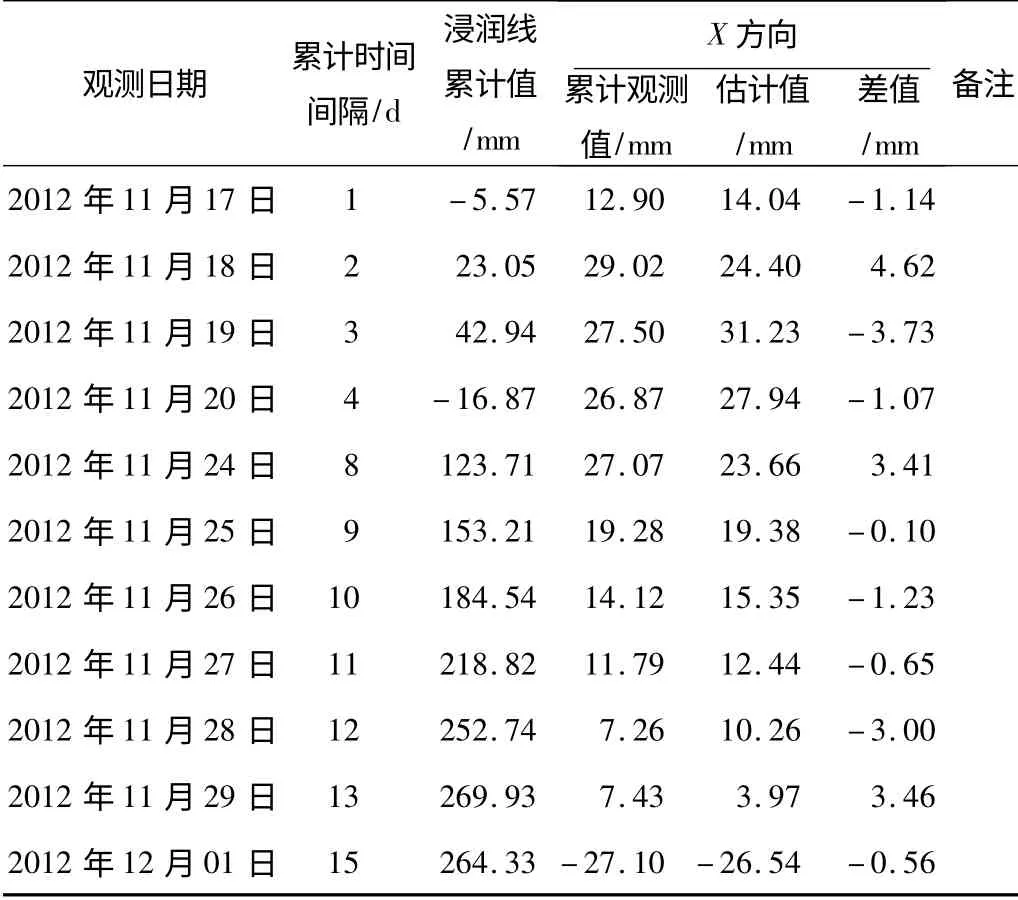
表1 浸润线回归分析实例数据表Tab．1 The infiltrate line regression analysis instance data

3)回归方程显著性检验:

回归平方和 2483．117203

回归方差 496．623441

剩余平方和 72．568070

剩余方差 14．513614

离差平方和 2555．685273

标准误差 3．809674

F 检验统计量 34．217766

相关系数 0．985700

4)模型为:

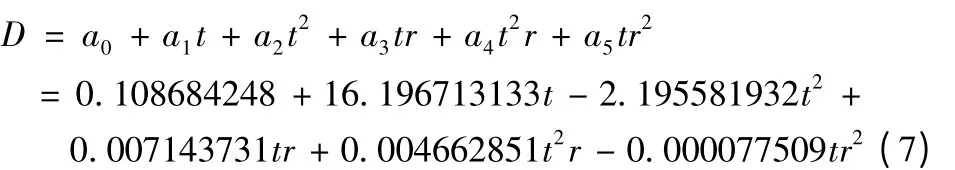
由分析结果来看，相关系数非常接近1，表明X 方向累计位移量与浸润线及时间存在明显的相关性，需要时可以根据所建立的模型从浸润线角度对位移量进行预测。

例如，用所建立的模型式(7)来预测2012 年11 月23 日、11月30 日X 方向累计位移量，如表2 所示。

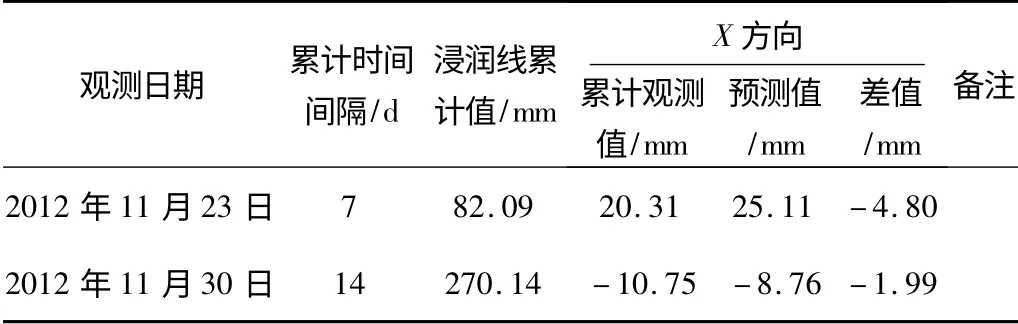
表2 浸润线回归分析表Tab．2 The infiltrate line regression analysis table

从表2 中可以看出:预测值与实测值相差较小，说明建模方法正确，所建模型具有一定的参考价值。

2．2 基于库水位的回归分析实例

以监测点GPS2035 -0 的X 方向累计位移量进行库水位分析，计算数据及估值分析结果，如表3 所示。

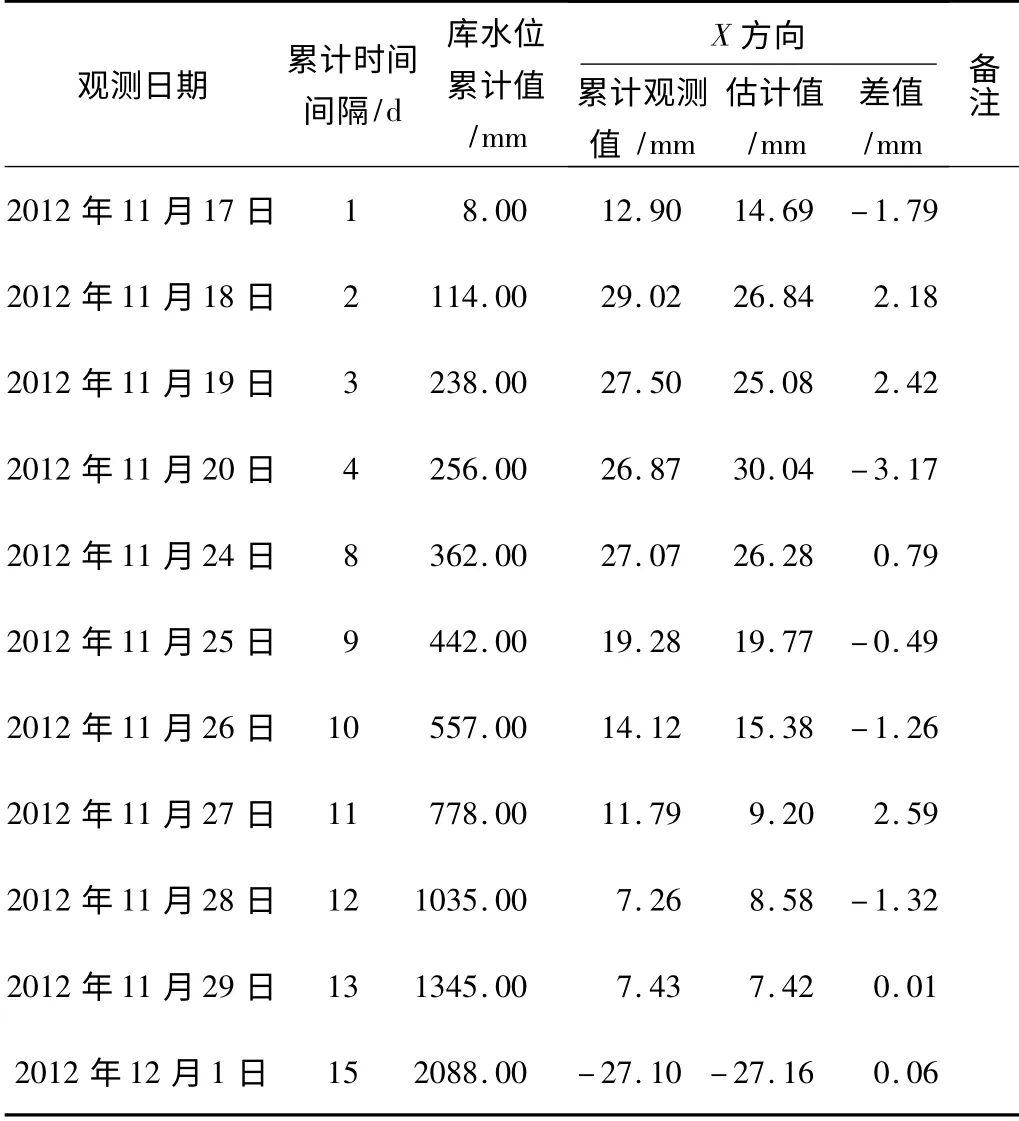
表3 库水位回归分析实例数据表Tab．3 The water level regression analysis instance data

估值分析过程为:

1)显著水平0．900，F(5，5)= 0．289605显著水平0．900，F(1，5)= 0．017470

2)模型参数及回归系数显著性检验:

a0 = -11．907332324

F0 = 2．527342

a1 = 29．666375411

F1 = 17．747896

a2 = -2．685802626

F2 = 22．916768

a3 = -0．053849185

F3 = 7．711682

a4 = 0．006353861

F4 = 9．622400

a5 = -0．000017653

F5 = 11．736529

3)回归方程显著性检验:

回归平方和 2520．942975

回归方差 504．188595

剩余平方和 34．742298

剩余方差 6．948460

离差平方和 2555．685273

标准误差 2．635993

F 检验统计量 72．561204

相关系数 0．993180

4)模型为:

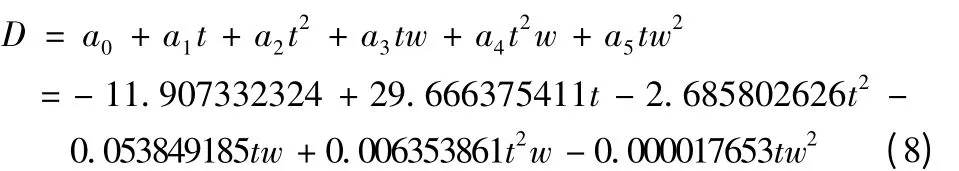
由分析结果来看，相关系数非常接近1，表明X 方向累计位移量与库水位及时间存在明显的相关性，需要时可以根据所建立的模型从库水位角度对位移量进行预测。

例如，用所建立的模型式(8)来预测2012 年11 月23 日、11月30 日X 方向累计位移量，如表4 所示。

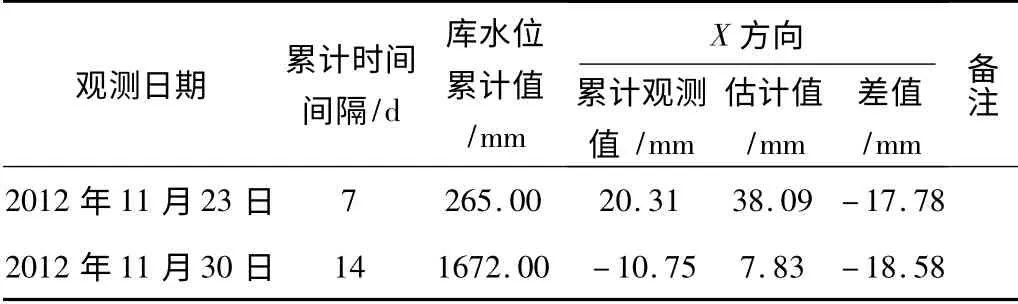
表4 库水位回归分析表Tab．4 The water level regression analysis table

从表4 中可以看出:预测值与实测值相差较大，这是因为库水位受风力等自然界影响较大，监测数据很难达到较高精度;因此，由变形量、时间、库水位建立的模型精度达不到由变形量、时间、浸润线建立的模型精度，也就是说由变形量、时间、浸润线建立的模型更具有参考价值。

3 结束语

浸润线、库水位是引起尾矿坝变形的两个很重要的水文因素。一方面，浸润线的高低标志着土石坝体含水量的多少，坝体含水量的多少又与其变形关系密切;另一方面库水位的变化直接影响土石坝体浸润线位置的变动，因而也影响土坝体的变形。

采用多元线性回归的分析法法，由变形量、时间、浸润线可建立分析预测数学模型;同样，由变形量、时间、库水位也可建立分析预测数学模型。但是，鉴于浸润线监测技术比较成熟，监测数据精度较高，而库水位受风力、尾矿排放量等外界因素影响较大，监测数据很难达到较高精度;因此，由变形量、时间、浸润线建立的数学模型精度高于由变形量、时间、库水位建立的数学模型精度。从实例分析得出，由变形量、时间、浸润线建立的数学模型得到的预测值与实测值相差较小，而由变形量、时间、库水位建立的数学模型得到的预测值与实测值相差较大，这说明由变形量、时间、浸润线建立的模型比由变形量、时间、库水位建立的数学模型更具有参考价值。

［1］ 王运敏，项宏海，汪斌，等．尾矿库安全监测技术规范［S］．北京:国家安全生产监督管理总局，2011:9．

［2］ 修延霞，候凯． 卡尔曼滤波在大坝变形中的应用［J］． 城市勘测，2010(1):92 -94．

［3］ XIAO Jie，ZHANG Jin．Analysis and application of automatic deformation monitoring data for buildings and structures of mining area［J］．Transactions of Nonferrous Metals Society of China，2011，21(S3):516-522．

［4］ 郭朝阳．尾矿库坝体变形规律初探［J］． 中国高新技术企业，2009(15):43．

［5］ 张培基．水坝变形观测［M］．北京:测绘出版社，1981:21．

［6］ 黄声享，尹晖，蒋征． 变形监测数据处理［M］． 武汉:武汉大学版社，2003:110 -112．

［7］ 张勇．不同地方基准转换数值分析的计算研究［D］． 昆明:昆明理工大学，2008:35．

［8］ 武汉大学版社测绘学院测量平差学科组．误差理论与测量平差基础［M］．武汉:武汉大学出版社，2003:102 -106．