物质材料的结构预测和光物理性能模拟
熊玉辉
(河南省驻马店农业学校,河南驻马店,463000)
0 引言
从20 世纪60 年代到现在,非线性光学的发展,成为了当今的领先科技之一。非线性光学材料因为很快的响应速度、多样的化学结构修饰及很高的光学损伤阈值,被广泛应用在各个行业中。但当一种新材料从研发到投入市场,历经设计、实验、论证、制造再到投入市场,一般需要大量反复的实验。而对物质材料进行结构预测,进行光物理性模拟,大大缩短了新材料投入市场的时间,不仅能够节约时间精力,更是节省了资金投入,对非线性光学的发展来说具有非常重大的实际意义。
1 非线性光学材料
分析结构和材料晶体结构的可靠预测结果是非线性光学材料成功设计的关键,然后获取材料信息对物理性能进行模拟。现如今,非线性光学材料有了很大的发展,已经从宏观的块材料扩展到了纳米材料、超材料。其中宏观的块材料是常规的非线性光学材料。应用最多、发现最早的是无机非线性光学晶体,如曾经被称为“全能晶体”的改性晶体和KTP、LBO 和BBO 晶体,LBO 和BBO 是我国自主研发的晶体。另外,因为非线性光学材料响应快、系数大、可按照需求设计等优点,已经形成了一个非常大的体系。
无机非线性光学材料包括红外材料、紫外材料和可见的红外区材料。紫外材料通常采用的是硼钠盐晶体;红外材料通常采用的是半导体材料;可见的红外区材料通常采用的是铌酸盐、磷酸盐和碘酸盐。无机非线性光学材料很稳定,所以支持异性离子交换,使得无机非线性光学材料比有机晶体纯度高。
微结构非线性光学材料即纳米材料,因为其本身加工手段具有限制性,所以这种材料出现的比较晚。但微结构非线性光学材料具有常规材料所没有的特性,显现出极强的光学效应,所以近年来,微结构非线性光学材料飞速发展,已经取得了非常大的进展。
超材料属于新型非线性光学材料,是指人工合成的、具有自然界材料所没有的奇异物理特性材料,如电磁感应透明材料、人工电磁复合材料、负折射率材料和特异超材料等。因为超材料的特异性,所以对物质光学非线性能力有很大的提升。
目前,大部分的材料研究发展都是通过观测和实验来完成的,重复耗时的实验使得新材料的应用要花费大量的时间,但实际上,有些实验可以通过计算分析来完成,计算分析为新材料的发现开辟除了一个经济、省时的方法,而且减少了对于物理实验的依赖性。准确建立材料性能模型,通过计算分析,从理论和实际的实验来论证模型正确性,这样新材料的研发周期将大大缩短。
2 结构预测
对物质材料的结构预测是新材料成功研制的有效途径,是材料广泛应用的关键,准确的预测材料结构具有非常大的意义。
2.1 分子结构的预测
分析结构预测中最常见的方法就是能量最小化方法,也称为几何优化或能量优化。能量最小化就是在分析处于稳定的体系状态时,对势能面局部和全局的最小值。能量最小化通过数学优选过程对原子进行移动,减小对非平衡分子的几何构成的原子作用力,持续到原子净作用力趋近于零。结构优化不同,反应物的热化学性能、异构化反应和构象稳定性都不同。所以,输入的最初分子结构模型在优化时越合理,越能对原子移动和净作用力的速度有所提高,从而完成能量最小化。
以2009 年中科院实验人员研发的新型材料——金属内嵌富勒烯结构为例,对分析结构进行分析预测。金属内嵌富勒烯结构类似于俄罗斯套娃,研发成果最初发表在《美国化学会会志》上,引起了世界各国的广泛关注。作为一种新型结构的具有光电特性的特殊分子,金属富勒烯是把金属原子内嵌到富勒烯碳笼而形成的,一个富勒烯碳笼可以嵌入多种金属原子,如金属碳化物团簇、同核或异核双金属团簇、单金属原子、金属氧化物团簇和金属氮化物团簇等。因为具备金属富勒烯碳笼这个优良的特性,金属富勒烯在各个行业有着广泛的应用空间和发展潜能,所以对金属内嵌富勒烯结构的预测具有重要意义。
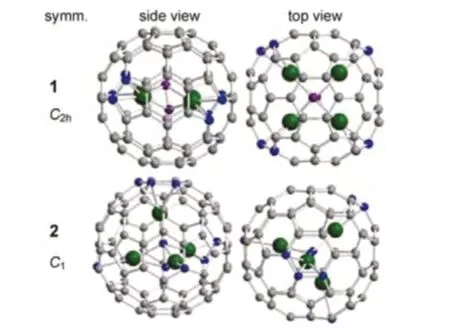
图1 通过BLYP/DNP 结构优化得到Sc4C2@C80-Ih 同分异构体图
如图1 所示,在Sc4C2@C80-Ih的异构体中,异构体1 里4 个Sc 原子形成的四角形包围着C2基团;在异构体2 中,Sc4四面体的中心就是C2。通过BLYP/DNP 计算出最大的在异构体2 中,Sc4C2绕C80的C2旋转,最大的转动势垒为2.8kcal/mol,因此得出在室温的条件下,在C80笼里的Sc4C2可以自由的旋转。通过研究证实,C2基团内嵌在Sc4内,即C2@ Sc4,而C80又包围着C2@ Sc4,从而构成C2@ Sc4@C80三层嵌套结构。
金属内嵌富勒烯结构Sc3CN@C80-Ih就是通过BLYP/DNP 结构优化得到。3 个Sc 基团包围着NC 基团,N 原子在基团中心,C原子在Sc 三角形的一个边上,这5 个原子构成一个对称的平面;N 原子在Sc 三角形的一个边上,C 原子在基团中心,结构比较稳定。通过计算表明,CN(NC)基团价态是CN3-,和Sc3+构成共价配键,从而得到整个稳定价态分布为([SC3+]3[NC]3-)6+@(C80)6-。
2.2 晶体结构的预测
晶体结构的预测主要有两种,全程探测法和化学直觉法。化学直觉法根据经验通过数据的挖掘来预测晶体结构,它的优势在于通过化合物的相关性和晶体结构的特性很好的来预测晶体结构,能够有效的节省计算资源,但缺点是对于稳定存在但没发现的结构类型需要做大量的细致工作才能解决;全程探测法是在能量表面进行的预测,它完全不需要以往知识和实验数据,仅需要知道化合物成分,就能采取不同的数学模型进行处理。全程探测法又可以细分为超动态法、极小跳槽法和进化算法等。
如应用在USPEX 编码中的进化算法,在1400 个结构进化和22 代繁衍后,预测非线性光学材料Ba2BilnS5的晶体结构,在计算优化后,在探测晶体的过程中,发现Ba2BilnS5的两个异构体亚稳态晶体结构,如表1 所示,为三种结构单胞参数。通过比较可以得出,实验数据和理论预测完全一致。
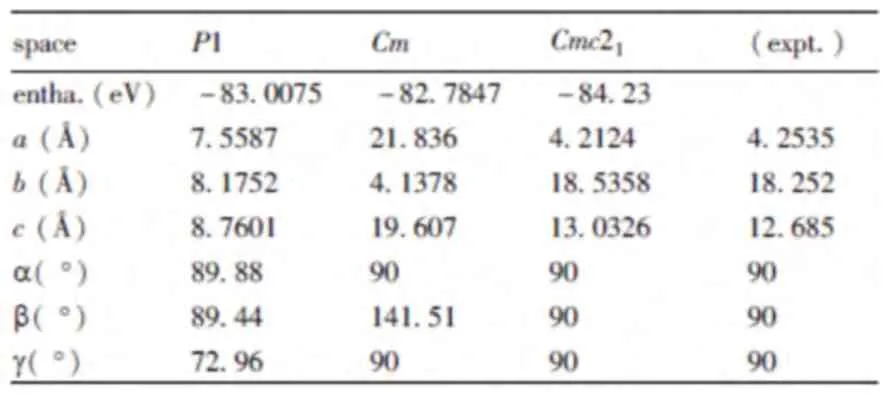
表1 实验结构和预测的单胞参数
3 光物理性能模拟
3.1 离子晶体光物理性能模拟
对于离子晶体来说,根据第一性原理的固体能带理论,对晶体电荷分布、态密度和能带结构进行计算,再结合在扩展体系的非谐振子模型的光学性能,建立电子运动方程,从而导出在一阶级化率和高阶级化率非线性材料的关系。这种模型适用于研究高阶宏观极化率在低频光子输入时的性质,而对于双光子和单光子共振的情况以及一阶级化率和高阶级化率的比例不能准确的计算的情况是不适用的。
举例说明Cd4BiO(B03)3晶体二阶倍极化率的模拟。Cd4BiO(B03)3晶体即CBOB,它是根据典型非谐振子模型,二阶倍极化率如下公式:
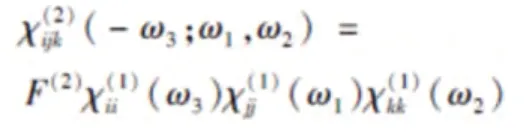
其中,a:二阶非线性光响应参数;e:电荷数;m:电子的质量;N:晶体中一个单胞的密度。节点函数的虚部为:
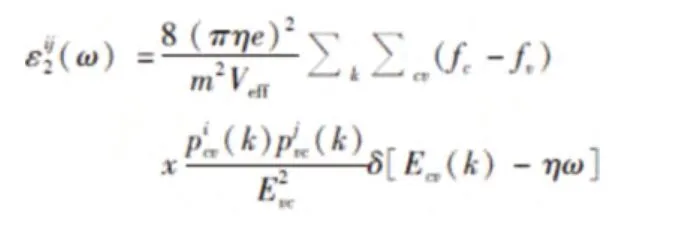
其中,fc:导带分布函数;Fv:价带费米能级分布函数;Veff:晶胞体积; :动量矩阵元。通过转换得到:

在实际计算过程中,应用CASTEP 软件,CBOB 结构参数进行输入后得到能带结构,再对介电函数虚部进行计算,最终得出CBOB 晶体倍频系数与频率的关系。
3.2 分子晶体光物理性能模拟
对于分子晶体来说,要先对局部或个别分析非线性光学性质进行计算,然后对分子光物理性能辅以校正,最终得到块体的光物理性能。一般情况下,采用态求和、响应理论和适用有限场来计算分子非线性光学性质。态求和是其中比较常用的一种方法,态求和在计算过程中具有几个特点:一是可以计算动态非线性光学性质或频率相关性质;二是对于能够有效地诊断出对性质有重要贡献的的基团;三是可以相互了解激发分析波函数多电子的性质。
以2-羧酸4-硝基吡啶-1-氧(POA)晶体二阶光物理性能模拟为例,实验得到两种晶体,两种晶体结晶形式不同、空气群相同。以晶体结构为分子簇输入坐标,以分子簇为计算单位,利用密度泛函理论得出分子簇单点的能量,进而计算激发态性质。采用态求和,计算二阶非线性光学参数如下列公式:
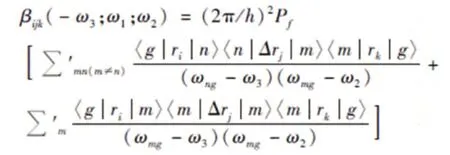
其中,Pf:3 坐标与3 频率捆绑一起的6 置换和的平均值。可以利用BGP 软件程序进行计算, BGP 软件程序可以完成三光子、双光子、二阶、三阶吸收截面的模拟计算,所以直接输入式中需要的参数,很方便就能得到二阶非线性光学系数和分子簇电子结构。其中采用的是TDDFT 方法得到激发态波函数,然后计算激发态波函数的矩阵积分得到激发态间的跃迁偶极矩。
4 结语
本文介绍能量最小化和金属内嵌富勒烯Sc3CN@C80-Ih 结构预测,使用CASTEP 和密度泛函数论软件,对2-羧酸4-硝基吡啶-1-氧(POA)晶体二阶非线性光学性质、Cd4BiO(B03)3晶体二阶倍极化率进行模拟。现如今,对物质材料做出可信的预测并模拟出仍然是一件有很大难度的课题,但随着科技的不断发展,相信在不久的将来,从理论和实际都能验证预测的准确性,有效的减少材料的研发时间和费用,将会对物质材料的发展具有重大的意义。

图2 分子簇的倍频系数β 相对数据的收敛
[1]林晨升,程文旦,张炜龙,张浩,何长振.物质材料的结构预测和光物理性能模拟[J].化学进展.化学进展,2012,6.
[2]孙玉玲,王新,刘杰,蒋新星,孙瑾.非线性光学材料研究现状与应用前景[J].华工科技,2011,5.
[3]叶成,胡汉杰.有机及聚合物非线性光学材料[J].中国科学基金.
[4]吴长峰.硅及稀土材料低维纳斯结构的组装和光物理性质[J].武汉大学学报,2011.10.
[5] 姜玮,温全武,田华,马松梅.非线性光学材料进展[J].甘肃科技;2006 年08 期

