多级离心泵径向导叶内压力的脉动特性

刘厚林，周孝华，王凯，毛陆敏

(1. 江苏大学 流体机械工程技术研究中心，江苏 镇江，212013；2. 扬州长江水泵有限公司，江苏 扬州，225200)

多级离心泵广泛应用于电力、石油化工、矿山、冶金、造纸等领域。随着多级泵机组单机容量的不断增大，机组效率和稳定性愈加重要。离心泵内的动静干涉等因素可能引起泵内压力脉动，严重影响离心泵运行的稳定性[1-2]。国内外有关离心泵的研究主要以理论分析、性能试验和多级泵单级CFD 模拟为主[3]。谈明高等[4]对八级蜗壳式离心泵进行水力设计，并进行了外特性试验研究；张人会等[5]采用响应面方法对离心泵叶轮进行了优化，并通过数值求解多维空间上偏微分方程的边值问题对叶片进行优化，实例结果证明其方法是合理的；赵运革等[6-7]对多级离心泵全流量进行了性能预测，并分析了其内流特性；蒋庆磊等[8]对多级离心泵的次级叶轮与导叶进行了模拟，并分析了叶轮4 个相位点的压力脉动变化规律；孔繁余等[9]对两级离心泵进行了压力脉动分析，得到蜗壳内的压力脉动比首级要明显，且蜗壳内压力脉动最大值出现在隔舌附近；Kawata 等[10-12]对泵内部不稳定的动态特性进行了研究。目前关于多级泵非稳态模拟计算的文献已较常见，文献多数采用单级模拟，并通过计算得到整机的外特性和瞬态的非定常特性，但多级泵内流流动相对复杂，依此方法难以真实地反映多级泵内部的非定常特性。到目前为止，尚未发现对多级离心泵整机瞬态特性研究的相关文献报道。为此，本文作者采用CFX 软件对五级离心泵整机进行全三维非定常数值计算，监测五级离心泵各级导叶单流道进口处的压力脉动，分析各级导叶内压力脉动规律，以期得到更真实的多级离心泵导叶内部压力脉动特征。

1 数值计算

1.1 计算模型及网格划分

计算模型为五级离心泵，流量Q=400 m3/h，扬程H=846 m，转速n=2 950 r/min。其主要几何参数如表1 所示，采用Pro/E 对五级离心泵各零件进行三维造型，其装配分解图见图1。计算网格的合理设计和高质量生成是计算的前提条件，同时也是影响CFD 计算的关键因素之一。由于五级离心泵几何结构比较复杂，采用对复杂边界适应性强的非结构化四面体网格对计算域进行网格划分，划分3 组网格单元总数分别为828.9×104，1 172.1×104和1 426.7×104的四面体网格，对五级离心泵进行网格无关性验证，结果表明在1 100×104以上的2 种网格计算结果效率与扬程误差都在0.6%以内，且趋于稳定，所以选取网格单元数为1 172.1×104进行数值研究，各部分网格单元数如表2所示。

1.2 数值计算方法

采用CFX 软件对五级离心泵内部流动进行数值模拟，模型中的系数均采用默认值，并采用多重旋转坐标系。采用有限体积法对非定常不可压缩N-S 方程进行离散。采用SIMPLE 算法对压力和速度进行耦合，变量残差值的收敛标准设置为10-4。

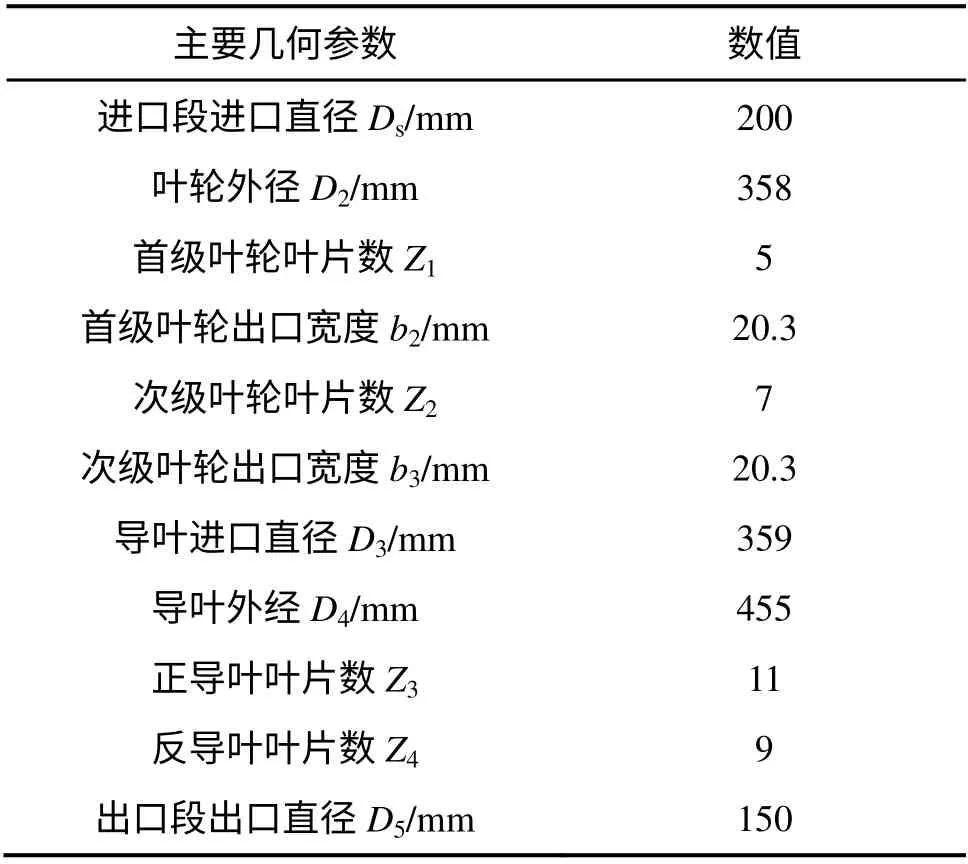
表1 五级离心泵主要几何参数Table 1 Main parameters of five-stage centrifugal pump

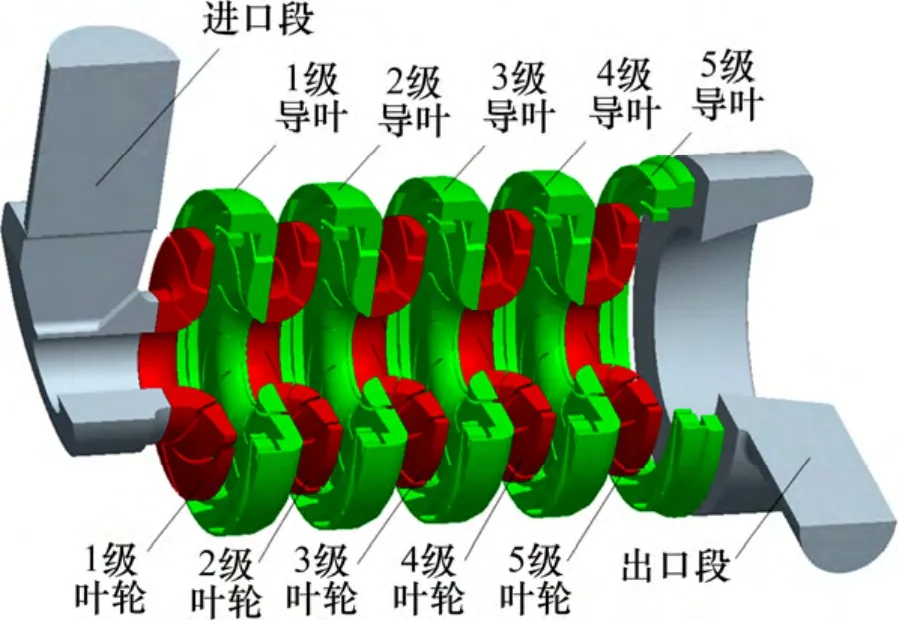
图1 五级离心泵装配分解图Fig.1 Assembly diagram of five-stage centrifugal pump

表2 五级离心泵各部分网格数Table 2 Grid distribution in five-stage centrifugal pump 104个

1.3 边界条件

进口边界取在进口段法兰处，采用质量流量进口，并假设进口的速度分布均匀，流动方向垂直进口平面。出口边界设在出口段法兰处，采用平均静压出口。假设壁面为光滑水力壁面，满足无滑移的壁面边界条件，即时均速度和脉动速度的各个分量均为零，近壁区采用标准壁面函数法处理。

1.4 湍流模型

该泵在设计工况下扬程的试验值为846.3 m，效率的试验值为81.8%。分别采用Standard k-ε，RNG k-ε，Standard k-ω 和SST k-ω 模型对五级离心泵进行数值模拟，并把模拟结果与试验值相对比，结果如表3所示。

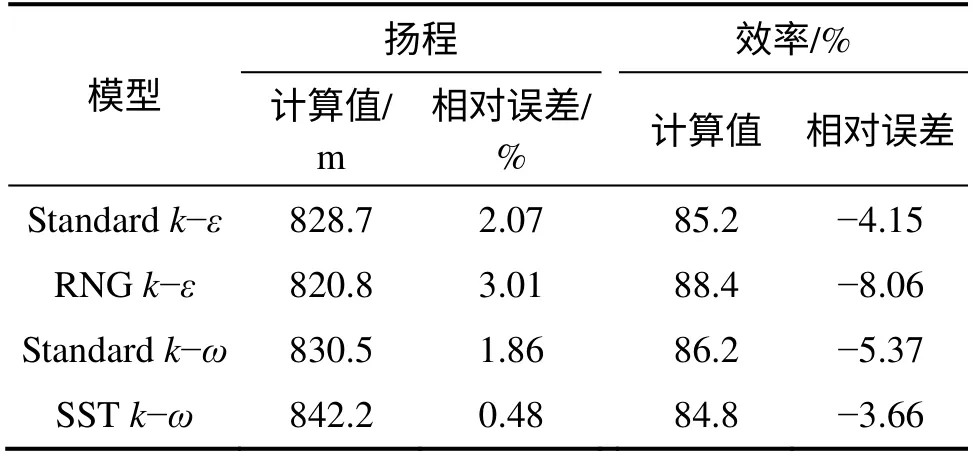
表3 不同湍流模型对比Table 3 Comparison of different turbulence model

由表3 可知：采用4 种湍流模型计算效率均略大于试验值，计算扬程都略小于试验值，可以发现采用SST k-ω 模型的计算扬程和效率与试验值对比误差都在4%以内，数据吻合度较高，可见，该数学模型能较为准确地预测该泵的外特性，为进一步预测分析多级离心泵瞬态性能提供了保证。

1.5 非定常设置

选取SST k-ω 模型定常计算结果作为非定常计算的初始条件，根据叶轮的转速，设置叶轮旋转1 周需120 个时间步长，即叶轮每旋转3°计算1 步，非定常的时间步长为1.695×10-4s。因多级离心泵结构复杂，由叶轮与导叶多级串联而成，叶轮的高速旋转、叶轮与静止导叶之间的动静干涉以及流体的高黏性，导叶内部流动呈现更为复杂的非定常性，这种非定常流动可能引起流场的压力脉动。由于导叶与叶轮的对称性，为研究各级导叶圆周进口处的压力变化情况，在导叶单流道进口直径为0.8D4=364 mm 圆周上(轴向位于正导叶中心平面上)，设置3 个监测点p1，p2和p3，如图2 所示，图2(a)所示为导叶模型二维图，图2(b)所示为图2(a)中导叶进口处局部放大图。令pij表示第i 级导叶内pj点位置，其中i=1，2，3，4，5；j=1，2，3。

2 压力脉动特性分析

为了分析CFD 非定常瞬态模拟出的静压变化，本文把每个位置的静压变化的平均值设置为0。Guelich等[14]在分析压力脉动结果时，为呈现压力脉动的数据的一致性，对每步计算出的静压值进行缩放，引进压力脉动系数Cp，在本文中同时约定压力波动幅度CA。

式中：Δ p 为压力与平均压力之差；ρ 为工作介质密度；u2为叶轮出口处圆周速度。

式中：pmax和pmin都为静压；p总max为所有监测点中静压绝对值中的最大值。

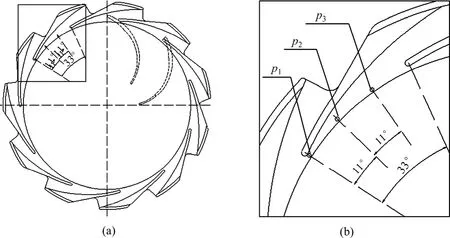
图2 导叶进口处监测点示意图Fig.2 Pressure monitoring points at inlet of diffusers

图3 所示为各级导叶在p1位置点叶轮旋转1 个周期内的压力脉动时域图，横坐标T 表示叶轮旋转1 个周期，纵坐标Cp表示压力脉动系数。从图1 可以看出：该压力脉动随时间变化具有明显的周期性，静压波动变化剧烈，且第2，3，4，5 级压力波动基本同步，并且在短时间内压力迅速地上升与下降，如在第2，3，4，5 级的0.02T 时。其原因是：当叶轮叶片压力面逐渐到达导叶叶片进口处时，压力迅速增加，且在叶轮叶片压力面位于导叶叶片进口处时，压力出现最大值。随叶轮旋转，叶轮叶片吸力面逐渐通过导叶进口处，压力迅速下降并在叶轮叶片吸力面离开导叶进口时达到最小值，随叶轮叶片远离导叶叶片进口，此处压力迅速上升，同时叶轮叶片通过导叶叶片进口时引起的压力迅速的下降与上升，导致瞬间的冲击损失。

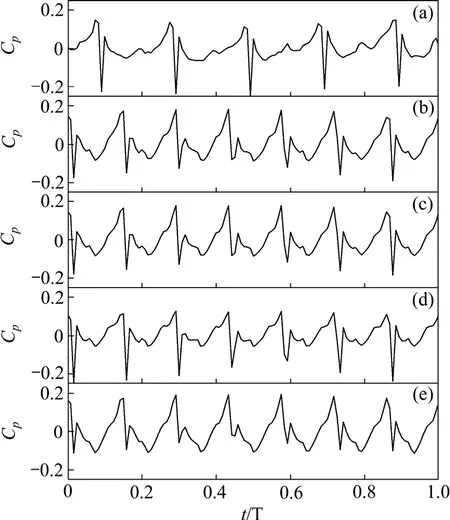
图3 导叶上p1 位置的压力脉动时域图Fig.3 Pressure fluctuations at p1

首级叶轮叶片数与其它级数叶片数不同，直接导致首级叶轮叶片通过频率与其他级数不相同，首级叶轮叶片通过频率F1=245.8 Hz。2，3，4，5 级叶片通过频率为F2=344.17 Hz。图4 所示为各级导叶上p1位置的压力脉动频域图，由图4 可知：各级导叶上p1位置的压力脉动频域值主要以叶片通过频率为主，且压力脉动主要集中在低频区；首级导叶上p1位置的主频f=243.8 Hz，其他级导叶上p1位置的主频为f=341.32 Hz。

图5 所示为各导叶上p2位置的压力脉动时域图。由图5 可知：此位置的压力脉动时域变化具有明显的周期性。从图5 中压力波动情况可以发现：首级导叶上p12点压力随时间变化梯度最大，幅值达到了最大静压值的7.76%。而第五级导叶内的p52点幅值最小，约为最大静压值的4.43%。

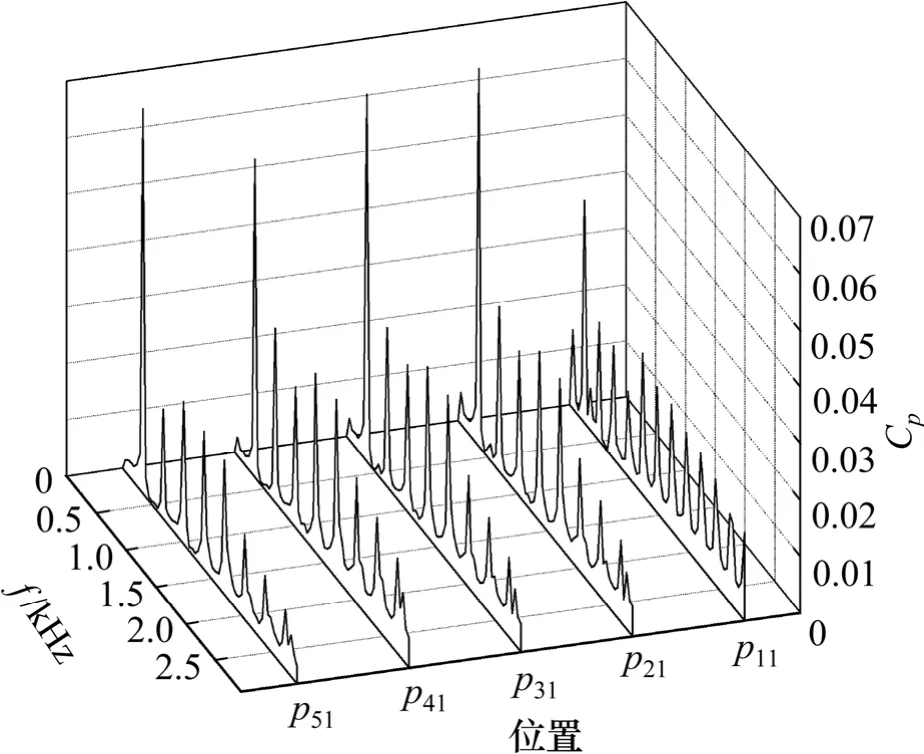
图4 导叶p1 上位置的压力脉动频域图Fig.4 Frequency spectra of pressure fluctuations at p1

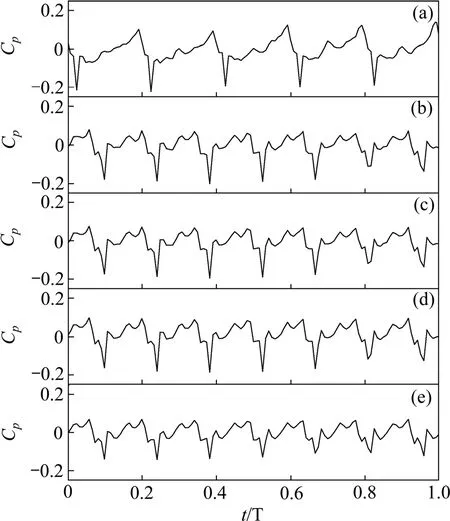
图5 导叶上p2 位置的压力脉动时域图Fig.5 Pressure fluctuations at p2

图6 所示为各级导叶上p2位置的压力脉动频域图。由图6 可知：首级导叶上p2位置的主频f=243.8 Hz，次频f= 487.6 Hz，其他级导叶上p2位置的主频为f=341.32 Hz，显然各级导叶上p2位置的压力脉动的最大幅值都出现在1 倍叶片通过频率处。

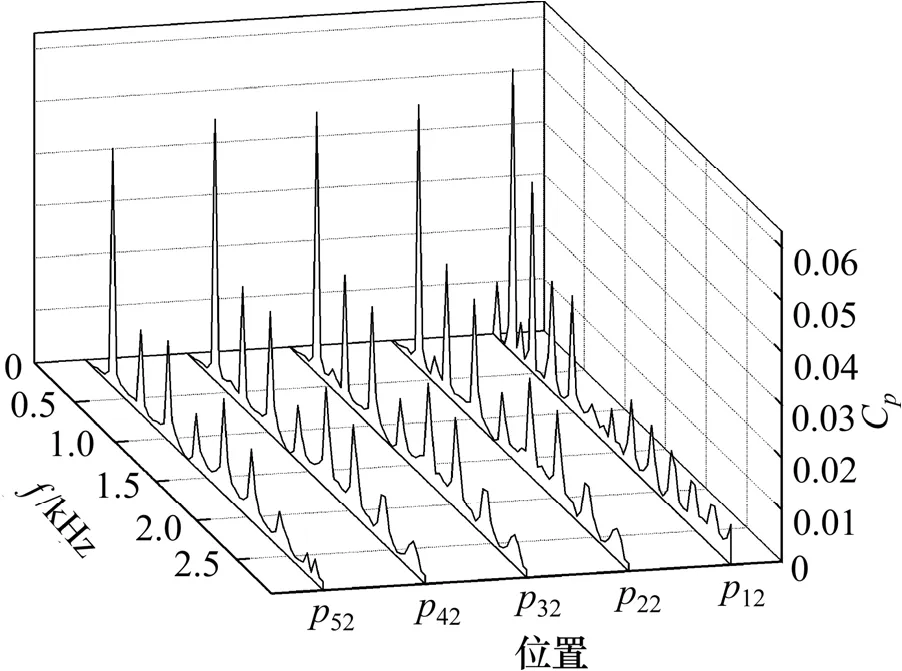
图6 导叶上p2 位置的压力脉动频域图Fig.6 Frequency spectra of pressure fluctuations at p2

图7 所示为各导叶上p3位置的压力脉动时域图。由图7 可知：五级导叶内p3位置的压力脉动都有显著的周期性，与p1和p2相似，叶轮旋转1 个周期内，监测点静压波动p13点出现了5 个小周期，p23，p33，p43和p53出现7 个小周期，各导叶上p3位置的压力变化复杂，在第1 级导叶内的p13点的波动幅值最大。

图7 导叶上p3 位置的压力脉动时域图Fig.7 Pressure fluctuations located at p3

图8 所示为各级导叶上p3位置的压力脉动频域图。由图8 可知：各级导叶上p3位置的压力脉动能量分布相对较均匀，首级导叶存在主频f=243.8 Hz 的脉动，其2，3，4 和5 级导叶主频为341.32，682.65 和1 072.7 Hz。相比p1和p2位置，p3位置脉动幅值相对较低。

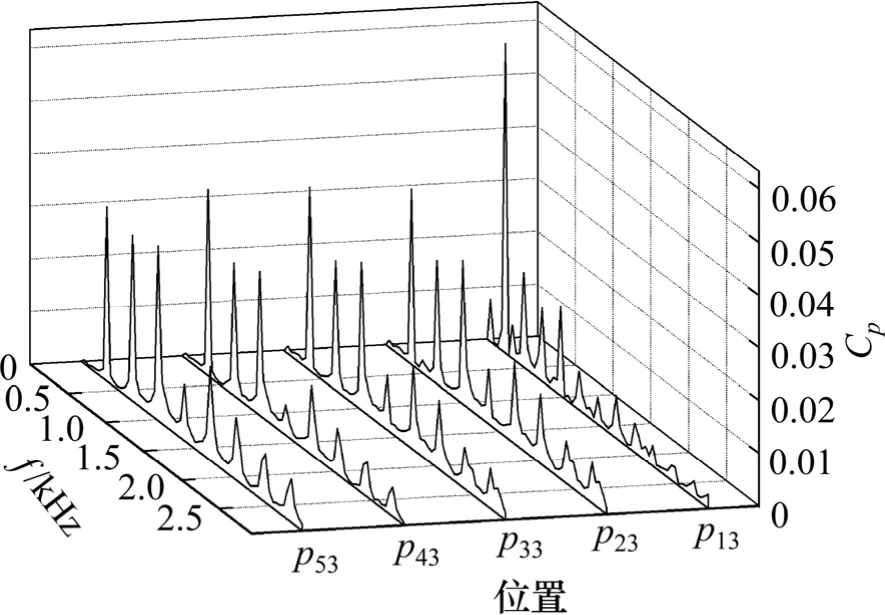
图8 导叶上p3 位置的压力脉动频域图Fig.8 Frequency spectra of pressure fluctuations at p3

与图3 和图4 相比，同一导叶3 个监测点中p1位置的压力脉动最为剧烈，在同一导叶单流道的圆周上，随着离p1位置距离的增大，压力脉动强度逐渐减弱，p3位置的压力脉动的幅值明显减小，同时压力脉动的最大值也显著降低。其原因是：各监测点的压力脉动是因为旋转的叶轮叶片扫过静止的导叶叶片出现叶片尾迹，叶片尾迹引起压力脉动。 尾迹中流体与导叶叶片相互作用影响压力脉动的强弱，在同一导叶内同一圆周上，监测点p1离导叶片进口距离最近，p2和p3点次之。同时，可以发现：无论是压力脉动幅度还是最大压力脉动值，首级导叶内的值都是最大的。

为了进一步分析泵内监测点内的压力脉动情况，对各级导叶内监测点压力脉动幅度CA进行统计，如表4 所示。由表4 可知：最大的波动幅度在泵的第1 级导叶内的p1位置，最高可达到8.25%，在第4 级导叶内的p3位置脉动幅度达到最小值，仅为4.28%。单导叶内0.8D4半径的圆周上的监测点以导叶叶片进口p1为起点，p3为终点，波动幅度变化相一致，且都逐渐降低。而在此五级离心泵内，各导叶内同一位置上监测点的压力幅度变化趋势基本一致，都随泵级数的增加逐渐降低。

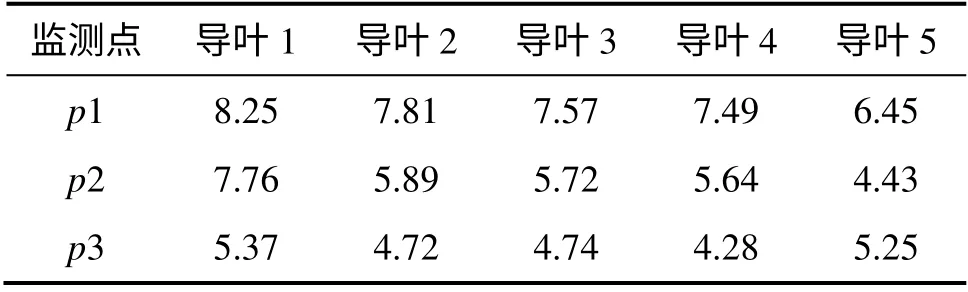
表4 导叶内监测点压力脉动的波动幅度CATable 4 Fluctuation amplitude of monitoring points in diffusers %

3 结论

1) 各级导叶内单流道进口处压力波动具有显著的周期性，且第2，3，4 和5 级压力波动基本同步。

2) 对于五级离心泵单流道进口处压力脉动，第1级的压力脉动最剧烈，且压力脉动随级数的增加逐渐减轻。

3) 各级导叶单流道进口0.8D4半径的圆周上的监测点，p1点位置波动最为剧烈，且在此条件上，离p1位置越近，波动越剧烈。首级导叶p11点的压力波动幅度为8.25%。

4) 叶片压力脉动频率主要以叶轮叶片通过频率为主，且在p1和p2位置的压力脉动的最大幅度出现在1 倍叶频处。

[1] 瞿丽霞, 王福军, 丛国辉, 等. 双吸离心泵叶片区压力脉动特性分析[J]. 农业机械学报, 2011, 42(9): 79-84.QU Lixia, WANG Fujun, CONG Guohui, et al. Pressure fluctuations of the impeller in a double-suction centrifugal pump[J]. Transactions of the Chinese Society for Agricultural Machinery, 2011, 42(9): 79-84.

[2] 袁寿其, 叶丽婷, 张金凤, 等. 分流叶片对离心泵内部非定常流动特性的影响[J]. 排灌机械工程学报, 2012, 30(4): 373-378.YUAN Shouqi, YE Liting, ZHANG Jinfeng, et al. Influence of splitter blades on unsteady flow characteristics in centrifugal pump[J]. Journal of Drainage and Irrigation Machinery Engineering, 2012, 30(4): 373-378.

[3] 朱荣生, 王韬, 付强, 等. 基于CFD 技术的核电站上充泵全流场数值模拟[J]. 排灌机械工程学报, 2012, 30(1): 30-34.ZHU Rongsheng, WANG Tao, FU Qiang, et al. CFD numerical simulation of flow field in charging pump for nuclear power plants[J]. Journal of Drainage and Irrigation Machinery Engineering, 2012, 30(1): 30-34.

[4] 谈明高, 黄道见, 刘厚林, 等. 八级蜗壳式煤制油泵的水力设计[J]. 水泵技术, 2011(3): 14-17.TAN Minggao, HUANG Daojian, LIU Houlin, et al. Design for eight-stage pump with volute used in the technology of getting oil from coal[J]. Pump Technology, 2011(3): 14-17.

[5] 张人会, 郑凯, 杨军虎, 等. 离心泵叶轮的参数化设计[J]. 排灌机械工程学报, 2012, 30(4): 417-421.ZHANG Renhui, ZHENG Kai, YANG Junhu, et al. Parametric design of centrifugal pump impellers[J]. Journal of Drainage and Irrigation Machinery Engineering, 2012, 30(4): 417-421.

[6] 赵运革. 基于数值模拟的多级双吸式离心泵性能预测[J]. 中国农村水利水电, 2012(4): 99-101.ZHAO Yunge. Performance prediction of multi-stage double–suction centrifugal pump based on the numerical simulation[J].China Rural Water and Hydropower, 2012(4): 99-101.

[7] YANG Conxin, CHENG Xiaowei. Numerical simulation of three-dimensional flow in a multistage centrifugal pump based on integral modeling[C]// Proceeding of the Power and Energy Engineering Conference. Wuhan: IEEE, 2009: 1-5.

[8] 蒋庆磊, 翟璐璐, 吴大转, 等. 多级离心泵内叶轮出口压力脉动研究[J]. 工程热物理学报, 2012, 33(4): 599-602.JIANG Qinglei, ZHAI Lulu, WU Dazhuan, et al. Pressure fluctuation at impeller outlet in multistage pump[J]. Journal of Engineering Thermophysics, 2012, 33(4): 599-602.

[9] 孔繁余, 薛玲, 王婷, 等. 复杂泵体压力脉动特性的数值模拟[J]. 华中科技大学学报(自然学版), 2012, 40(8): 12-16.KONG Fangyu, XUE Ling, WANG Ting, et al. Numerical simulation of pressure fluctuations in complex pumps[J]. Journal of Huazhong University of Science and Technology (Nature Science Edition), 2012, 40(8): 12-16.

[10] Yutaka K, Tomoshige T, Sakuichiro U, et al. Prediction of system instability by measuring the dynamic characteristics of prototype multistage centrifugal pump[J]. Technical Review Mitsubishi Heavy Industries, 1988, 25(3): 160-164.

[11] 施卫东, 张磊, 陈斌, 等. 离心泵间隙对压力脉动及径向力的影响[J]. 排灌机械工程学报, 2012, 30(3): 260-264.SHI Weidong, ZHANG Lei, CHEN Bin, et al. Influence of gap on pressure pulsation and radial force of centrifugal pumps[J].Journal of Drainage and Irrigation Machinery Engineering, 2012,30(3): 260-264.

[12] 朱荣生, 李小龙, 袁寿其. 1 000 MW 级核主泵压水室出口压力脉动[J]. 排灌机械工程学报, 2012, 30(4): 395-400.ZHU Rongsheng, LI Xiaolong, YUAN Shouqi, et al. Collector discharge pressure fluctuation of 1000MW nuclear reactor coolant pump[J]. Journal of Drainage and Irrigation Machinery Engineering, 2012, 30(4): 373-377.

[13] 杨帆, 刘超, 汤方平, 等. 灌排双向立式泵装置内部水流压务脉动特性[J]. 排灌机械工程学报, 2012, 29(4): 316-321.YUNG Fan, LIU Chao, TANG Fangping, et al. Analysis on pressure fluctuation of interior flow in reversible pumping system for irrigation and draigage[J]. Journal of Drainage and Irrigation Machinery Engineering, 2012, 29(4): 316-321.

[14] Guelich J, Bolleter U. Pressure pulsations in centrifugal pumps[J]. Journal of Vibration and Acoustics, 1992, 114(2):272-279.