无定向导线在高速铁路水平位移监测中的应用及精度分析

杨忠伍 上海铁路局蚌埠工务段

无定向导线在高速铁路水平位移监测中的应用及精度分析

杨忠伍 上海铁路局蚌埠工务段

高速铁路在施工期间，其路基需要进行水平位移监测。由于高速铁路线路周围控制点的稀少与不通视，常规的监测方法受到了制约，在此条件下可考虑使用无定向导线方法进行监测。通过对所采集的数据进行精读评定与分析，并与相应规范中的精度标准对比，判断无定向导线方法能够在精密变形监测中使用。。

无定向导线；变形监测；精度分析；水平位移

1 引言

高速铁路路基作为变形控制十分严格的土工构筑物,施工中和铺板、铺轨前均应进行水平位移监测,分析其变形监测数据并指导施工。在选择监测方法时，需要考虑监测的环境与具体条件，高速铁路路基监测区域的控制点间距较远且不通视，同时施工路基不断被填压，造成附近地面变形，难以就近加密工作基点，但要求的监测频率较高。综合考虑以上因素，为了保证工作效率，可不采用常规监测方法，改用不加密工作基点的无定向导线方法进行监测。

2 无定向导线的定义

无定向导线是指无法观测方位连接角，而在两已知点间布设的、没有方位起算信息的、特殊形式的附合导线，如图1所示。当A、B两个控制点间无法通视，不能确定导线起始边方位角的情况下，可以利用这两控制点建立一条无定向导线，从而获得起算数据。在一条有n个待定点的无定向导线中，含n+1条观测边和n个观测角，必要观测数是2n个，所以多余观测数只有1个，亦即长度闭合是唯一的的多余观测条件。

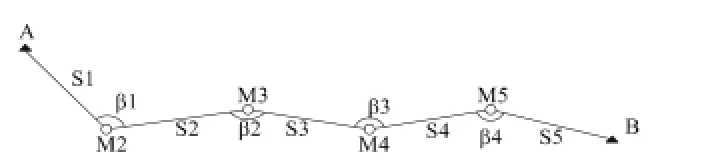
图1 n无定向导线示意图

3 无定向导线的平差解算思路与平差方法

如图1，首先假定该导线的起始边的坐标方位角(一般假定该起始方位角为)，用假定的起始方位角以及各导线点的角度观测值，计算其余导线边的假定方位角，然后结合各导线边的边长观测值，可计算出终点B在假定坐标系中的坐标。无定向导线进行概略坐标计算时，首先确定起算点的坐标，将其与已知点A重合，然后进行旋转，令两个控制点间长度作为导线固定边（如图1中A、B两点连接成的边），将两控制点的已知方位角作为导线的定向标准对导线进行变换，令旋转后的终点坐标与实际坐标相吻合。但是由于观测值中存在误差，所以旋转后终点的坐标值与实际的控制点坐标存在不符值，因此需要运用平差方法进行解算，以达到消除不符值并评定精度的目的。

3.2 平差方法

以A为坐标原点，先假设第一条边的方位角为α（1可以任意取值，可假设，如图1，按导线计算公式：

式中，α1为各条导线的方位角；βi为各导线点的角度观测值；xi，yi为导线点计算过程中的坐标值；xi+1，yi+1为下一个导线点的坐标值；Si为各导线边的距离观测值。

当i=5时，由式(1)可求得B的假设坐标x'B=x6，y'B=y6。由下式可以计算出A和B两点在假定坐标系中的方位角α'AB。

2.2.2 腹痛程度 疗后第2周，两组腹痛程度的改善率，差异有统计学意义，试验组优于对照组，FAS、PPS分析结论一致。FAS数据集结果见表4。

然后按照间接平差方法进行平差，步骤如下：

（1）利用控制点的坐标，测量所得的各导线边长和反算出的坐标方位角，计算各导线点坐标的近似值x0i、y0i。选近似坐标x0i、y0i的改正数作为未知参数。

（2）将每一个观测量的平差值分别表达成所选参数的函数，若函数非线性，则要将其线性化，然后列出以未知参数表示的边长改正数Vsi、角度改正数Vβi的误差方程。

每条观测的导线边都可开列一个如下形式的边长误差方程：

每两条导线之间观测的夹角都可开列一个如下形式的角度误差方程：

式中，ΔX0和ΔY0分别为坐标变化量的概略值，和分别为坐标改正数，S0为近似边长，v是观测值改正数，l为常数项，ρ=206265″。

（3）由误差方程的系数矩阵B和常数项l组成法方程，法方程阶数等于未知参数的个数。

（4）用δx表达坐标改正数矩阵，则，用该公式求出坐标改正数；，再用该公式求出观测值改正数；，然后用该公式求出方差再计算出参数的平差值。

4 无定向导线的精度分析与计算实例

4.1 精度分析

常规的附合导线有3个多余观测数，而无定向导线只有1个多余观测数，检核条件较少，因此可能会对无定向导线的精度产生顾虑。在控制点间距固定的前提下，一条导线的精度在一定程度上可用该导线的最弱点点位中误差来判断。由相关资料可知无定向导线最弱点点位中误差的计算公式：（5）

式中，m为最弱点点位中误差(mm)；n为导线边数；mβ为测角中误差(″)；mS为边长中误差(mm)；S为导线的平均边长(mm)。

在高速铁路路基水平位移变形监测中，导线长度一般为1km，平均边长250m，使用型号为TCA2003的全站仪进行观测，标称精度测角为0.5″，测距为1mm+1ppm。仪器的标称精度是一种误差限差的概念，仪器的实际测量误差接近该限差，也可能小于或远小于该限差。现用以上标称精度作为导线的测量精度代入（5）式，比较导线边数的变化对无定向导线最弱点点位中误差的影响，见表1。

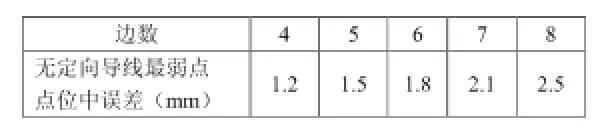
表1 边数对无定向导线最弱点点位中误差的影响

从表1可以看出，在其他条件不变的情况下，导线最弱点点位中误差与导线总长度成正比。还可看出，随边数的增加，无定向导线最弱点点位中误差也会逐渐增大。因此合理的导线布设能较好的保证无定向导线的精度。

4.2 计算实例

将测量所得数据按照上述模型进行平差计算后，统计使用无定向导线方法监测的最弱点精度，列于表2。

表2 无定向导线方法监测的最弱点精度统计

按照误差传播定律，可推导出两周期监测点的位移量中误差计算公式：

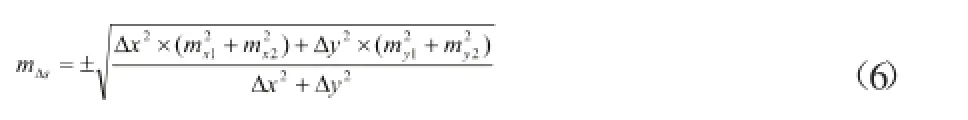
式中，mΔs为监测点的位移量中误差；ΔX、ΔY分别为两周期观测中该点在X、Y方向的位移量；mx1、mx2和my1、my2分别为在第一、二周期观测中该点X和Y方向的中误差。

根据（6）式，代入使用无定向导线方法测量的具体数值，将结果列于表3。

表3无定向导线监测点的位移量中误差统计表

从《工程测量规范》GB50026-2007中可得知一、二等水平位移监测网的精度要求，见表4。将表2、表3与《工程测量规范》中对水平位移监测的相应要求作比较。

表4 一、二等水平位移监测网精度要求[8]

从以上表格中的数据比较可以看出，由TCA2003全站仪采用无定向导线方法测量所得的数据，经过分析，判断所采集数据能达到的变形监测精度介于一等和二等之间，可满足二等变形监测精度的要求，证实了无定向导线可以在精密变形监测中应用的可行性。

5 结论

（1）在高级控制点稀少或控制点之间通视条件差，导线两端的定向角难以测定的情况下，可以采用无定向导线。

（2）由于高精度智能全站仪的出现，使无定向导线的测量精度得到大大提高，并且测量方法灵活，不要求控制点间通视，工作效率高，使得在精密变形监测中应用无定向导线方法具有可行性。

（3）由于无定向导线没有方位角闭合条件，因此采取措施提高测角精度、采用严密的平差方法对其进行平差，可以弥补高级控制点数量不足的缺陷，从而达到对工程实施有效控制的目的。

责任编辑：宋飞 龚佩毅
来稿时间：2014-11-13