混合编程技术在车辆部件故障统计分析中的应用

唐继烈 上海铁路局科研所

混合编程技术在车辆部件故障统计分析中的应用

唐继烈 上海铁路局科研所

阐述如何运用可靠性统计原理建立故障样本统计数学模型，充分发挥C#和MATLAB两种编程语言各自在可视化界面和数学计算的优势，通过将二者混合编程计算出的车辆部件可靠性威布尔分布的估计参数值，根据对车辆轴箱弹簧故障实例的计算，得出其平均无故障走行里程和可靠度曲线。为车辆的运用和检修提供参考。

混合编程；车辆故障；统计分析

随着当前铁路高速、重载的发展，对车辆部件的可靠性要求越来越高。常用的研究手段是运用可靠性统计原理建立故障样本统计数学模型。车辆故障的统计分析是根据故障模式、故障机理、故障的影响及其后果的严重程度，分析车辆部件的失效规律，估计部件的可靠度或故障间隔里程(MDBF)，以便采取措施预防故障的发生，提高车辆运行的可靠性，可为车辆的运用和检修计划优化提供参考依据。

运用统计学定量分析方法建立故障样本的威布尔分布数学模型，计算分布参数估计值需要求解超限方程，求解过程较复杂。本文提出利用C#编程语言在可视化界面设计和数据库操作的优势，利用MATLAB在复杂数学计算领域的优势，通过C#和MATLAB混合编程技术求解参数的估计值。最后计算出车辆轴箱弹簧平均无故障走行里程和可靠度曲线。

1 可靠性统计分析理论方法

可靠性统计分析的一般步骤是对研究对象的失效机理做物理分析并结合以前的经验，提出该批统计数据的假设分布，对假设分布做参数估计，求出可靠度函数，进一步计算可靠度、平均故障间隔时间等一系列指标。其中最重要的工作是分布的假设和参数估计。

车辆故障的规律和性质随着发生故障的部位变化而变化，不同的故障部位所发生的故障应用不同的数学模型来建模和描述。根据参考文献，在可靠性工程中常用的分布主要有对数正态分布、指数分布和威布尔分布。对数正态分布应用范围主要是寿命现象事件在端部时的不对称情况，且观测值的离散度很大，例如：电机绕组绝缘，风扇叶片，车体结构等部件。指数分布应用范围主要是系统、部件的寿命，适用于偶然失效与使用时间无关的元件，例如：电子设备和电子元件，多个不就组成的复杂系统，某些软件的故障模型等。威布尔分布应用范围主要是有薄弱环节的模型，机械中的疲劳强度，磨损寿命，腐蚀寿命等，例如：滚动轴承，传动齿轮箱，继电器等零部件。

威布尔分布是可靠性定量分析中常用的一类寿命分布，在可靠性工程中有着非常广泛的应用。在此仅讨论在车辆部件使用较多的威布尔分布定数截尾情形下可靠性统计分析。分布的参数估计也有多种方法，如图估计法、最小二乘估计法、矩估计法和极大似然参数估计法。其中极大似然估计法的估计量有很好的性质，如具有唯一性和最小方差性，当n→∞时，其渐近状态具有最优性、正态性和有效性。本文计算选择极大似然参数估计法。

车辆零部件的故障数据一般来自现场，样本数量较大，适合采用极大似然法进行参数估计，下面介绍两参数威布尔分布的极大似然参数估计，根据参数估计值就可以计算出部件的平均无故障运行里程和可靠性曲线。

两参数威布尔分布的可靠度函数为

两参数威布尔分布的密度函数为：

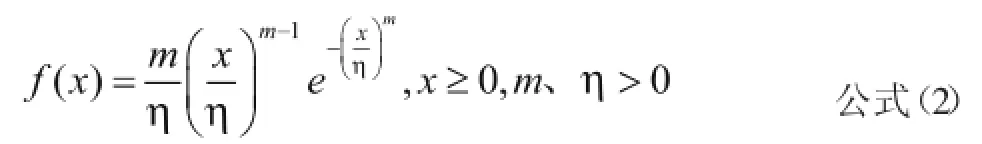
其中：η-尺度参数也称特征寿命，是一种寿命均值并给出分布中点的大致位置，m-形状参数，其大小决定密度曲线的形状。

对n个部件进行可靠性寿命试验直到r个部件失效为止，即定数截尾情形下，得到部件失效时走行的里程的顺序统计量为x1≤x2≤…≤xr。其中：r为失效部件个数，n为样本总数，包括截尾(失效)和未截尾（未失效）的，xi为第i个部件失效时走行里程数，x0为截尾走行里程数（统计截止时未失效部件的走行里程数）。

威布尔分布定数截尾情形下极大似然估计方程为：

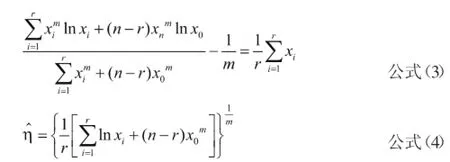
分布的参数估计值求解的实质就是已知参数xi、r、n求解参数估计值m、η。由于公式（3）是超越方程，解析解不易球场，一般只能求出数值解，可借助于专业的数学软件MATLAB来用迭代法计算。后面详述C#和MATLAB混合编程求解过程。

部件的平均无故障运行里程，计算公式为：

其中Γ为伽玛函数，在MATLAB软件中有对应的gamma函数，平均无故障运行里程直接带入参数m、η计算得到。

2 C#和MATLAB混合编程

MATLAB是由美国MathWorks公司开发的数学软件，用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境。同时在众多的附加工具箱(Toolbox)支撑下，被广泛用于控制系统设计与分析、图像处理、信号处理、系统模拟等方面，其m代码简单易学、执行效率高，是进行算法设计与验证的常用工具，MATLAB利用自带的deploytool可以将m代码转换为DLL库。但是MATLAB对于界面开发存在源代码不易封装，可移植性较差。

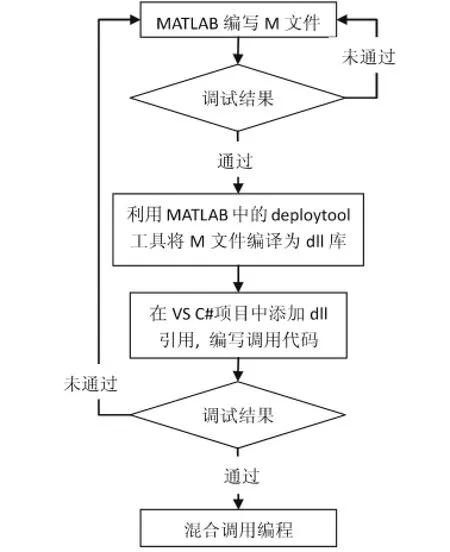
图1 C#与MATLAB混合编程主要实现过程

C#是微软公司推出的一种基于.NET框架的高级编程语言，目前被广泛使用。把上述C#和MATLAB两种编程语言的优点集中起来，在故障统计分析中发挥其优势。通过在C#开发环境下调用MATLAB中生成的DLL库，使得在MATLAB中设计的算法可以直接变为C#程序的一部分，使用时也不需要安装MATLAB软件，方便软件使用者。由C#语言编写程序前台界面、数据库的查询、输入编辑，由MATLAB语言生成负责算法的DLL库在后台完成复杂计算工作，再把计算结果返回给C#程序，由C#实现结果可视化。混合编程主要实现过程如图1所示。

在MATLAB2012a中建立M文件，根据式(3)、(4)、(5)求解求解参数估计值m、η和平均无故障走行里程MDBF，编写MATLAB程序代码，通过deploytool工具将M文件编译成DLL文件。ParaEstCal()为调用函数，M文件主要代码如下：

在VisualStutio2010中新建VisualC#的Windows应用程序，添加MATLAB编译的DLL引用，并添加从MATLAB安装目录名为dotnetbuilder文件夹下拷贝出MWArray.dll文件。同时添加如下命名空间：usingMathWorks.MATLAB.NET.Arrays；usingMathWorks.MATLAB.NET.Utility；

C#初始化调用MATLAB的环境。C#通过故障数据库查询出故障截尾走行里程、总样本数、截尾里程，将以上三个参数转换为MWArray；调用DLL中估计参数计算函数ParaEst－Cal()；返回分布参数η、分布参数m、平均无故障走行里程；C#通过将参数m、η带入公式(1)即可绘制出可靠度曲线。

3 应用实例

以轴箱弹簧断裂故障为例，其可靠性符合威布尔分布。选取样本共计n=3584个，截尾寿命（未失效）为223.4万km，其中轴箱弹簧故障共计r=12个,故障时走行里程xi分别为(单位：万km)：83，70，108，126，148，151，195，204，199，206，183，198。通过C#和MATLAB混合编程求解得出m=3.27，η= 0.8966，单个轴箱弹簧平均无故障走行里程为MDTF=1023（万km），车辆轴箱弹簧可靠度曲线如图2所示。

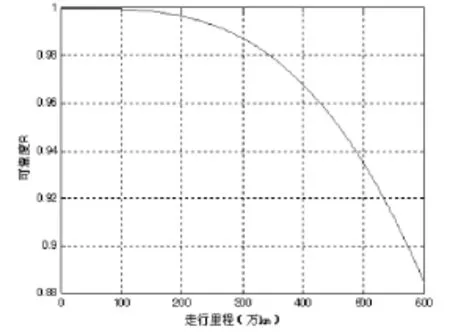
图2 车辆轴箱可靠度曲线

120万km对应的可靠度为0.9994，240万km对应的可靠度为0.9939。16辆车编组形式单列车轴箱弹簧为128个相同轴箱弹簧，这128个轴箱弹簧组成串联模型，16辆车编组形式单列车轴箱弹簧的平均无故障走行里程为：

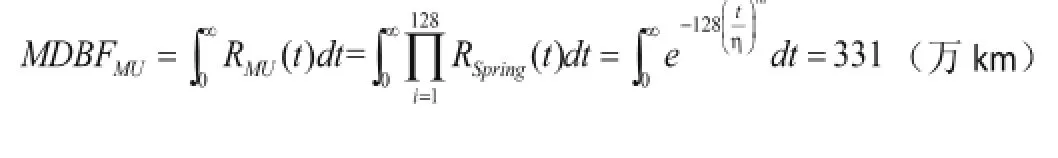
4 总结

本文通过C#和MATLAB混合编程实现部件可靠度分布估计参数值的计算，并以曲线图表的形式显示。充分发挥了MATLAB在复杂数学计算的优势，C#可视化界面编程和数据库访问的优势，通过混合编程降低了软件编程求解估计参数值的数学计算难度，缩短了开发周期，混合编程技术将可靠性统计理论应用于车辆部件故障统计分析的工程实践。

[1]董锡明.机车车辆运用可靠性工程[M].北京：中国铁道出版社，2005.

[2]王远翔，贾志凯，张惟皎.动车组故障统计与配件寿命分析[J].铁路计算机应用，2013，22（1）：29-32.

[3]陈欣.运用可靠性统计原理进行活塞寿命分析[J].铁道技术监督，2006，34(8):9-11.

[4]盛骤，谢式千，潘承毅.概率论与数理统计[M].北京：高等教育出版社，2010.

[5]贺超英.MATLAB应用与实验教程[M].北京：电子工业出版社，2010.

责任编辑：王华张建强来稿日期：2014-10-30