利用VLBI和超导重力资料研究自由核章动周期时变特征

崔小明，孙和平，徐建桥，周江存，周红伟

1中国科学院测量与地球物理研究所 大地测量与地球动力学国家重点实验室，武汉 430077

2中国科学院大学，北京 100049

3厦门地震勘测研究中心，厦门 361021

1 引言

自由核章动（FCN，Free Core Nutation）是旋转椭球型地球的固体地幔与液态外核间相互作用而产生的逆向本征模，在地球参考系中称为近周日自由摆动（NDFW，Nearly Diurnal Free Wobble）（徐建桥等，1999）.

FCN现象在重力信号中的振幅非常小，低于目前观测精度最高的超导重力仪的观测精度，因此在重力资料中难以直接观测到；而FCN是VLBI观测的天极偏差的主要成分，振幅大约为几百微角秒左右，但信号表现出非常大的时间变化特性还存在疑问（Vondrák et al.，2005）.FCN现象在天球坐标系中的章动观测和地球坐标系中的固体潮观测中，可以分别引起与其频率相近项出现共振放大现象，根据VLBI章动观测资料和超导重力资料可以研究自由核章动的本征周期和品质因子等共振参数.之前许多学者利用VLBI和重力资料对FCN进行了研究（Defraigne et al.，1994；Ducarme et al.，2009；

Herring et al.，1986；Koot et al.，2008；Lambert and Dehant，2007；Rosat and Lambert，2009），不同观测资料及方法得出的FCN本征周期结果基本在430天左右，观测资料的积累也为研究FCN周期是否具有周期性的时间变化问题提供了基础，不同的研究结果之间还存在较大的争议（Hinderer et al.，2000；Xu and Sun，2009；Roosbeek et al.，1999；Vondrak and Ron，2009），由于FCN的共振参数反映了地球内部尤其是核幔边界的物理性质及耦合特征，因此这些参数的变化及其影响机制的研究对于更好地认识地球深内部具有重要的意义.

本文针对上述问题，选取6个VLBI天极偏差序列和全球超导重力仪网络中7个精度较高的欧洲台站的重力观测资料拟合地球自由核章动共振参数，旨在研究FCN本征周期的时间变化特征，并通过考虑了核幔边界黏滞和电磁等耗散耦合的FCN的理论模型分析影响FCN本征周期的主要因素，以对其时变性机制进行探讨.

2 资料

本文使用由下列机构解算的天极偏差序列（Celestial Pole Offset）：BKG（Bundesamt für Kartographie und Geodäsie，Germany），GSF（NASA／Goddard Space Flight Center），IVS（the International VLBI Service for Geodesy and Astrometry），OPA（the Paris Observatory IVS Analysis Center），IAA（Institute of Applied Astronomy，St.Petersburg）和USNO（U.S.Naval Observatory）.除IVS为多个序列的综合解外，其他天极偏差序列均由OCCAM或CALC／SOLVE软件解算，给出的序列除IAA外均为天球中间极（CIP）坐标的改正dX和dY，IAA序列为黄经章动和交角章动的天极偏差观测值dψ和dε.偏差对应的章动岁差模型为IAU2000A／IAU2006，其中的章动模型均为MHB2000，序列的时间跨度为（1984—2010－11）.重力观测资料是由全球地球动力学合作观测与研究计划（GGP）下的超导重力仪网络提供，该计划始于1997年，GGP组织规定使用统一的GWR超导重力仪，安装统一的数据采集设备，使用统一的中央传感器、低通滤波器和相同的国际标准数据处理方法处理观测数据.本项研究中使用了欧洲Strasbourg，Vienna，Wettzell，Medicina，Membach，Metsahovi，Moxa等7个台站的超导重力仪高精度和高密度采样数据，观测区间为十年到十五年不等.所用VLBI和超导重力数据详细信息见表1和表2.

表1 所用VLBI数据的基本信息Table 1 Information of VLBI data used in this paper

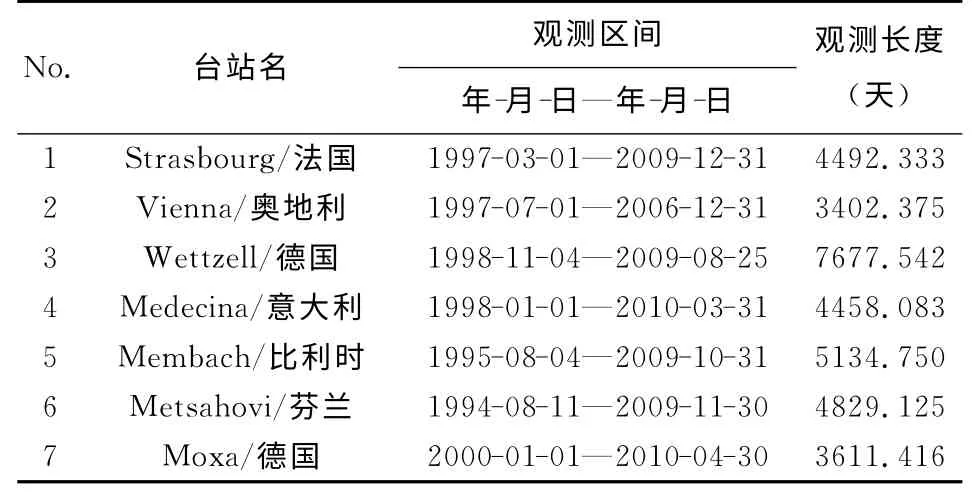
表2 所用超导重力数据的基本信息Table 2 Information of SG data used in this paper

3 FCN本征周期

3.1 VLBI资料拟合FCN本征周期

FCN本征周期的拟合是基于在VLBI章动观测和SG重力观测中与其频率相近的章动项或固体潮潮波产生的共振现象.章动观测的共振公式采用Mathews等（2002）公式（42）：

其中，eR＝（C－A）／A是刚性地球动力学椭率，eR＝0.0032845075；σ为地球参考系中频率（terrestrial frequency），单位为cpsd（cycles per sidereal day）；s1，s2，s3和s4分别为钱德勒摆动（CW），自由核章动（RFCN），内核自由章动（PFCN／FICN）和内核自由摆动（ICW）的频率.Mathews等（2002）中表6给出了这四个频率以及N0，Q0，Q1，Q2，Q3和Q4等共振参数的参考值.以s2和Q2为未知数，利用最小二乘法即可拟合FCN本征周期等参数.

共振公式的观测值T（σ）＝η（σ）／ηR（σ），其中η（σ）为非刚性地球章动振幅，ηR（σ）为刚性地球章动振幅，本文采用Souchay等（1999）的刚性地球章动模型给出的ηR（σ）.η（σ）的计算首先要利用VLBI天极偏差序列解算章动项改正系数.

章动项改正系数的解算采用Herring等（1986）的计算模型（张捍卫和覃伯平，1995）：

其中，δψrj，δψij和δεrj，δεij分别为幅角为θj的黄经章动项和交角章动项系数改正的实部和虚部；Cψ和Cε是相对于历元J2000的章动角的常数改正；和是线性速率项，t为相对于J2000的儒略世纪数.δΔψ（t）和δΔε（t）为天极偏差观测值，目前大多数机构解算的天极偏差序列都是相对于IAU2000A岁差章动模型的天球中间极（CIP）坐标的改正dX和dY.dX≈δΔψ（t）·sinε0；dY≈δΔε（t）（1980—2020时段 内 误 差 小 于1微 角 秒）；ε0＝84381.406″，为J2000.0历元的平黄赤交角（IERS Conventions，2010）.

本文选取365.26天（l′），182.62天（2F－2D＋2Ω），121.75天（l′＋2F－2D＋2Ω），27.55天（l）和13.66天（2F＋2Ω）等5个主要章动项来解算章动改正系数，同时拟合周期为460天的FCN项（幅角为fFCN·t，fFCN为FCN角频率），在主要章动项改正系数的解算中移除18.6年（Ω）和9.3年（2Ω）两个长周期项以及常数改正项和线性速率项.

每个章动项在天球坐标系下都是一个椭圆运动，可以表示为两个关于恒星频率对称的圆章动的叠加.根据公式（2）和（3）及加权最小二乘法拟合的章动项改正系数经Herring等（1986）公式（5）—（6）计算相应圆章动项的改正系数，最后根据MHB2000章动模型计算非刚性地球章动振幅η（σ）.

利用2节中所述BKG，GSF，IAA，IVS，OPA和USNO等6个不同机构解算的天极偏差序列，选取观测精度较高的1990年之后的观测值，截至时间为2010或2011年.以6年滑动时间长度，5年重叠率，根据上述方法分段拟合FCN共振参数，结果列于图1中，从图中可以看出，不同机构解算的天极偏差序列拟合的FCN本征周期结果之间比较一致，变化幅度小于1天，且存在十年尺度的时间变化特征.

图1 不同序列解算的章动改正系数拟合的FCN共振周期Fig.1 FCN period calculated from different celestial pole offsets

3.2 超导重力资料拟合FCN共振周期

重力观测中由于NDFW（即FCN在地固系中的表现形式）导致某些周日潮波观测中出现较大的共振放大现象.周日频段内随频率σ变化的重力振幅因子共振公式为（徐建桥等，1999）：

根据公式（5），选取经Fes04海潮模型计算的海潮负荷改正的P1，K1，Ψ1和Ф1等4个潮波的重力振幅因子，利用加权最小二乘法和超导重力观测资料即可拟合得到NDFW的共振强度和本征频率，之后FCN的品质因子（Q值）和共振周期可由（6）式计算：

其中，Ω为地球自转角速度，单位为（°）／h.

考虑到GGP欧洲台站的观测比较稳定，受海潮影响较小，观测资料质量高，本文采用7个欧洲台站的超导重力仪时变重力观测资料.这些资料都已利用国际地球潮汐中心推荐的T－soft软件（Vauterin，1998），修正了其中的阶跃、尖峰、掉格和地震等干扰信号.再对重力和辅助气压数据进行滤波和重采样处理.我们将7个台站的数据以3年滑动时间窗口（2.5年重叠，因重力资料相对VLBI资料长度较短）分段，并采用统一分析软件（Eterna）调和分析各台站不同时段的重力潮汐观测数据，获得重力因子、相位滞后等潮汐参数.之后利用上述方法拟合FCN的本征周期等参数，结果及其多项式拟合曲线列于图2中.

从拟合结果来看，单个台站数据获得的FCN本征周期离散度较大，仅能看出部分台站在相同时段有近似的趋势，但并不明显.对比超导重力资料和VLBI获得的共振结果，由于与FCN本征频率接近的主要共振章动项的振幅较大，因而用VLBI资料拟合的章动系数具有较高的精度，由此拟合的FCN参数变化幅度较小；而重力观测中，与FCN有关的周日共振潮波中Ψ1和Ф1的振幅较小，调和分析得到的相应结果精度较低，造成重力观测资料拟合的FCN参数变化幅度较大.为获得精度更好的结果，我们采用相同时段多台站数据迭积的方法.迭积的实质是加权最小二乘法（Defraigne et al.，1994；Ducarme et al.，2009），即综合多台站观测联合平差解算FCN参数，尽可能地利用全球多台站观测的优势，仍然采用3年滑动时间长度，由于各个台站的观测数据时段并不完全相同，每个迭积时段包括4～7个台站的数据.FCN本征周期的迭积拟合结果如图3所示.迭积后的结果明显离散度变小，表明多台站迭积结果可以明显地弥补部分潮波观测精度不足的缺陷.图3中的FCN周期时变特征与VLBI结果相比，虽然变化幅度稍稍偏大，但是大致的变化趋势相同，仅2000年左右的几个结果偏离.

根据3.1和3.2节的结果，利用VLBI和超导重力资料获得的FCN周期表现出相似的时变性，存在十年尺度的时间变化特征.目前对于FCN时变性问题的研究还存在比较大的争议，Hinderer等（2000）利用重力和VLBI资料进行了研究，但由于观测资料较短，获得的结果不足以反映出FCN的时变特征；Vondrak和Ron（2009）等利用VLBI资料探讨了该问题，获得的FCN周期结果存在一定变化特征，鉴于变化的幅度较小，认为FCN周期是稳定的；Xu和Sun（2009）利用布鲁塞尔台站1982—2000年的超导重力观测资料的研究结果显示FCN周期存在十年尺度的变化特征.考虑到FCN周期的变化幅度较小，因此利用VLBI和重力两种观测手段的长期资料对比研究FCN时变性获得的结果相对更具有借鉴意义.

4 FCN周期时变性影响因素

根据角动量平衡方程，考虑核幔边界的耗散耦合，建立刘维尔方程，理论推导的FCN在地固坐标系下的表现形式近周日自由摆动（NDFW）的本征频率为：

其中，Ω为地球自转角速度，A为地球惯量矩，Am为地幔惯量矩，ec为核幔边界动力学椭率，q0＝Ω2ac／g（a），ac为液核半径，g（a）为地球表面重力加速度，为勒夫数，ReKCMB和ImKCMB分别是耦合常数KCMB的实部和虚部.耦合常数代表核幔边界耗散耦合，核幔耗散耦合是FCN现象能量耗散的重要阻尼源，我们采用Mathews和Guo（2005）建立的黏滞耦合和电磁耦合模型（vis表示黏滞，em表示电磁）：

图2 欧洲7个台站超导重力资料拟合的FCN共振周期Fig.2 FCN period calculated from observations at 7Europe stations

图3 欧洲7个台站超导重力资料分段迭积拟合的FCN本征周期Fig.3 FCN periods calculated by stacking observations from 7stations

其中，ρ为液核顶部边界层密度，ν为边界层黏滞系数，μ为真空磁导率，Δ~ω为角动量变化，Af为液核惯量矩，θ为余纬，Iem和Ivis具体表达形式参见Mathews和Guo（2005）.

根据FCN周期的计算公式（6）和（7）可知，决定FCN周期的NDFW本征频率的实部中，ec，~hc1和ReKCMB是影响FCN周期的主要可能变化因素，其中液核动力学椭率是影响FCN周期的最主要因素，而液核的动力学椭率应该是比较稳定的物理参数，因此不会对FCN产生周期性的时变影响，目前对于该参数的异议主要用于解释基于流体静力平衡假设下的地球模型理论模拟的FCN本征周期与实际观测资料分析获得的FCN本征周期之间30恒星日左右的偏差，相关研究将该偏差解释为液核的真实动力学椭率比流体静力学平衡假设下的动力学椭率约大5%～6%（徐建桥等，1999）.对于表征地球形变的勒夫数~hc1，由于目前重力潮汐观测结果和潮汐理论模型非常吻合，所以现有地球形变理论模型可以很好地近似地球的真实形变，而地幔形变参数的微小变化对FCN本征周期的影响非常小（徐建桥等，1999）.对于耗散耦合（耦合常数实部ReKCMB），我们根据公式（7）—（10）计算了电磁和黏滞耦合对于FCN本征周期产生的影响，耗散耦合在相关参数达到一定条件下可以对FCN本征周期产生几个恒星日的影响，其中电磁耦合取决于地幔底部电导率和核幔边界磁感应强度径向分量，而黏滞耦合取决于液核顶部黏滞系数.图4中列出了以上几个决定核幔边界耗散耦合的参数与耦合常数实部ReKCMB的关系.

图4 核幔边界参数与耦合常数实部的关系（（a）黏滞系数；（b）磁感应强度）Fig.4 Relation between CMB parameters and coupling constants（（a）Viscosity；（b）Magnetic field）

图5 1990—2011日长变化时频分析（（a）Wavelet；（b）FFT）Fig.5 Time－frequency analysis of change of LOD from 1990to 2011（（a）Wavelet；（b）FFT）

图中（a）为黏滞系数与ReKCMB的关系，（b）为磁感应强度与ReKCMB的关系，虚线部分为FCN周期变化一天对应的ReKCMB变化量，（b）图中不同颜色曲线代表不同地幔底部电导率情形.从图4中可以看出黏滞和电磁耦合对FCN周期所能产生的影响及需要的参数条件，其中黏滞系数要达到3×103Pa·s，磁感应强度径向分量需大于0.3mT且地幔底部电导率达到5×105S／m.然而对于FCN周期时变性的研究，由于黏滞系数和电导率作为核幔边界物质的物理性质应该比较稳定，尤其是产生周期性的变化并不合理，因此对于存在周期性变化特征的FCN本征周期变化来说，只有核幔边界磁感应强度（只考虑径向分量）可能会由于地球深内部的运动产生时变性，进而引起的电磁耦合变化可以提供较为合理的解释.

核幔边界磁感应强度的径向分量Br由偶极子（dipole）和 非 偶 极 子（non－dipole）磁 场 部 分 组 成（Mathews and Guo，2005），对核幔边界磁感应强度来说，其长波部分（球谐阶数小于等于13）可以由地表观测较好地确定，由此估算的相应核幔边界轴向偶极场强度约为0.209～0.216mT（Langel and Estes，1982；Olsen et al.，2009）；而非偶极子对应的短波部分由于地壳磁场的屏蔽作用而无法从地表观测中获得，因此核幔边界的非偶极场部分是未知的，存在较大的不确定性，这为进一步验证核幔边界磁感应强度的变化引起FCN时变周期造成了障碍.因此我们从另一角度探讨该问题，核幔边界的电磁耦合最早是出于解释十年尺度的日长变化提出的，许多研究也论证了二者之间的相关性（康国发等，2008；Holme and Viron，2005），本文利用国际地球自转和参考系服务（IERS）提供的地球自转参数资料（finals2000A.all，采样间隔为1天）进一步探讨1990—2011年间日长变化与FCN周期变化之间的关系.图5列出了日长变化资料的时频分析结果，从小波分析和傅里叶变换的结果可以明显地分辨各周期分量，其中主要的长周期部分集中在周期约22年分量左右，由于观测资料时间跨度对于十年尺度长周期信号的研究仍然较短，因此可靠性相对较低（参考（a）图小波分析95%置信区间弧线）.为更好地分析日长变化中十年左右周期部分，首先采用巴特沃斯低通滤波器滤掉周年以下的高频信号，然后采用最小二乘拟合方法（郭金运和韩延本，2008）扣除滤波后残差中剩余的除十年左右信号外的其他信号成分（主要为22年项以及其他年际信号），最后的残差结果列于图6中.对比图6与前面图1中给出的同时期FCN周期变化发现，二者具有相似的变化趋势，但存在约1～2年的相位偏移，这也间接地证明了FCN周期变化与电磁耦合的相关性.

那么这种相关性是否反映了二者直接的相互影响关系，或者二者都同源于其他的物理过程，从图4中来看，如果核幔边界磁感应强度径向分量变化导致的电磁耦合的变化造成了FCN周期的时变性，那么首先需要地幔底部存在高导电层（达到液核电导率水平5×105S／m），并且磁感应强度径向分量需要产生较大的变化；对于二者同源性的解释，由于核幔边界非偶极子磁场的磁感应强度与核幔边界流体运动等物理过程有关（康国发等，2008），所以也可能FCN周期变化与磁感应强度一样同源于核幔边界的物理过程.

图6 1990—2011日长变化残差信号Fig.6 Residual of LOD variation from 1990to 2011

5 结论

本文选取6个VLBI天极偏差序列和全球超导重力仪网络中7个精度较高的欧洲台站的重力观测资料拟合地球自由核章动本征周期.VLBI资料拟合的FCN本征周期具有较高的稳定性，变化幅度在1天之内；单个重力观测台站资料拟合的FCN参数缺乏稳定性，多台站资料的迭积结果可以明显地弥补该缺陷，获得的FCN本征周期变化幅度为几天，VLBI和重力观测资料获得的FCN周期表现出相似的时变性，存在十年尺度的时间变化特征.结合核幔边界黏滞电磁耦合，根据FCN的理论模型探讨了影响FCN周期的影响因素，结果表明FCN周期变化与电磁耦合存在相关性，核幔边界磁感应强度径向分量变化导致的电磁耦合的变化可能是造成FCN周期时变性的原因，但需要地幔底部存在高导电层，并且磁感应强度径向分量需要产生较大的变化.

致谢 感谢比利时皇家天文台Ducarme教授提供的超导重力数据；感谢斯特拉斯堡地球物理所Hinderer教授和Rosat教授对文中内容提出的建议.

Defraigne P，Dehant V，Hinderer J.1994.Stacking gravity tides measurements and nutation observations in order to determine the complex eigenfrequency of the nearly diurnal free wobble.J.Geophys.Res.，99（B5）：9203－9213.

Ducarme B，Rosat S，Vandercoilden L，et al.2009.European tidal gravity observations：Comparison with Earth Tides models and estimation of the Free Core Nutation（FCN）parameters／／Sideris M G ed.Proceedings of the 2007IAG General Assembly，July 2－13，Perugia，Italy.Observing Our Changing Earth.Germany：Springer Verlag，IAG Symposia 133：523－532.

Guo J Y，Han Y B.2009.Seasonal and inter－annual variations of length of day and polar motion observed by SLR in 1993—2006.ChineseScienceBulletin，54（1）：46－52.

Herring T A，Gwinn C R，Shapiro I I.1986.Geodesy by radio interferometry：studies of the forced nutations of the Earth 1.Data analysis.J.Geophys.Res.，91：4745－4754.

Hinderer J，Boy J P，Gegout P，et al.2000.Are the free core nutation parameters variable in time？Phys.EarthPlanet Inter.，117（1－4）：37－49.

Holme R，de Viron O.2005.Geomagnetic jerks and a highresolution length－of－day profile for core studies.Geophys.J.Int.，160（2）：435－439.

Petit G，Luzum B eds.2010.IERS Conventions（2010）.IERS Technical Note 36，Verlag des Bundesamts für Kartographie und Geodäsie，Frankfurt am Main，Germany.

Kang G F，Bai C H，Gao G M.2008.Periodical characteristics of the geomagnetic secular variation and length－of－day variation.ChineseJournalofGeophysics（in Chinese），51（2）：369－375.

Koot L，Rivoldini A，Viron O D，et al.2008.Estimation of Earth interior parameters from a Bayesian inversion of very long baseline interferometry nutation time series.J.Geophys.Res.，113：B08414.doi：10.1029／2007JB005409.

Lambert S B，Dehant V.2007.The Earth′s core parameters as seen by the VLBI.AstronomyandAstrophysics，469（2）：777－781.

Langel R A，Estes R H.1982.A geomagnetic field spectrum.Geophys.Res.Lett.，9（4）：250－253.

Mathews P M，Herring T A，Buffett B A.2002.Modeling of nutation and precession：New nutation series for nonrigid Earth and insights into the Earth′s interior.J.Geophys.Res.，107（B4）：ETG 3－1－ETG 3－26.

Mathews P M，Guo J Y.2005.Viscoelectromagnetic coupling in precession－nutation theory.J.Geophys.Res.，110，2402，doi：10.1029／2003JB002915.

Olsen N，Mandea M，Sabaka T J，et al.2009.CHAOS－2－a geomagnetic field model derived from one decade of continuous satellite data.Geophys.J.Int.，179：1477－1487.

Rosat S，Lambert S B.2009.Free core nutation resonance parameters from VLBI and superconducting gravimeter data.AstronomyandAstrophysics，503（1）：287－291.

Roosbeek F，Defraigne P，Feissel M，et al.1999.The free core nutation period stays between 431and 434sidereal days.Geophys.Res.Lett.，26（1）：131－134.

Souchay J，Loysel B，Kinoshita H，et al.1999.Corrections and new developments in rigid Earth nutation theory，III，Final tables REN－2000including crossed－nutation and spin－orbit coupling effects.AstronomyandAstrophysics，135：111－131.

Vauterin P.1998.Tsoft：Graphical and interactive software for the analysis of Earth tide data∥Ducarme B，Paquet P eds.Proceedings of the 13th International Symposium on Earth Tides.Brussels.Série Géophysique，481－486.

Vondrák J，Weber R，Ron C.2005.Free core nutation：direct observations and resonance effects.AstronomyandAstrophysics，444（1）：297－303.

Vondrak J，Ron C.2009.Stability of period and quality factor of free core nutation.ActaGeodyn.Geomater.，6（3）：217－224.

Xu J Q，Hsu H Z Sun H P，et al.1999.Investigation of the Earth′s nearly diurnal free wobble resonance using tidal gravity observations with superconducting gravimeters.ChineseJournal ofGeophysics（in Chinese），42（5）：599－608.

Xu J Q，Sun H P.2009.Temporal variations in free core nutation period.Earthq.Sci.，22（4）：331－336.

Zhang H W，Tan B P.1995.The test of main nutation amplitude and free core nutation.JournalofInstituteofSurveyingand Mapping（in Chinese），12（1）：13－18.

附中文参考文献

郭金运，韩延本.2008.由SLR观测的日长和极移季节性和年际变化（1993～2006年）.科学通报，53（21）：2562－2568.

康国发，白春华，高国明.2008.地磁场长期变化和日长十年尺度变化的周期特征.地球物理学报，51（2）：369－375.

徐建桥，许厚泽，孙和平等.1999.利用超导重力仪观测资料检测地球近周日共振.地球物理学报，42（5）：599－608.

张捍卫，覃伯平.1995.主要章动项振幅与自由核章动的检测.解放军测绘学院学报，12（1）：13－18.