不同提升高度对气泡泵性能影响的理论与实验研究
赵荣祥 刘道平 梁 俣 陈永军 陆引哲
(上海理工大学制冷技术研究所 上海 200093)
目前关于气泡泵的实验研究主要集中在加热功率、沉浸比、竖直提升管的内径对气泡泵提升效率的影响等方面,对于提升高度的研究甚少。气泡泵[1],对Einstein制冷循环的性能有着至关重要的作用,其本质上是一段加热管——在气泡泵底部进行加热,产生上升气泡,由于浮力和摩擦阻力两者达到平衡,从而能够把液体“泵”到高位储液器中。对于气泡泵性能的研究,Delano等[2-3]建立了气泡泵的数学模型,研究了热量输入、提升管直径、沉浸比对气泡泵性能的影响。Schcefer[4]在Delano模型的基础上,研究了直径、沉浸比、液体提升量和热量输入之间的关系。王汝金等[1]研究了气泡泵沉浸比、提升管内径、加热功率与气泡泵的提升效率之间的关系。汤成伟等[5-6]研究了不同实验工况条件下的气泡泵的性能,得出了气泡泵的液体提升量以及提升效率与提升管管径,沉浸比和加热功率有关。针对在相同的加热功率、提升管内径和沉浸比条件下,研究不同的提升高度对于液体提升量及提升效率的影响甚少。
1 实验装置与实验方案
搭建此实验系统的主要目的是测试在相同的沉浸比、内管径、加热功率条件下,不同的提升高度对于液体提升量和气泡泵提升效率的影响。实验装置如下图1所示。整个装置主要由气泡泵、竖直提升管、高位储液器、低位储液器和测量系统组成。测量系统主要由量杯、秒表和电子秤组成,可直接测得液体的质量流量。系统的加热功率由电控箱控制调节,调节范围0~1000 W。为使实验更加准确,系统全部做保温处理。

1气泡发生装置 2竖直提升管 3高位储液器 4测量系统 5低位储液器6排液口7电控箱8补水箱9补水阀10液位计
系统运行条件:压力为一个标准大气压(开式系统),温度为100 ℃的饱和状态,工质为水。
具体实验方案:竖直提升管采用玻璃管,内径都为7 mm,内径表面粗糙度相同,高度分别为600 mm和800 mm,在相同的沉浸比(H/L)下(H/L分别取0.2,0.3,0.4,0.5),加热功率依次取100 W、150 W、200 W、250 W、300 W、350 W、400 W、450 W、500 W、550 W、600 W、650 W,通过测量单位时间内液体的提升量,分析不同的提升高度(如下图2所示)对液体提升量的影响。从图中可以看出,以沉浸比都等于0.5为例,800 mm高度的提升管比600 mm的提升管多提升100 mm。

图2 不同提升高度的对比图
2 气泡泵流动模型的建立
本实验的流动模型采用均相流模型[7]。由于实验是在提升管内径相同、沉浸比相同的条件下,研究不同的提升高度对于液体提升量的影响,在平亚琴建立的流动模型[8]基础上建立新的气泡泵模型。为简化计算,本模型基于以下假设:1)由于采取了足够的保温措施,故认为整个系统绝热。2) 气泡泵在提升效率最大的弹状流下稳定工作。3) 系统流动压头与流动阻力相等。4)由于提升高度不同产生的提升后液体的重力势能不同忽略不计。
2.1 管内两相流流动压头
由气泡泵的工作原理可得[9],提升管内两相流的流动压头,是液体高度H产生的推动力:
Sflow=ρlgH-[αρg+(1-α)ρl]gL
(1)
式中:Sflow为流动压头,Pa;ρgρl为分别为储液器内气体和液体的密度,kg/m3;H为储液器的相对液位高度,m;L为气泡泵的提升高度,m;α为截面含气率,由下式计算得出:
(2)
式中:Qg、Ql分别为气相和液相的体积流量; m3/s;A为提升管的截面面积,m2;D为提升管内径,m。
2.2 两相流流动阻力
由图1可知,流动阻力可分为管内流动阻力、沿程阻力和局部阻力。
2.2.1管内两相流流动阻力
两相流在竖直管内流动的总阻力为三部分压降之和——摩擦压降、重力压降和加速压降[8]。
1)重位压降
重位压降与两相流的密度沿通道长度变化有关,即与加热方式有关,对于绝热通道,α沿通道长度不变,流体流过直管时的重位压力梯度[7]为:
(3)
式中:θ为直管的水平倾角,对于垂直的上升管,θ=90°; g为重力加速度,m/s2。
2)加速压降
均相模型的加速压降的计算基于两相流的动量方程式,所研究的管段入口为饱和液体(x=0),在等截面通道内的加速压降梯度[7]为:
(4)
式中:xe为出口含气率;G为两相流的质量流速,kg/s。
3)摩擦压降
根据均相流流动模型,可以得到竖直提升管中两相流摩擦压降[7]:
(5)
(6)
(7)
式中:λl0为全液相摩擦阻力系数;φl0为全液相摩擦因子;υl为提升管内液相的比容, m3/kg;μl,μg分别为液相和气相的动力粘度,N·s/m2;X为Martinelli数[10]。
(8)
2.2.2沿程阻力和局部阻力
单相流从低位储液器流到气泡发生器产生的沿程阻力和局部阻力可按下式计算:

(9)
式中:λ为沿程损失系数,层流状态下的λ=64/Re;ρs为单相流体的密度,ρs=ρl;ke为进口损失系数,ke=0.5;kd为出口损失系数,kd=1;Ls、Ds分别为中间连接管的长度和直径;us为连接管内单相流体流速,m/s。
对于气泡发生器与竖直提升管相连接的渐缩口的压降△pTP,徐济鋆[11]提出了以下的计算方法:
对于均相流模型
(10)
其中,结合冯丽娜[12]提出的气体流量与加热功率的换算公式:
(11)
式中:γg为100 ℃饱和水蒸气气化潜热,2.26×106J/kg;ρg为100 ℃饱和水密度,0.59 kg/ m3。
综合以上公式可得气泡泵流动的计算模型:
Sflow=△Pa+△Pf+△P1+△PTP
(12)
联立公式(11)和(12)可以得到固定沉浸比、不同的提升高度下,液体的提升量与加热功率的关系。
3 量纲分析
量纲分析法[11],又称因次分析法(Actor Analysis Method),结合经验与实验数据,根据物理定律的量纲齐次原则,确定某种特定现象各物理量之间的关系,可以简化实验。
针对本实验的研究内容,主要考虑影响气泡泵提升性能的主要因素。这些影响因素主要包括沉浸比H/L、提升管内管径D、提升管的高度L,密度ρ,运动粘度μ,液体提升量Ql以及加热功率P。即:
Ql=f(H/L,ρ,μ,P,L,D)
(13)
气泡泵主要考虑的总变量为7个,它们的基本量纲由质量M、长度L及时间T组成,即n=7,r=3,故可以组成4个无量纲量。这里取D、ρ及P为基本物理量,则无量纲用幂指数形式表示为:
(14)

表1 各物理量的无量纲量
利用量纲和谐定理,得:
(15)
则气泡泵量纲分析关系式可以转化为π3=f(π1,π2,π4),代入上述等式得:
(16)
从上述的函数关系式中可以看出,在相同的沉浸比下,提升量与L/D(管长与管内径的比值)有关,根据实验结果,成反比关系,即在其他条件一致的条件下,比值越大,气泡泵的提升性能越差。
4 结果分析
4.1 理论结果与实验结果分析
以沉浸比都为0.5为例,得出液体提升量与加热功率关系的理论值与实验值,如下图3所示。

图3 理论值与实验值的对比
理论结果一直呈上升趋势,这是由于理论计算的基础是基于前面所提出的一系列假设。与理论计算的结果相似,实验结果表明:较大的提升高度对于提升量有负面影响。
4.2提升高度对液体提升量的影响
从图4和图5中可以看出,在相同的沉浸比、提升管内径,加热功率的实验条件下,提升管高度分别为600 mm和800 mm的气泡泵的液体提升量曲线大致相同。其他条件相同时,随着加热功率的增加,液体的提升量不断升高,当过了最佳加热功率时,液体的提升量开始下降,这是由于两相流的流型发生变化,不再是提升效率最大的弹状流。其他条件相同时,随着沉浸比的增加,液体的提升量不断上升。
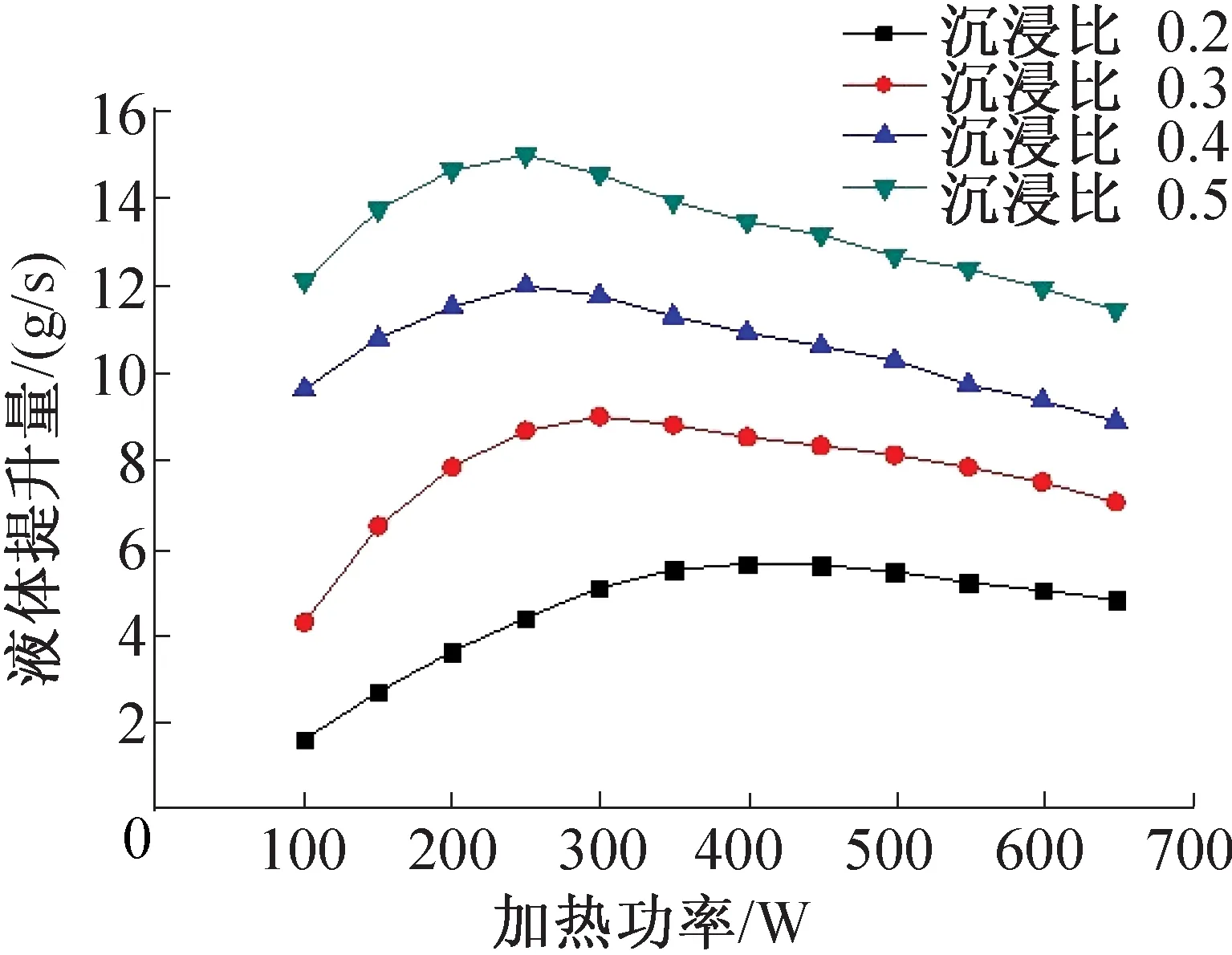
图4 L=600 mm时,气泡泵的液体提升量

图5 L=800 mm时,气泡泵的液体提升量
具体到某个沉浸比的情况,从图6中可以发现,以沉浸比为0.4为例,提升管L=800 mm的气泡泵的最大提升量为11.5 g/s,提升管L=600 mm的气泡泵为12 g/s,相差0.5 g/s。各加热功率相对应的液体提升量差值最大为0.78 g/s,减少8.12%的提升率。综合各沉浸比,出现差值最大的点为沉浸比为0.2、加热功率为100 W时,减少了10.5%的提升率,说明在低沉浸比低加热功率下,提升高度对于气泡泵的性能影响更大。
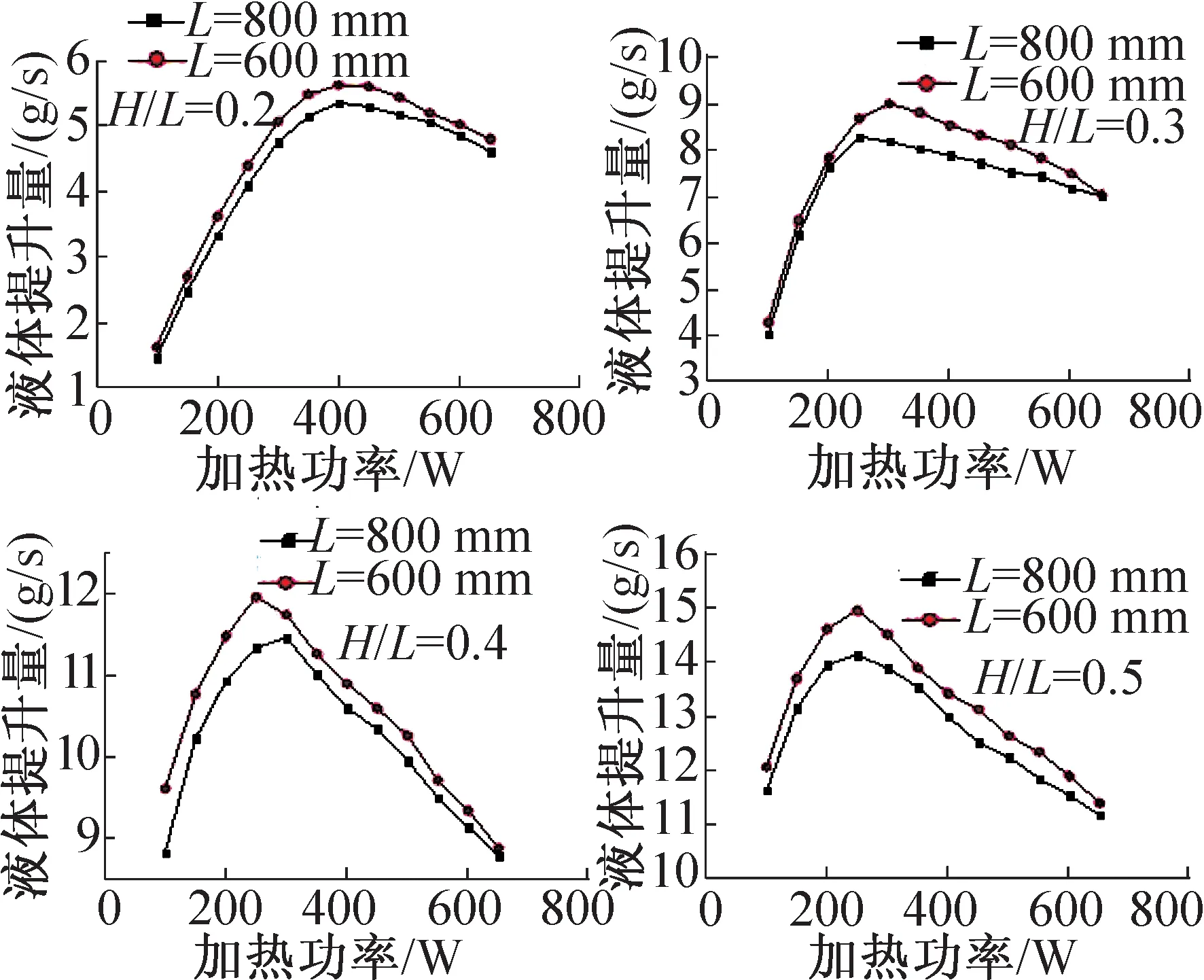
图6 不同沉浸比下,两种提升管液体提升量对比图
4.3 提升高度对气泡泵提升效率的影响
为了更好的分析评价不同的提升高度对于气泡泵性能的影响。根据传统水泵效率的相关概念,提出气泡泵提升效率的概念,即:
(16)
计算结果如图7和图8所示,在相同的沉浸比、提升管内径,加热功率下,提升管高度分别为600 mm和800 mm的气泡泵的效率曲线大致相同。在低沉浸比的条件下随着加热功率的增加,气泡泵的效率先升高达到一定的峰值后下降;在高沉浸比的条件下随着加热功率的增加,气泡泵的效率不断下降。其他条件相同时,随着沉浸比的增加,气泡泵的效率不断上升。从图中还可以发现,在相同的沉浸比、加热功率下,较大提升高度的提升效率反而较大,与提升量随着提升高度的增加而减少的结果正好相反。

图7 L=600 mm时,气泡泵的提升效率
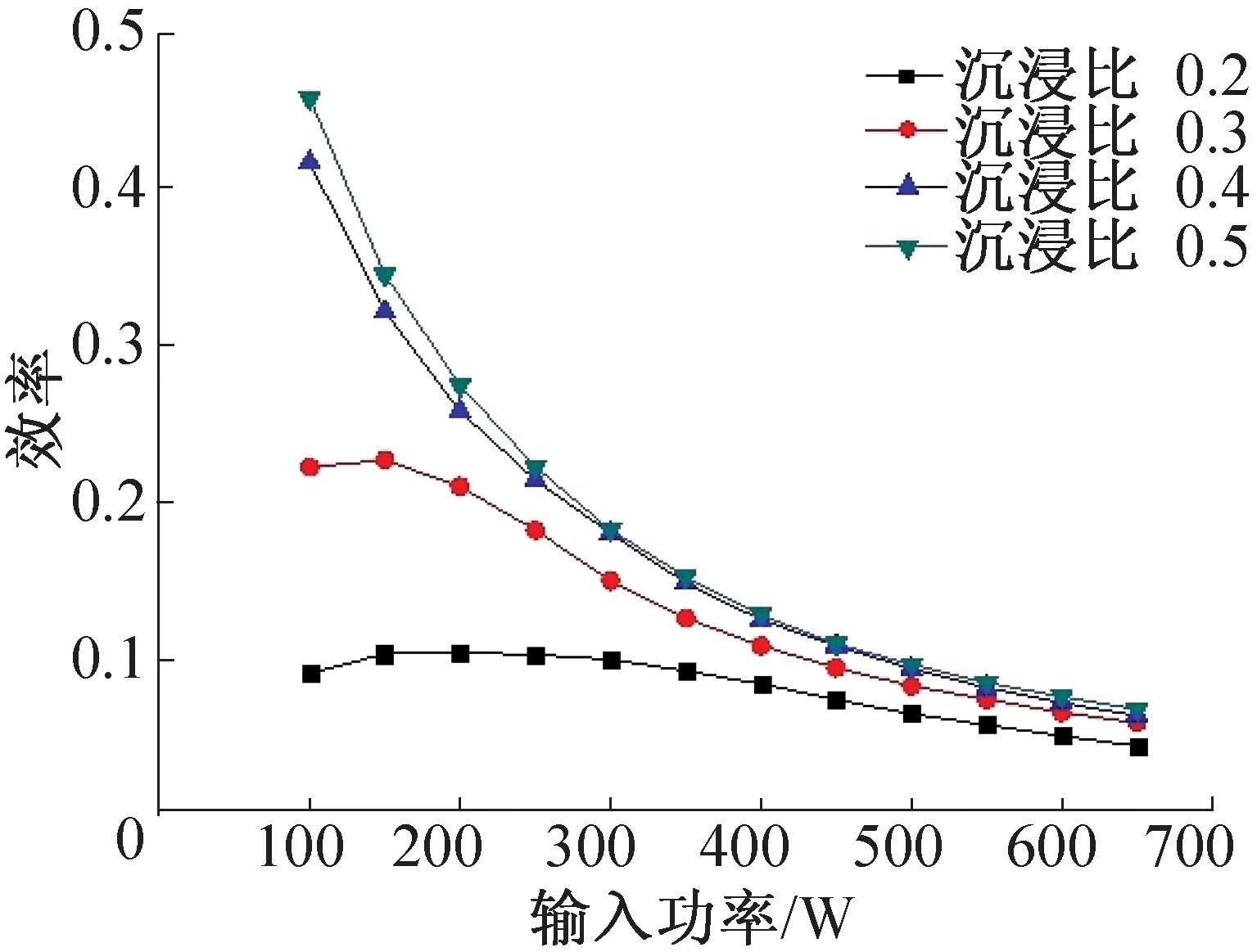
图8 L=800 mm时,气泡泵的提升效率
具体到某个沉浸比的情况,从图9中可以发现,提升管L=600 mm的气泡泵明显比提升管L=800 mm的气泡泵液体提升效率低,以沉浸比为0.4为例,提升管L=800 mm的气泡泵的最大提升效率为41.67%,提升管L=600 mm的气泡泵为34.01%,各加热功率相对应的液体提升效率差值最大为7.66%。综合各沉浸比,出现差值最大的点为沉浸比为0.5、加热功率为100 W时,减少了10.16%的提升效率。
通过上述实验结果的分析发现,随着沉浸比的不断提高,由不同提升高度所产生的提升量逐渐增大,提升效率也不断增大,进一步说明了沉浸比对于气泡泵性能的重要影响力。
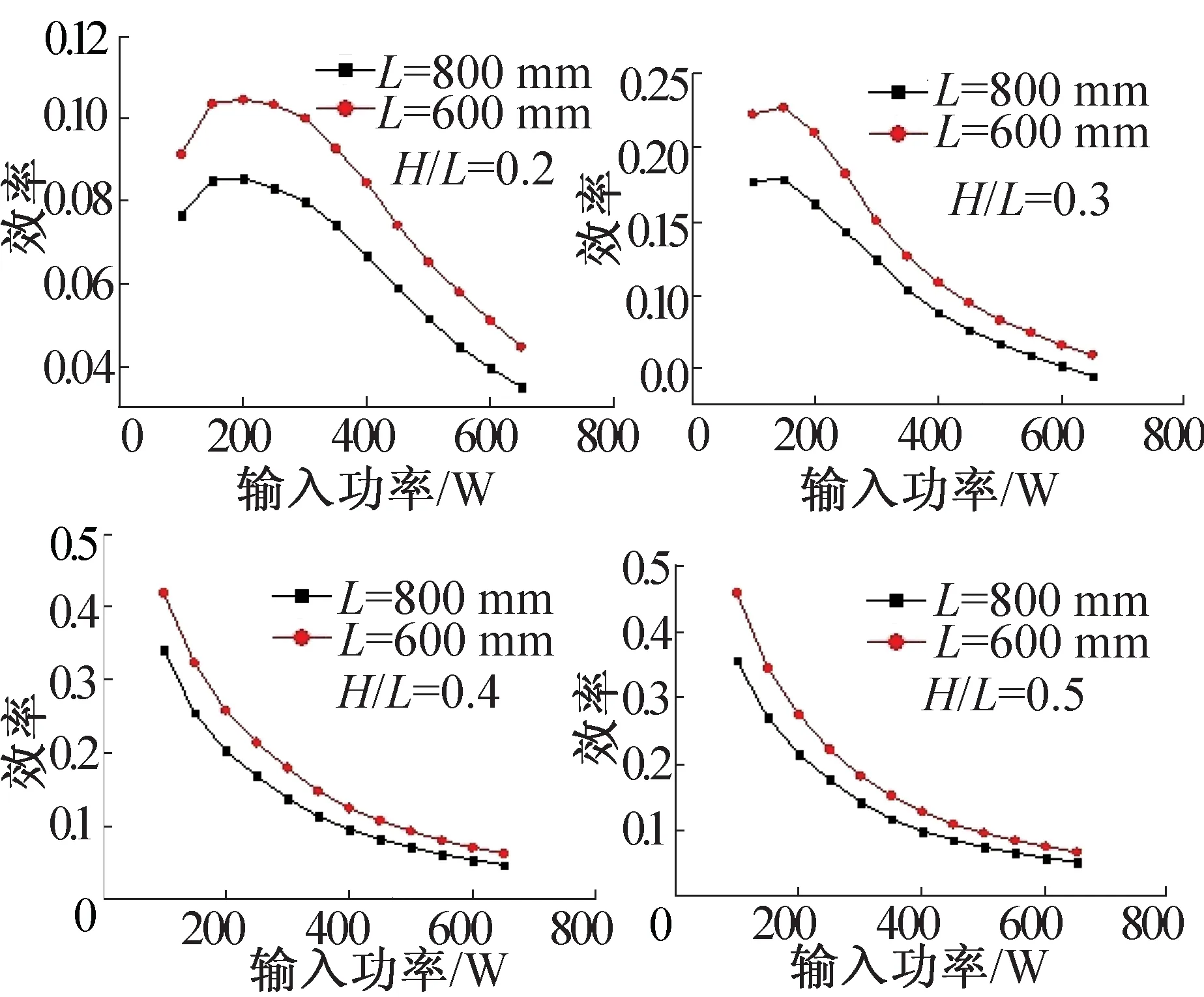
图9 不同沉浸比下,两种提升高度的效率对比
4.4 液体提升量对于Einstein制冷系统性能的影响
从Einstein制冷循环的原理[13]分析,液体提升量的减少,会导致冷凝吸收器中压力平衡剂的吸收不充分,降低了制冷剂的冷凝速度和压力平衡剂的吸收速度,降低了单位输入热量的利用效率,假设提升高度足够高导致气泡泵失效,此时的发生器继续加热,系统内压力上升,直至达到在吸收-冷凝器内氨和正丁烷气体同时被冷凝时的压力,极大地降低了整个制冷系统的COP,甚至影响系统的正常运行。由此可以看出,提升高度对于整个系统的性能有着重要影响。
5 结论
通过建立气泡泵管内两相流流动模型,对气泡泵性能参数进行无因次分析以及构建实验装置进行实验,可得出以下结论:
1)从实验结果和量纲分析可知,在沉浸比、加热功率、提升管内径等其他因素一致的条件下,气泡泵的液体提升量与L/D的比值成反比关系,即管长越长,液体提升量越少,提升效率与提升高度成正比关系。
2)通过管内流动模型的建立,确定了产生这种差别的原因。由于两相流流动的复杂性,本实验得出了一个定性的结果,即由于管长的增加,导致气泡泵流动压头,流动阻力的变化,最终导致液体提升量的减少。
3)由于管长的增加,两相流流态的改变可能也是导致这种差别的原因,有待进一步的研究。
4)对于不同提升高度的气泡泵实验和理论研究,为Einstein制冷循环系统中吸收-换热器液体喷淋位置、换热管布置等装置的设计提供了依据。
本文受上海市教育委员会科研创新项目(13ZZ117)和上海市研究生创新基金项目(JWCXSL1302)资助。(The project was supported by Innovation Program of Shanghai Municipal Education Commission(No.13ZZ117)and The Innovation Fund Project For Graduate Student of Shanghai(No.JWCXSL1302).)
[1] 王汝金, 刘道平, 薛相美, 等. 单压吸收式Einstein循环制冷机中气泡泵参数的设计确定[J]. 流体机械, 2008, 36(1):62-65. (Wang Rujin, Liu Daoping, Xue Xiangmei, et al.Parameter Design and Determination for Bubble Pump in Single-pressure Einstein Absorption Refrigerator [J]. Fluid Machinery, 2008, 36(1):62-65.)
[2] Delano A.Design Analysis of the Einstein Refrigeration cycle[D]. Atlanta, Georgia:Georgia Institute of Technology, 1998.
[3] Shelton SV, Delano A, Schaefer LA. Design analysis of the Einstein refrigeration cycle[C]// Proceedings of the Renewable and Advanced Energy Systems for the 21st Century, Lahaina, Maui, Hawaii, 1999.
[4] Schaefer LA.Single pressure absorption heat pump analysis[D]. Atlanta, Georgia: Georgia Institute of Technology, 2000.
[5] 汤成伟,刘道平, 祁影霞, 等. 单压吸收式Einstein循环制冷机中气泡泵的性能分析[J].制冷学报, 2009, 30(3):35-39. (Tang Chengwei, Liu Daoping, Qi Yingxia, et al. Experimental investigation on bubble pump in Einstein refrigeration cycle[J]. Journal of Refrigeration, 2009, 30(3):35-39.)
[6] 汤成伟, 祁影霞, 刘道平, 等. Einstein制冷循环中气泡泵的试验研究[J]. 低温与超导, 2009, 37(11):55-59. (Tang Chengwei, Qi Yingxia, Liu Daoping, et al. Experimental investigation on bubble pump in Einstein refrigeration cycle [J]. Cryogenics and Superconductivity, 2009, 37(11):55-59.)
[7] 阎昌琪.气液两相流[M]. 哈尔滨: 哈尔滨工程大学出版社, 2007: 165-167.
[8] 平亚琴, 刘道平, 陈盛祥, 等. 单压吸收式制冷系统气泡泵理论模型与实验研究[J]. 制冷学报, 2010, 31(6):46-50. (Ping Yaqin, Liu Daoping, Chen Shengxiang,et al. Theoretical Model and Experimental Analysis of Bubble Pump in Single-pressure Absorption Refrigeration System[J]. Journal of Refrigeration, 2010, 31(6):46-50.)
[9] 阙雄才, 李红. 热虹吸泵绝热弹状流的热虹吸特性研究——无泵溴化锂吸收式太阳能制冷机机理研究之二[J]. 太阳能学报, 1986, 10(1):1-13.(Que Xiongcai, Li Hong. Study on thermal siphon characteristics of slugflow with heat insulation in thermal siphon pump-the second mechanism studies on pumpless LiBr absorptionsolar refrigeration machine[J]. Solar Energy Journal,1986,10(1): 1-13.)
[10] Hemik K T. Boiling vertical two-phase flow at sub-atmospheric pressure [J]. Heat and Mass Transfer, 1998(41):2909-2924.
[11] 徐济鋆. 沸腾传热和气液两相流[M] 原子能出版社,2010:133.
[12] 冯丽娜,刘道平,陈翠云,等. 气泡泵冷态实验研究及性能参数的无因次分析[J]. 制冷学报,2013,34(2):44-48.(Feng Lina, Liu Daoping, Chen Cuiyun, et al. Experimental Study on Bubble Pump Under the Cold State and Non-dimensional Analysis of System Performance Parameters[J].Journal of Refrigeration,2013,34(2):44-48.)
[13] 宋玫峰,刘道平, 黄文件. 单压吸收式制冷技术的发展[J]. 暖通空调,2005(3):31-35.(Song Meifeng, Liu Daoping, Huang Wenjian. Development of Single Pressure Absorption-type Refrigeration Technology[J]. Journal of HV&AC,2005(3):31-35.)

