均匀照明方形光斑的LED自由曲面透镜设计
张 康,苏成悦,王维江
(广东工业大学 物理与光电工程学院,广东 广州 510006)
1 引言
LED由于其寿命长、能耗低等优点,在各个领域得到了广泛的应用,如道路照明、投影机以及室内照明等[1]。但是由于LED光源发出的光近似朗伯型,发散角度比较大,这就需要对LED光源进行二次配光设计,来满足目标照明面的要求[2~3]。
目前自由曲面的求解方法主要有:剪裁法、划分网格法和SMS法。Ries等人提出了剪裁法,其基本思想是根据目标面的照度分布和光源特性建立一个关于光学面形的非线性偏微分方程组,通过解这个微分方程组得到光学面形[4~6]。丁毅等提出了基于偏微分方程组数值求解法得到了用于均匀照明的自由曲面透镜和反射器[7~8]。蒋金波等提出基于光学扩展量守恒的LED路灯透镜设计[9]。划分网格法的基本思路是根据边缘光线理论,通过求解能量守恒方程,得到光源每个小网格与目标平面每个小网格能量的对应关系,最后,通过斯涅耳定律构造自由曲面。王洪等人利用划分网格法得到了矩形光斑的自由曲面透镜和反射器[10]。王恺等人提出非圆对称自由曲面透镜的算法[11]。上述方法都是针对点光源,当光源尺寸较大时,目标面的光斑会出现较大的恶化。SMS法针对扩展光源设计,可同时设计透镜的多个表面,从而控制光源发出的两个波面,变换成给定的两个输出波面,但是这种方法求解比较繁琐,设计难度大。
本文以非成像光学原理为基础,利用划分网格的方法,在特定的坐标系内建立光源面与目标面网格的对应关系,设计了一种适用于大功率LED均匀照明的自由曲面透镜,该透镜实现了方形区域的均匀照明,并且当LED光源尺寸较大时,仍然能保持较高的能量利用率和照度均匀性,特别适用于投影显示和道路照明等领域。随着光源模组的应用推广,通过对形成方形光斑光源模组的拼接,可投射出各种矩形光斑,能应用于各种照明领域,因此对方形光斑的研究有较强的理论和应用价值。
2 设计原理
根据边缘光线理论,采用划分网格的方法设计自由曲面透镜。设计思路如下:首先建立LED光源与方形目标平面的能量对应关系;然后计算自由曲面透镜上的点坐标和法相矢量,得到自由曲面面形。
2.1 网格划分
根据光源与目标面的特点,对于光源选取空间球坐标系,网格划分如图1所示,对于目标面选取直角坐标系,网格划分如图2所示。光源位于坐标原点O,主光轴为z轴,沿着z轴方向的中心光强为I0,θ为光线与z轴的夹角,φ为光线在xoy平面内的投影与x轴的夹角。则光源发出的整体光通量为:
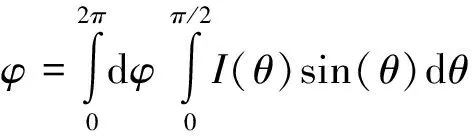
(1)
式中I(θ)=I0cos(θ)。
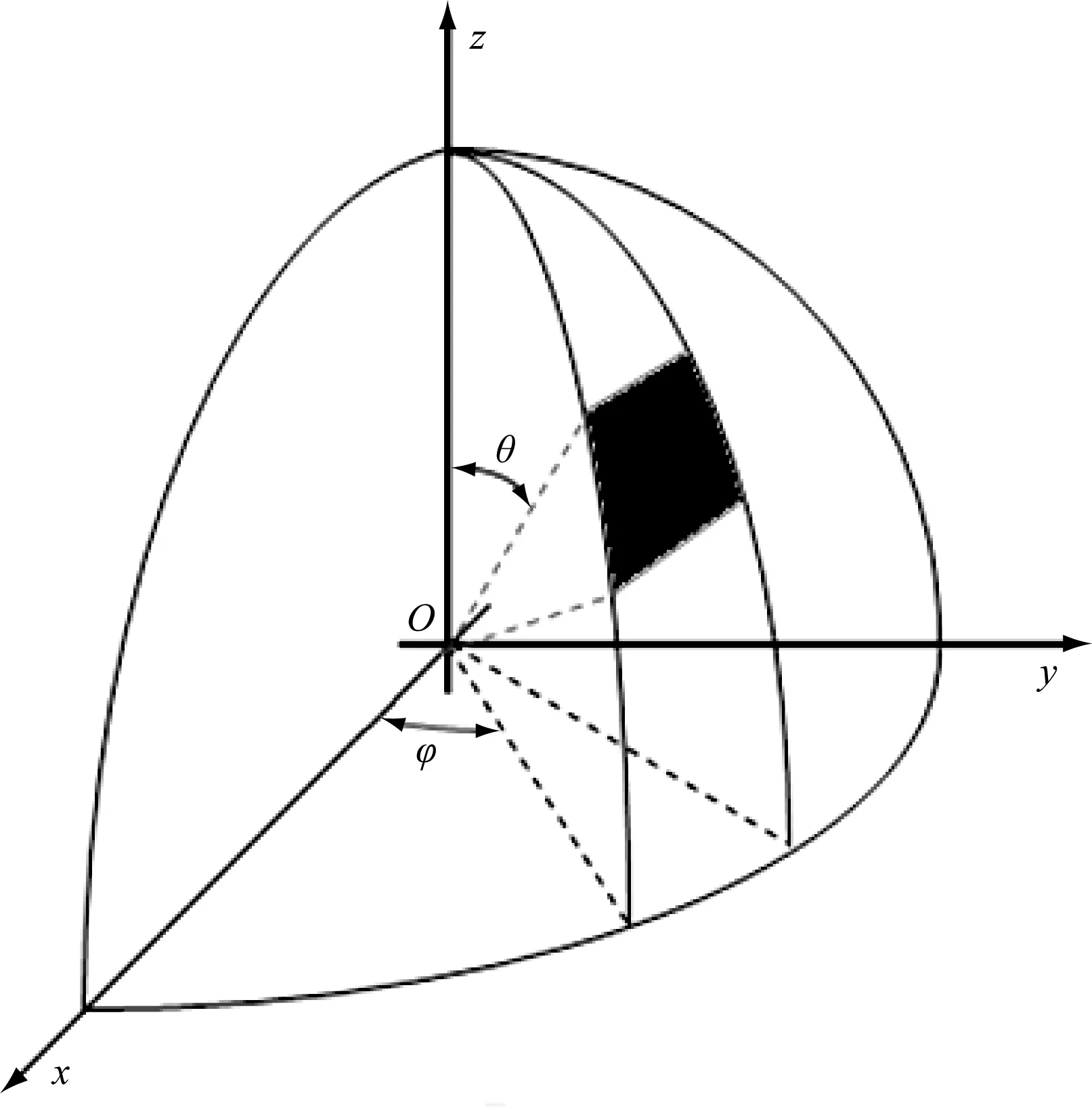
图1 光源网格划分Fig.1 Grid division of light source
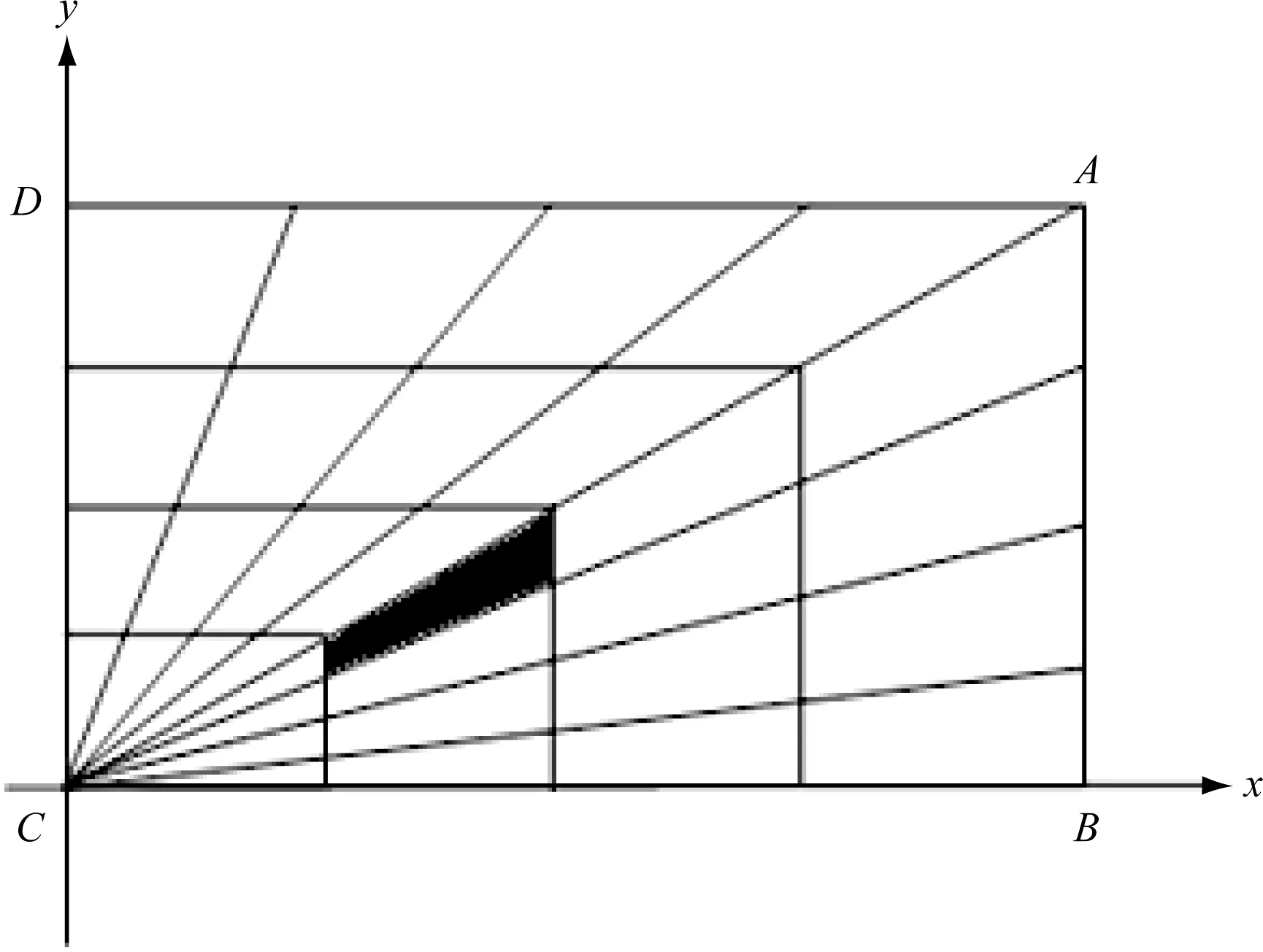
图2 目标平面网格划分Fig.2 Grid division of target plane
假设目标照明面的平均照度为Ev,该1/4方形区域的长和宽分别为a和b,中心线为AC,首先,将第一象限AB和AD等分为m份,将方形的中心线AC划分成n等分,这样就形成了2m×n个三角形。对应光源面,则是在φ角上分成2m份,θ角上分成n份。
根据能量守恒原理可得:
(2)
根据式(2),就可以求出一系列的θ值。同样,根据能量守恒有:
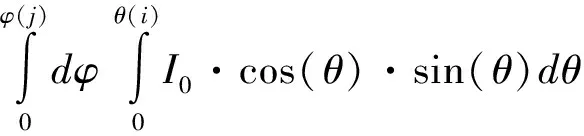
(3)
根据式(3)即可求得一系列的φ值。
2.2 构造自由曲面透镜
如图3所示,根据光源和目标照明面的能量对应关系在光源上选择一条初始光线I0,经自由曲面折射后对应于目标照明面上的初始位置Q0,我们选取P0(0,0,z0)作为光学表面面型顶点作为计算的初始点,光源位于坐标原点。由这两点坐标可求出初始光线入射光方向的单位矢量In和折射光方向的单位矢量Out,再由折射定律的矢量公式可求出自由曲面在初始点处的单位法矢量N为
(4)
式中n——自由曲面介质的折射率。
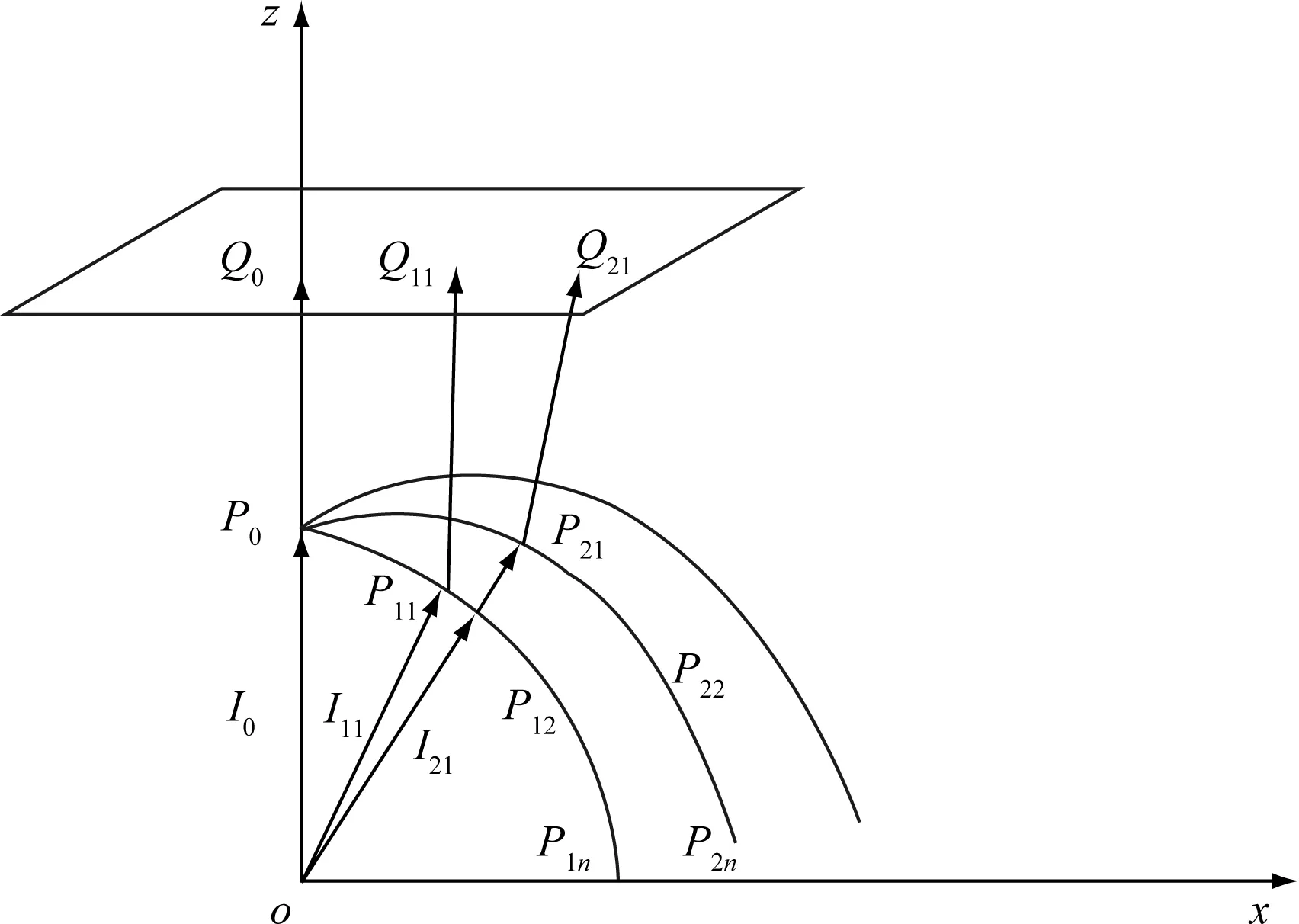
图3 自由曲面透镜表面生成示意图Fig.3 Sketch of generating freeform lens surface
由法矢量和初始点坐标可求出过P0点的切平面T0。根据光源和目标照明面的能量对应关系,在光源上选择第二条出射光线I11,经自由曲面折射后对应于目标照明面上的点Q11,光线I11与切平面T0的交点P11(x1,0,z1),由这两点坐标可求出光线I11入射光方向的单位矢量In11和折射光方向的单位矢量Out11,再由折射定律的矢量公式可求出自由曲面在P11点处的单位法矢量N11,按照上面的方法迭代,以此类推,依次求出P12到P1n,这样就可以得到第一条初始曲线。第二条曲线的顶点仍然是P0,与第一条曲线构造方法不同的是,第二条曲线上的第二点P21为相应的入射光线I21与前一条曲线上点P11的切平面的交点。按照求解一条曲线的方法,可以依次求出P21到P2n。在上述曲线构造过程中,P2i的真实法线方向与计算得出的法线方向存在一定的误差,保证误差角度小于5°,否则删除该条曲线,并重新计算初始曲线。按照上述方法,依次类推可以求得第三条直至第2M条曲线。
3 模拟与分析
为简化模型,所求透镜的内表面为半球面,LED位于坐标原点,LED发出的光线透过该内表面不发生偏折,透镜外表面即为自由曲面。假设透镜所用材料为PMMA,折射率为1.49,且光线通过时无损耗,即系统能量守恒。
实例设计:设计实现10m×10m正方形区域均匀照明。选取初始点坐标P0(0,0,10),即取透镜高度为10mm;光源距离目标面的距离H=3m。通过上述原理编程计算,求得离散的数据点,再将离散点导入到三维建模软件中,通过放样拟合成曲面,最后生成实体如图4所示,透镜纵向最大长度为11mm,横向最大长度为24mm。将该透镜导入到tracepro中,选取光源的尺寸为1mm×1mm进行光线追迹,光线数目为100万,模拟的光强分布图如图5所示,目标面照度图如图6所示。
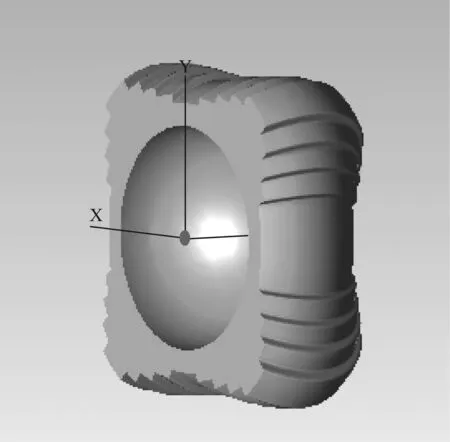
图4 透镜三维模型图Fig.4 3D model of the lens
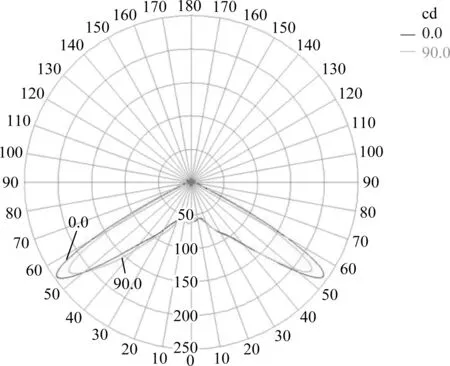
图5 极坐标光强分布图Fig.5 Polar Candela Distribution plot

图6 光源为1mm×1mm的照度图Fig.6 Illuminance map of 1mm×1mm source
为了更好的评价均匀照度透镜的性能,借鉴照度中的平台均匀度的概念,我们重新明确了照度平台均匀度的含义。即在照度曲线分布图中,平台段内的照度分布曲线的多个峰谷中,这些峰谷的最小照度和最大照度之比,即U=Emin/Emax,其值表征了平台区域内照度分布的均匀性,这里我们选择了其中一个方向进行讨论。从照度图中我们可以看出,目标面的照度均匀性为90%,系统光能利用率为88.2%,LED光强分布为蝙蝠翼配光。在距离光源不同的高度H处设置接收面,H变化时接收面上的能量利用率基本不受影响,均匀性略微有一点波动,可见系统的效率基本不受接收面高度H的影响。下面我们通过仿真的方法来讨论光源的尺寸变化对系统的影响,并确认了这款透镜适用于扩展光源配光。
3.1 光源尺寸对系统的影响
在其他条件不变的情况下,增大LED光源的尺寸,分析其配光效果以及LED尺寸对配光效果的影响。下面是光源尺寸为2mm×2mm,3mm×3mm,4mm×4mm,5mm×5mm的照度图,如图7~图10所示。根据上面的照度图,我们可以得到表1中的照度均匀度和能量利用率。
从表1数据我们可以看出:当光源尺寸增大时,接收面的能量利用率基本保持不变,而目标面的照度均匀性略有降低,但仍处于较高的水平。当光源尺寸与透镜高度尺寸之比为3∶10,1∶2.5,1∶2时,该比例已超过1∶5,可以理解为扩展光源的情况,目标面的照度均匀度都在80%以上,均匀性较高,这说明该透镜对一定尺寸比例的扩展光源仍然适用。
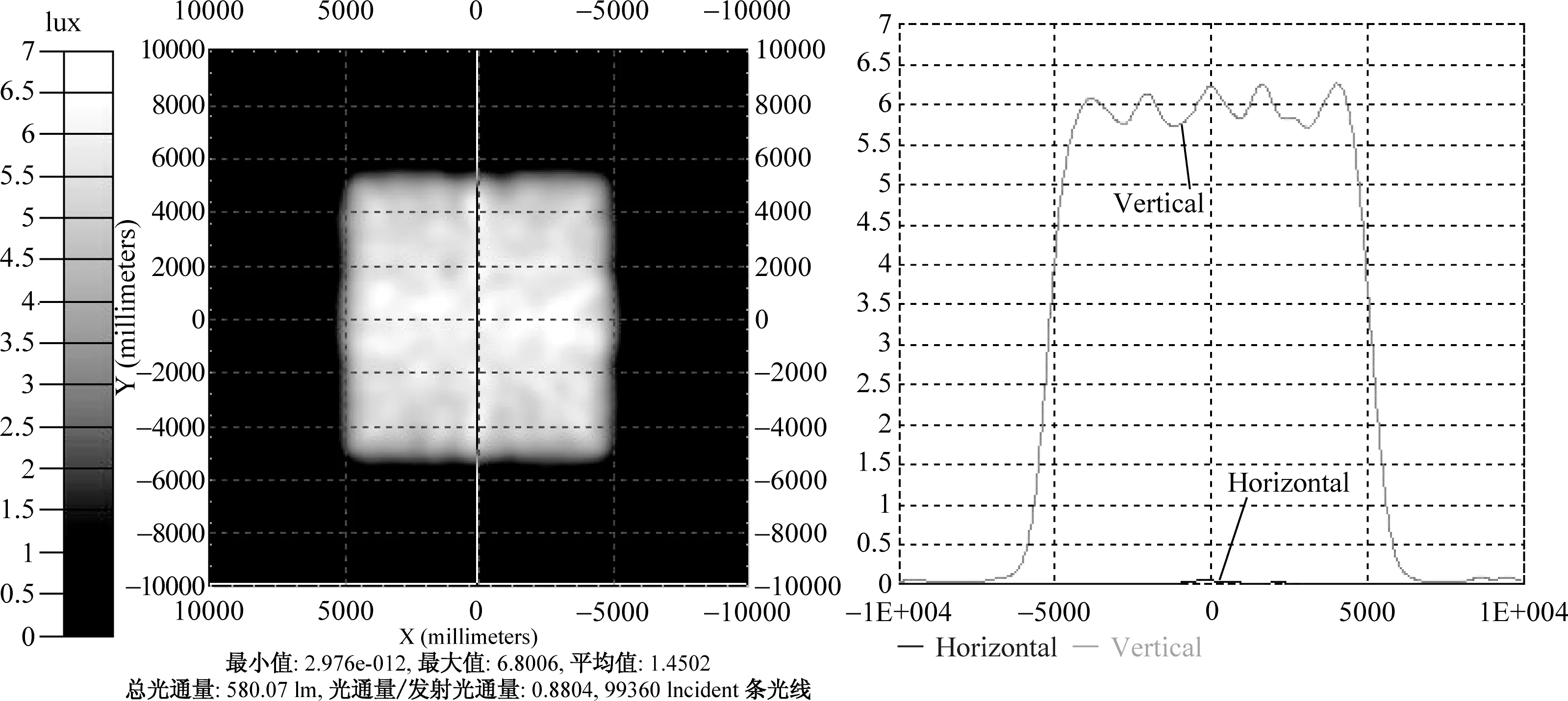
图7 光源为2mm×2mm的照度图Fig.7 Illuminance map of 2mm×2mm source
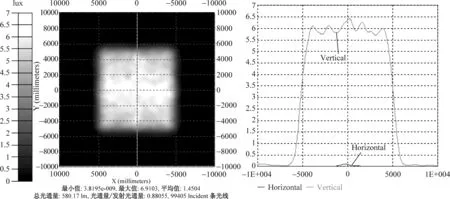
图8 光源为3mm×3mm的照度图Fig.8 Illuminance map of 3mm×3mm source
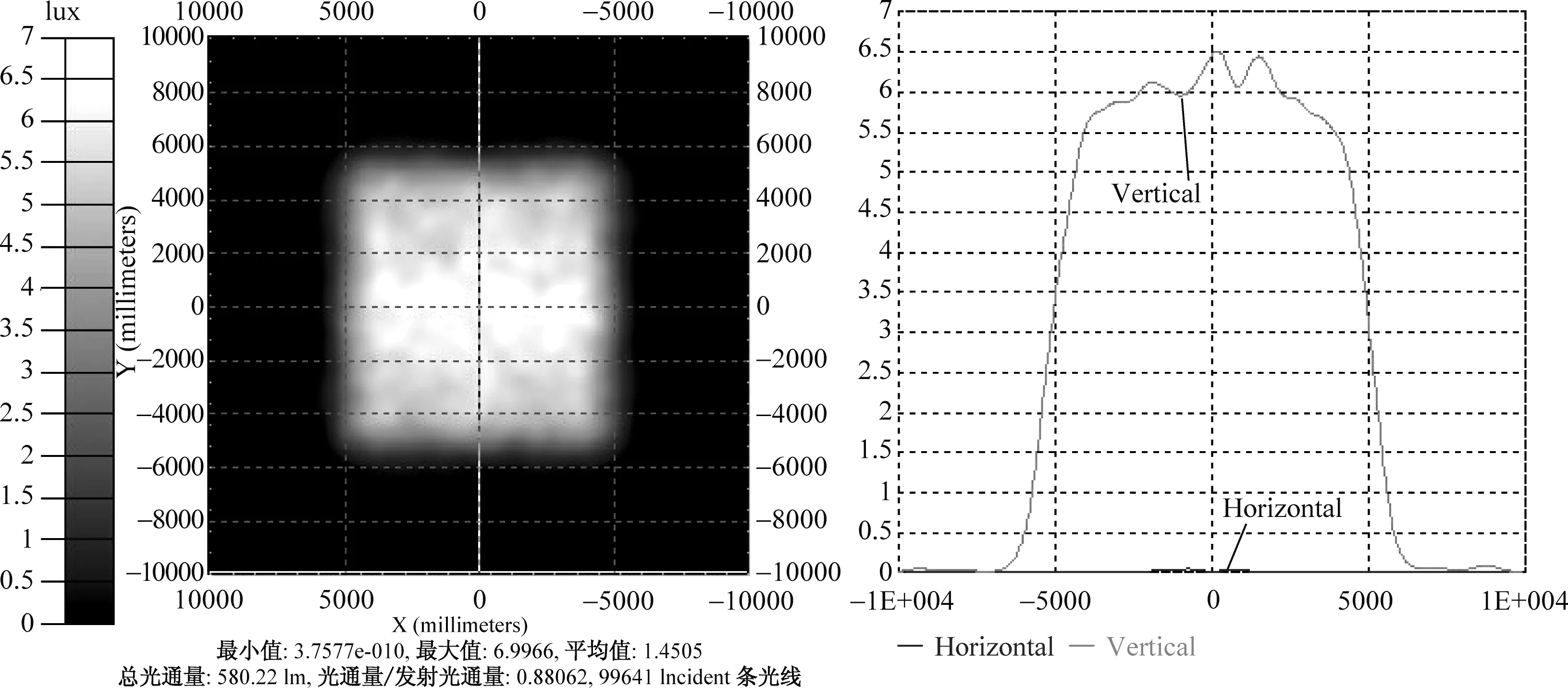
图9 光源为4mm×4mm的照度图Fig.9 Illuminance map of 4mm×4mm source
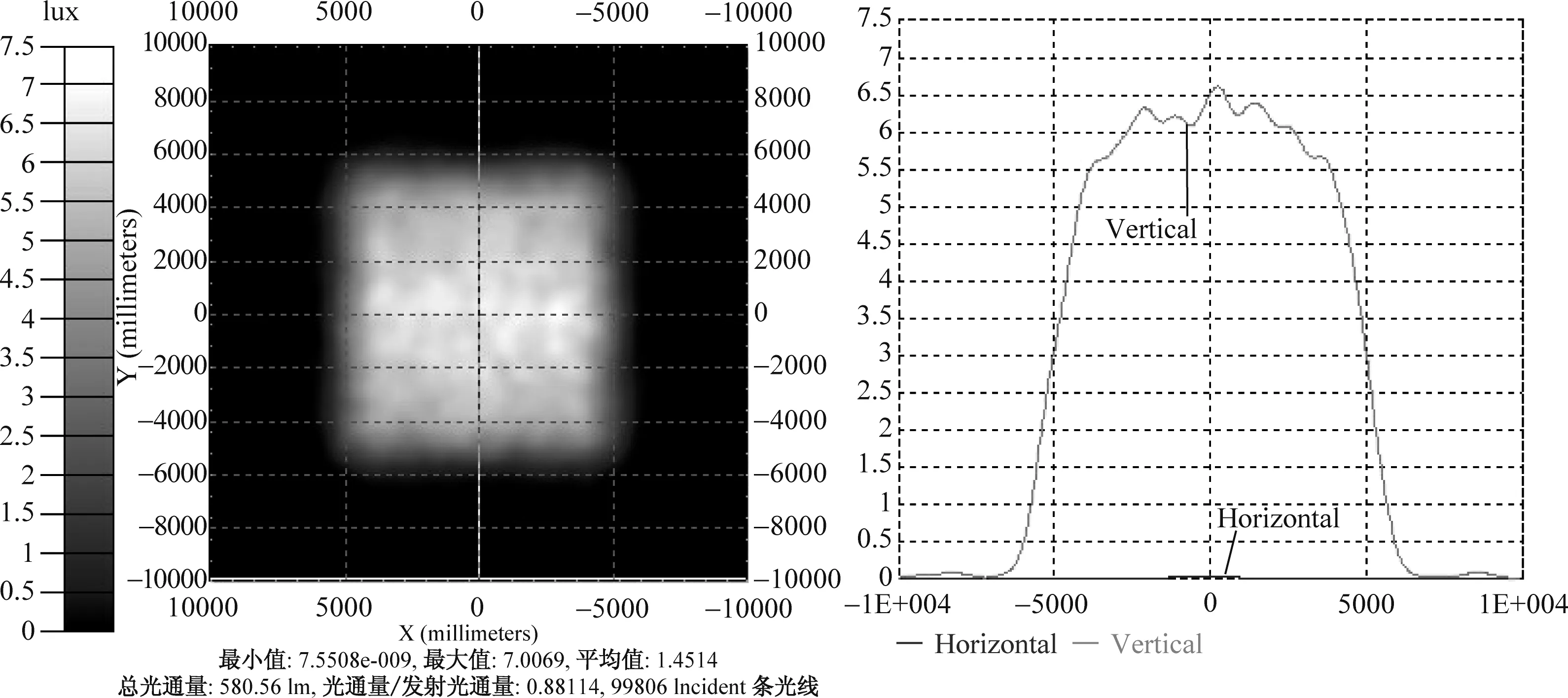
图10 光源为5mm×5mm的照度图Fig.10 Illuminance map of 5mm×5mm source
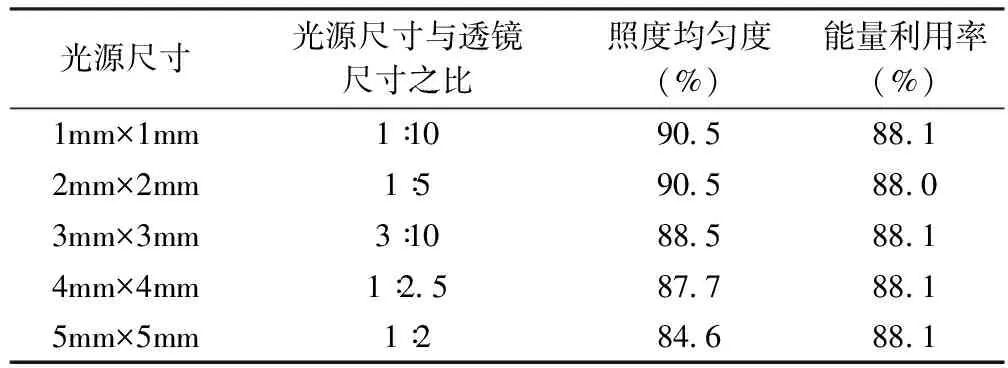
表1 光源尺寸对系统的影响Table 1 Influence of LED’s size on the system
3.2 光源尺寸为10mm×10mm的配光
针对更大尺寸的扩展光源,比如为10mm×10mm,如果仍使用上述透镜进行配光,此时光源尺寸与透镜尺寸之比为1∶1,仿真结果如图11所示,目标面的照度均匀光斑区域减小,只在约6mm×6mm的区域内保持较好的照度均匀性,边缘过渡区域变大。对于这种情况,可以通过对透镜高度的调整和优化来保证10mm×10mm区域内的照度均匀性,以达到设计要求。选取初始点坐标P0(0,0,20),即取透镜高度为20mm,重新按上述过程编程计算,建模仿真后,其照度图如图12所示,此时目标面均匀照度区域变大,照度均匀度为86%,照明效果得到了明显的改善。由此可见对于集成LED光源可以通过增大透镜的尺寸来完成配光,实现均匀照明的效果。
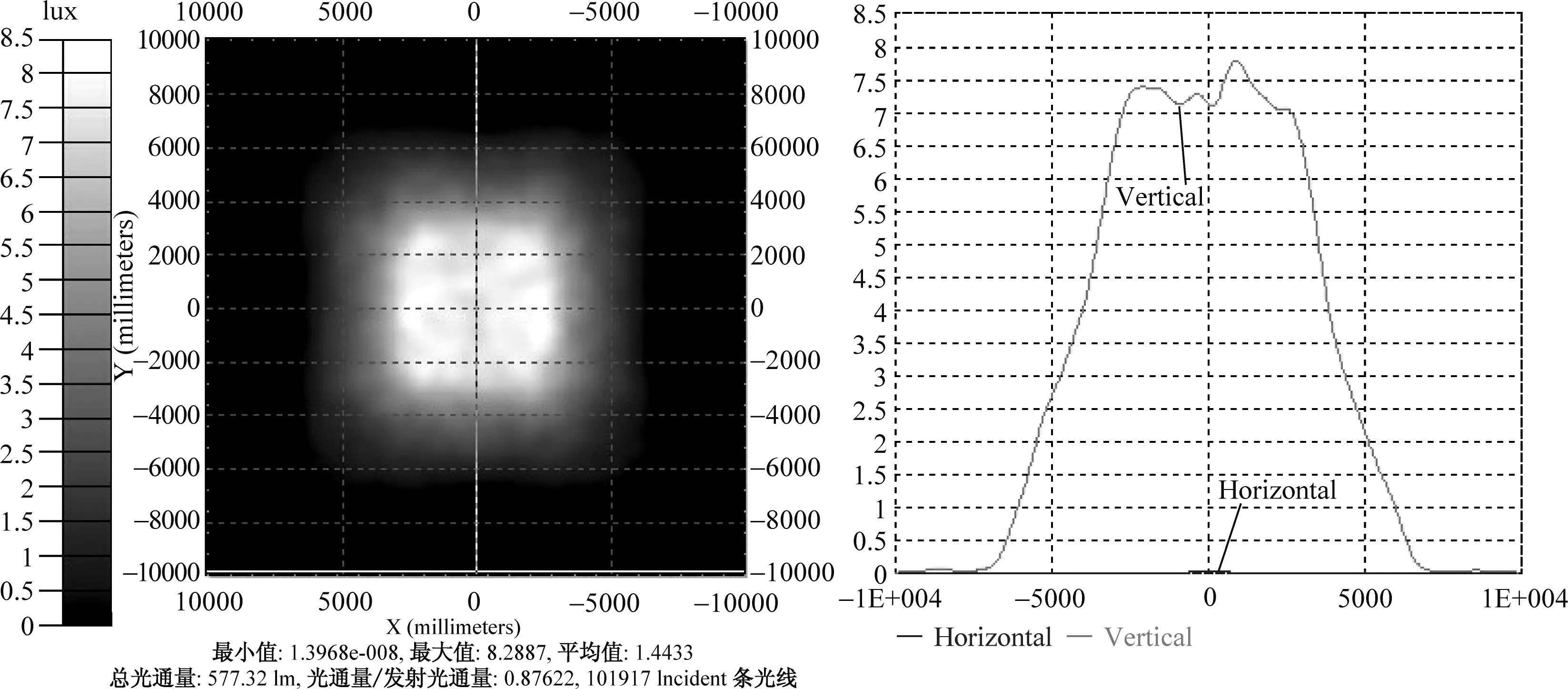
图11 透镜高度为10mm,光源为10mm×10mm的照度图Fig.11 Lens height is 10mm,illuminance map of 10mm×10mm source
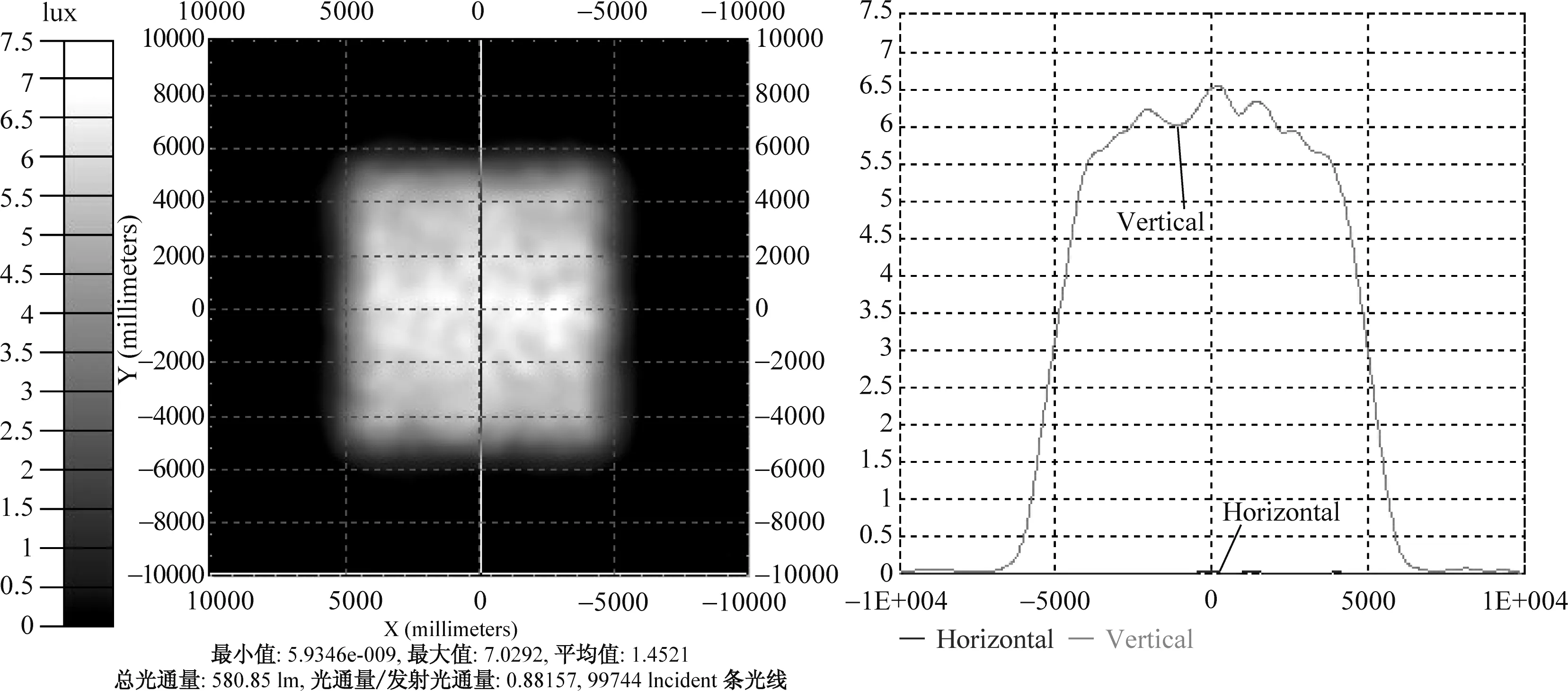
图12 透镜高度为20mm,光源为10mm×10mm的照度图Fig.12 Lens height is 20mm,illuminance map of 10mm×10mm source
4 结论
集成光源配光是目前研究的一个热点,因为计算困难也是配光设计的一个难点。本文根据边缘光线理论,选用划分网格法求解自由曲面,设计出针对集成光源的可实现方形区域内均匀照明的自由曲面LED透镜。光学仿真的结果表明:在透镜大小不变的情况下,增大LED的尺寸,当LED光源尺寸与透镜高度之比为1∶10和1∶5时,LED可被认为是点光源,目标面的照度均匀度高达90%,透镜的能量利用率为88%,这说明设计的透镜对点光源有较好的光学配光性能。当LED光源尺寸与透镜高度之比为3∶10等大于1∶5比例时,LED可被认为是扩展光源,目标面的照度均匀性有所降低,但均匀度在80%以上,仍然处于较高的水平,透镜的能量利用率在88%左右,基本保持不变,这说明该透镜对一定尺寸的扩展光源仍然适用。特别是当LED光源尺寸与透镜高度之比为1∶1时,照明区域均匀光斑区域变小,但通过优化透镜高度仍能达到设定的均匀照明区,获得理想的均匀照度。由于本方法设计的透镜可应用于LED集成光源,有较好的配光性能,适用于投影照明和室内外照明等领域,应用前景广阔。
[1] 史永胜,买迪,宁磊. 实现道路均匀照明的LED自由曲面透镜设计方法综述[J].照明工程学报,2010,21(5):73~77.
[2] 刘正权,孙耀杰,林燕丹.基于LED的自由曲面反射器设计软件研究[J].照明工程学报,2012,23(4):56~60.
[3] 周镇,苏成悦,付倩,等.一种基于自由曲面的LED准直透镜设计[J].应用光学, 2012,33(6):1058~1062.
[4] Ries H,Muschaweck J. Tailoring freeform lenses for illuminations[J]. SPIE, 2001,4442: 43~ 50.
[5] Ries H,Muschaweck J. Tailored freeform optical surfaces[J]. J. Opt. Soc. Am. A, 2002, 19(3): 590~ 595.
[6] Timinger A,Muschaweck J,Ries H. Designing tailored freeform surfaces for general illumination[J]. SPIE,2003,5186: 28~ 32.
[7] Ding Y,Liu X,Zheng ZR,et al. Freeform LED lens for uniform illumination[J]. Opt. Express, 2008,16(17):12958~ 12966.
[8] 丁毅,顾培夫. 实现均匀照明的自由曲面反射器[J].光学学报,2007,27(3): 540~544.
[9] 蒋金波,杜雪,李荣彬. LED路灯透镜的二次光学设计简介[J]. 照明工程学报,2008,19(4): 59~65.
[10] 王洪,张奇辉,张小凡,等. 实现道路均匀照明的自由曲面反射器设计[J].光电工程,2009,36(12):143~66.
[11] 王恺.大功率LED封装与应用的自由曲面光学研究[D]. 武汉:华中科技大学,2011.

