农村居民点空间分布特征及演变研究

陈伟强， 霍明明， 马月红， 高 颖， 张秩莹

(河南农业大学资源与环境学院，河南 郑州 450002)

中原经济区建设提出了以新型城镇化引领的“三化”协调发展战略，农村居民点已成为社会各界关注的热点，农村居民点正呈加速变化的趋势，农村居民点用地的变动映射了农村社会的发展变化历程[1].利用空间信息技术研究农村居点的空间布局和演变特征，对于掌握农村居民点变化规律，指导新农村布局规划，推动新型城镇化发展都有重要意义.空间统计分析是现代计量地理学中一个快速发展的方向和领域，其核心就是认识与地理位置相关的数据间的空间依赖、空间关联或空间自相关，通过空间位置建立数据间的统计关系[2].空间统计分析能很好解决土地利用空间格局变化等方面的问题，孙雁等[3]利用空间统计分析和景观格局指数分析法，研究了沈阳城区1910年以来土地利用空间格局变化.土地利用类型重心迁移是一种重要的空间统计分析方法，刘保晓等[4]利用土地类型空间格局重心指数研究了天津港区土地利用时空格局变化.农村居民点用地重心迁移可以从空间上描述农村居民点时空演变过程,描述土地利用的空间变化趋势[5].分形理论“Fractal”于20世纪70年代由美国学者曼德尔布罗特(Mandelbrot)创立，是当今世界十分风靡和活跃的新理论、新学科，横跨自然科学、社会科学及思维科学，目前已广泛用于土地利用形态研究[6～8].农村居民点具有不规则性、相对不稳定性和复杂性，同时也具有自相似性，可采用分形工具进行研究，明确农村居民点变化内在复杂性和稳定程度，得到传统的面积周长统计方法所不能表现的隐含信息，透过空间结构揭示其变化过程，弥补以往面积周长统计、景观指数等方法表达土地利用结构的不足[6,9].巩义市是全国百强县，经济发达，同时巩义市的地貌类型多样，农村居民点类型多种多样，以巩义市为例，开展农村居民点重心迁移和分形特征研究，对于揭示农村居民点发展规律，服务于村镇规划有重要意义.

1 研究区概况

巩义市位于河南省中西部，地处东经112°49＇～113°17＇，北纬34°13＇～34°52＇.巩义市工业基础较好，是全国乡镇企业发祥地之一，全国百强县.其地貌由山地、丘陵和河谷平原三大基本单元构成，地域差异十分明显，自东南向西北依次为山地、丘陵和河谷平原，山地、丘陵和河谷平原面积各占全市土地总面积的43.4%，45.3%和11.3%.

2 数据来源与研究方法

2.1数据来源

本研究数据来源于巩义市1990年第1次土地利用现状调查成果，以及2010年第2次土地利用现状调查变更成果.从1990年第1次土地利用现状调查成果中提取地类码为“52”的图斑，组成1990年农村居民点图层，从2010年第2次土地利用现状调查变更成果中，提取地类码为“203”的图斑，组成2010年农村居民点图层.在ARCGIS10.0系统中，通过数据投影与校正操作，将2期数据统一到西安80高斯投影坐标系.2期农村居民点空间分布数据如图1所示，空间图层的属性信息包括权属、地类、面积、周长、质心坐标等.

2.2研究方法

2.2.1 农村居民点空间重心测算方法 土地资源分布重心变化可以反映土地利用类型的时空演变过程[10，11].具体方法为：将空间上邻接的农村居民点图斑合并，然后计算合并后图斑的质心坐标，以图斑面积为权数，计算所有农村居民点图斑的加权质心坐标[5]，进而揭示农村居民点重心的空间转移规律.

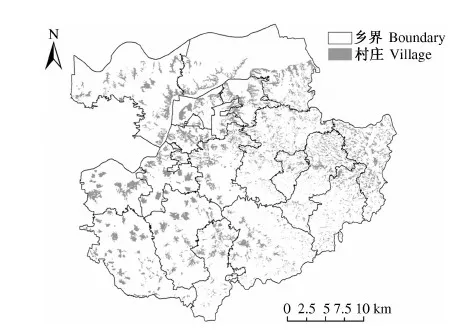
图1 1990年农村居民点分布图

(1)

式中:Xt，Yt分别表示第t年农村居民点重心坐标，xti，yti分别表示第t年农村居民点图层第i个图斑的质心坐标；ati表示第t年农村居民点图层第i个图斑的面积.

2.2.2 农村居民点分形维数测算方法 分形理论中的分形是指组成部分以某种方式与整体相似的几何形态，维数是几何对象的一个重要特征量[12].运用分形理论可以对各期农村居民点的形态结构进行定量化研究.

根据董连科[13]的推导，二维欧氏空间中，图斑周长与面积关系建立的分形结构模型为：

P1/D=k(1-D)/D·A1/2

(2)

经对数变换，可得：

(3)

式中：A为某图斑面积；P为同一图斑周长；D为分维数；k为待定常数；C为截距.

根据最小二乘线性回归原理，可以计算出待定系数D和C,D值越大，表示空间上的镶嵌结构越复杂，当D=1.5时，空间结构最不稳定.农村居民点地类空间结构稳定性指数SK的计算公式为：

SK=|1.5-D|

(4)

SK值越大，表示空间结构越稳定[5].

3 结果与分析

3.1农村居民点基本特征

将1990年和2010年2期农民居民点图层中的图斑进行相邻合并处理，统计孤立图斑的个数、图斑总面积、图斑平均面积、图斑总周长、图斑平均周长等指标，结果见表1.2010年比1990年图斑个数增加629个，图斑总面积增加1 209.41 hm2，平均面积增加311.04 m2，图斑总周长增加363 598.81 m, 平均周长增加0.66 m，可见经过20 a的发展，巩义市农村居民点的数量、总规模和个体平均规模均有不同程度增长.

表1 农村居民点基本特征

3.2农村居民点重心空间变化

利用ARCGIS10.0系统，分析1990年和2010年农村居民点重心坐标，1990年农村居民点X、Y重心坐标分别为410 641.14 m和3 842 938.22 m，2010年农村居民点X、Y重心坐标分别为410 440.74 m和3 842 121.35 m，见图2.经20 a的发展，巩义市农村居民点的重心向西南方向发生了偏移，东西向偏移200.41 m，南北向偏移816.87 m，偏移距离841.09 m.

图2 2010年农村居民点分布图

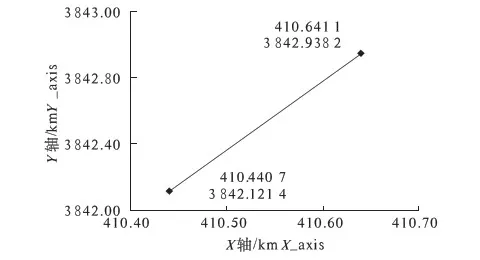
图3 1990～2010年农村居民点重心变化

以村图和2010年巩义市统计年鉴为基础，制作巩义市村级人口、GDP和人均纯收入分布图，利用空间重心测算方法，分别计算2010年巩义市人口重心，GDP重心和人均纯收入重心，并计算各自到1990年和2010年农村居民点重心的距离(表2).由表2可知，2010年农村居民点重心与人口重心、GDP重心和人均纯收入中的距离均小于1990年所对应的距离，这表明，农村居民点迁移过程中受人口、GDP和收入水平等因素牵引，向这些因素的重心处偏移.

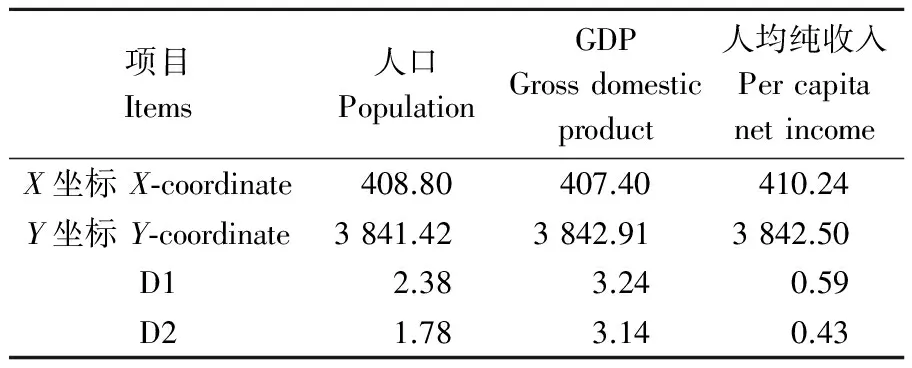
表2 人口、GDP和人均纯收入3因子重心与农村居民点的重心距离

将巩义市数字地型模型分别与1990年，2010年农村居民点图层叠加，计算各图斑的平均高程，并以图斑面积为权重，最终统计出1990年和2010年农村居点平均高程分别为256.5 m和265.9 m.结果显示出农村居民点并没有向海拔高度更低的平原区迁移，而是向矿产资源丰富的山地丘陵区迁移，这说明经济因素对农村居民点迁移的影响大于自然因素.

3.3农村居民点分形维数分析

根据计算公式(3)，将1990年和2010年农村居民点图斑的面积(A)和周长(P)做对数变换，利用SPSS系统进行回归分析，根据回归系数计算分维数D和稳定性指数SK，结果如表3所示.

1990年和2010年农村居民点分形结构模型的复相关系数分别为0.925和0.807，回归模型达到极显著水平.2期数据的分维数分别为1.113和1.077，在一定尺度下分维数的大小反映农村居民点的不规则程度和复杂程度，越不规则、越复杂，其分维数越大[5]，一般来说自然性强的地类，斑块形状比较复杂且无序，分维数的取值就高；人为干扰强的地类，图斑形状比较规则且简单，分维数的取值就小[14].巩义市农村居民点经过20 a的演变，分维数有所降低，说明农村居民点发展受人为干预作用大，形状趋于规则、简单.从稳定性指数看，经过20 a发展，巩义市的农村居民点更加趋于稳定.

表3 农村居民点分布形态的分形结构模型与分维数

分乡镇计算农村居民点的分维数与稳定性指数，结果见表4，从表4可以看出，各乡镇2期数据的分维数与稳定性指数各不相同，1990年分维数1.173～1.417，稳定性指数0.083～0.327，2010年分维数1.081～1.364，稳定性指数0.136～0.419.大峪沟镇、鲁庄镇、涉村镇、西村镇、新中镇5个乡镇的分维数呈增长趋势，稳定性指数呈下降趋势，其它10个乡镇和4个街道办事处反之.可见多数乡镇的分维数与稳定性指数与巩义市的整体变化趋势一致.

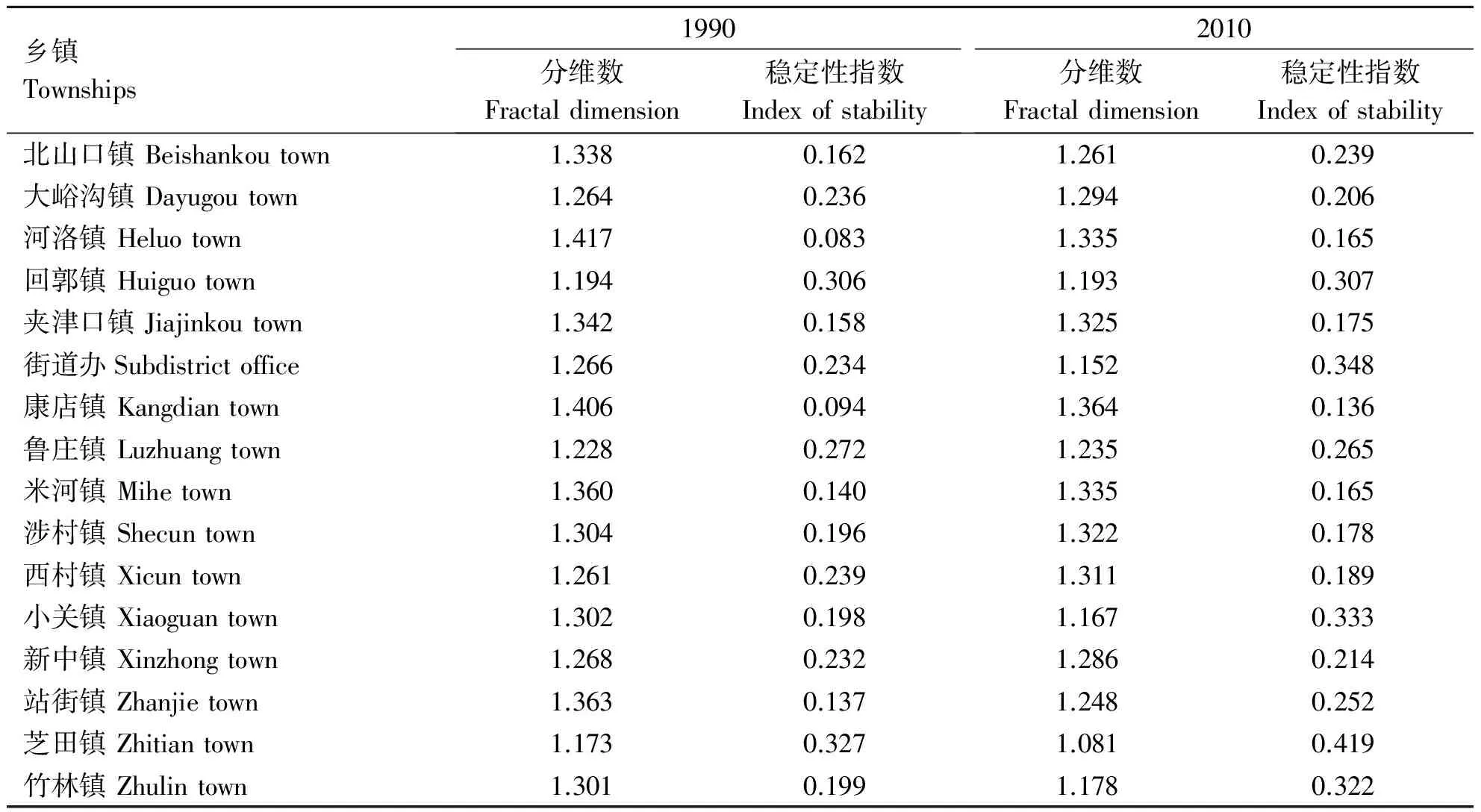
表4 各乡镇农村居民点分布形态的分维数与稳定性指数

将2010年和1990年巩义市各乡镇农村居民点分维数相减，求得2期数据的分维数差，利用ArcGIS的模式分析，可以分析分维数差的空间分布模式,高/低聚集度(High/Low Clustering)分析可以分析空间要素是否呈现聚类，G-统计量的Z得分可判断高值聚类和低值聚类[15]，局域G-统计量Z得分，可以表示空间上的高值聚类区或低值聚类区，也称“热点”(hot spots)分析[16].对农村居民点分维数差进行“热点”分析，结果见图4.图4表明，鲁庄镇和夹津口镇形成一个高值“热点”，说明“热点”区与相邻区是巩义市农村居民点分维数上升的区域，在北山口镇、大峪沟镇和街道办事处形成一个低值“热点”，说明该“热点”区与相邻区是巩义市农村居民点分维数下降的区域.

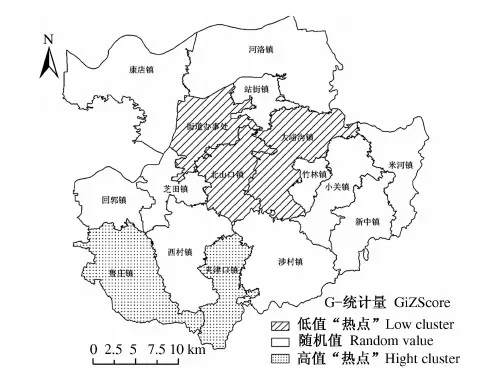
图4 分维数变化的“热点”分析

4 结论

本研究运用重心迁移和分形理论对巩义市1990年和2010年2时期农村居民点分布演变规律进行了研究.结果表明:1) 1990年到2010年农村居民点重心向西南方偏移，农村居民点迁移过程中受人口、GDP和收入水平等因素牵引，向这些因素的重心处偏移.2) 农村居民点并没有向海拔高度更低的平原区迁移，而是向矿产资源丰富的山地丘陵区迁移，这说明经济因素对农村居民点迁移的影响大于自然因素.3) 从1990年到2010年，巩义市农村居民点分维数有所降低，稳定性指数有所提高，说明农村居民点在人为作用下结构趋于简单，形态趋于稳定.4) 从1990年到2010年，巩义市有5个各乡镇的农村居民点分形维数演变趋势与巩义市整体演变趋势相反.5)农村居民点分维数差 “热点”分析结果表明，鲁庄镇和夹津口镇一带形成一个高值“热点”，北山口镇、大峪沟镇和街道办事处一带形成一个低值“热点”.

参考文献：

[1]李晓刚，欧名豪，许恒周.农村居民点用地动态变化及驱动力分析——以青岛市为例[J]. 国土资源科技管理, 2006,23(3):27-32.

[2]李 慧,王云鹏,李 岩,等.珠江三角洲典型地物空间分布特征研究[J]. 生态环境学报,2013，22(1)：164-169.

[3]孙 雁，刘志强，王秋兵,等. 191O年以来沈阳城区土地利用空间格局变化[J]. 中国土地科学，2012，26(9)：41-47.

[4]刘保晓,黄耀欢,付晶莹,等.天津港区土地利用时空格局变化与驱动力分析[J].地球信息科学学报,2012,14(2):270-278.

[5]郭碧云，王光谦，傅旭东,等. 黄河中游清涧河流域土地利用空间结构和分形模型[J]. 农业工程学报,2012,28(14):223-228.

[6]叶长盛，董玉祥. 珠江三角洲土地利用分形特征及其影响机制[J]. 农业工程学报, 2011,27(4):330-335.

[7]张竞竟，杨德刚，张豫芳,等. 基于GIS与分形理论的天山北坡城乡空间演变综合研究[J]. 资源科学,2007,29(6):83-89.

[8]李昭阳，汤 洁，孙平安，等．松嫩平原西南部土地利用动态变化的分形研究[J]．吉林大学学报：地球科学版，2006，36(2)：250-258．

[9]李新东，郭治兴，邓南荣，等．土地利用类型的分维值和稳定性指数空间变异分形[J]．生态环境，2007，16(2)：627-631．

[10] 魏 静，郑小刚，葛京凤.石家庄西部太行山区景观格局时空变化[J].生态学报,2007,27(5):1993-2001.

[11] 何艳芬,张 柏,马超群.松嫩平原土地盐碱化动态研究——以农安县为例[J].水土保持学报,2004,18(3):146-153.

[12] 徐建华．现代地理学中的数学方法[M]．北京：高等教育出版社，2002：392-401.

[13] 董连科.分形理论及其应用[M]．沈阳：辽宁科学技术出版社,1991：78-99.

[14] 沈中原,李占斌,武金慧,等．基于GIS的流域土地利用和土地覆被分形特征[J]．农业工程学报，2008，24(8)：63-67．

[15] GETIS A, ORD J K. The analysis of spatial association by use of distance statistics[J]. Geographical Analysis,1990,24:189-206.

[16] ORL J K, GETIS A. Local spatial autocorrelation statistics: distributional issues and an application[J]. Geographical Analysis,1995, 27:286-306.