淅川乌骨鸡生长和产蛋曲线的数学模型分析

田亚东，商鹏飞，焦显芹，康相涛

(1.河南农业大学牧医工程学院，河南 郑州 450002； 2.河南省家禽种质资源创新工程研究中心，河南 郑州 450002)

家禽的生长和产蛋受内在因素(品种、性别、体重、年龄)和外在环境因素(营养、温度、湿度、光照、通风)的影响，一般具有非线性的特性.可以根据实际生产中获得的数据，建立非线性数学模型来描述家禽生长和产蛋过程中某部分或整体的规律型变化.通过数学模型对家禽生长和产蛋曲线进行拟合和分析，可以动态地了解家禽的生长和产蛋过程，预测家禽的生长和产蛋规律，指导饲养管理和育种实践.在众多的非线性数学模型中，常用Gompertz,Logistic,Bertalanffy模型来拟合家禽的生长曲线[1～8].产蛋量是家禽非常重要的数量性状，家禽生产中产蛋曲线不但能够显示产蛋量的高低，反映饲养管理水平，而且能够为准确评估产蛋量性状的育种值提供依据.产蛋曲线模型的研究一直备受国内外遗传育种科研人员的关注.产蛋曲线数学模型的研究始于1971年，常用的数学模型有MILLAN提出的用以描述果蝇产卵过程的分室模型[9]和用以描述牛泌乳曲线的不完全函数及其修正形式的伍德模型[10]，杨宁等[11]在总结前人研究成果的基础上，提出了描述产蛋率曲线的改进数学模型.近年来，部分学者采用Gompertz,Logistic,Bertalanffy模型对家禽的累积产蛋数进行曲线拟合，也取得良好的效果[12,13].淅川乌骨鸡是产于河南淅川县的优良兼用型地方品种，也是目前所知的唯一白羽乌骨鸡产绿壳蛋的品种，2011年被列入《中国畜禽遗传资源志·家禽志》中[14].目前，针对淅川乌骨鸡生长和产蛋曲线数学模型的系统研究还没有报道.本研究拟用上述3种生长模型和3种产蛋曲线模型分别拟合淅川乌骨鸡的生长曲线和产蛋率曲线，为解析淅川乌骨鸡的生长和产蛋规律，合理利用淅川乌骨鸡种质资源及指导生产实践提供理论参考.

1 材料与方法

1.1试验材料

随机选取1日龄淅川乌骨鸡母雏600只，分育雏期、育雏期和产蛋期3阶段笼养至66周.0～8周为育雏期，9～18周为育成期，19周龄转入产蛋鸡舍笼养，每笼3只.育雏期采用颗粒料饲喂，育成期和产蛋期采用粉状料饲喂.

1.2试验饲粮

根据国家标准鸡饲养标准NY/T33-2004配制玉米-豆粕型试验饲粮，饲粮配方及主要营养成分见表1.

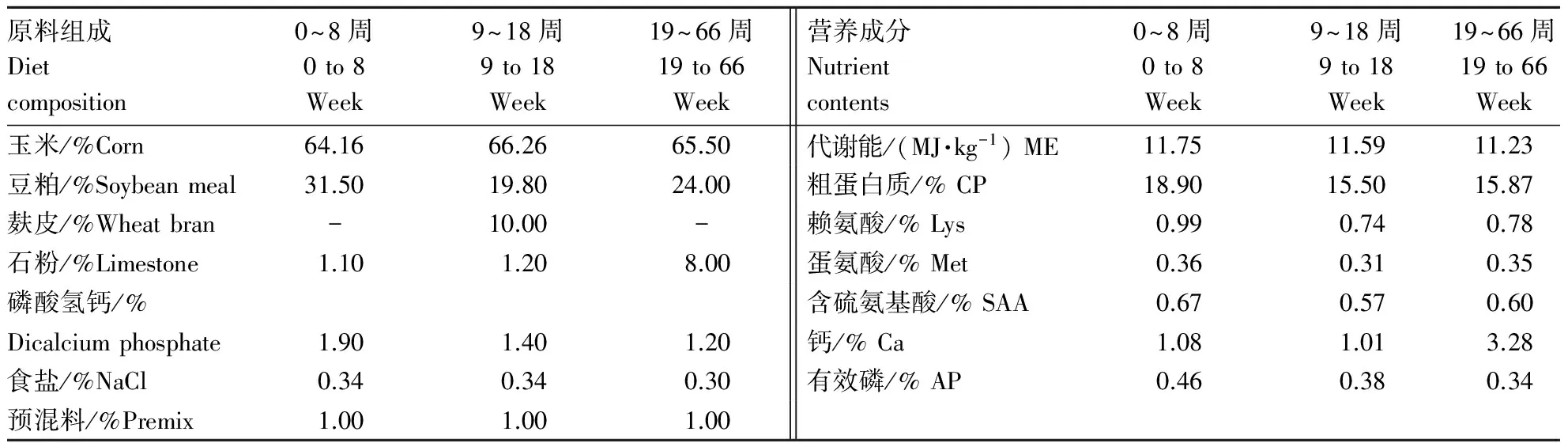
表1 饲粮组成及营养成分

1.3测定项目与数据处理

1.3.1 生长性能 从出壳至18周龄，每2周随机抽取50只，称取空腹体重，计算平均日增重.

1.3.2 产蛋性能 从21周至66周龄，每周记录产蛋总数和鸡只数，计算每周产蛋率.

1.3.3 生长曲线拟合 用Excel统计平均体重，绘制累积体重曲线，并采用SPSS11.5软件中Gompertz[1]，Logistic[2]和Bertalanffy[3]3种非线性生长模型进行拟合，公式如下：

Gompertz模型:Wt=A*exp(-B*exp(-Kt))，拐点(InB/K，A/e)；

Logistic模型:Wt=A/(1+B*exp(-Kt))，拐点(lnB/K，A/2)；

Bertalanffy模型:Wt=A*(1-B*exp(-Kt))3，拐点(ln(3B)/K，8A/27).

式中：Wt为t时的平均体重，A为成熟体重，K为生长速率，B为日龄调节参数.

1.3.4 产蛋率曲线拟合 用Excel统计周产蛋率，绘制各周产蛋率曲线，并采用SPSS 11.5软件中的伍德模型[9]、杨宁模型[10]、分室模型[11]对产蛋曲线进行拟合，公式如下：

伍德模型：yt=a*(t*b)*exp(-ct)；

杨宁模型：yt=a*exp(-bt)/[11][1+exp(-c*(t-d))]；

分室模型：Yt=a*(1-exp(-c*(t-d)))*exp(-bt).

式中：a，b，c和d为待定参数，t为产蛋周龄，yt为第t周的产蛋率.

2 结果与分析

2.1淅川乌骨鸡生长性能

淅川乌骨鸡0～18周龄的体重观测值见表2.由表2可知，淅川乌骨鸡在8～14周龄增重较快，平均日增重10 g以上，14周龄以后日增重逐渐下降.

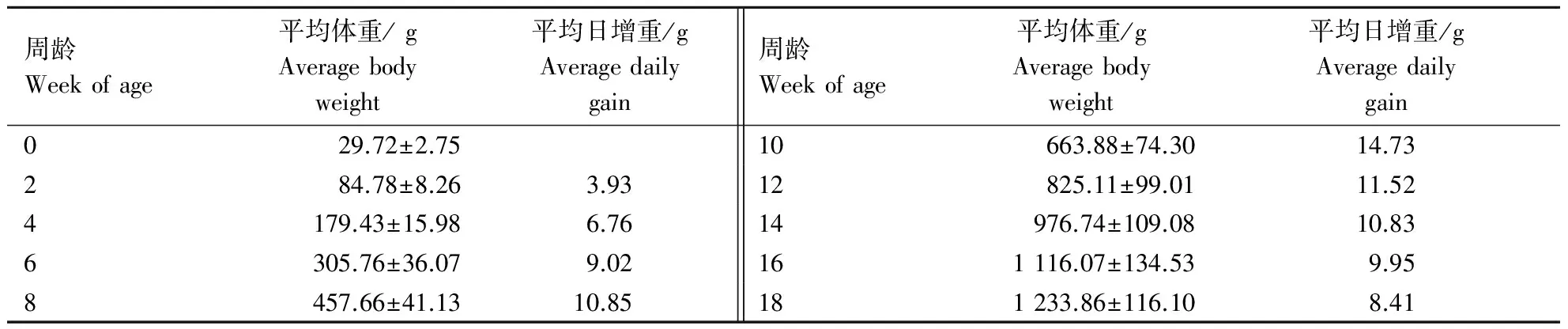
表2 淅川乌骨鸡0～18周龄体重观测值

2.2生长曲线拟合

根据淅川乌骨鸡生长性能测定数据，分别用Gompertz，Logistic和Bertalanffy 3种数学模型对淅川乌骨鸡生长曲线进行非线性回归拟合，拟合的模型参数以及3种生长模型曲线与体重实际观测曲线的比较分别见表3和图1.由表3可看出，3种生长曲线拟合后的数值与实际测定数值的相关指数R2(拟合度)均大于0.99，这表明3种生长模型均能较好地进行淅川乌骨鸡的生长曲线拟合，但Logistic模型拟合的成熟体重估计值比实际值低，生长拐点出现的较迟，拐点体重偏大；Bertalanffy模型拟合的成熟体重估计值比实际值高，生长拐点出现的较早，拐点体重小；而Gompertz模型参数估计值介于二者之间，最接近实际值.从拟合度上比较，也是Gompertz模型拟合度最高.由图1可看出，淅川乌骨鸡生长曲线呈S型，4周龄前生长缓慢，4周龄后逐步加快，在10周龄左右达到增重高峰期，之后生长速度开始下降.比较图1中的体重实际观测曲线和模型曲线，也可看出Logistic模型预测值4周龄前偏大，Bertalanffy模型预测值前期偏小；而Gompertz模型曲线与实际观测曲线基本吻合.根据成熟体重、生长拐点体重、生长拐点周龄、拟合度、与实际观测值的相近程度等5项指标综合分析，Gompertz模型是拟合淅川乌骨鸡生长曲线的最佳模型.

表3 3种非线性生长模型参数估计值及拟合度

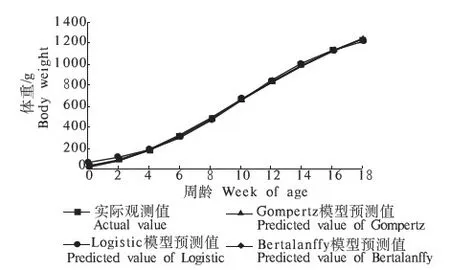
图1 淅川乌骨鸡生长模型曲线与实际观察曲线的比较

2.3淅川乌骨鸡产蛋性能

淅川乌骨鸡产蛋性能见表4.由表4可知，淅川乌骨鸡21周龄已有母鸡开产，开产后产蛋率上升较快，但整体上淅川乌骨鸡产蛋率偏低，高峰期产蛋率仅为65.5%，30周龄达产蛋高峰，65%以上产蛋率只维持3周左右，之后便开始缓慢下降，66周龄时产蛋率下降至33%.

2.4产蛋曲线拟合

根据淅川乌骨鸡产蛋性能测定数据，分别用伍德、杨宁和分室模型等3种数学模型对淅川乌骨鸡产蛋曲线进行非线性回归拟合，拟合的模型参数以及3种产蛋模型曲线与产蛋率实际观测曲线的比较分别见表5、图2.由表5可知，伍德模型拟合度较低，仅为0.674，而杨宁模型拟合度最高，达0.986，分室模型拟合度仅次于杨宁模型，为0.970.由图2可见，淅川乌骨鸡21～29周龄产蛋率迅速增长，达到高峰时产蛋曲线平滑下降.伍德模型曲线起始预测值大，增幅缓慢，后期下降较快，其预测的产蛋高峰在40周龄左右，和生产实际相比滞后，因此伍德模型不适合进行产蛋率曲线拟合；分室模型曲线预测值在产蛋初期与生产实际差异较大，但高峰过后曲线走势与实际生产曲线基本一致；杨宁模型曲线整体走势与实际观测曲线吻合度较高，只是在产蛋末期稍有偏差.因此，根据模型参数值、拟合度以及与实际观测值的相近程度等3项指标综合分析，杨宁模型是拟合淅川乌骨鸡产蛋曲线的最佳模型.

表4 淅川乌骨鸡产蛋性能

表5 产蛋率曲线模型参数及拟合度

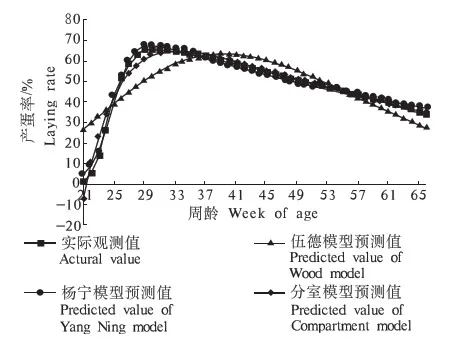
图2 淅川乌骨鸡产蛋模型曲线与实际观测曲线的比较

3 结论与讨论

家禽生长和产蛋曲线的拟合和分析是家禽育种和生产的基础工作，用理想的数学模型动态描述生长和产蛋随时间变化的规律对指导饲养管理和育种实践及控制家禽生长发育具有重要作用.目前禽类生长曲线的拟合，常用Gompertz，Logistic和Bertanlanffy模型.由模型拐点体重公式可知，Logistic模型拐点体重为A/2，即成熟体重的一半；Gompertz模型拐点体重为A/e，约为成熟体重的36.8%；Bertanlanffy模型拐点体重为8A/27，约为成熟体重的29.6%.当体重恒定时，3个模型到达拐点的时间先后顺序为Bertanlanffy

在众多拟合家禽产蛋率曲线的数学模型中，分室模型和杨宁模型由于各参数都具有相应的生物学定义而应用较为广泛.本研究用3种模型拟合淅川乌骨鸡产蛋曲线，发现伍德模型拟合度差，拟合后的模型预测值与实测值差异较大，并且其拟合的淅川乌骨鸡产蛋曲线与实际的产蛋率曲线有一定的滞后时间，这和MILLAN[9]、顾玉萍等[16]和史宪伟[20]的报道相一致.冯敏山等[21]拟合了从肉鸡单周和双周产蛋率曲线，认为分室模型最适合肉种鸡群产蛋曲线的拟合.本研究结果表明，杨宁模型的拟合效果最好，拟合度在0.986，其模型曲线与实际产蛋率曲线吻合度较高，这与顾玉萍等[16]对京海黄鸡的研究结果一致.但从模型参数a值上看，杨宁模型和分室模型的最大潜在产蛋率均超过了100%，与生产实际还存在较大差异.本研究结果表明，采用伍德、杨宁和分室模型等3种数学模型对淅川乌骨鸡产蛋曲线进行非线性回归拟合，根据模型参数值、拟合度以及与实际观测值的相近程度等3项指标综合分析，杨宁模型是拟合淅川乌骨鸡产蛋曲线的最佳模型.产蛋性状是受多基因调控的数量性状，在遗传和环境等内外因素的影响下不同品种鸡的产蛋量有很大差异，中国地方鸡种与国外高产品种相比，产蛋高峰期产蛋率不高，高峰过后产蛋曲线下降缓慢.总体上看，产蛋曲线不仅能反映出产蛋量的高低，还能将产蛋过程的特点以及群体的饲养管理状况等其它特点映射出来.

参考文献：

[1]LAIRD A K. Postnatal growth of birds and mammals[J]. Growth,1966,30:349-363.

[2]NELDER J A. The fitting of a generalization of the logistic curve[J]. Biometrics,1961,17:89-110.

[3]BERTALANFFY L. Quantitative laws in metabolism and growth[J]. Quarterly Review of Biollgy,1957,32:217-231.

[3]HANCOCK C E,BRADFORD G D,EMMANS G C,et al. The evaluation of the growth parameters of six strains of commercial broiler chickens[J]. British Poultry Science,1995,36:247-264.

[4]GOUS R M,MORAN E T J,STILBORN H R,et al. Evaluation of the parameters needed to describe the overall growth,the chemical growth,and the growth of feathers and breast muscles of broilers[J]. Poultry Science,1999,78:812-821.

[5]TZENG R Y,BECKER W A. Growth patterns of body and abdominal fat weights in male broiler chickens[J]. Poultry Science,1981,60:1101-1106.

[6]樊月钢,叶树真. 肉用仔鸡生长曲线的拟合及最大经济效益点的研究[J]. 中国畜牧杂志,1994,30 (3):30-31.

[7]张德祥,仇雪梅,杨 山,等. 不同性别肉仔鸡生长模式差异的研究[J]. 黑龙江八一农垦大学学报,1998,10(1):70-73.

[8]李世杰,赵月苹,江富华. 艾维茵肉仔鸡生长规律的模拟及最大经济效益点的研究[J]. 河北农业大学学报,1999,22(2):67-70.

[9]MILLAN I. Compartmental model analysis of poultry egg production curves[J]. Poultry Science,1981,60: 1549-1551.

[10]WOOD P D P. Algebraic model of the Lactation curve in cattle[J]. Nature,1967,216:164-165.

[11]YANG N,WU C,MILLAN I. New mathematical model of poultry egg production[J]. Poultry Science,1989,68(4):476-481.

[12]张学余,李国辉,苏一军,等. 苏禽乌骨鸡累计产蛋数曲线拟合和比较分析[J]. 河南农业科学,2011,40(10):134-136.

[13]殷建玫,李国辉,苏一军,等. 不同狼山鸡累积产蛋数曲线拟合和比较分析[J]. 江西农业学报,2012,24(2): 136-137.

[14]国家畜禽遗传资源委员会. 中国畜禽遗传资源志·家禽志[M]. 北京:中国农业出版社,2011.

[15]杜德英,吴蓉蓉,朱文奇,等. 文昌鸡生长曲线拟合的研究[J]. 家禽科学,2008(10):3-5.

[16]顾玉萍,侯启瑞,王金玉,等. 京海黄鸡生长和产蛋率曲线的拟合[J]. 中国家禽,2010,32(20):26-29.

[17]TZENG R Y,BECKER W A. Growth patterns of body and abdominal fat weights in male broiler chickens[J]. Poultry Science,1981,60:1101-1106.

[18]张 红,龚道清,张 军,等. 溧阳鸡生长曲线分析与拟合的研究[J]. 畜牧与兽医,2006,38(2):7-9.

[19]王存芳,张 劳,李俊英,等. 平原饲养的藏鸡体形外貌分析和生长模型拟合的研究[J]. 中国农业科学,2005,38(5):1065-1068.

[20]史宪伟. 蛋鸡产蛋曲线的数学模型研究[J]. 云南农业大学学报,1993,8(1):31-36.

[21]冯敏山,高山林,杨增芳,等. AA父母代肉鸡产蛋曲线的数学模型分析[J]. 中国家禽,2003,7(S1):20-21.