非线性铣削热传导逆问题的界面热流辨识*

冯 勇 汪木兰 王保升

(①南京工程学院机械工程学院，江苏南京 211167;②先进制造技术江苏省高校重点建设试验室，江苏 南京 211167)

高速切削工件时，由于切削速度快、时间短，热量在刀具、工件及空气中的传递形式主要为热传导。若在切削加工问题中已知工件的界面热流密度或者界面温度分布，就可以应用热传导方程来研究工件的温度分布状况，这一问题称为热传导正问题(DHCP:direct heat conduction problem)。但通常工件的界面热流或者界面温度分布无法直接通过在工件表面测量来获得。在这种情况下，需要由工件内部某些位置的温度值来反演出界面热流密度，这一问题称为热传导逆问题(IHCP:inverse heat conduction problem)［1］。

国内外学者对高速切削加工热传导问题开展了大量研究。Radulescu 和Kapoor 利用分离变量法建立了铣削中刀具温度的三维模型，并用解析法计算了热流量［2］;Lazoglu 利用有限差分法求解了切削热传导模型，计算了铣削加工过程中刀具和切屑的温度场［3］，M.R.Golbahar 通过对二维热传导逆问题的求解，对功能梯度材料的时变热流进行了分析预测［4］。山东大学张士军、刘战强采用热传导方法对涂层刀具的导热系数、热流量、切削温度场进行计算和有限元仿真［5］;安徽理工大学黄绍服、李君等人，采用热传导方法建立了高速铣削薄壁件温度场的数学模型［6］;重庆大学周忆、梁锡昌等人采用热源法和热传导法对超高速铣削加工中切削温度场进行建模［7］。而结合实测温度数据，考虑切削过程中温度叠加的非线性效应，采用优化算法对铣削加工中界面热流密度进行准确辨识的研究却极为少见。本文在建立铣削加工过程中工件的热传导数学模型基础上，采用PSO 算法，通过与工件内部的测量温度值的比较来确定被测工件的动态界面热流密度。由于该方法只需工件内部进行温度测量，不破坏被测工件的表面完整性，使得所计算出的界面条件比较准确，应用于热传导正问题的求解可以更准确得出工件的温度分布状况。

1 铣削热传导问题的数学描述

铣削加工是一个断续加工过程，刀具中每个切削刃都经历一个切入和切出的过程，切入工件时所产生的热量较小，将要切出时所产生的热量最大，切出后热源强度降为零。铣削加工中的移动热源形式可假设为三角形分布(图1 所示)，热流密度可表示为［8］:

n=0，1，2，...，t 为加工周期;t1为刀具切入时间。

采用热传导法求解工件在切削区的温度场分布问题可抽象成二维传热问题，所建立的铣削加工过程如图2 所示(图中n 为主轴转速;aw为径向切削深度;R 为刀具半径)。此时，工件固定不动，刀具以主轴转速n 旋转并以进给速度vf沿X 方向前进，忽略材料塑性变形所产生的热量，并假定工件的比热、密度以及热传导系数为常数，对于干切削过程，铣削面与空气的对流换热系数比较小，工件表面可看成绝热边界。根据热力学第一定律，可得铣削加工的导热微分方程为［9］:

式中:T 为工件上任一点的温度，℃;k 为工件的热传导系数，W/(m·℃);ρ 为工件的密度，kg/m3;c 为比热容，J/(kg·℃);vf为刀具沿x 方向的进给速度，m/s;τ为切削时间，s。给定边界条件、初始条件分别如式(3)所示:

式中:q 为热流密度，W/(m2℃);R 为刀具半径，m;T0为初始时刻工件温度，℃。若给定q 及T0的值来求解上述问题，称之为热传导正问题。若通过某些点的温度测量值来求得T，则称之为热传导逆问题。

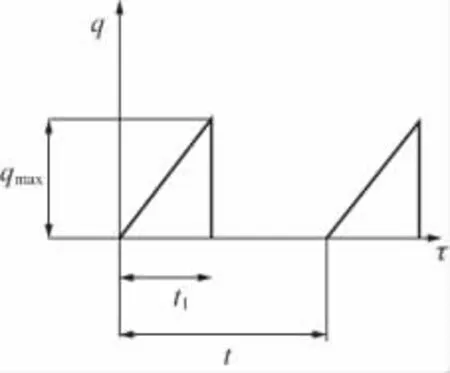
图1 铣削加工中的移动热源形式

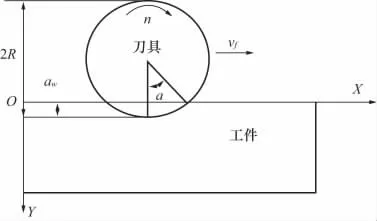
图2 铣削加工工作示意图

求解热传导逆问题一般采用数值计算，近年来研究发现人工智能中的一些算法可以较好地应用于该问题的求解，常见的方法有启发式算法和非启发式算法。启发式算法具有收敛速度快的优点，但是不能保证全局收敛，使得问题陷入局部最小值，得不到最优解。非启发式算法包括蚁群算法、模拟退火算法、PSO 算法等，这些算法通过设置一定的约束条件，既可在求解空间内找到全局最优解又可保证求解精度［10］。

2 基于PSO 算法的热流密度辨识方法

2.1 辨识原理

采用PSO 算法开展铣削加工的动态热流密度辨识研究的流程图如图3 所示，其基本分析步骤如下:

(1)测出工件内部某一位置处的切削温度T(t)随时间变化曲线，并设定界面热流的初值q0。

(2)应用热传导正问题求解方法得出工件任一位置的温度分布情况及工件内部A 位置处的温度场T0(t)。

(3)由于热流密度初值并不准确，因此T(t)与T0(t)存在着一定误差，实际问题中，为提高求解精度往往采用测量多个点的温度来评定综合偏差，其表达式如式(4)所示。

(4)按照PSO 算法的求解思路，通过使不同时刻的综合偏差达到预定的极小值，即可求得动态的热流密度变化曲线。

图3 辨识方法流程图

2.2 算例计算

为验证上述算法的可行性，并进一步研究不同参数及惯性权重值对寻优效果的影响，对式(5)所给定的算例开展热流密度辨识研究。

该算例中热流密度q 未知，其他参数为已知:热传导系数k=47.7 W/(m ·K)，热扩散率α=0.082 34 cm2/s，对流换热系数h=20 W/(m2℃)，x1=0.016 m，δ=0.03 m。将上述热传导逆问题求解转化为关于综合偏差的优化问题，选取测量点位置的坐标值分别为:x=1、3、5、7、9 mm，y=2、4 mm，总计10 个位置点，粒子的适应度方程如式(6)所示。求解过程中设定粒子群的总数为50，待求热流密度的搜索范围为(100 000，1 000 000)，速度系数取为0.1。随机参数r1和r2为［0，1］间的随机数，学习因子c1和c2取为2。最大搜索次数为100;最优适应值小于100;初始权重为0.9，最终权重为0.4。

表1 t=1 s 粒子的最优适应值的变化

首先，假定t=1 s 时刻的真实热流密度q=335 200 W/(m2℃)，通过算例所给出的热传导模型，计算t=1 s 时刻10 个被测点的温度值，…，作为真实参考温度;其次，任选一个热流密度值代入到热传导数学模型中，求得被测点温度的计算值为T1，T2，…，T10;最后，按照上述热流密度辨识方法的步骤对该问题进行优化运算。计算过程中，粒子最优位置的适应值变化情况如下表1 所示，从表中可以看出，随着搜索次数的增加，粒子群最优位置的适应值逐渐下降，热流密度的计算值与实际值之间的误差越来越小，在粒子的迭代次数超过60 以后，粒子的最优适应值满足要求。

图4 不同测点个数n 计算得的热流相对误差曲线

图4 为选取测量点个数为10 和20 时，热流的相对偏差变化曲线，从中可以看出当选测点个数n=20时的相对误差比n=10 时小，迭代效果更好且粒子的收敛能力也很好。因此，在条件允许的情况下，选择更多的测量点能够减小迭代过程中粒子最优位置与目标位置间的偏差量。

3 铣削温度测量

图5 测温实验原理

3.1 实验原理

待测点温度测量装置原理如图5 所示，系统的坐标原点位于图示工件的右顶端线的中心位置，X、Z 轴方向如图所示，Y 轴由右手法则确定。将工件剖分成两块，工件剖面处粘贴绝缘片(云母片)，将标准热电偶置于剖分后的工件之间，并使其略低于工件顶面1.0 mm 左右，然后将两块工件在工作台上对齐夹紧。切削过程中，当热电偶节点感受到被测点温度时毫伏计输出相应的电压值，通过比对电压值与温度的关系曲线就可以获得工件上任意位置点的温度变化曲线［11-12］。实验中选用镍铬-镍硅组成的K 型标准热电偶，该热电偶具有测量范围广(0～1 300 ℃)、反应灵敏、精度高等特点。

3.2 实验系统构建

3.2.1 试验条件

(1)机床:立式加工中心，型号MCV850。

(2)工件材料及刀具:工件采用AISI1045 钢;试件的规格为80 mm×80 mm×30 mm;刀具采用硬质合金双刃铣刀，直径为12 mm。

(3)测试装置:由热电偶回路、信号放大装置、采集卡、计算机所组成，应用MFC AppWizrd 建立基于对话框的数据采集界面，采样频率为6 000 Hz，最终测试装置如图6 所示。K 型标准热电偶选用直径1 mm。

(4)环境温度:10 ℃。

3.2.2 实验方案

主轴转速为3 000 r/min，轴向切削深度为1.5 mm，进给速度为100 mm/min;铣削方式:顺铣干式切削;环境温度:10 ℃;被检测点位置的横坐标分别为4、5、6、8、9、10、12、15、20、25，纵坐标分别为0、5，共计20个坐标位置。

图6 温度采集系统

4 铣削热流密度辨识

采用前述算例分析中的计算参数，在所建立的铣削热传导模型基础上，按照PSO 算法的求解思路，将该热传导逆问题的求解转化为误差的优化问题。计算分析所选用工件和刀具材料的物理参数如表2 所示。

表2 工件和刀具的材料参数

为研究铣削加工过程中的动态温度分布情况，必须计算不同时刻的界面热流值。为此，结合20 个被测点的动态温度变化曲线，对不同离散时刻的热流值开展求解。表3 所示为不同时刻粒子的最优位置适应值，从表中可以看出，粒子群最优位置的适应值最大为65.6385，满足偏差分析要求。将上述离散时刻的热流密度值按照时间变化绘制成热流曲线，如图11 所示。由曲线可以看出，铣削加工中不同时刻的热流呈明显的非线性变化，全局最大热流密度与最小热流密度值分别为2.856 ×106和2.823 ×106W/(m2·℃)，分别出现在5 s 和10 s 左右。此外，从整个热流变化曲线来看，在加工的前期(0～10s)，界面热流先发生了急剧的增大，而后发生了骤降;在加工的中期(10～35 s)，界面热流趋于稳定变化阶段;而在加工的后期(35～48 s)，界面热流又发生了类似于加工前期的变化情形。上述变化趋势表明界面热流受到物理边界的影响较大。

表3 典型时刻粒子的全局最优适应度

图7 界面热流变化曲线

5 结语

本文基于高速铣削机理分析，建立了热传导逆问题求解的优化模型，阐述了应用PSO 算法求解热传导逆问题的求解流程，并通过所述热流密度辨识方法，结合实验数据对AISI 1045 钢在铣削过程中的热流密度变化情况进行了分析。分析结果基本满足了铣削加工热传导问题求解的误差要求，为准确研究铣削加工的温度分布提供了理论依据。

(1)单次切削过程中，界面热流分布呈非线性变化，全局最大热流与最小热流值分别为2.856 ×106和2.823 ×106W/(m2·℃)。

(2)整个优化过程中，粒子群最优位置的适应值最大为65.638 5，界面热流的计算值与实际值之间的偏差仅为2.635%，满足了铣削加工热传导问题求解的误差要求。

(3)从整个加工过程的界面热流变化曲线分析来看，界面热流的变化存在3 个典型阶段，其中前期、后期两个阶段的界面热流变化比较显著，受边界条件的影响较大。

［1］钱炜祺，周宇，何开锋，等.非线性热传导逆问题的表面热流辨识方法［J］.空气动力学报，2012，30(2):145 -150.

［2］Radulescu R，Kapoor S G.An analytical model for prediction of tool temperature fields during continuous and interrupted cutting［J］.Journal of Engineering for industry，1994，116:135 -143.

［3］Ismail Lazoglu，Yusuf Altintas.Prediction of tool and chip temperature in continuous and interrupted machining ［J］.International Journal of Machine Tools ＆ Manufacture，2002，42(9):1011 -1022.

［4］Haghighi M R G，Eghtesad M，Malekzadeh P，et al.Two -dimensional inverse heat transfer analysis of functionally graded materials in estimating time -dependent surface heat flux［J］.Numerical Heat Transfer，2008，54:744 -762.

［5］张士军.涂层刀具切削温度及其测试技术研究［D］.山东:山东大学，2009.

［6］黄绍服，李君，何庆，等.薄壁件高速铣削温度场研究［J］.安徽理工大学学报:自然科学版，2006，26(1):14 -17.

［7］周忆，梁锡昌，陈斌.超高速铣削加工的温度场计算及生产应用［J］.中国机械工程，2003，14(13):1158 -1161.

［8］范晶晶.高速加工切削温度软测量技术及其试验系统［D］.常州:常州大学，2013.

［9］陈明，袁人炜，凡孝勇，等.三维有限元分析在高速铣削温度研究中的应用［J］.机械工程学报，2002，38(7):155 -161.

［10］钱炜祺，何开锋，桂业伟，等.非稳态表面热流反演算法研究［J］.空气动力学学报，2010，28(2):155 -161.

［11］冯勇，汪木兰，王保升.高速切削热及温度预测研究进展［J］.机械设计与制造，2012，255(5):266 -268.

［12］Feng Yong，Wang Mulan，Wang Baosheng，et al.Influence of the process variables on the temperature distribution in AISI 1045 turning proceedings［A］.Advanced Materials Research，2012，578:1364-1368.