高超声速激波/边界层干扰流动数值模拟研究

龚安龙，刘 周，杨云军，周伟江

(中国航天空气动力技术研究院，北京 100074)

0 引言

近年来，全世界范围内掀起了高超声速飞行器研制的热潮，其中高超声速流动中激波/边界层干扰现象的准确预测成为亟待解决的空气动力学难题。高超声速双锥分离流动是一类典型的激波/边界层干扰流动。其流动现象广泛存在于高超声速飞行器气动控制面、局部凸起物等与飞行器本体形成的气流压缩区域，可能带来极其严重的气动力、热问题。高超声速双锥流动已经得到了广泛的实验和数值模拟研究，并成为CFD代码确认的重要算例。Holden等人［1-4］开展了双锥高超声速流动的系列实验研究，获得了多个状态下准确的流动特性和压力、热流分布数据。在数值模拟方面，Candler、Roy、Gnoffo、Nompelis 等人［5-24］做出了很多贡献，他们研究了高温真实气体效应以及稀薄气体效应对风洞来流条件和双锥壁面流动特性的影响，也研究了网格收敛性、数值格式等方面对分离流动模拟可靠性的影响情况。本文在基于Roe格式的全 Navier-Stokes方程计算流体力学(CFD)代码基础上引入了一种局部熵修正方法，用于进行双锥高超声速分离流动的模拟验证，并分析了网格和熵修正方法耗散性对流动模拟准确性的影响特性。

1 双锥模型及来流条件

双锥模型来源于Holden等人的高超声速实验，这里选用了尖头的前锥25°和后锥55°模型，如图1所示。Holden等人通过多个状态的实验，详细研究了高超声速双锥流动的机理，建立了其流动结构。如图2所示，双锥高超声速流动包含了前锥上激波与粘性分离流动的相互干扰、两个锥面上激波的相互干扰以及由此形成的输运激波侵入第二锥底层流动等复杂的流动结构。两锥之间形成的分离区大小、输运激波侵入位置及当地的压力与热流分布等跟来流的条件非常敏感。本文选用了两个典型来流状态——Run 28和 Run 35——进行研究，来源于 holden等人［3-4］的实验，见表1。

表1 双锥流动的风洞实验来流条件Table 1 Flow conditions of double-cone experiment in wind tunnel

2 网格生成

复杂的高超声速双锥分离流动对于CFD数值模拟来说极具挑战性，其中一个重要原因就是计算结果的网格敏感性非常强［7-9］，即网格达到极密的情况下才能得到满足网格收敛性条件的流场解，甚至对于某些数值方法无法达到网格收敛性。本文采用了三套由稀到密的网格(二维轴对称网格)用以考察网格的收敛性:(1)coarse——稀网格300×100(流向×法向，下同);(2)medium——中等网格 600×200;(3)fine——密网格1200×400。图3显示了中等网格规模的网格分布情况，在前锥和两锥的压缩拐角处网格进行了加密处理以保证分离区流动的精细捕捉。

图1 尖双锥实验模型尺寸图Fig.1 Size of the double-cone experimental model

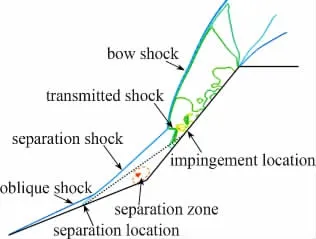
图2 高超声速尖双锥分离流动结构示意图Fig.2 Diagrammatic sketch of the hypersonic sharp double-cone separated flow

图3 CFD数值模拟采用的中等规模网格(600×200)Fig.3 Medium grid adopted in CFD numerical simulations(600×200)

3 数值计算方法简介

本文采用的CFD数值计算方法［25］以可压缩全Navier-Stokes方程为控制方程;空间离散采用有限体积方法，无粘通量采用Roe格式;时间推进采用隐式SGS方法;定常解获得的定义为在典型位置(分离点和再附点附近等)的物面监控点和分离区流场参数不再发生改变为止。由于所研究的风洞实验条件为层流状态，因此CFD数值模拟中粘性流动采用层流处理。

对于Roe格式，在高超声速流动计算中需要引入熵修正来抑制红玉(Carbuncle)现象和保证计算的稳定性。但是通常采用的熵修正方法在空间是各项同性的，并且在全部计算单元都是同一个值，这样就会在弱梯度方向和粘性主控流动区域产生多余甚至错误的耗散。多余的耗散将改变分离区流动特性，从而使得粘性摩擦力和热流计算结果出现异常。为此，本文引入了一种局部熵修正方法［26］，用于克服常规全局熵修正的不足。该局部熵修正方法采用基于压力的辅助限制器。对于通量Jacobian矩阵的每一个特征值λ，需要由最小特征值λmin来限定，即:

其中λmin是当地流场参数的函数，表示为:

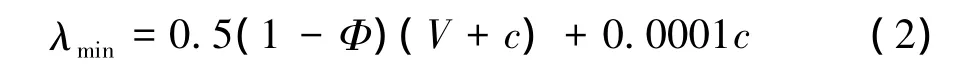
其中V和c分别是当地单元的速度和声速，Φ是当地计算单元所有面上的压力比值的函数［26］。

该局部熵修正方法在捕捉强激波间断(单元面上的压力值存在较大的跳跃)时能够有效的抑制红玉现象发生，而在其它弱压力梯度的流动区域(如粘性边界层流动区域等)不引入熵修正，即不产生多余耗散，很好的克服了全局熵修正方法的弊端。

4 模拟结果与讨论

4.1 网格敏感性分析

对于Run 28实验状态，采用三套不同密度的网格进行了计算。图4给出了不同密度网格下计算获得的激波边界线的分布情况比较，可以看到:网格过稀会导致计算的分离区减小;中等网格与密网格计算结果已经非常吻合。图5进一步比较了压力系数和反映热流的Stanton数沿流向的分布情况，不难发现:稀网格计算的流动分离区小，而压力和热流峰值高;中等网格已经非常接近密网格计算结果，即已经满足网格收敛性。

图4 不同网格密度下计算获得的激波位置(Run 28)Fig.4 Results of shock position from different grid levels(Run 28)

图5 不同网格密度下压力系数和Stanton数计算结果(Run 28)Fig.5 Results of pressure coefficient and Stanton number from different grid levels(Run 28)

4.2 熵修正方法耗散性影响分析

为考察本文引入的局部熵修正方法是否有效，这里比较分析了全局和局部熵修正方法在不同修正系数(反映修正强弱程度)下计算得到的压力和热流参数，如图6所示。采用全局熵修正方法，选用较大的修正系数将带来很大的耗散，从而导致计算的分离区偏小;而如果选用较小的修正系数，则很容易出现红玉现象和计算的不稳定。而采用局部熵修正方法，选用不同的修正系数计算获得的分离区大小几乎没有差异，但较大的修正系数能够很好的抑制红玉现象。

4.3 与实验结果的比较与分析

为了进一步验证本文计算方法和结果的可靠性，将局部熵修正方法计算的结果与Holden的实验结果以及Candler［5-8］采用全局熵修正方法计算得到的结果进行了比较。两种实验条件下的计算和测量获得的压力系数和Stanton数沿流向的分布曲线见图7和图8。通过比较发现，两种计算方法获得的流动分离区相差不大，均与实验结果比较吻合;而采用局部熵修正方法获得的压力系数和Stanton数的分布及其峰值与实验结果更加一致。

图6 不同熵修正方法的压力系数和Stanton数计算结果(Run 28)Fig.6 Results of pressure coefficient and Stanton number from different entropy fix methods(Run 28)

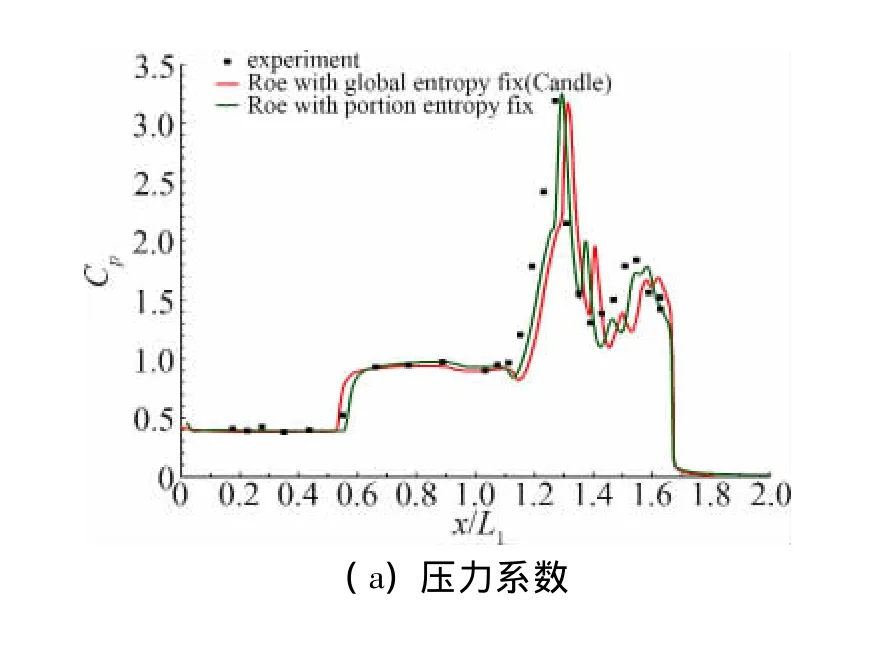
图7 计算结果与实验结果的比较(Run 28)Fig.7 Results comparison between computation and experiment(Run 28)

图8 计算结果与实验结果的比较(Run 35)Fig.8 Results comparison between computation and experiment(Run 35)

5 结论

本文采用基于全Navier-Stokes方程的CFD数值模拟技术研究了一类典型的高超声速激波/边界层干扰流动——双锥分离流动。通过研究数值预测结果的网格敏感性、熵修方法耗散性影响等，获得如下一些结论:

(1)激波干扰下的分离流动特性及流场物理参数对计算网格比较敏感，过稀的网格将导致分离区减小，压力和热流峰值增大，本文采用的中等网格已经达到网格收敛性要求;

(2)在Roe格式中引入局部熵修正方法，既能够有效的抑制红玉现象，也保证在弱压力梯度的粘性层不引入多余耗散，是一种能够更加准确模拟复杂高超声速激波/边界层干扰流动的方法。

［1］HOLDEN M S.Shock interaction phenomena in hypersonic flows［R］.AIAA Paper 98-2751，1998.

［2］HOLDEN M S.Experimental studies of laminar separated flows induced by shock wave/boundary layer and shock/shock interaction in hypersonic flows for CFD validationp［R］.AIAA Paper 2000-0930，2000.

［3］HOLDEN M S，WADHAMS T P.Code validation study of laminar shock/boundary layer and shock/shock interactions in hypersonic flows.part A:experimental measurements［R］.AIAA Paper2001-1031，2001.

［4］HOLDEN M S.Experimental studies in LENS shock and expansion tunnel to examine real-gas effects in hypervelocity flows［R］.AIAA Paper 2004-0916，2004.

［5］OLEJNICZAK J，CANDLER G V，HORMUNG H G.Computation of double-cone experiments in high enthalpy nitrogen［R］.AIAA Paper 97-2549，1997.

［6］WRIGHT M J，SINHA K，OLEJNICZAK J，et al.Numerical and experimental investigation of double-cone shock interactions［J］.AIAA Journal，2000，38(12):2268-2276.

［7］CANDLER G V，NOMPELIS I，HOLDEN M S.Computational analysis of hypersonic laminar viscous-inviscid interactions［R］.AIAA Paper 2000-0532，2000.

［8］CANDLER G V，NOMPELIS I，DRUGUET M C.Navier-Stokes predictions of hypersonic double-cone and cylinder-flare flow fields［R］.AIAA Paper 2000-1024，2000.

［9］ROY C J，GALLIS M A，BARTEL T J，et al.Navier-Stokes and direct simulation monte carlo predictions for laminar hypersonic separation［R］.AIAA Paper 2001-1024，2001.

［10］GNOFFO P A.CFD Validation studies for hypersonic flow prediction［R］.AIAA Paper 2001-1025，2001.

［11］CANDLER G V，NOMPELIS I.CFD validation for hypersonic flight:real gas effects［R］.AIAA Paper 2002-0434，2002.

［12］CANDLER G V，NOMPELIS I，DRUGUET M C，et al.CFD validation for hypersonic flight:hypersonic double-cone flow simulations［R］.AIAA Paper 2002-0581，2002.

［12］ROY C J，GALLIS M A，BARTEL T J，et al.Navier-Stokes and DSMC simulations for hypersonic laminar shock-shock interaction flows［R］.AIAA Paper 2002-0737，2002.

［13］DRUGUET M C，CANDLER G V，NOMPELIS I.Simulations of viscous hypersonic double-cone flows:influence of numerics［R］.AIAA Paper 2003-3548，2003.

［14］NOMPELIS I，CANDLER G V，HOLDEN M S，et al.Computational investigation of hypersonic viscous/inviscid interactions in high enthalpy flows［R］.AIAA Paper 2003-3642，2003.

［15］WADHAMS T P，HOLDEN M S.Experimental studies and numerical predictions for hypervelocity vehicle design and code validation［R］.AIAA Paper 2003-6905，2003.

［16］NOMPELIS I，CANDLER G V，MACLEAN M，et al.Numerical investigation of high enthalpy chemistry on hypersonic double-cone experiments［R］.AIAA Paper 2005-0584，2005.

［17］DRUGUET M C，CANDLER G V，NOMPELIS I.Effect of numerics on Navier-Stokes computations of hypersonic double-cone flows［J］.AIAA Journal，2005，43(3):616-623.

［18］NOMPELIS I，CANDLER G V，MACLEAN M，etal.Numerical investigation of double-cone flow experiments with high-enthalpy effects［R］.AIAA Paper 2010-1283，2010.

［19］NOMPELIS I，CANDLER G V，HOLDEN M S，et al.Real gas effects on hypersonic shock wave laminar boundary layer interactions［R］.AIAA Paper 2003-0443，2003.

［20］NOMPELIS I，CANDLER G V，HOLDEN M S.Effect of vibrational nonequilibrium on hypersonic double-cone experiments［J］.AIAA Journal，2003，41(11):2162-2169.

［22］NOMPELIS I，CANDLER G V，WADHAMS T P，et al.Numerical simulation of high-enthalpy experiments in the LENS-X expansion tube facility［R］.AIAA Paper 2004-1000，2004.

［23］MACLEAN M，CANDLER G V，HOLDEN M S.Numerical evaluation of flow conditions in the LENS reflected shock-tunnel facilities［R］.AIAA Paper 2005-0903，2005.

［24］MACLEAN M，HOLDEN M S，WADHAMS T P，etal.A computational analysis of thermochemical studies in the LENS facilities［R］.AIAA Paper 2007-0121，2007.

［25］LIU Z.Delayed detached eddy simulation for static and forced oscillating airfoil at high angle of attack［R］.IAC 2013，2013.

［26］GNOFFO P A.Updates to multi-dimensional flux reconstruction for hypersonic simulations on tetrahedral grids［R］.AIAA Paper2010-1271，2010.