基于自适应遗传算法的配电网DG选址与定容

张 力，郑 立，张 尧

（1.吉林省电力勘测设计院，长春 130022；2.华南理工大学电力学院，广州 510641）

随着分布式电源（DG）越来越多的接入配电网，使配电网由一个无源网络变为有源网络，合理地对DG进行选址和定容显得尤为重要，由此衍生出诸如电能质量、供电可靠性、安全性、经济性等与配电网相关的供电问题［1-2］。分布式电源选址与定容属于多变量最优化求解问题，国内外已有众多学者对此进行了研究。文献［3］在已知分布式电源总容量的情况下，以实现最小配电网网损为目标，采用禁忌搜索法对分布式电源的位置和容量进行分解协调。文献［4］以利益／成本比为目标函数，利用遗传算法对分布式电源的位置和容量进行了优化。文献［5］提出了一种配电网扩展规划中进行DG选址定容的方法，但未考虑算法的收敛性能和搜索能力，容易陷入局部最优解。

本文在DG数量、位置和单个电源容量均不确定的情况下，首先采用前推回代法进行含DG的配电网潮流计算，其次建立了以折算到每年的DG的投资运行费用、线路运行费用及引入DG后购电费用最小为目标函数的配电网规划经济模型，最后应用自适应遗传算法对DG进行优化配置，并得到DG的优化配置方案。

1 计及DG的配电网潮流计算

图1所示为一条典型的配电网辐射状线路，在负荷节点i上安装有DG。根据配电网络的特点，国内外学者研究了多种潮流计算方法，各有特点和求解范围。本文中配电网潮流的求解方法依然采用传统的配电网潮流求解方法，即常用的推回代法进行计及DG的配电网潮流计算。辐射线路中的潮流可采用如下方程描述［6］：

图1 含分布式电源的配电网单辐射线路

式中：PLi、QLi分别为第i个节点上消耗的有功功率和无功功率；PLn、QLn分别为第n个节点上消耗的有功功率和无功功率；PDGi，QDGi分别为第i个节点上装设的DG所发出的有功功率和无功功率；Ui－1，Pi－1分别为第i－1个节点上的节点电压和注入有功；Ri－1，Xi－1分别为第i－1节点和i节点之间的线路电阻和电抗，i＝1，2，……，n。

2 计及DG的配电网规划经济性模型

配电网规划的目的是根据电源发展及负荷的增长情况，合理地确定若干年后的目标网络结构；而通过合理的接入DG，可以在不改变或最小限度改变网架结构的情况下，满足负荷的增长，并使配电系统的建设和运行费用最小。

本文依据配电网规划经济模型，建立了以折算到每年的DG的投资运行费用、线路运行费用及引入DG后购电费用最小为目标的函数［7］。由于当前我国尚不存在大规模的用户侧直接投资安装分布式电源情况，对于少数用户投资安装的分布式电源来说，容量较小，且国家财政予以一定补贴，因此不存在经济性问题。故本文只考虑由电网公司作为分布式电源投资者这一简化模型进行经济性分析。

2.1 目标函数

2.2 不等式约束条件

式中：Ui和IL分别为节点电压和支路电流，它们应分别满足节点电压约束和支路最大电流约束；PDGi和SDGi分别为节点i所装DG注入的有功功率以及DG接入容量，本文对DG出力进行了约束，即DG在配电网中接入容量应满足DG出力的上下限且总接入容量不超过电网最大负荷总量的10%；SL为电网负荷总量的10%。

2.3 等式约束条件

等式约束条件即为配网潮流求解方程，如式（1）至（3）所示。

2.4 归一化目标函数

将所有不等式约束条件以惩罚因子的形式并入归一化目标函数，所得新目标函数为：

式中：KU为节点电压越限惩罚因子；KI为支路电流越限惩罚因子；K∑DG为DG容量越限惩罚因子；IJ为相邻支路电流。

3 自适应算法求解流程

由于标准遗传算法自身固有的缺陷，通常计算过程中收敛速度慢，全局搜索能力差，易陷入局部最优解而导致早熟现象［8］。针对这些问题，本文采用自适应遗传算法，使得交叉算子Pc和变异算子Pm能够随适应度自动改变，避免了上述缺陷。

3.1 编码格式

本文对DG的位置和容量变量采用实数编码的方法，用一组变量C＝｛Cl，C2，…，Ci，…Cn｝来表示，Ci的数值说明了对应的负荷节点i分布式电源的建设情况：若Ci＝0则说明该负荷节点i没有DG；若Ci＝1则表示该负荷节点建有DG，且安装容量为100kVA；若Ci＝2则表示该负荷节点上DG按照容量为200kVA，依此类推。

3.2 自适应函数

交叉概率Pc和变异概率Pm的选择是影响遗传算法行为和性能的关键所在，直接影响算法的收敛性。本文采用自适应调制的交叉和变异算子，对于适应值高于群体平均适应值的个体，采用较低的Pc和Pm，来保存优良个体进入下一代；而低于平均适应值的个体，采用较高的Pc和Pm，使该解被淘汰掉，因此，自适应的Pc和Pm能够提供相对最优解，改进了全局收敛能力和搜索能力，有效地提高了遗传算法的优化能力。

在自适应遗传算法中，交叉率和变异率按如下公式进行自适应调整［9］：

式中：fmax代表群体中最大的适应度值；favg代表每代群体的评价适应度值；f′代表要交叉的两个个体中较大的适应度值；f代表要变异个体的适应度值。

算法求解流程见图2。

4 算例分析

本文选取某地24节点10kV低压配电网为算例（见图3），对所提出算法的有效性行验证。模型参数如下：网络中负荷节点7～24均可运行安装DG，且假设DG直接安装于负荷节点上。待选单个DG功率因数η＝0.9，容量为100kVA的整数倍，且不大于所安装节点的负荷量。算法参数依照文献［10］设定：群体大小 M＝60，Pc1＝0.9，Pc2＝0.4，Pm1＝0.100，Pm2＝0.001，最优保存数量取2，最优解不变最大代数Gmax＝5，最大迭代次数Nc＝50，收敛判据ε＝0.0001。

针对算例本文仅考虑光伏发电的年最大负荷利用时间，取τmaxi＝3000h；单位电价Cpu＝0.5元／（kW·h），惩罚系数KU＝KI＝K∑DG＝100，DG的固定投资年平均费用系数为0.35。

表1为遗传搜索中止时最优的DG位置和容量方案。其位置编号表示DG的接入节点，容量编号表示DG的接入容量，其基准单位是100kVA。

图2 自适应遗传算法求解流程

图3 某城市24节点10 kV配电网网架

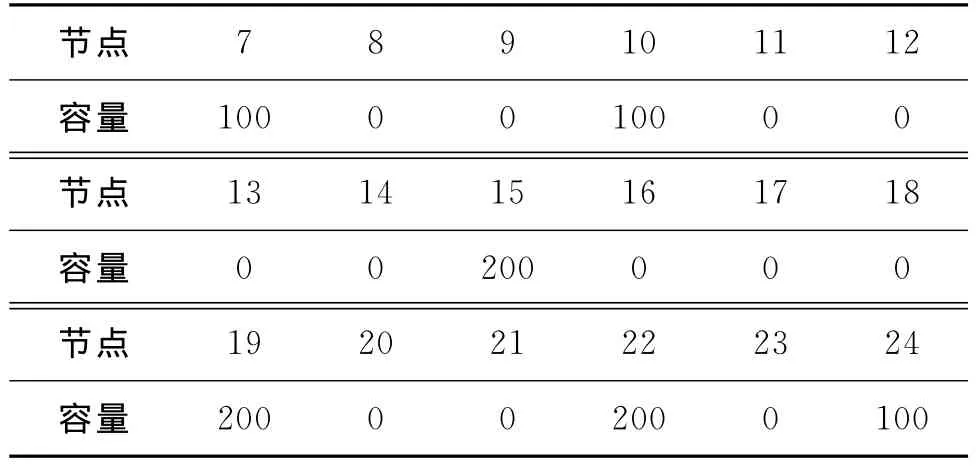
表1 DG最优安装位置和容量 kVA

表2为算例总运行费用结果。从表2可以看出，在配电网负荷节点处接入DG后，可起到延缓相关线路升级的作用，从而降低线路维护这块的费用支出；同时DG可在一定程度上减轻线路负载状况原因，使得潮流有功功率网损这一块的费用支出同样显著降低（从表2可见网损大幅下降了约24.4%），从而在整体上获得了较高的收益和性价比，总运行费用较未引入DG前下降了13.69%，即节省了52.064万元，可见在配电网中对DG进行合理的选址定容能对配电网规划产生客观的经济效益。

表2 算例总运行费用结果 万元

同时从表2可以看出，DG总运行费用在总费用中所占比例偏高，这是由于目前DG的发电成本较高。随着科技的发展，DG的建设成本会越来越低，含DG的配电网规划方案的经济优势会越来越明显。

图4为本文DG选址定容所采用算法的迭代收敛过程。算法收敛曲线在迭代137次后逐渐趋于平稳，并向全局最优解慢慢靠拢。该图表明本文所采用的“改进的自适应遗传算法”在求解配电网中DG的选址定容问题时是可行的。

图4 改进的自适应遗传算法收敛曲线

5 结束语

本文采用了自适应遗传算法对配电网中DG的位置和容量进行优化配置。通过对某地24节点10 kV低压配电网算例分析，验证了本文所采用算及所建立分布式电源选址定容数学模型的正确性和有效性。仿真结果表明，合理地对DG接入配电网的容量和位置进行规划，能够在降低线路损耗的同时，为配网系统整体运行创造经济价值。

［1］梁才浩，段献忠.分布式发电及其对电力系统的影响.电力系统自动化，2001，25（12）：53－56.

［2］梁有伟，胡志坚.分布式发电及其在电力系统中的应用研究综述［J］.电网技术，2003，27（12）：71－75.

［3］夏澎，周明.分布式电源选址定容的多目标优化算法［J］.电网技术，2011，35（9）：116－121.

［4］海晓涛，徐岩.基于免疫遗传算法的智能配电网分布式电源选址定容［J］.研究与分析，2011，18（7）：58－61.

［5］王成山，陈恺，谢莹华，等.配电网扩展规划中分布式电源的选址和定容［J］.电力系统自动化，2006，30（3）：38－43.

［6］鲁跃峰，李海涛，周巍，等.含分布式电源的配电网改进快速解耦法潮流计算［J］.广东电力，2013，26（3）：56－61.

［7］余健明，吴海峰，杨文宇.基于改进多种群遗传算法的配电网规划［J］.电网技术，2005，29（7）：36－40.

［8］徐赫，李欣，汪海.基于改进遗传算法的配电网网架规划［J］.广东电力，2010，23（6）：6－9.

［9］段玉倩，贺家李.遗传算法及其改进［J］.电力系统及其自动化学报，1998，10（l）：39－52.

［10］蔡丽霞.含分布式电源的配电网规划研究［D］.山东：山东大学，2009.