风储联合系统的输电规划研究

刘姝婷，王 尧，赵 晨，赵 莹

(1.国网太原供电公司，太原 030000;2.华北电力大学，北京 102206;3.国网山西省电力有限公司，太原 030000;4.重庆电力高等专科学校，重庆 400053)

风力发电随机性、波动性的特点［1］及储能设备的技术突破，使大规模储能设备投入电网成为可能。储能设备不仅能充分利用风能以最大限度地发挥风机效能，而且平抑了风电出力波动，提高电能质量［2］;对比降额输出方式减少了弃风量，提高风电场效益;使电网运行方式减少，投资成本降低。在全球能源紧张的背景下，大规模储能设备的应用成为未来电网发展的必然趋势。

国内外学者已经开始着手研究风电场给电网带来的一系列不确定问题，但对于风储联合系统的输电规划研究还很欠缺。文献［3］利用储能容量成本及风电场输出功率平滑效果辅助判据，得出风电场储能容量合理的取值范围。文献［4］提出了一种基于功率预测和储能系统配合的风电场功率波动平抑方法，分析了风电场日出力曲线与储能容量关系，得到风电场合理的储能容量。文献［5］将风电场出力和负荷变动分为多个场景，根据每个场景发生的概率得到输电网在不同场景下的最优规划结果。文献［6］根据历史或预测数据，将风电场出力分段线性化，建立含风电场的输电网规划模型，既考虑风电波动性又不会增加模型复杂度。

本文主要研究风储联合系统采用跟踪计划控制策略下的满足电网及风电场需求的储能设备最优容量，作为输电网规划的基础。根据历史或预测数据，对风电场出力进行分段线性化处理，电网中其他火电机组按照最优经济调度原则配合风电场出力，建立以全网效益最大化为目标的输电网规划模型。在求解模型阶段，采用风电场典型日出力曲线及改进IEEE-18节点系统，利用人工鱼群算法对所建模型求解，分别得到1、2、4、8分段对应的储能设备最优容量和输电网规划方案。通过比较各分段系统费用情况可知，电网中投入储能设备且按一定方式运行能够有效减少输电网投资，提高系统的经济性，具有可行性。

1 风力发电数学模型

风能具有间歇性、随机性、波动性，给系统带来了一系列的不确定性因素。风力发电场输出功率数学模型的建立有间接法和直接法两种。

1.1 间接法

以研究地区的风速时间序列为基础，根据风速与风电场出力的函数关系，间接算出风电场的输出功率。风电场出力与风速关系函数由如下函数表示:

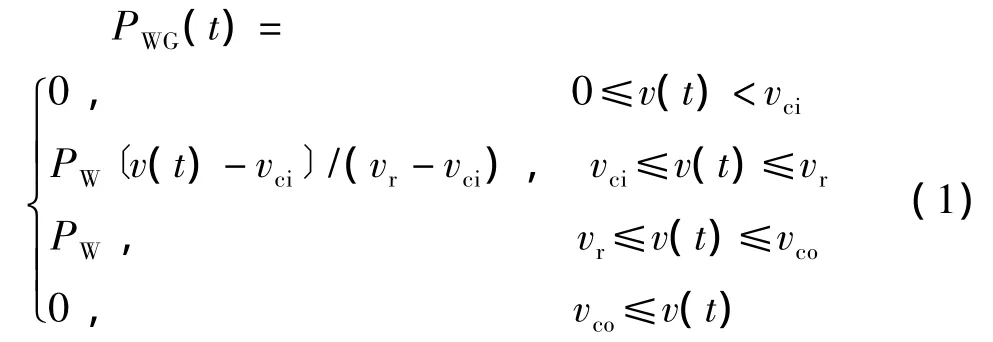
式中:PWG(t)为风电输出功率;PW为风电机组的额定容量;vci、vco、vr分别为风电机组的切入风速、切出风速和额定风速。

1.2 直接法

根据风电场出力历史数据，基于先进的功率测量方法得到风电场出力的时间序列，此方法更加接近风电场实际的情况，故本课题以输出功率的时间序列为数学模型，采用直接法进行分析研究。

2 储能设备容量优化

文献［7］给出了风储联合发电系统的数学模型，在此基础上，按照跟踪计划控制策略计算出满足风电场及电网需求的储能设备最优容量。具体计算步骤如下。

a.利用研究周期内给出的风电场典型日出力曲线，设定风电场分段数，根据公式(2)，求出第k个时段的出力期望值，对应每个时段为水平线段。

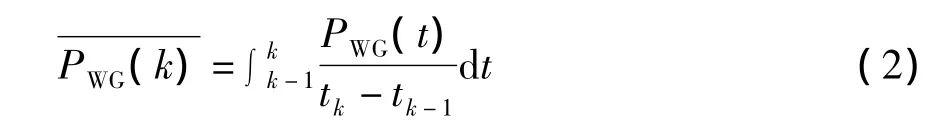
b.将研究周期内的实际输出功率PWG(t)与相应时段的比较，若大于该值则储能设备存储其差值，若小于该值则小于的部分由储能设备释放功率补充，以使其按期望值输出。

c.由公式(3)计算风电场需要配置的储能设备容量。

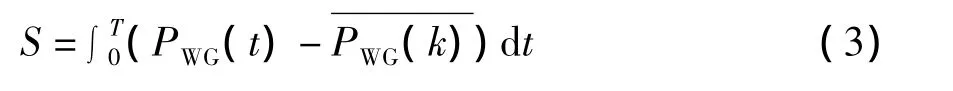
3 火电机组出力计算

在大多数研究考虑风电并网的输电规划文献中，认为系统中的火电机组出力确定;而在实际上由于风电场出力是变化的，为满足系统供需平衡，火电机组的出力也随之变化。

假定某区域电力系统配置n台机组，其发电成本与输出功率Pi关系ci由式(4)表示［8］:

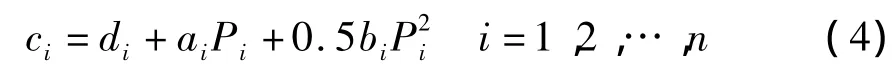
式中:ai、bi、di均为第i台发电机燃料消耗函数的系数。

以经济调度最优原则求出各机组出力Pi:

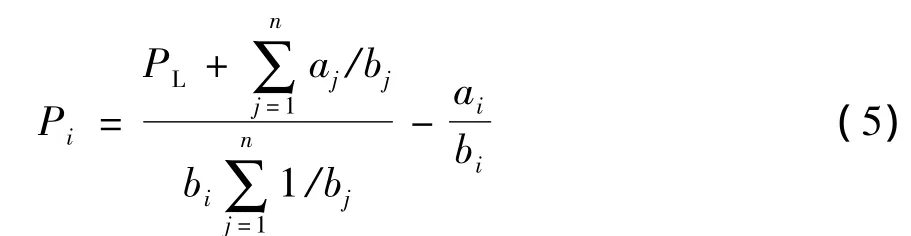
式中:aj、bj均为第j台发电机燃料消耗函数的系数。

设定风电场具有优先上网权，其输出功率系统全部能够接纳，则PL为总负荷减去风储联合系统出力。

4 风储联合系统输电规划模型

考虑研究周期内风电火电储能售电收益及发电成本，输电网架及储能设备的投资，线路的运行费用，由于风电场和火电厂是在研究周期之前就建好的，故不考虑其建设投资，以电网的年总效益最大化为目标的建立风储联合系统输电规划模型如下:

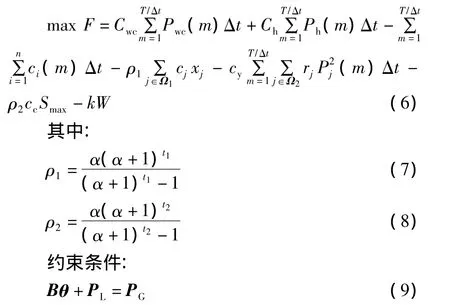
式中:F为电网年总效益;式(6)第1部分为风储联合系统售电收益;Cwc为风储联合系统上网电价;Pwc(m)为第m分段风储联合系统出力;Δt为每个分段包含时间;T为研究周期包含时间;式(6)第2部分为火电厂售电收入;Ch为火电上网电价;Ph(m)为第m分段火电厂总出力;由于风电为清洁能源，故设风电场发电成本为0;式(6)第3部分为火电厂发电成本;式(6)第4部分为输电网线路建设费用;cj为走廊j线路建设费用;xj为走廊j扩建线路数量;Ω1为待选线路集合;Ω2为电网总线路集合;式(6)第5部分为线路运行费用;cy为网损电价;rj为走廊j的电阻;Pj(m)为走廊j在第m分段流过的功率;式(6)第6部分为储能设备投资;cc为储能设备单位容量投资;Smax为储能设备容量;ρ1、ρ2分别为输电网及储能设备现值折算为等年值的折算系数;t1、t2为以水平年为目标时，线路和储能设备使用年限;α为折现率。将惩罚项引入到目标函数中以满足系统对N约束的要求。其中，惩罚项由惩罚系数k乘以过负荷量W求出，这样最优规划结果就不会选择已经过负荷的方案。Pi为线路正常工作时的传输功率;Pimax为线路上能够传输功率的最大值;Ω为过负荷线路集合;A为系统关联矩阵;B为系统的节点导纳矩阵;Bl为支路导纳对角阵;ximax为可以选择的线路数量最大值，式(9)为直流潮流约束，式(10)为正常运行时网络潮流约束，式(11)为待选线路条数限制。

5 算例分析

5.1 风电场典型日出力曲线

以某额定容量540 MW的风电场为例，典型日出力曲线如图1所示，数据是每隔5 min采集1次，一天(24 h)共采集288个点。可以看出，风电场不设储能装置时，其输出功率的波动性很大。

1分段风电场在储能设备配合下按照期望值275 MW输出，所需要的储能设备容量为1337 MW·h，储能容量相对于风电场容量的2.47倍，储能设备容量过大。风储联合系统1分段曲线如图2所示。当风电场采用2分段输出，储能设备所需容量由S=max［S1，S2］求取，为 528 MW·h，对比1分段储能容量大幅度减少。风储联合系统2分段曲线如图3所示。当风电场采用4分段输出，储能设备所需容量为344 MW·h，对比1、2分段储能容量进一步减少。风储联合系统4分段曲线如图4所示。风电场分段区间过小，其预测功率相对误差就大，因此区间段的划分不应太小，故本文一日最大分段数为8段(如图5所示)，此时储能设备所需容量为120 MW·h，储能设备容量很小，但对应的日充放电次数增多。

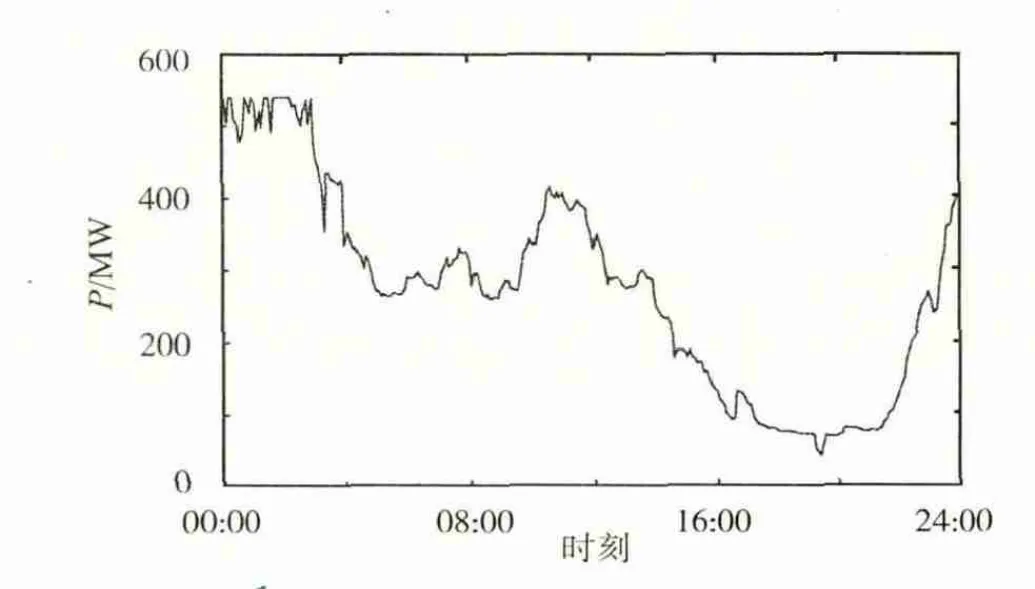
图1 风电场典型日输出功率曲线

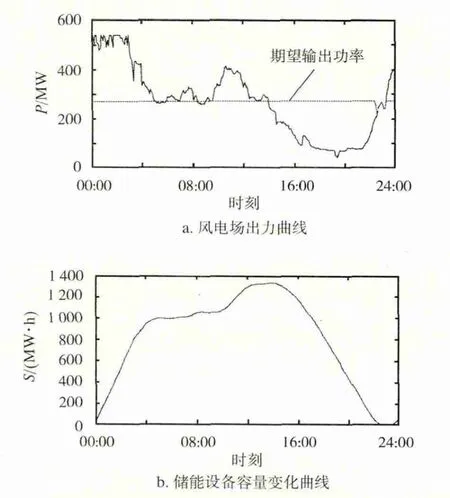
图2 风储联合系统1分段曲线

由图2到图5的a中可以看出，风电场计划出力曲线出现一个缺口，这是因为此时风况不好，而储能设备电能已经全部输出，没有多余的电能对其进行补充造成。

5.2 改进IEEE-18节点系统

在IEEE-18节点系统的14节点加入额定容量为540 MW的大型风电场。相关参数设置参照文献［9］，初始电网结构如图6所示。

图3 风储联合系统2分段曲线

图4 风储联合系统4分段曲线

5.3 参数设置

应用Matlab编制算法程序，设定人工鱼群体规模N=40，移动步长S=5，拥挤度δ=0.35，可见域V=7，最大迭代 Gmax=100次，风电上网电价为0.7元/(kW·h)，火电上网电价为0.35元/(kW·h)，18节点系统火电机组装机容量与发电成本函数的参数见表1，线路的建设成本为120万元/km，系统运行费用为0.35元/(kW·h)，运行年限为20年。储能设备平均投资价格设为600元/(kW·h)，该价格是在根据随着技术发展使得成本不断下降而得出，作为成本计算的基准［10］。储能设备充放电次数会对其寿命产生影响。将各种投资费用折算到等值年进行计算比较，折现率为0.08。

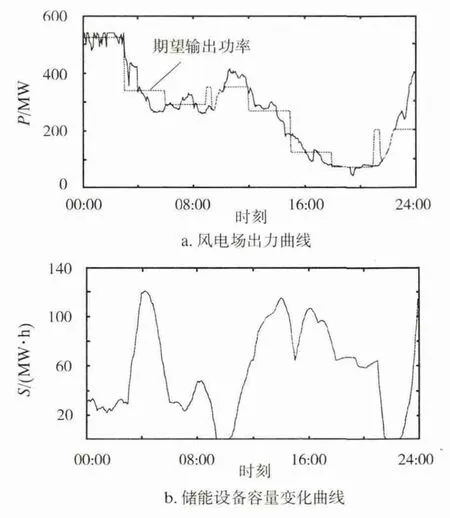
图5 风储联合系统8分段曲线

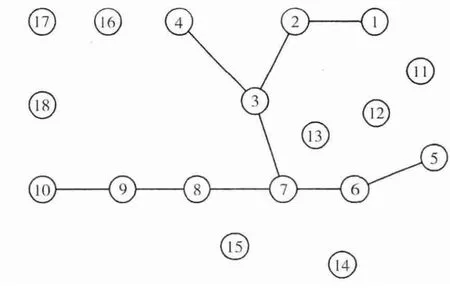
图6 IEEE-18节点系统网络结构

表1 火电机组装机容量与发电成本函数的参数

5.4 模型求解

以5.1中求出的风电场1、2、4、8分段对应的储能设备最优容量及对应的风储联合系统输出曲线为基础，利用改进人工鱼群算法求得输电网规划结果如图7至图11所示，其中实线表示已有线路，虚线表示待建线路。

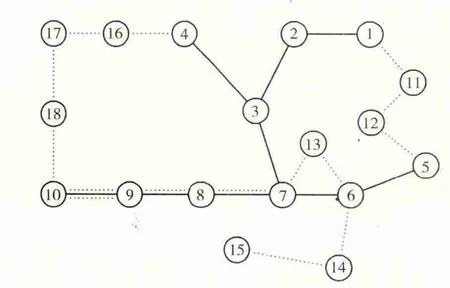
图7 风储联合系统1段输电网规划结果

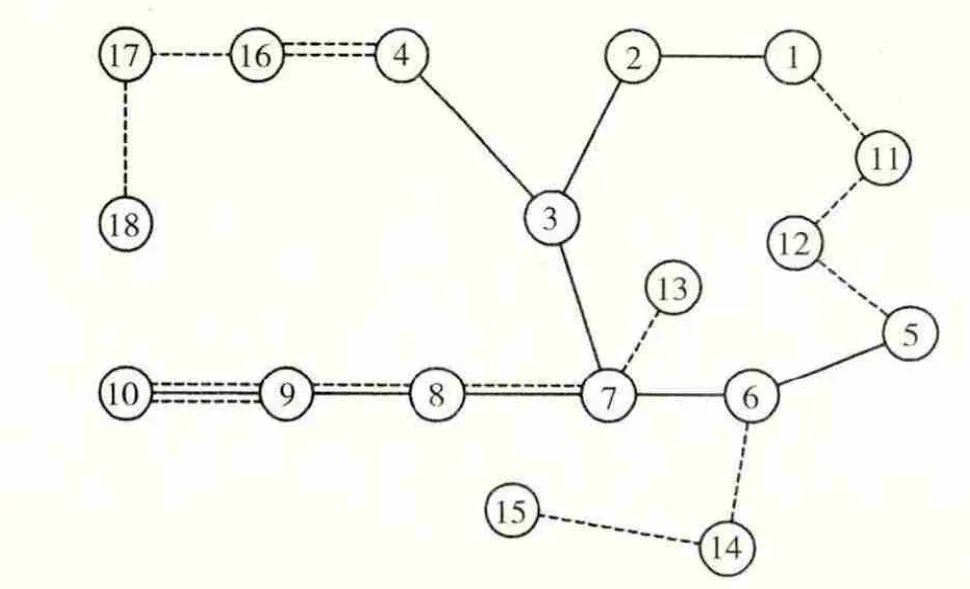
图8 风储联合系统2段输电网规划结果

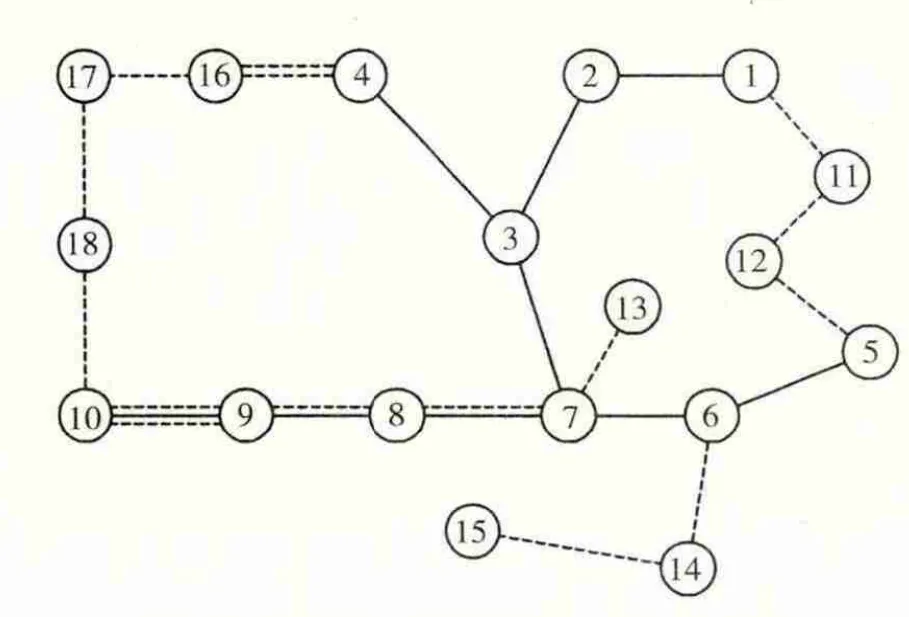
图9 风储联合系统4段输电网规划结果

图10 风储联合系统8段输电网规划结果

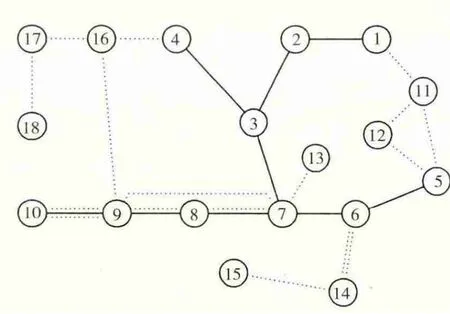
图11 无储能设备输电网规划结果

1分段所需的储能设备容量为1337 MW·h，此时输电网新建线路长达1515 km。当风电场采用2分段输出，储能设备所需容量为528 MW·h，输电网新建线路长达1615 km，较1分段长100 km。当风电场采用4分段输出，储能设备所需容量为344 MW·h，输电网新建线路长达1675 km，较2分段长60 km。当风电场分段数为8段，此时储能设备所需容量为120 MW·h，输电网新建线路长达1960 km，较4分段长285 km。当风电场中不装设储能设备时，此时风电场按照原始发电量输出，输出功率波动大，对电网产生的不利影响较大。此时输电网新建线路长达2020 km，较8分段长60 km。

为便于分析，将风电场1、2、4、8分段出力与无储能设备的电网投资进行比较，对应电网各项投资费用如表2所示。其中，风电场发电成本为0，风储联合系统售电收益与火电厂售电收益不变，分别是165470万元和923830万元。这是由于课题采用跟踪计划出力模式，且假设风电具有优先上网权，故在研究周期内风储联合系统发电总量确定，因此风储联合系统及火电厂售电收益不变。由表2可知，随着风电场分段数的增多，储能设备所需容量减小，其投资减少。然而风电场分段数增多，火电厂发电成本增大，输电网投资成本增加。比较系统总效益，当风电场4分段时，系统的总效益最大，为285330.1万元，与系统不增设储能设备相比年效益增加了1496.3 万元。对比1、2、4、8 分段及无储能对应的输电网规划结果可知，分段数越大，电网结果越复杂，建设线路长度越长。

表2 无储能与风储联合系统不同分段出力对应各项费用 万元

6 结论

本课题仅从储能容量角度出发，储能设备价格设为蓄电池的平均投资价格，没有考虑具体的储能设备选取，将复杂问题简单化。模拟得出储能设备充放电次数与寿命之间的关系，将得到更加符合实际情况的储能设备最优容量和输电网规划结果。

采用直接法，对风电场出力进行分段线性化处理，电网中其他火电机组按照最优经济调度原则配合风电场进行出力，建立考虑风储联合系统的输电网规划模型，这种方法不仅考虑了风电波动性，而且不会增加模型复杂度，同时有效节约了火电机组的发电成本，提高了电网效益。

通过对比不同分段电网效益可知，4分段出力时的输电规划方案较无储能时输电规划方案架设线路长度缩短，且此时系统总效益最大。算例验证了在风电场中投入储能设备且按一定方式运行能够有效减少输电投资，提高系统的经济性。

［1］张国伟，龚光彩，吴治.风能利用的现状及展望［J］.节能技术，2007，25(141):71-74.

［2］郭学英，郑建，梅军，等.基于超级电容储能的风电并网功率调节控制系统［J］.可再生能源，2011，29(2):28-32.

［3］卢继平，朱三立，韩涛，等.风电场储能容量合理取值范围分析［J］.重庆大学学报.2010，33(8):47-50.

［4］张浩，马爱军，李文斌，等.风电场日出力曲线和储能容量关系研究［J］.中国电力，2012，45(6):77-81.

［5］袁岳，吴博文，李振杰.基于多场景概率的含大型风电场的输电网柔性规划［J］.电力自动化设备，2009，29(10):8-11.

［6］王茜.风电场与输电网协调规划的模型和方法研究［D］.北京:华北电力大学，2011.

［7］李碧辉，申洪，汤涌，等.风光储联合发电系统储能容量对有功功率的影响及评价指标［J］.电网技术，2011，35(4).123-128.

［8］郑漳华，艾芊，徐伟华，等.基于伪并行SPEA2算法的含风电场多目标负荷调度［J］.上海交通大学学报，2009(43)，8:1222-1226.

［9］唐杰斌.考虑风能接入的多场景电网规划及其风险评估［D］.北京:北京交通大学，2011.

［10］梁亮，李建林，惠东.大型风电场用储能装置容量的优化配置［J］.高电压技术，2011，37(4):930-935.