高维数据降维中SVD与CUR分解对比分析
, , , ,
(解放军信息工程大学, 郑州 450000)
在高维空间中,由于“维数灾难”的存在,作为数据之间相似性度量的Lp距离会失去意义。高维数据包含许多冗余,其实际的维度比原始的数据维度小得多,因此高维数据可以通过降维手段转换到低维空间进行处理。高维数据的处理方法有很多种,常用的方法有SVD分解和CUR分解。SVD分解是大数据分析和处理常用的降维方法。但是,由于它线性综合了全局的信息,因此生成的数据往往过于稠密且难以解释。针对SVD分解的缺点,有人提出了CUR分解的方法[1]。CUR分解是一种从原始数据矩阵中依概率选取部分行和列构造矩阵的分解方法。CUR分解得到的矩阵由原始数据构造而来,其得到的矩阵稀疏且物理意义明确。同时,CUR分解的算法较为简单,避免了对高维矩阵进行特征值求解,因此其效率也较高。本文主要对这两种降维方法进行对比分析。
1 矩阵的SVD分解
1.1 SVD分解的一般形式
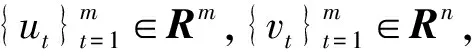
A=UΣVT
(1)
其中,Σ=diag(σ1,…,σρ);Σ∈Rm×n;ρ=min(m,n),σ1≥σ2≥…≥σp≥0,矩阵U称为A的左奇异矩阵,矩阵VT称为A的右奇异矩阵,(σ1,σ2,…,σp)称为A的奇异值。因为矩阵U和V均为正交矩阵,式(1)还可以写为UTAV=Σ。
1.2 SVD分解的存在性
下面讨论矩阵A的SVD分解的存在性[2],假设对于矩阵A∈Rm×n成立,则
(2)
当m>n时,
(3)
当m=n时,
(4)
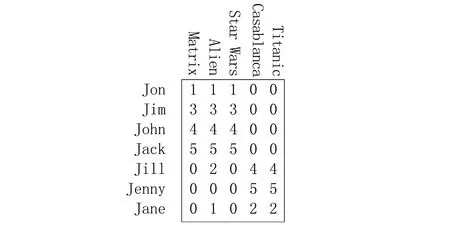
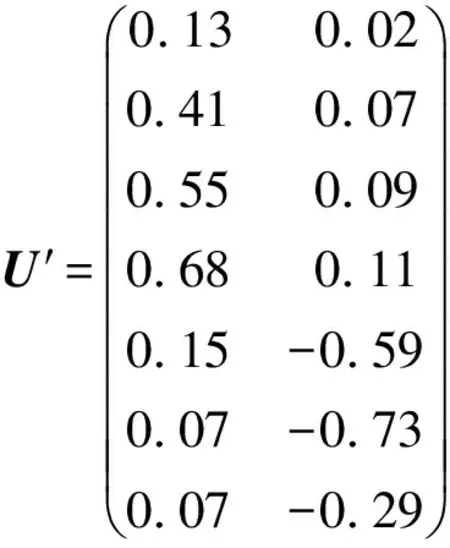
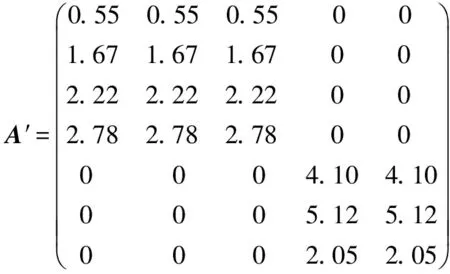
当m (5) 如果式(1)成立,由式(3)、(4)和(5)得: A=UFVT,AT=VFTUT (6) 由上式得: ATA=VΣ2VT,VT(ATA)V=Σ2 (7) 下面构造正交矩阵U、V。 (8) 构造V={v1,v2,…,vn},V∈Rn×n为正交阵,令 (9) AV=UF或UTAV=F (10) 式(10)说明矩阵A的SVD分解是存在的,且对任意的矩阵总能找到这样的分解式。 (11) 尽管SVD分解的应用非常广泛,但是从原始矩阵的列来看,特征向量ui和vi往往缺乏合理的解释。例如,个人信息矩阵经过SVD分解后,可能得到的特征向量会包括很多极小值和负值。这对于SVD分解来说是正常的,因为SVD分解是一个数学方法,可以适用于任何矩阵。而在实际应用中,有着明确物理意义的数据经过SVD分解会得到负值,这样的结果就很难给出合理的解释。 Stewart G W在线性代数领域提出了Quasi-Gram-Schmidt方法,这种方法应用到矩阵中得到了CUR分解[3-4]。Goreinov S A等提出了CUR分解(pseudoskeleton近似),并讨论了怎样选取行和列满足最大不相关理论[5-6]。Frieze A等提出依据矩阵中列的Euclidean范数的概率分布随机选择矩阵A中的列[7]。Mahoney M W等结合上述方法的优点,提出效果较好的CUR分解方法[1]。本文主要分析CUR分解过程,并与SVD分解进行对比。 CUR分解的实质是从原始矩阵中直接选取部分行和列,并以此构造3个矩阵C、U和R。给定矩阵A,为了构造矩阵C(矩阵R的构造类似),需要对A中每列计算一个重要程度值,重要程度值越大的列在构造过程中被选取的概率越大。按照这种规则进行选择,就能保证CUR是原始矩阵A的一个近似。 原始矩阵A的第j列表示为 (12) (13) 再对前k个右奇异向量计算正则化杠杆效应值: (14) (1)计算并正则化矩阵A的前k个右奇异向量的杠杆效应值; 矩阵R的构造与之类似,对AT按相同步骤处理后可得矩阵R。 定义矩阵W为矩阵C和矩阵R相交元素构成的一个k×k矩阵,对矩阵W进行如下操作: (1)计算矩阵W的SVD分解,W=XΣYT; (2)计算Σ的广义逆矩阵(Moore-Penrose pseudoinverse)Σ+; (3)令U=Y(Σ+)2XT; 这样就得到了CUR分解的3个矩阵。 对SVD与CUR分解得到的3个矩阵进行对比,可以发现其相似之处:SVD分解得到的矩阵U和V是严格正交的,这是由求解过程和特征向量性质决定的。CUR分解中构造的矩阵C和R是近似正交的,这是因为在高维矩阵中存在着“维数灾难”现象,在高维矩阵中,任意两个向量之间都是近似正交的。由于相似性,对矩阵U和V的一些处理方法在矩阵C和R上也是适用的。如果矩阵的维数较小,矩阵C和R没有近似正交,其应用会受到限制。 与SVD分解相比,CUR分解还有以下优点: (1)CUR分解非常直观,矩阵C和R都是直接从原始矩阵中按照概率直接选取的,不会产生难以解释的数据,如负值等; (2)CUR分解中矩阵C和R有着明确的物理意义,且与SVD分解的应用方法相同; (3)CUR分解的效率极高,SVD分解需要分别对矩阵ATA和AAT求特征值,在矩阵A的维数较高时计算量是非常大的。CUR分解只需要对一个低维的矩阵W进行SVD分解,其他两个矩阵计算量都比较小。 利用一个具体的实例对CUR分解及SVD分解进行比较[8]。图1是用户——电影矩阵,矩阵中列代表用户,行代表电影,矩阵中的元素表示用户对电影的评分。 图1 用户——电影矩阵 对这个电影矩阵进行SVD分解,由式(1)可以得到: (15) (16) (17) (18) 如果采用截断奇异值分解法(TSVD),保留最大的两个奇异值,可以得到如下式子: U′ΣVT′=A′ (19) (20) (21) (22) (23) 可以看到,将TSVD分解得到的矩阵相乘所得的矩阵是原始矩阵的一个近似。 利用TSVD分解的结果可以做一个简单的推荐系统,例如某用户只看过电影Matrix,对其评分为4。将该用户评分表示成向量形式: (24) 上式表明该用户可能倾向于科幻类的电影。 (qV)VT=(1.13 1.13 1.13 -0.13 -0.13) (25) 上式表明该用户可能对电影Alien和Star Wars也感兴趣。 经过SVD分解得到的矩阵包括许多负值,这在现实意义上难以解释。虽然还原后的矩阵与原始矩阵近似,但原始矩阵是非常稀疏的,而还原矩阵包含了许多极小值,非常稠密,不便处理。 对原始矩阵进行CUR分解,取k=2。 CUR=A′ (26) (27) (28) (29) (30) CUR分解得到的矩阵也是原始矩阵的一个近似。 利用CUR分解同样可以实现一个推荐系统,先对矩阵R进行正则化,然后按照与TSVD类似的方法进行处理: (qRT)R=(1.35 1.35 1.35 0 0) (31) 其结果与利用TSVD分解得到的结果是非常近似的。 再对CUR分解得到的矩阵进行观察,发现其能够克服TSVD分解的缺点。首先CUR分解中矩阵的构造来自原始矩阵,没有出现类似负值这样的异常值;其次,CUR分解得到的矩阵非常稀疏,还原后的矩阵也非常稀疏,这对于高维数据的处理是非常有利的。 SVD分解是一种传统的矩阵分解方法,生成的矩阵中包含很多极小值和负值,这在工程实际中是不好解释的。TSVD方法在SVD分解的基础之上,通过保留若干个较大的奇异值及对应的奇异向量实现降维,既在一定程度上保留了矩阵的全局信息,也去掉了大量难以解释和处理的极小值。CUR分解直接从原始矩阵中依概率选取行和列构造矩阵,物理意义明确,处理过程简单,效率较高,而实际用法与效果与SVD分解类似,优势非常明显。但是CUR依赖高维矩阵中任意两个向量正交的性质,选取行列容易受一些异常数据的干扰。 在一般情况下,SVD分解的准确性较好,CUR分解稳定性较差。在高维数据的应用场景中,对准确性并没有严格的要求,SVD分解生成的矩阵过于稠密且效率低下,而CUR分解构造的矩阵稀疏,效率较高。 参考文献: [1] Mahoney M W, Drineas P.CUR Matrix Decompositions for Improved Data Analysis[J].Proceedings of the National Academy of Sciences, 2009, 106(3): 697-702. [2] 马良荣, 张德澄.矩阵 SVD 分解法在工程数据计算中的应用[J].宁夏大学学报(自然科学版), 1998, 19(2): 125-127. [3] Stewart G W.Four Algorithms for the Efficient Computation of Truncated Pivoted QR Approximations to a Sparse Matrix[J].Numerische Mathematik, 1999, 83(2): 313-323. [4] Berry M W, Pulatova S A, Stewart G W.Algorithm 844: Computing Sparse Reduced-rank Approximations to Sparse Matrices[J].ACM Transactions on Mathematical Software (TOMS), 2005, 31(2): 252-269. [5] Goreinov S A, Tyrtyshnikov E E, Zamarashkin N L.A theory of Pseudoskeleton Approximations[J].Linear Algebra and Its Applications, 1997, 261(1): 1-21. [6] Goreinov S A, Tyrtyshnikov E E.The Maximum-volume Concept in Approximation by Low-rank Matrices[J].Contemp.Math., 2001, 280:47-51. [7] Frieze A, Kannan R, Vempala S.Fast Monte-carlo Algorithms for Finding Low-rank Approximations[J].Journal of the ACM, 2004, 51(6): 1025-1041. [8] Rajaraman A, Ullman J D.Mining of Massive Datasets[M].Cambridge: Cambridge University Press, 2012.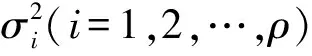



2 矩阵的CUR分解
2.1 相关研究
2.2 CUR分解的一般方法
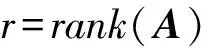
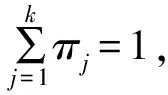

3 SVD与CUR分解对比
3.1 SVD与CUR分解异同
3.2 CUR与SVD分解实际效果比较








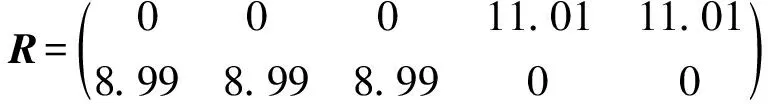
4 结 语

