直驱永磁同步风机对电力系统暂态稳定的影响研究
,
(福建工程学院,福州 350108)
现代风力发电兴起于20世纪70年代,经过多年的发展,风力发电技术已较成熟,目前风力机功率控制方式正由变桨距机组取代定桨距机组,由变速恒频取代恒速恒频,并且单机容量不断增大.高效率、高可靠性的风力发电机组正逐渐兴起,特别是无齿轮箱系统的直驱方式,可以有效地提高风力发电系统的效率和可靠性,越来越引起人们的关注.可以预计,省去齿轮箱的直驱风力发电系统将成为未来风力发电发展的主要方向.
风电场接入电力系统后对电网的影响以及电网稳定特性的变化情况,国内外科研工作者已进行了一些研究.林莉等通过在风电场进线端设定短路故障,对各个变电站的电压特性进行了分析,指出风电单元容量、故障点位置和故障持续时间是影响短路后电压稳定性的主要因素[1];张红光等分析了大容量风电场接入系统后电网的暂态稳定特性,提出了保证风电场和电网安全稳定运行的风电场安全容量概念,并且探讨了一些改善电网暂态稳定性的措施[2];迟永宁等通过研究在同一接入点分别接入双馈风电机组与同步发电组的电力系统的稳定性,证明了基于双馈风电机组的风电场对电力系统暂态稳定性的影响要好于在同一接入点接入相同容量的同步发电机组[3];曹娜等研究了恒速异步风力发电机、双馈异步风力发电机和直驱永磁同步风力发电机组成的风电场对电网的影响,比较分析了三种风电场对电网暂态稳定性的影响[4];关宏亮等提出了风电机组低电压穿越能力的概念,分析了系统中不同母线短路时对风电机组端电压的影响程度[5].
从上述文献可以看出,目前对风电场接入实际大电网的安全性、稳定性的研究往往是针对于某个方面,比如仅基于双馈发电机组,尚缺乏系统性、全面性.本文在结合已有研究成果的基础上,较全面地分析直驱风力发电机并网的稳定性问题.
1 直驱永磁同步风力发电系统
1.1 直驱永磁同步发电系统结构
直驱永磁同步发电系统结构主要包括风力机、永磁同步发电机、变流器及控制电路四大部分,其基本结构如图1所示.直驱永磁同步风机的主要特点是风力机与永磁同步发电机直接耦合,省去齿轮箱环节,既减少了噪音,又提高了可靠性.

图1 直驱永磁同步发电系统结构
1.2 直驱永磁同步发电机模型
直驱永磁同步发电机的转子为永磁式结构,转子的磁链由永磁体决定.为了更好地控制发电机,从而更好地控制发电机产生的电磁转矩和输出转速,将定子电压在dq同步旋转坐标系中进行分解,其中同步旋转坐标系的d轴方向定为转子磁链的方向.在此基础上,建立发电机定子电压的d轴和q轴分量的表达式[6]:
(1)
式中:isd和isq分别为发电机定子的d轴和q轴电流;Ra为定子电阻;ωe为电角频率,ωe=npωg;ψsd和ψsq分别为发电机定子的d轴和q轴磁链;ud和uq分别为电网电压ug的d轴和q轴分量.
定义发电机定子的d轴和q轴磁链方程:
(2)
式中:Ld和Lq分别为发电机的d轴和q轴电感;ψ0为永磁体产生的磁链.
将式(2)代入式(1)并整理,得到式(3),即在dq同步旋转坐标系中建立的直驱永磁同步发电机组数学模型:
(3)
定义q轴的反电势eq=ωeψ0,d轴的反电势ed=0.因为发电机转子为对称结构,这里假设发电机的d轴和q轴电感相等,即Ld=Lq=L,则上式可写为:
(4)
直驱永磁同步发电机的电磁转矩方程为:
Te=1.5np[(Ld-Lq)isdisq+isqψ0]
(5)
式中:np为发电机转子的极对数.
若假设Ld=Lq=L,则上式可简化为:
Te=1.5npisqψ0
(6)
根据有关理论,风力发电机组传动系统模型为:
(7)
式中:Jeq为风力机的等效转动惯量;Bm为转动粘滞系数;Te为电磁转矩;ωg为发电机转子的转速,与风力机风轮的转速ωg是相等的,即ωg=ωw.
2 电力系统暂态稳定性
2.1 电力系统暂态稳定性概念
电力系统暂态稳定性是指系统受到较大的扰动后各发电机能否继续保持同步运行的能力.由大扰动引起的电力系统暂态过程,是一个电磁暂态过程和发电机转子机械运动暂态过程交织的复杂过程.在进行稳定性分析时,通常采用如下简化方法:①忽略发电机定子绕组和电力网中电磁暂态过程的影响,只考虑交流系统中基波分量和发电机转子绕组中非周期分量的变化,这样,交流电力网中各元件的数学模型可以简单地用它们的基波等值阻抗电路来描述;②在不对称故障或非全相运行期间,忽略发电机定子回路基波负序分量电压和电流对电磁转矩的影响;③忽略发电机的附加损耗;④不考虑频率变化对系统参数的影响.
2.2 电力系统暂态稳定性分析方法
忽略发电机定子绕组和电网的电磁暂态影响,列出描述全系统暂态过程的微分方程组和代数方程组.其一般形式为:
px=f(x,y,u)
(8)
g(x,y)=0
(9)
式中:x代表状态变量;y代表网络变量;u代表输入变量.
微分方程的数值解法归纳起来可以分为显式法和隐式法,主要包括欧拉法、改进欧拉法、隐式梯度法、龙格—库塔法和亚当姆斯法等.本文采用四阶龙格—库塔法,在已知t时刻的状态变量x(t)和网络变量y(t) 的情况下,求t+Δt时刻的状态变量x(t+Δt)和网络变量y(t+Δt)(Δt表示积分步长).具体计算步骤如下:
(1)计算向量k1=Δtf(x(t),y(t));
(2)计算向量x1=x(t)+1/2k1,然后求解代数方程组g(x1,y1)=0,得到y1,最后计算向量k2=Δtf(x1,y1);
(3)计算向量x2=x(t)+1/2k2,然后求解代数方程组g(x2,y2)=0,得到y2,最后计算向量k3=Δtf(x2,y2);
(4)计算向量x3=x(t)+1/2k3,然后求解代数方程组g(x3,y3)=0,得到y3,最后计算向量k4=Δtf(x3,y3);
(5)推导出x(t+Δt)=x(1)+1/6(k1+k2+k3+k4),相应地求解代数方程组g(x(t+Δt),y(t+Δt))=0,得到y(t+Δt).
3 PSAT在电力系统稳定性仿真中的应用
仿真模型如图2所示,分析比较将母线3接入直驱风电机组与同步发电机组对电力系统暂态稳定性的影响.设置电力系统参数如下:正常风速V=15 m/s,大气密度ρ=1.225 kg/m3,电源总容量=800 MVA,负荷总容量=1 000 MVA,系统在t=1 s时断开断路器,故障持续时间为2 s,即当t=3 s时闭合断路器.
3.1 接入直驱风电机组对系统电压暂态稳定的影响
图3和图4是风机容量为75 MVA时各母线的电压波形.从图中可以看出,离故障最近的母线4的电压跌落最严重;接入风机的母线3在出现故障时出口电压跌落后在重新恢复到稳定状态的过程中所产生的波动最大;离故障点较远的几条母线的电压变化情况类似,都是在系统发生故障时电压有一定的跌落,待故障切除后,电压逐渐恢复到稳定状态.

图2 母线3接入直驱风电机组的仿真模型

图3 接入直驱风机时母线1-7的电压

图4 接入直驱风机时母线8-14的电压
3.2 不同容量的直驱风电机组对母线电压的影响
图5和图6是风机容量变化时母线3和母线4的电压波形图.从图中可以看出,直驱风机容量越大,母线电压波动越小,系统越稳定.这与电网负荷有关,如果负荷增大得多,变压器就要扩容,所以容量大时电网电压波动就小,系统就越稳定.分析表明,直驱风机容量越大,越有利于系统的稳定.

图5 直驱风机容量变化时母线3的电压

图6 直驱风机容量变化时母线4的电压
3.3 同一点接入直驱风电机组与同步发电机组分析比较
将母线3接入相同容量和电压的直驱风电机组和同步发电机组,容量为75 MVA,电压为25 kV,在其他设置都相同的情况下,对功率角和母线电压进行比较.
3.3.1 对功率角特性的影响
电力系统暂态稳定性分析主要针对系统在遭受大干扰后,同步发电机组维持同步运行的能力.发电机同步是保证电力系统正常运行的必要条件,大型风场集中并入电网对同步机功率角δ稳定性的影响是含风电电力系统暂态稳定性研究的首要问题.
图7和图8是风机接入前后各同步发电机的功率角特性曲线图.从图中可以看出,所有同步电机的功率角在系统未发生故障时是稳定的,在接入断路器时有稍许跌落,然后逐渐增大;同步电机未接入风机时功率角呈抛物线式上升,最后趋于稳定,而接入风机时功率角增大到一个峰值后又减小,然后放慢趋于稳定,波动幅度较大;同步电机接入风机后,同步电机的功率角较未接入风机有所增大.分析表明,接入风机对系统功率角的稳定性较为不利.

图7 未接入直驱风机的功率角特性曲线图
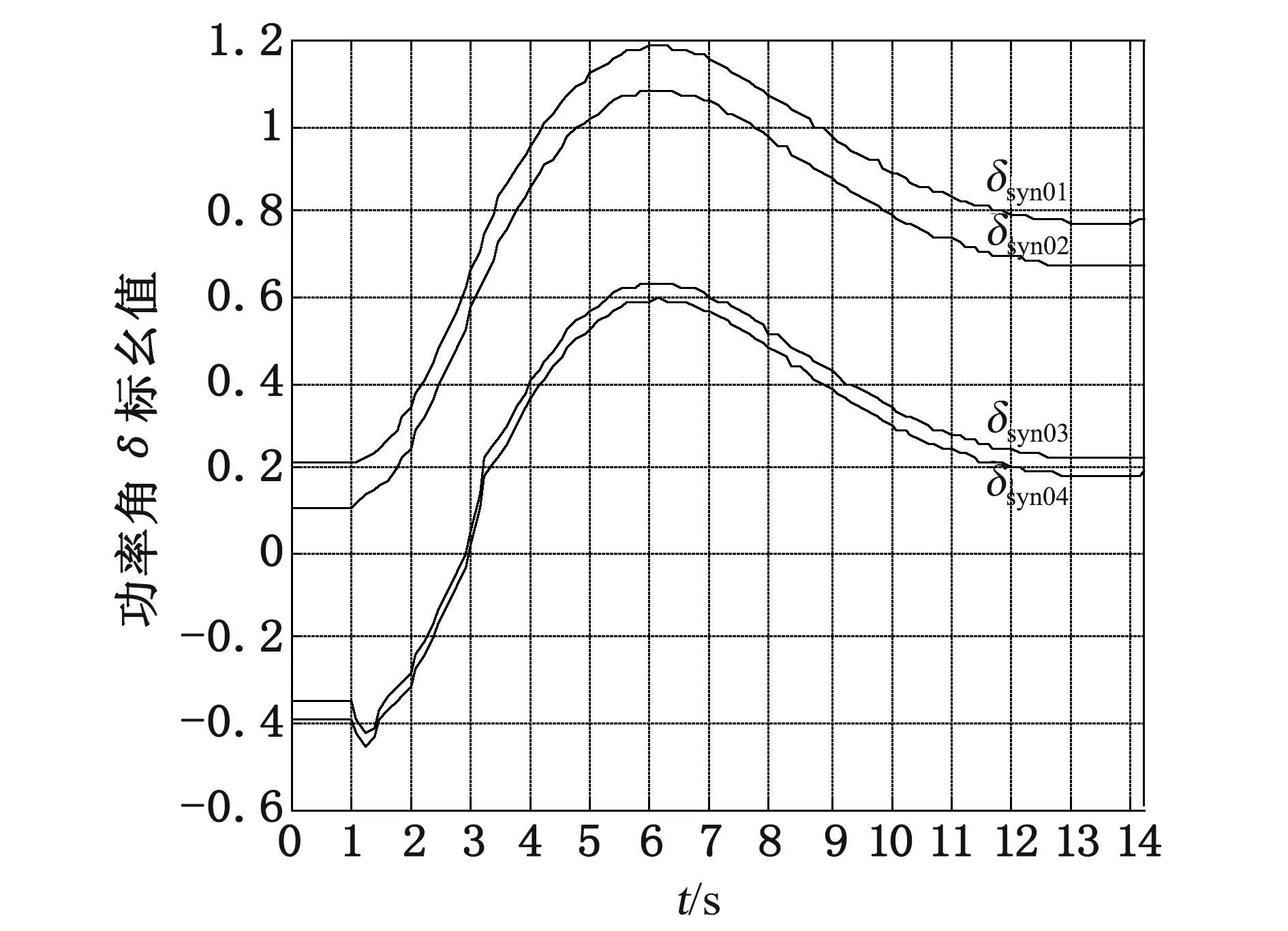
图8 接入直驱风机的功率角特性曲线图
3.3.2 对母线电压的影响
图9—图12是母线2、3、4、13在接入风机与未接入风机时的电压暂态变化比较图.母线2的电压在故障期间波动幅度很大;母线3在接入风机后,风机出口电压在系统发生故障时跌落严重,故障切除后,经过较长时间的较大振荡逐渐趋于稳定;母线4和母线13接入风机后,电压在系统发生故障时跌落比未接入风机时厉害,波动较为严重,趋于稳定所需时间更长.分析表明,所有的母线电压均在系统接入风机后稳定性变差,但是母线离故障点越远受影响越小.

图9 母线2的电压变化曲线图

图10 母线3的电压变化曲线图

图11 母线4的电压变化曲线图

图12 母线13的电压变化曲线图
4 结 语
本文对直驱同步风电机组各部分功能进行了分析,根据直驱同步风电机组dq坐标系中的数学模型,利用仿真软件PSAT搭建了仿真模型.仿真结果表明:
(1)电力系统接入采用直驱风电机组的风电场后,其暂态稳定性受到一定的影响,当电力系统发生扰动时,离故障点近的电压的稳定性比离故障点远的电压的稳定性差.
(2)在相同的计算条件下,将不同容量的风电场接入电网,对电力系统的暂态稳定性有不同的影响.在本文给定情况下,随着风力发电机容量的增大,电网的暂态稳定性有所增强.
(3)当外部条件相同,电网中某点发生短路故障时,相同容量的直驱风电机组和同步发电机组对同步发电机稳定极限的影响不同.从能量平衡角度来看,在系统故障期间由于电磁转矩和机械转矩不平衡,会导致直驱风电机组加速,其中一部分能量会暂存在风电机组叶片与转子加速旋转的动能中,系统的各参量变化得更明显,波动幅度更大.因此,接入采用直驱风电机组的风电场的电力系统的暂态稳定性要差于在同一点接入相同容量同步发电机组的电力系统的暂态稳定性.
参考文献:
[1] 林莉,孙才新,王永平,等.大容量风电场接入后电网电压稳定性的计算分析与控制策略[J].电网计术,2008,32(3):41-46.
[2] 张红光,张粒子,陈树勇,等. 大容量风电场接入后电网的暂态稳定特性和调度对策研究[J].中国电机工程学报,2007,27(31):45-51.
[3] 迟永宁,王伟胜,刘燕华,等. 大型风电场对电力系统暂态稳定性的影响[J].电力系统自动化,2006(15):10-14.
[4] 曹娜,李岩春,赵海翔,等.不同风电机组对电网暂态稳定性的影响[J].电网技术,2007,31(9):53-57.
[5] 关宏亮,赵海翔,戴慧珠.风电机组低电压穿越功能及其应用[J].电工技术学报,2007,22(10):173-177.
[6] 尹明,李庚银,张建成,等.直驱式永磁同步风力发电机组建模及其控制策略[J].电网技术,2007, 31(15):61-65.

