基于统计模糊权重和模糊区间评价的采矿方法优选模型
姚 囝,叶义成,王其虎,施耀斌,鲁 方(武汉科技大学资源与环境工程学院,湖北 武汉 )
在地下矿山企业中,采矿方法的选择是否合理决定了整个矿山的生产运营效果及各项技术经济指标的优劣。采矿方法的优劣受多项技术经济指标影响,且各影响因素直接的关系也不明确,构成一复杂的应用系统问题。因此,在传统的采矿方法选择中,经验类比法和盈利分析法存在较大的片面性和主观性[1]。
随着系统工程以及计算机技术的发展,人们将系统工程方法应用于采矿方法优选,显现出明显的优势。目前,采矿方法优选决策方法主要有层次分析法、模糊数学评价法、灰色关联分析法、多目标决策法、集对分析法、神经网络法[2]、突变理论[3]等。这些数值优选方法应用难点一是采矿方法评价指标及其权重值的确定往往根据专家的经验判断,主观随意性较强[4];二是采矿过程中有很多的不确定性[5],影响因素中既有定性指标也有定量指标,如安全性、工艺复杂程度等属于定性指标,生产能力、损失率等属于定量指标,定性指标评价值难以准确量化,定量指标也往往是一个区间范围。这些问题直接影响采矿方法优选的可靠性和优选决策方法的应用推广。
统计计算方法是在难于精确解析计算系统结果条件下广泛使用的技术之一,通过对大量采矿行业专家在采矿方法优选过程中评价指标及其权重值的统计分析,能较好地减少主观性,使权重值更加合理。同时,模糊区间变量是量化专家语言评价的有效方法,模糊区间评价能较好的表达决策者对各方案中的评价态度,并能将复杂系统中的模糊判断和模糊决策定量化。因此,研究基于统计方法的指标权重值计算方法和模糊区间评价方法,探讨采矿方法优选应用,可增加计算结果的客观性,丰富采矿方法优选理论。
1 统计模型指标权重值确定
1.1 常用赋权法
目前,常用的指标权重确定方法主要有三种:一是主观赋权法,即根据专家的经验判断得到指标权重,具有较强的主观随意性,如相对比较法、连环比率法、专家咨询法、层次分析法(AHP)等,其中AHP能将定性问题定量化,操作简单方便,是目前应用最广的主观赋权法;二是客观赋权法,即通过分析计算评价指标的评价数据值的内在关系来确定指标权重,具有较强的数学理论依据,一般能在较大程度上区分评价方案的优劣,但只注重本身的信息,容易与指标的实际重要程度不符,如熵值法、拉开档次法、逼近理想点法等,其中应用较多的是熵值法[6];三是组合赋权法,即采用主观赋权法与客观赋权法进行组合赋权[7],一般是先分别进行主、客观赋权,在根据具体情况确定主、客观赋权法权重系数所占的比例,最后求出综合评价权重值。组合赋权法虽然在某种程度上能兼顾前两种赋权法的优点,但不可避免的会同时具有两种赋权法的缺点,因此并不一定能达到完好解决问题的目的。
有鉴于此,很多学者对采矿方法数值优选的评价指标权重值确定进行了研究。陈建宏[8]等提出用区间数来表征指标权重值,用区间数来代替确定数表示指标权重值,谢胜军等[9]提出用模糊数来表征指标权重值,均能较好地描述采矿指标的不确定性;杨仁华[10]等提出基于变权法的指标权重赋权法,在评价过程中权重值随评估向量变化,能增大评价值较低的指标权重值,突出单因素评估中评估值较低的项。
1.2 基于统计方法的指标权重值确定
1.2.1 评价指标选取
为合理确定采矿方法数值优选评价指标及其权重值,统计分析了100篇地下矿山采矿方法优选方法模型的学术论文,将近期论文和被引次数多的论文在统计中视作同等重要,选用近期发表论文57篇(2007年至今),按被引次数排名靠前论文57篇,其中14篇既为近期发表又为被引次数较多论文。统计论文中采矿方法选择评价指标及其权重值,选择被选为评价指标次数大于10次的评价指标,共14个,见图1。由图1可见,被选次数最多的评价指标是损失率(92次),大于60次的有7个,定义为重要评价指标,10~60次的有7个,定义为一般评价指标,与采用ABC分类法划分的结果基本相同。
1.2.2 指标权重计算
经统计表明,采用AHP计算指标权重值的论文接近半数(48篇),专家打分法9篇,熵值法2篇,组合赋权法3篇,变权法2篇,另外有部分未计算指标权重值的论文。由统计可见,主观赋权法是常用的指标权重值计算方法,而AHP是应用最多的主观赋权法。在未计算指标权重值的论文中,部分是采用工程类比法等方法进行采矿方法选择,不需要计算权重值,部分是作者在数值优选过程中未对指标权重进行处理,可解释为作者认为所选的评价指标具有同等重要性。因此,对于此类数据,在统计指标权重时,各评价指标权重值为选择的评价指标个数的倒数。
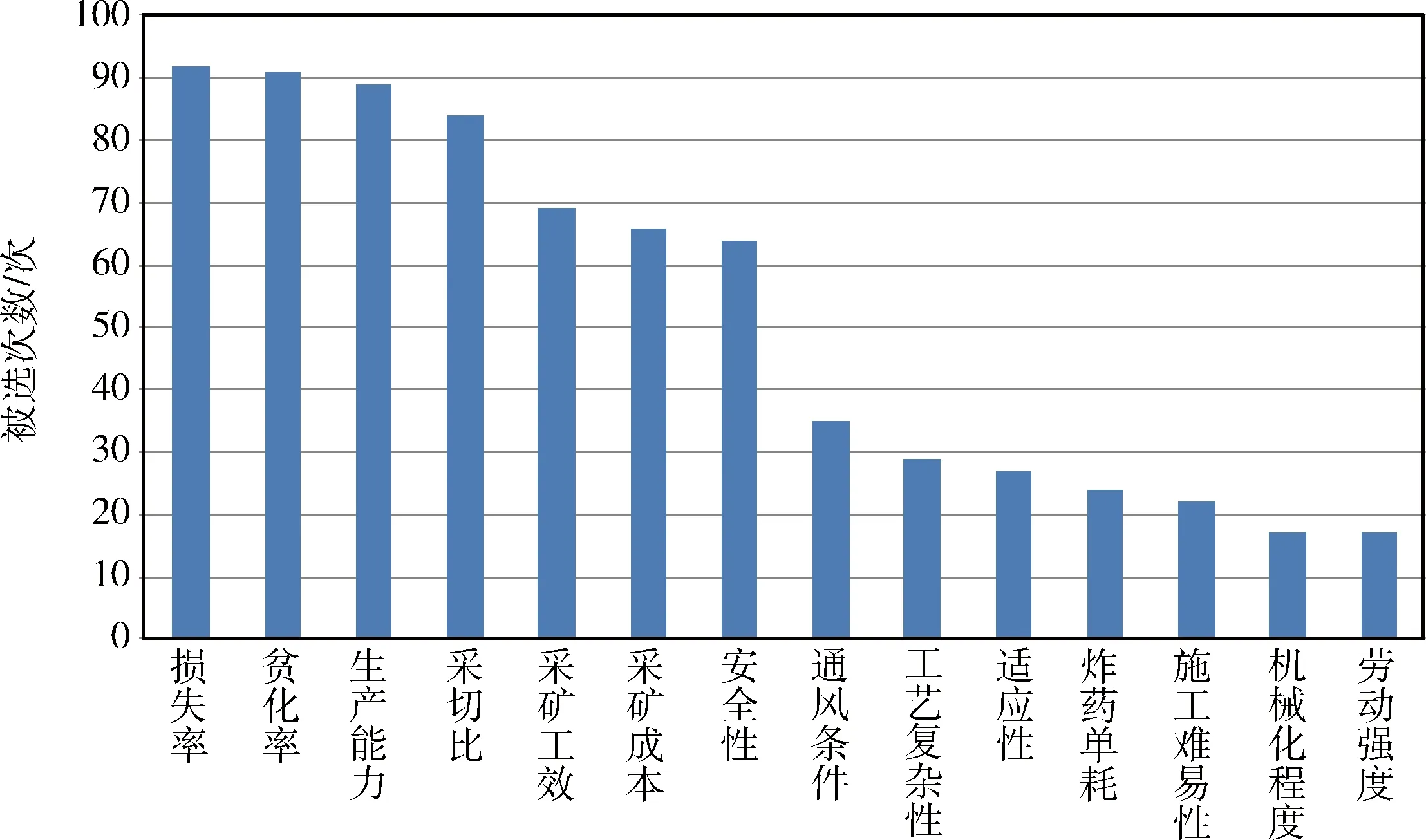
图1 评价指标被选次数(注:本次统计文章主要来源于采矿与安全工程学报、中南大学学报(自然科学版)、广西大学学报(自然科学版)、北京科技大学学报(自然科学版)、西安建筑科技大学学报(自然科学版)、金属矿山、矿冶工程、黄金、有色金属、矿业研究与开发、化工矿物与加工、价值工程、集成技术等期刊,由于统计的论文数量较多,无法在参考文献中一一列出。)
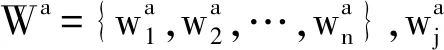
(1)
(2)
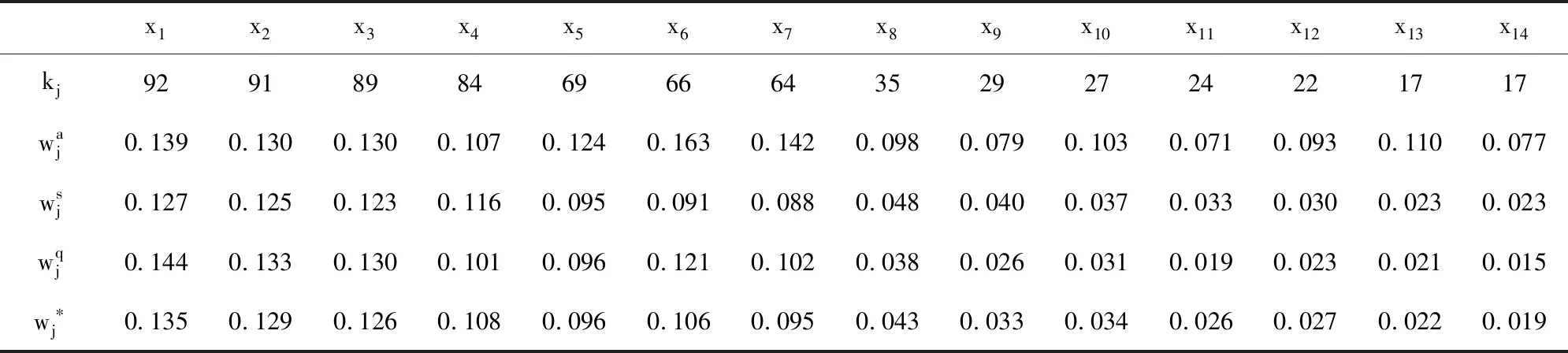
(3)
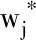
定义模糊区间数D,当D=(d1,d2,d3)时,则d1、d2、d3分别表示D的最小值、最大可能值、最大值。因此,定义指标模糊区间权重值wj,见式(4)。
(4)
表1中计算了14个评价指标的权重值,对于一般的采矿方法选择来说,对应的数值优选过程中的数学计算量比较大,因此,为了计算简便,可以仅考虑重要评价指标,即被选次数大于60次的指标。仅考虑重要评价指标的权重值计算方法同上,计算结果见表2。
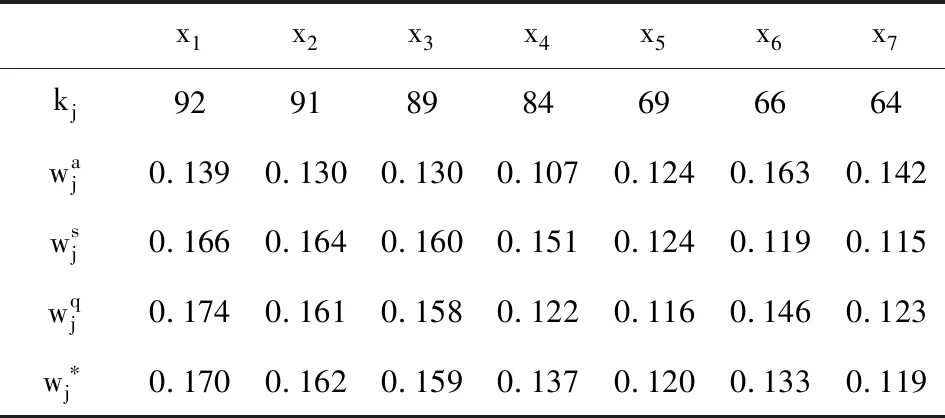
表2 仅考虑重要评价指标的权重值计算
2 模糊区间评价
2.1 评价模型建立
设m个方案A={A1,A2,…,Am},n个评价指标X={x1,x2,…,xn},xij=(aij,bij,cij),xij表示对第i个方案针对第j项评价指标的区间评价值,aij、bij和cij分别表示xij的最小值、最大可能值、最大值。
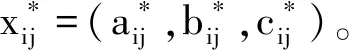

(5)
设xij和wj用模糊区间数表示分别为:xij=(aij,bij,cij),wj=(ej,fj,gj),方案Ai的模糊区间评价值Si见式(6)。
⊗[(xi1⊗w1)⊕…⊕(xin⊗wn)]
(i=1,2,…,m)
(6)
为简化计算过程,定义式(7)。
Si=(Pi,Qi,Ri) (i=1,2,…,m)
(7)
式(7)中的各个函数表示见式(8)。
(8)
2.2 区间评价步骤
1)最大可能值排序[11]。根据式(8)中计算出的最大可能值Qi对方案进行排序,Qi越大,方案越优。
2)区间数排序[8]。取Hi=(Pi,Ri),按一定计算规则计算区间优度,并对各区间数进行排序。
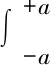
区间数a和b可能的区间数关系有相离、相交和包含三种,可能的概率分布见图2。
定义a优于b的可能度p(a≥b)见式(9)。
(9)
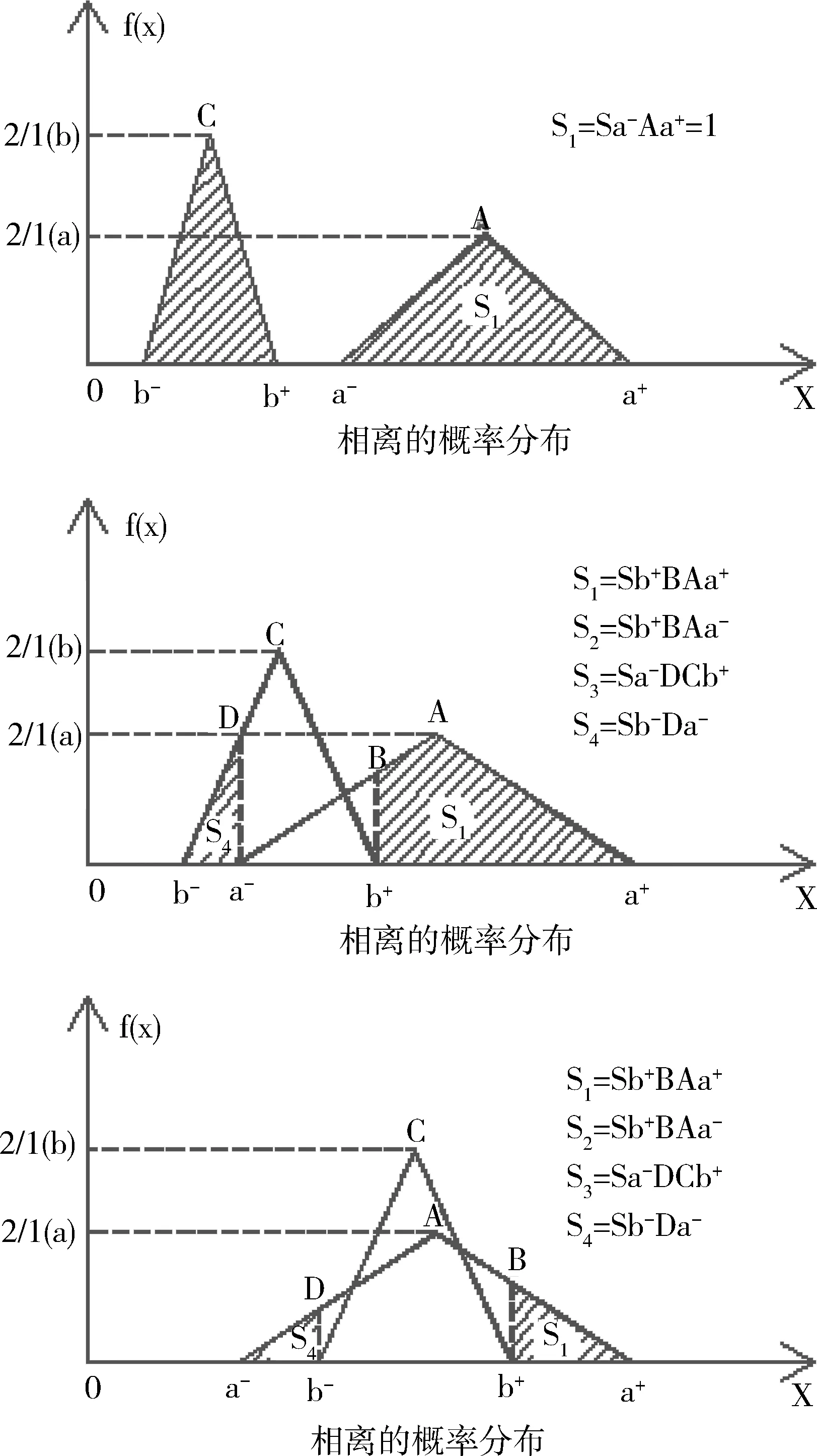
图2 两区间数可能的概率分布关系
根据两区间数的相对位置不同,会产生六种情况。区间优度p值越接近1,则a越优于b。如式(9)的第二种状态,由图2中相交的概率分布可见,S1、S2、S3、S4分别表示区间数a取值在区间(b+,a+)、(a-,b+)及区间数b取值在区间(a-,b+)、(b-,a-)的概率。当a取值在区间(b+,a+)时,无论b取何值,a>b,此概率为S1;当a取值在区间(a-,b+)且b取值在区间(b-,a-)时,a>b,此概率为S2·S4;当a和b取值均在区间(a-,b+)时,有一半的可能性a>b,此概率为S2·S3/2。综合以上三种情况,该分布特点下a优于b的可能度p=S1+S2·S4+S2·S3/2。
3)最终排序。将以上两种排序值进行综合考虑,得到最终排序值Ui。由式(9)计算出的区间优度p构成区间优度矩阵,计算矩阵的最大特征值对应的特征向量R=(r1,r2,…,rm),最终排序值Ui可由式(10)计算,Ui越大,方案越优。
Ui=w1·Qi+w2·ri
(i=1,2,…,m;w1+w2=1)
(10)
最大可能值排序为绝对排序,即所有方案进行全排序。区间数排序为相对排序,即两两方案进行比较排序,然后组合在一起形成全排序。由于区间的上下界为可能的最大值和最小值,采用区间评价时,能较好地考虑风险的因素。由图2可见,该概率密度函数认为,最大概率密度为区间数中点,且向区间两端概率呈一次线性函数减小,符合概率统计学的原理,具有较好的现实意义。同时,该方法简单可行,能简便地计算出两区间数的区间优度评价数值。
3 应用实例
某矿床呈多层层状、似层状平行产出,矿体倾角5~25°,矿体长度一般为224~670m,倾斜延深87~204m,矿石层厚度一般为0.81~5.54m,夹石层厚度5~12m。矿岩稳固性较好,矿区工程地质条件属简单-中等类型。根据环保及相关政策要求,地表不允许塌陷。
根据该矿的开采技术条件,初步选择全面采矿嗣后充填法(A1)、浅孔房柱嗣后充填法(A2)、壁式充填法(A3)和分段矿房嗣后充填法(A4)等4种采矿方法作为备选方案。确定评价指标为表2内的7个重要指标:损失率(x1)、贫化率(x2)、生产能力(x3)、采切比(x4)、采矿工效(x5)、采矿成本(x6)和安全性(x7)。对表2的数据采用式(4)可求出评价指标的模糊区间权重值wj,见表4。

表4 评价指标的模糊区间权重值
参考国内外采用这4种采矿方法的类似开采条件的矿山实例,给出4种采矿方法针对各定量指标的推荐范围,取范围内平均值作为最大可能值,构成指标的区间评价值。对于定性指标,则采用主观评价,由于采矿成本受诸多因素影响,变化较大,数据统计困难且意义不太大,因此,采矿成本(x6)和安全性(x7)一起作为定性评价指标,其余指标作为定量评价指标。相应区间评价原始数值见表5。经过式(5)标准化后的模糊区间评价值见表6。
1)最大可能值排序。根据式(8)计算有Qi=(0.0664,0.0775,0.0852,0.1022),各方案按最大可能值排序为A4≻A3≻A2≻A1,即四种方案按最大可能值排序的优劣顺序为:分段矿房嗣后充填法A4,壁式充填法A3,浅孔房柱嗣后充填法A2,全面采矿嗣后充填法A1。
2)区间数排序。根据式(8)分别计算出Pi和Ri,再根据式(9)计算区间优度p,计算出的区间数及其区间优度矩阵见表7。由表7可见,方案A4优于A1、A2、A3的区间优度分别为1.0000、0.9745、0.7494,因此A4为最优方案。根据方案两两比较的结果,被选方案区间数排序为A4≻A3≻A2≻A1,与最大可能值排序相同。

表5 方案区间评价原始数值
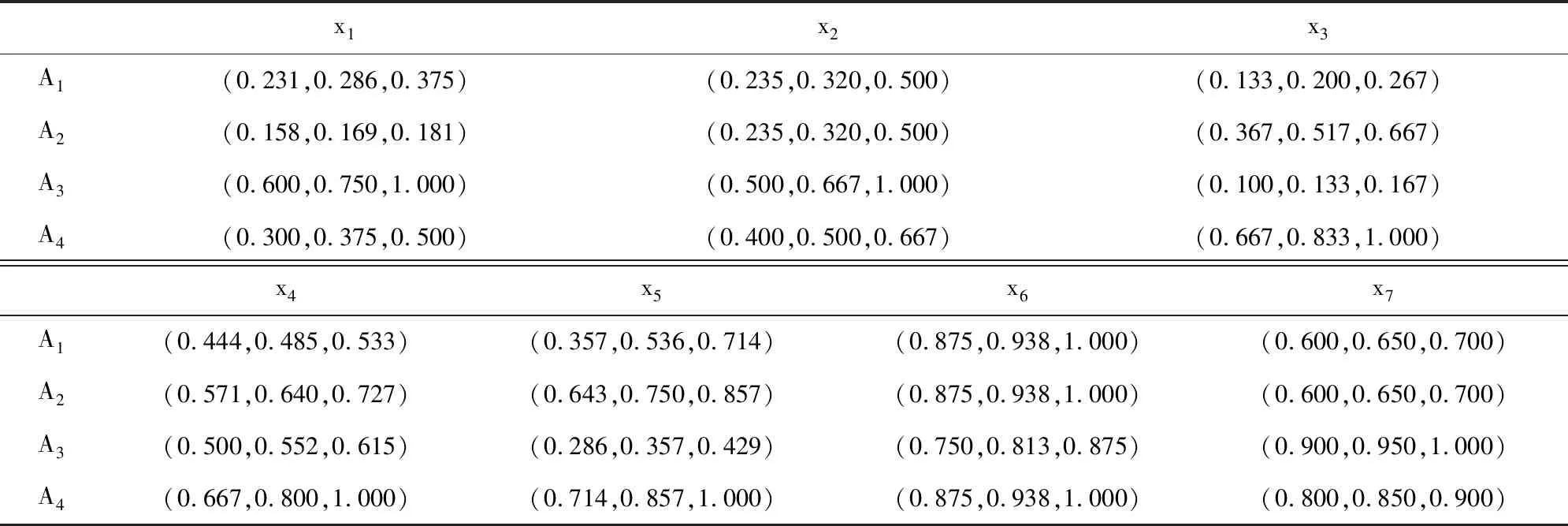
表6 标准化后的方案模糊区间评价值
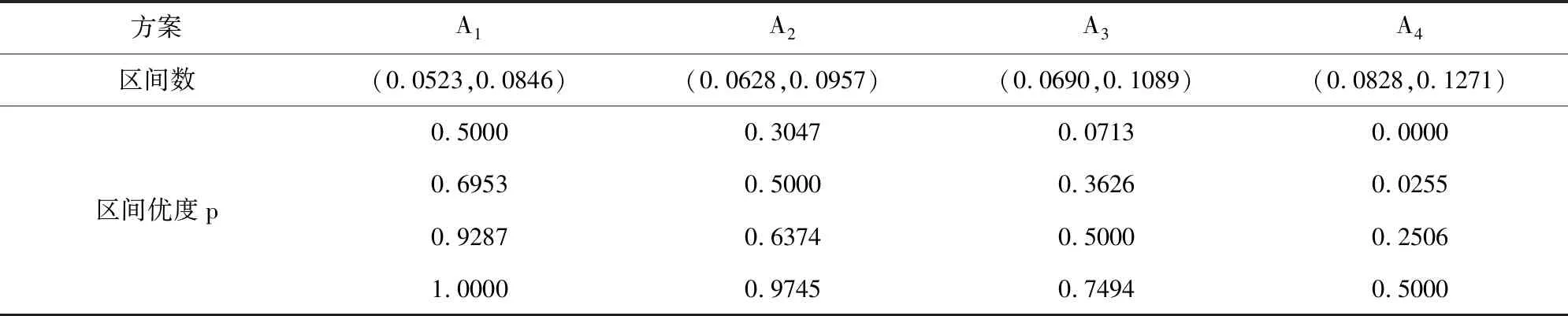
表7 区间数及其区间优度
3)最终排序。根据表7中的区间优度矩阵,计算其最大特征值对应的特征向量为R=(0.0108,0.1456,0.3192,0.4754),根据式(10)计算有Ui=(0.0386,0.1115,0.2022,0.2888),式(10)中取w1=w2=0.5,即认为两种排序同等重要。由于本例中按以上两种排序方式的方案排序结果完全相同,因此最终排序也会是相同的排序结果,即最优方案为分段矿房嗣后充填法A4,随后依次为壁式充填法A3,浅孔房柱嗣后充填法A2和全面采矿嗣后充填法A1。
4 结语
1)基于统计方法计算的指标模糊区间权重值,综合分析了大量采矿行业专家在采矿方法优选过程中评价指标模型,将评价指标被选次数统计的指标权重值、带权重统计的指标权重值以及二者综合考虑的指标权重值构成的指标模糊区间权重值,既考虑了综合评价的专家判断,同时也避免了应用中采矿方法选择时决策人员的主观片面性,更符合决策过程中的模糊性和不确定性,使权重值更加合理。
2)运用模糊区间评价结合模糊区间权重值确定方法对采矿方案进行综合评价,避免了主观分配指标权重值的主观性,采用最大可能值排序与区间数排序的相结合的排序方法,指标权重值和指标评价值均采用模糊区间数表示,既能较好地模拟评价过程中的模糊不确定性,同时能较好地考虑风险的因素。
3)定义推导了一种区间优度函数,提出了新的区间数排序方法,并详细说明了它的概率统计意义。该方法简单可行,能简便地计算出两区间数的区间优度评价数值,对区间数优度评价具有较强的可操作性。
4)研究了基于统计模糊权重和模糊区间评价的采矿方法优选模型的矿山采矿方法优选实例,方案A4优于A1、A2、A3的区间优度分别为1.0000、0.9745、0.7494,与计算最可能大值排序(0.0664,0.0775,0.0852,0.1022)得出的方案排序一致,最终排序为(0.0386,0.1115,0.2022,0.2888),因此选择了分段矿房嗣后充填法A4作为最终方案,同时验证了区间数排序的正确性。该方法对于采矿方法优选具有一定的参考价值。
[1] 龚声武,蔡明悦,李夕兵.AHP-FCE法在采矿方法优选中的应用[J].采矿与安全工程学报,2009(1):41-44,49.
[2] 吴爱祥,郭立,余健,等.采矿方法模糊优选的神经网络模型构造及其应用[J].矿冶工程,2003(3):6-8,11.
[3] 白云飞,叶振华.基于突变优选理论的采矿方法选择[J].金属矿山,2011(10): 61-63,67.
[4] 刘方.金属矿山地下采矿方法选择系统[D].武汉:武汉理工大学,2010.
[5] 王新民,赵彬,张钦礼.基于层次分析和模糊数学的采矿方法选择[J].中南大学学报:自然科学版,2008(5):875-880.
[6] 王新民,刘贱刚,张钦礼.基于信息熵层次集评价方法的采矿方案选择[J].化工矿物与加工,2011(7):18-21,25.
[7] 邓红卫,胡普仑,杨念哥,等.基于组合赋权TOPSIS的采矿方法优选[J].广西大学学报:自然科学版,2012(5):990-996.
[8] 陈建宏,刘浪,杨珊,等.灰色理论与区间数多属性决策在采矿方案优选中的应用[J].西安建筑科技大学学报:自然科学版,2010(6): 899-906.
[9] 谢胜军,蔡嗣经,李有臣.基于模糊多属性决策的南芬铁矿露天转地下采矿方法优选[J].集成技术,2013(3):98-104.
[10] 杨仁华,陈玉明,罗红萍.基于变权法的采矿方法模糊综合评判选优[J].金属矿山,2010(11):47-50.
[11] 叶义成,柯丽华,黄德育.系统综合评价技术及其应用[M].北京:冶金工业出版社,2006.
——拟合优度检验与SAS实现

