基于低偏差序列的矿井供水管网可靠性

蒋仲安，王佩，施蕾蕾，谭聪

(北京科技大学 金属矿山高效开采与安全教育部重点实验室，北京，100083)

矿井供水管网作为矿山安全避险六大系统之一，其可靠稳定运行是保证综合防尘效果的重要基础。一个完善可靠的防尘供水系统能够维持矿山正常的采掘工作，保证矿工具有安全的工作环境，同时供水管网是防治井下粉尘危害的重要设施，因此对矿井防尘供水管网的可靠性进行研究非常必要。国内对城市供水管网可靠性研究较多，方法也众多。而矿井供水管网研究较少[1-3]，主要分析方法有故障树分析法[4]和GO 法[5-6]。针对传统蒙特卡罗法[7-9]收敛速度较慢以及计算结果不够稳定的问题[10]，本文作者采用拟蒙特卡罗法对矿井供水管网水力可靠性进行研究。该方法采用Sobol 序列进行抽样替换了传统蒙特卡罗法的伪随机数，加快了收敛速度，提高了仿真结果的稳定性。在对管网进行分析的过程中，将综合考虑机械故障和水力条件变化对管网可靠性的影响，并运用EPANETH 管网平差软件进行水力模拟，以模拟结果为基础值代入水力可靠性分析模型进行计算。EPANET 管网平差软件是美国环保局开发的一款免费软件，它可以通过自带组件绘制管网模型，还包含强大的水质、水力模拟能力，而EPANETH 是其汉化版。

1 拟蒙特卡罗法

拟蒙特卡罗法(OMC)是基于蒙特卡罗法的一种改进方法，采用在采样空间分布更加均匀的拟随机数代替传统蒙特卡罗法中的伪随机数。拟随机数一般由低偏差序列通过某种变换得到。拟蒙特卡罗法计算的收敛速度和结果的准确性主要取决于偏差。偏差用来度量点列在函数域上分布的均匀程度，偏差越小，点列分布越均匀，收敛速度就变快，波动也随之减小，计算准确度就相应地提高[11]。

根据Kokama-Hlawka 定理[12]，低偏差序列M 用于蒙特卡罗积分时具有确定的误差上界。因此拟蒙特卡罗法的计算误差可由Kokama-Hlawka 不等式给出：

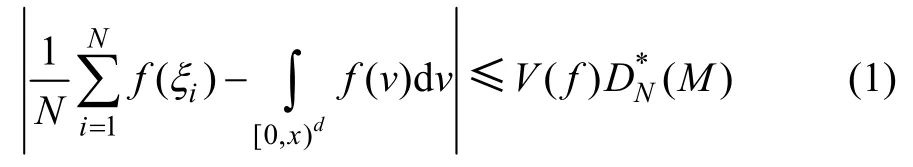
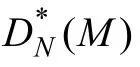
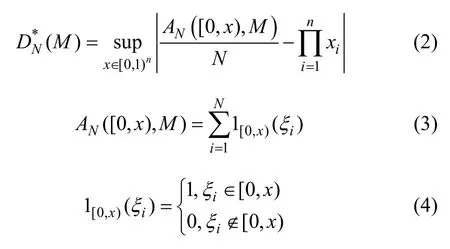
式中：AN([0,x),M)为序列M 中的N 个样本在区间[0,x)中的数量。

由于Sobol 序列较其他序列收敛效果好，计算精确，本文首次采用Sobol 序列用于矿井防尘供水管网的可靠性计算。Sobol 序列的产生方法如下[15]：

Sobol序列是基于一组叫做“直接数”的数vi而构造的。设mi是小于2i的正奇数，则vi=mi/2i。

vi的生成借助于系数只为0 或1 的本原多项式，多项式可表示为

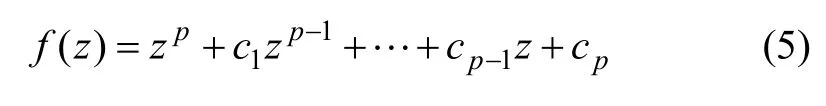
对于i＞p，存在递归公式：

式中：⊕为二进制按位异或运算符。

对于任何一个十进制整数n，可以唯一表示成与数基b=2 有关的式子

式中：k 为大于等于log2n 的最小整数，aj取0 或1。

则Sobol 序列的第n 个元素为：

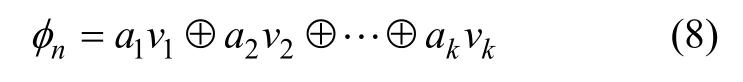
为了加快序列的产生速度，Antonov 和Saleev[16]提出了Gray code 法，可将式(17)修正为：

式中：i 为满足aj=0 的最小的j。

2 矿井供水管网水力可靠性计算

2.1 供水管网水力可靠性评价模型建立

在分析矿井防尘供水管网水力可靠性时，由于要建立数学模型，因此必须对一些参数进行界定。首先，界定管网组件只有正常与故障2 种状态，而供水节点有正常、失效以及非正常3 种状态，并且在所有管网组件中，只考虑管段故障对供水管网可靠性的影响；其次，管网组件的故障率λ 和修复时间T 均为常数，且组件或系统的故障和修复相互独立。

在分析整个管网可靠度之前，从管网中各节点着手。节点流量与水头之间的关系可用下式表示[17]：

式中：Hi为节点i 的水压；Himin为节点i 要求的最小水压；Qi为节点i 的流量；Ki为节点i 的阻力系数；ni为节点i 的阻力指数。

节点需水量和节点所需水压的关系可表示为：

式中： Qireq为节点i 的需水量；Hireq为节点i 所需水压。

由式(10)和(11)可得：

从式(10)可看出：节点流量与节点水压之间满足指数关系，因此在挑选评价指标时可只选1 个指标，本文选择节点水量作为评价指标之一。节点可用水量可用下式表示：

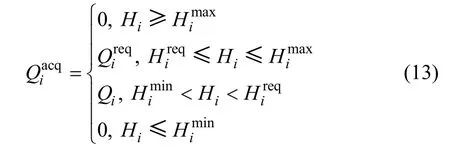
式中，Himax为节点i 能够承受的最大水压。

从式(13)可以看出：当节点水压高于所需水压且低于允许的最大水压时，水量满足要求；当水压低于所需水压、高于要求的最小水压时，水量部分满足要求；当水压高于管网能够承受的最大水压时，虽然能够提供充足的水量，但存在隐患，容易导致爆管等事故，此时定义节点失效；当水压低于要求的最小水压时，节点失效。

本文节点可靠度用需水量的满足程度表示，则节点可靠度可表示为：

式中， Rij为管网中第j 根管段发生故障时，节点i 的可靠度。

由式(13)和(14)可得：

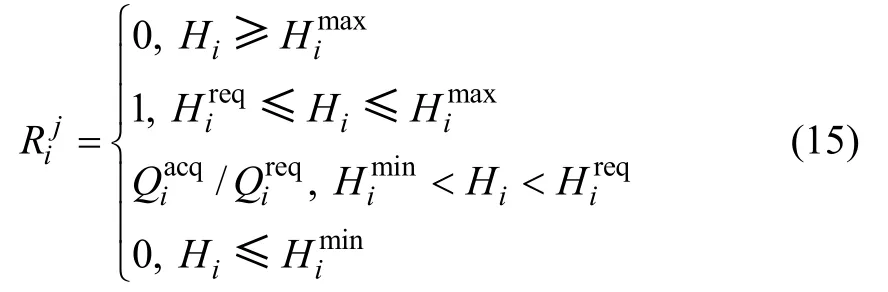
取分析时间为1 a(365 d)，则1 a 中节点的概率可靠度为：

为了体现每个节点对整个供水管网的影响程度，以节点需水量占管网总流量的比例为权值，对整个管网进行综合评价，建立如下数学模型：

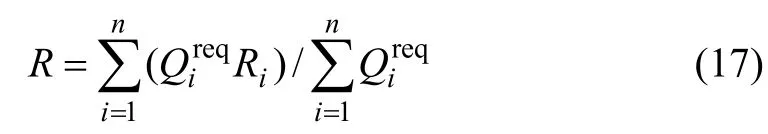
式中：R 为管网水力可靠度；n 为管网节点数；Qireq为节点i 的需水量；Ri为节点i 的概率可靠度。Ri和R分别从局部和整体2 个方面反映了管网的可靠性。

通过以上分析可知：用于研究矿井防尘供水管网的可靠性评价的指标有管段管径、管长、故障率、修复时间以及节点用水量。

2.2 矿井供水管网可靠性评价模型求解流程

基于拟蒙特卡罗法的矿井供水管网可靠性评价基本步骤为：

(1) 运用EPANETH 管网平差软件建立供水管网模型，通过假定管网中的每根管段发生故障，求解对应于每根管段故障状态下的节点可用水量，根据式(15)求得各节点的水力可靠度。

(2) 确定供水管网各管段的故障率λ。统计资料显示，管网发生故障次数的分布规律近似于泊松分布，

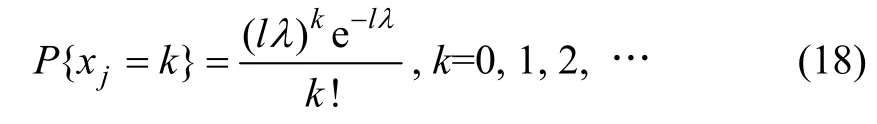
式中：xj为管段j 1 a 内发生故障的次数；l 为管段j的长度，km；λ 为故障率，次/(a·km)。

(3) 产生数量足够多的Sobol 序列。

(4) 进行抽样，观察收敛结果，根据精度要求确定模拟次数，稳定值即为节点的概率可靠度和管网水力可靠度。

(5) 对N 个样本值进行统计分析，估计均值、标准差和其他统计特征。

3 实例应用

将评价模型用于范各庄矿的供水管网，该管网以-124 m 处静压水池为主水源。经过简化，管网中共有20 个节点，19 根管段。运用EPANETH 建模后的各参数信息见图1。管段基本信息见表1。

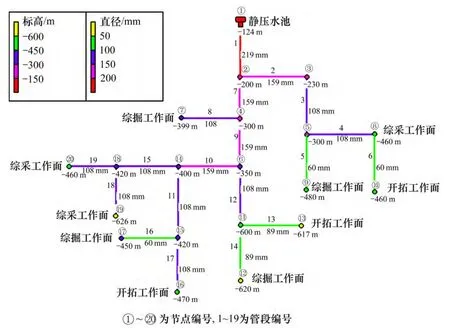
图1 EPANETH 建立管网模型Fig.1 Network model of EPANETH

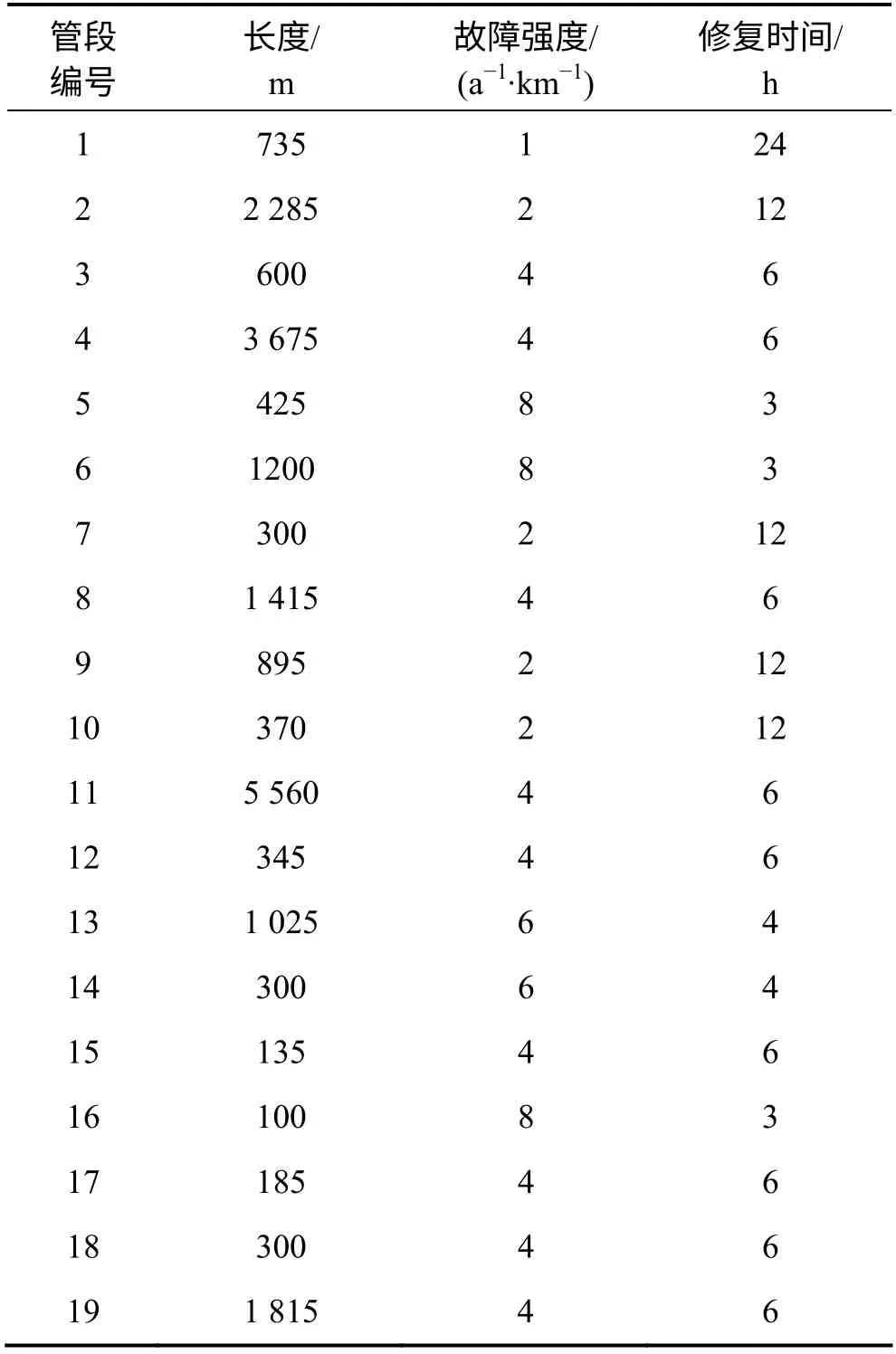
表1 管段基本信息表Table 1 Basic information of pipes

通过EPANETH 对管网中各管段发生故障时的供水情况进行仿真模拟，得到各节点的可用水量，代入式(15)得到对应各管段故障时的节点可靠度。将管网中各节点对应于19 根管段故障状态下的节点可靠度取平均值，具体结果见表2。将管网中各管段发生故障时对应于所有节点的可靠度取平均值，求得管网瞬时水力可靠度，结果见表3。该值反映了管段对管网可靠度的影响程度，是定位关键管段的重要依据。

从表2 可以看出：节点可靠度均值为1 的点为水源节点，其余节点的可靠性都会因为管段发生故障而受到影响。离水源较远的节点可靠度较低，这是因为远离水源的节点依赖的管段比靠近水源的节点要多。

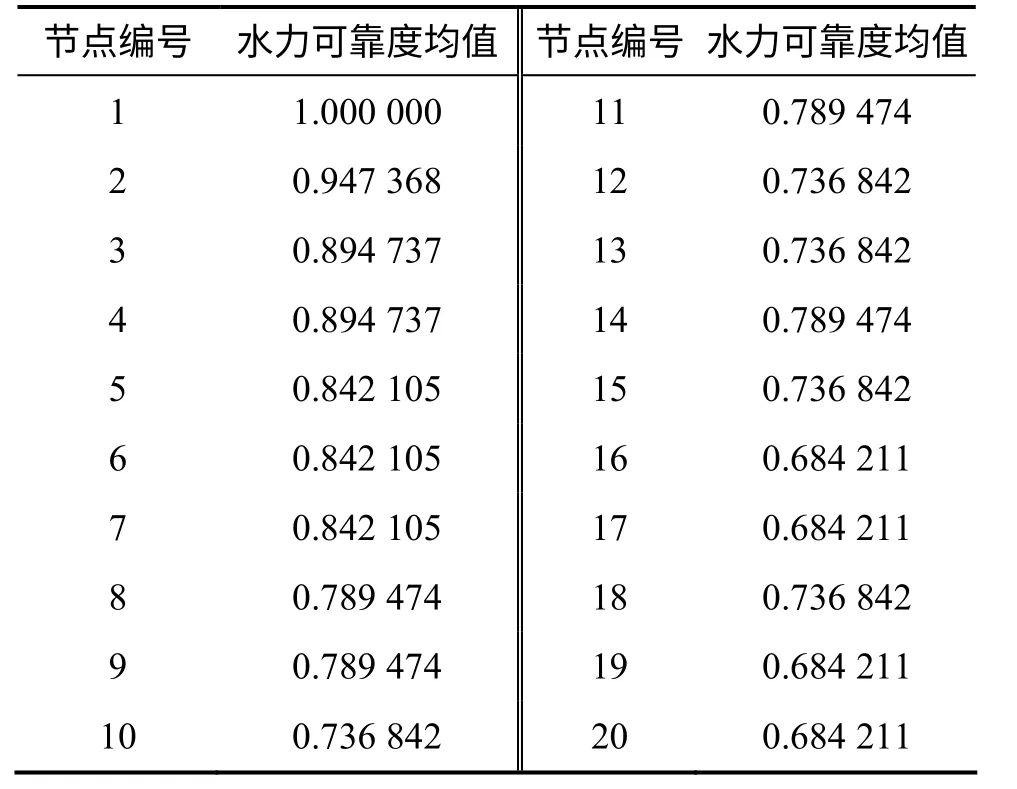
表2 故障时节点水力可靠度均值Table 2 Mean of node hydraulic reliability in trouble

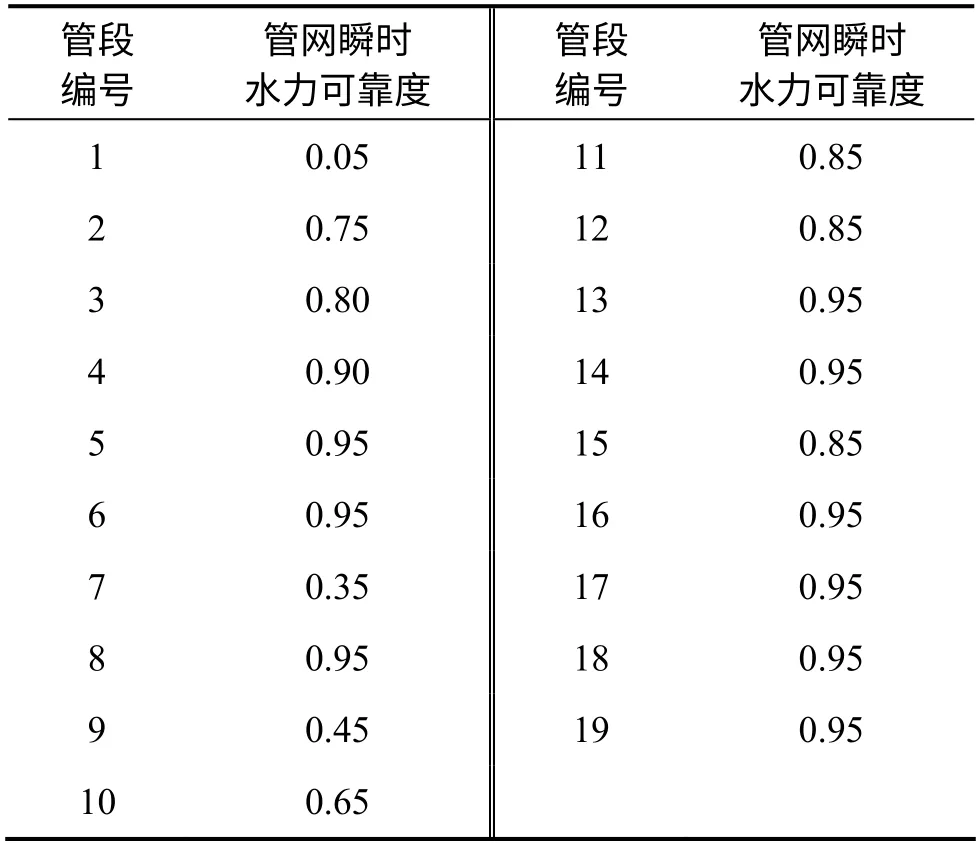
表3 故障时管网瞬时水力可靠度Table 3 Transient hydraulic reliability of network in trouble

从表3 可以看出：管段1 的瞬时可靠度较低，对管网中各节点的可靠性的影响最大，因为该管段为主水源与管网的连接管段，承担着主要的供水任务。从整体上来看，靠近水源的管段一般对管网的可靠性影响较大，远离水源的管段对整个管网的可靠性影响较小。与范各庄矿实际矿井供水管网情况相符。

确定节点的可靠度后，采用拟蒙特卡罗法进行抽样，确定管网中每根管段发生故障的次数，并求得各节点的概率可靠度，再以节点需水量占管网总流量的比例为权值，求得整个管网的可靠度。该过程通过matlab 编程实现。模拟后得到的管网可靠度如图2 所示，其标准差如图3 所示。本文取标准差为0.000 2以下时的结果为管网水力可靠度，根据本例的模拟结果，经过997 次模拟后标准差达到0.000 2，此时的管网可靠度为0.979 169。

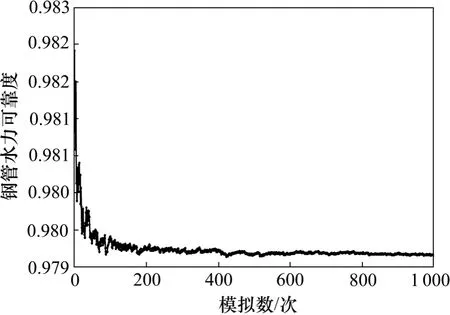
图2 管网可靠度模拟结果Fig.2 Simulation result of network’s reliability

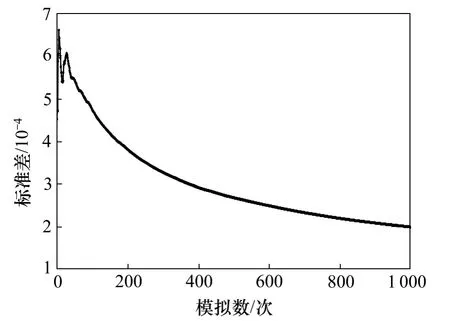
图3 管网水力可靠度模拟标准差Fig.3 Standard deviation of network’s reliability

4 结论

(1) 采用了Sobol 序列作为拟蒙特卡罗法的核心求解部分，提出了矿井防尘供水管网水利可靠性研究的新方法，并将方法运用于实例，为以后管网优化研究提供了参考。

(2) 提高管网水力可靠性的主要方法有降低管段故障率和减少修复时间即加快维修速度。

(3) 供水管网的拓扑结构对管网水力可靠度有着重要的影响，良好的拓扑结构能使管网系统在某些管段发生故障时，断水范围较小，管网的供水能力下降不大。

(4) 对于管网系统中不可修复或难以修复的组件，应该采用可靠性较高的设备，以降低发生故障的可能性。

[1] 张立松, 闫相祯, 杨秀娟, 等. 煤岩破碎失效概率的可靠性分析及分级应用[J]. 煤炭学报, 2012, 37(11): 1823-1828.ZHANG Lisong, YAN Xiangzhen, YANG Xiujuan, et al.Reliability analysis of coal crushing failure probability and its classification application[J]. Journal of China Coal Society, 2012,37(11): 1823-1828.

[2] 肖尊群, 刘宝琛, 乔世范, 等. 重力式挡土墙结构模糊随机可靠性分析[J]. 中南大学学报(自然科学版), 2010, 41(4):1522-1526.XIAO Zunqun, LIU Baochen, QIAO Shifan, et al. Analysis of fuzzy reliability for gravity retaining wall structure[J]. Journal of Central South University (Science and Technology), 2010, 41(4):1522-1526.

[3] 曾晟, 杨仕教, 孙冰, 等. 基于ABAQUS-ANFIS 的露天矿边坡可靠度分析[J]. 煤炭学报, 2006, 31(4): 437-441.ZENG Sheng, YANG Shijiao, SUN Bing, et al. Reliability analysis of open-pit slope based on ABAQUS and ANFIS[J].Journal of China Coal Society, 2006, 31(4): 437-441.

[4] 侯晓东, 蒋仲安. 矿井防尘供水管网失效模糊故障树分析[J].金属矿山, 2008(6): 112-115.HOU Xiaodong, JIANG Zhongan. Fuzzy fault tree analysis of failure of water supply network for mine dust-proofing[J]. Metal Mine, 2008(6): 112-115.

[5] 金溪, 张杰, 高金良, 等. 利用GO 法进行供水管网可靠度计算[J]. 浙江工业大学学报, 2007, 35(6): 682-685.JIN Xi, ZHANG Jie, GAO Jinliang, et al. Calculation of water supply system reliability with GO method[J]. Journal of Zhejiang University of Technology, 2007, 35(6): 682-685.

[6] 桑海涛, 孟稚松, 周真. 矿井防尘供水管网系统的GO 法可靠性分析[J]. 科学技术与工程, 2010, 10(28): 6989-6993.SANG Haitao, MENG Zhisong, ZHOU Zhen. Reliability analysis of water supply network system for mine dust-proofing in GO methodology[J]. Science Technology and Engineering,2010, 10(28): 6989-6993.

[7] 邓建, 边利, 彭怀生. 一种新的蒙特卡罗随机有限元方法[J].中南大学学报(自然科学版), 2006, 37(5): 998-1000.DENG Jian, BIAN Li, PENG Huaisheng. A new Monte-Carlo stochastic finite element method[J]. Journal of Central South University (Science and Technology), 2006, 37(5): 998-1000.

[8] 章征宝, 余云进, 徐得潜, 等. 基于蒙特卡罗法的城市给水管网可靠性分析[J]. 给水排水, 2007, 33(7): 106-110.ZHANG Zhengbao, YU Yunjin, XU Deqian, et al. The reliability analysis of urban water distribution network based on Monte-Carlo method[J]. Water & Wastewater Engineering, 2007,33(7): 106-110.

[9] 李龙云. 蒙特卡罗法在给水管网可靠性评价中的应用[D]. 上海: 同济大学环境科学与工程学院, 2009: 13-14.LI Longyun. Application of Monte-Carlo method in reliability evaluation of water distribution network[D]. Shanghai: Tongji University. College of Environment Science and Engineering,2009: 13-14.

[10] 黄美发, 景晖, 匡兵, 等. 基于拟蒙特卡罗方法的测量不确定度评定[J]. 仪器仪表学报, 2009, 30(1): 120-124.HUANG Meifa, JING Hui, KUANG Bing, et al. Measurement uncertainty evaluation based on quasi Monte-Carlo method[J].Chinese Journal of Scientific Instrument, 2009, 30(1): 120-124.

[12] 朱尧辰. 点集偏差引论[M]. 合肥: 中国科学技术大学出版社,2011: 190-193.ZHU Yaochen. Point set deviation introduction[M]. Hefei:University of Science and Technology China Press, 2011:190-193.

[13] 朱云飞, 罗彪, 郑金华, 等. 基于拟蒙特卡罗方法的进化算法搜索鲁棒最优解的性能提高研究[J]. 模式识别与人工智能,2011, 24(2): 201-204.ZHU Yunfei, LUO Biao, ZHENG Jinhua, et al. Research on increasing the performance of evolutionary algorithm in searching robust optimal solutions based on Quasi-Monte Carlo method[J]. Pattern Recognition & Artificial Intelligence, 2011,24(2): 201-204.

[14] 郭辉, 姬红兵, 武斌. 采用拟蒙特卡罗法的被动多传感器目标跟踪[J]. 西安电子科技大学学报(自然科学版), 2010, 37(6):1042-1046.GUO Hui, JI Hongbing, WU Bin. Quasi-Monte Carlo Gaussian particle filter based target tracking for the multiple passive sensor[J]. Journal of Xidian University (Natural Science), 2010,37(6): 1042-1046.

[15] 罗付岩, 徐海云. 拟蒙特卡罗模拟方法在金融计算中的应用研究[J]. 数理统计与管理, 2008, 27(4): 605-609.LUO Fuyan, XU Haiyun. The applying of Quasi-Monte Carlo methods in financial computation[J]. Application of Statistics and Management, 2008, 27(4): 605-609.

[16] Antonov I A, Saleev V M. An economic method of computing LP-sequences[J]. USSR Comput Math Math Phys, 1979, 19:252-256.

[17] Tabesh M, Tanyimboh T T, Burrows R. Head driven simulation based reliability of water distribution network[J]. Journal of Water Resources Planning and Management, 2001, 127(4):206-209.