金属复合屋面板用硬质聚氨酯泡沫的力学性能

黄 莉， 邓 华， 王 宸

（1.浙江大学空间结构研究中心，浙江杭州310058；2.浙江财经大学工程管理系，浙江杭州310018）

目前，大跨度屋盖结构普遍配套使用轻型金属复合屋面板.此类屋面板通常由上、下面层的压型金属薄板及中间夹芯层组成，其中硬质聚氨酯泡沫是最主要的夹芯材料之一.常规结构设计不考虑屋面系统的作用，但随着分析设计技术的发展，屋面系统对结构受力性能的影响受到越来越多的重视，譬如常规的结构蒙皮效应问题[1].此外，金属复合屋面板的刚度较弱，且其夹芯层一般又为高阻尼材料，因此，在承受并传递屋面风荷载的过程中是否会改变风压的脉动特性并减小屋盖结构的风振效应问题近年来也引起了人们的关注[2].

对于金属复合屋面板常用的硬质聚氨酯泡沫材料，JG／T 314—2012《聚氨酯硬泡复合保温板》只是对其密度、保温性能进行了规定，其力学性能大多简化为各向同性材料来处理，相关研究也只对其发泡方向进行试验测定[3－5].由于配方不同，工业上使用的各种硬质聚氨酯泡沫材料的力学性能差异较大，而直接针对屋面板用硬质聚氨酯泡沫力学性能的研究并不多.文献[6]也只针对建筑结构墙面板中的聚氨酯夹芯在发泡方向的力学性能进行了研究.实际上，硬质聚氨酯泡沫的生产工艺使其发泡方向与涂层面内的力学性能存在差异，因此，本文开展了该材料在发泡方向和涂层面内方向的拉伸和压缩试验.结果发现，这种材料的各向力学性能差异较大，将其看作“横观各向同性”材料更为合理.根据试验数据，对硬质聚氨酯泡沫材料的横观各向同性本构模型基本参数进行了拟合.

1 试验

1.1 试验方法

硬质聚氨酯泡沫由专业厂家提供，密度为42.87kg／m3.为表述方便，定义硬质聚氨酯泡沫的发泡方向（板厚方向）为z向，涂层面定义为x－y平面，板宽方向为x向，板长方向为y向，如图1所示.分别沿x向、y向、x－y面内45°向、z向及x－z面内45°向取样，且取样方向即为试验的加载方向.按照GB／T 9614—1988《硬质泡沫塑料拉伸性能试验方法》和GB／T 8813—1988《硬质泡沫塑料压缩试验方法》制做拉伸、压缩试样，拉伸试样为哑铃形，尺寸如图2所示，厚度为10mm；压缩试样为高40mm，直径25mm的圆柱体.每向试验的有效试样不少于3个.

试验设备采用德国Zwick／Roell万能材料试验机，材料的泊松比采用静态应变仪进行测量.拉伸、压缩试验装置如图3所示，加载速率为4mm／min，试样的伸长量由夹头位置确定，其应力－应变曲线由数据记录仪直接计算、绘制.

1.2 试验结果

图1 金属复合屋面板Fig.1 Metal composite roof panels

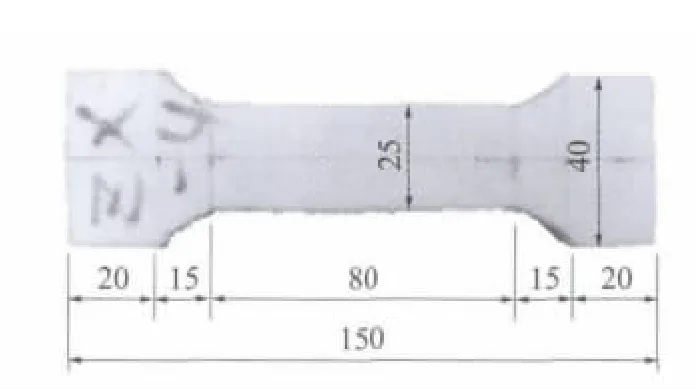
图2 拉伸试样尺寸Fig.2 Tensile specimen（size：mm）

图3 拉压试验装置Fig.3 Tensile and compressive test device

图4为拉伸、压缩试样的破坏模式.拉伸试样的破坏面位于试样中部，破坏面很平整，属脆性破坏.压缩试样无明显的破坏特征，且卸载后试样的压缩变形有少量回弹，回弹表现为“凹”形，即圆柱周边回弹量大于轴心区回弹量.

图4 拉伸、压缩试样的破坏模式Fig.4 Failure pattern of tensile and compressive specimen

图5～9分别为x向、y向、x－y面内45°向、z向及x－z面内45°向的拉伸、压缩应力－应变（σ－ε）曲线.可以看出，各向试样在拉伸断裂破坏前，其应力－应变曲线基本呈线性变化，拉断后应力下降为零；压缩试样的应力应变在加载前期为弹性阶段，应变达到0.050左右时进入屈服段，屈服平台明显，在加载后期（应变约0.400时），应力－应变曲线出现明显上升趋势，这是由于试样在加载过程中被压实，导致其承载力进一步提高.

表1为不同方向的拉伸、压缩基本力学参数，其中：z向的泊松比为μxz；x向的泊松比为μyx；y向的泊松比为μxy；fu为拉伸时极限强度，kPa；fp为压缩时屈服强度，kPa；Et，Ec分别为拉伸、压缩弹性模量，MPa；εu为拉伸极限应变；εp为压缩屈服应变.

图5 x向拉伸、压缩应力－应变曲线Fig.5 Stress－strain relationship of x－direction under tension and compression

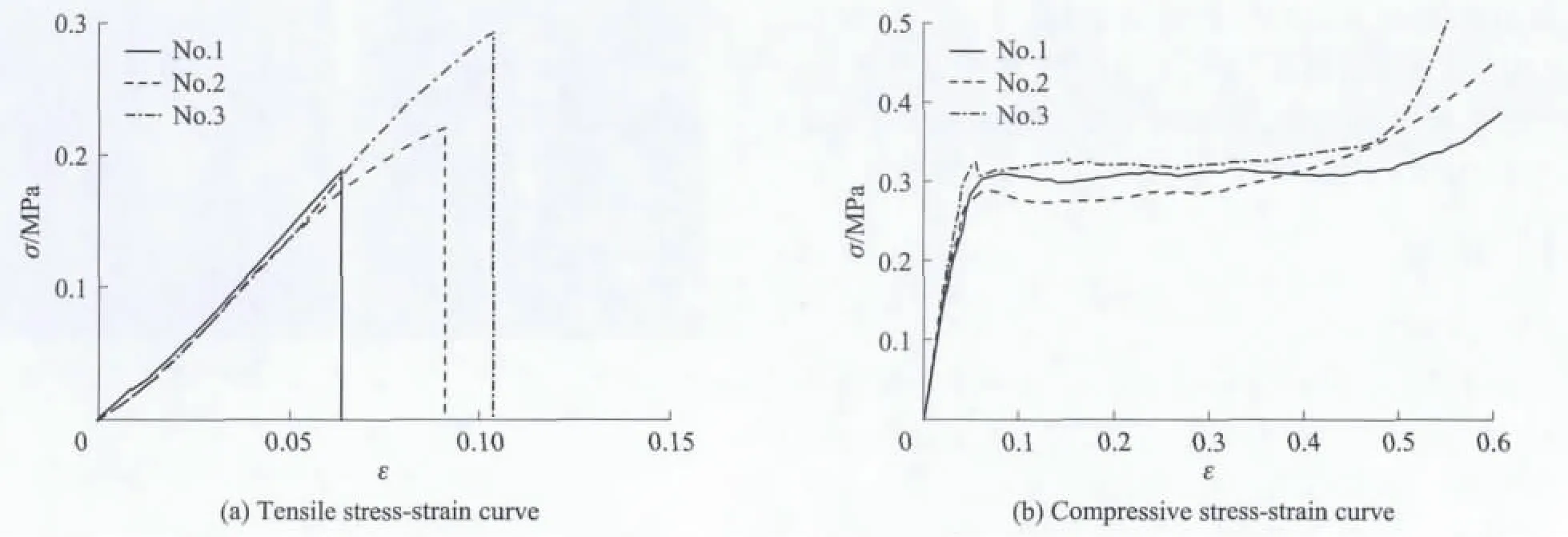
图6 y向拉伸、压缩应力－应变曲线Fig.6 Stress－strain relationship of y－direction under tension and compression

图7 x－y面45°向拉伸、压缩应力－应变曲线Fig.7 Stress－strain relationship of 45°direction in x－y plane under tension and compression

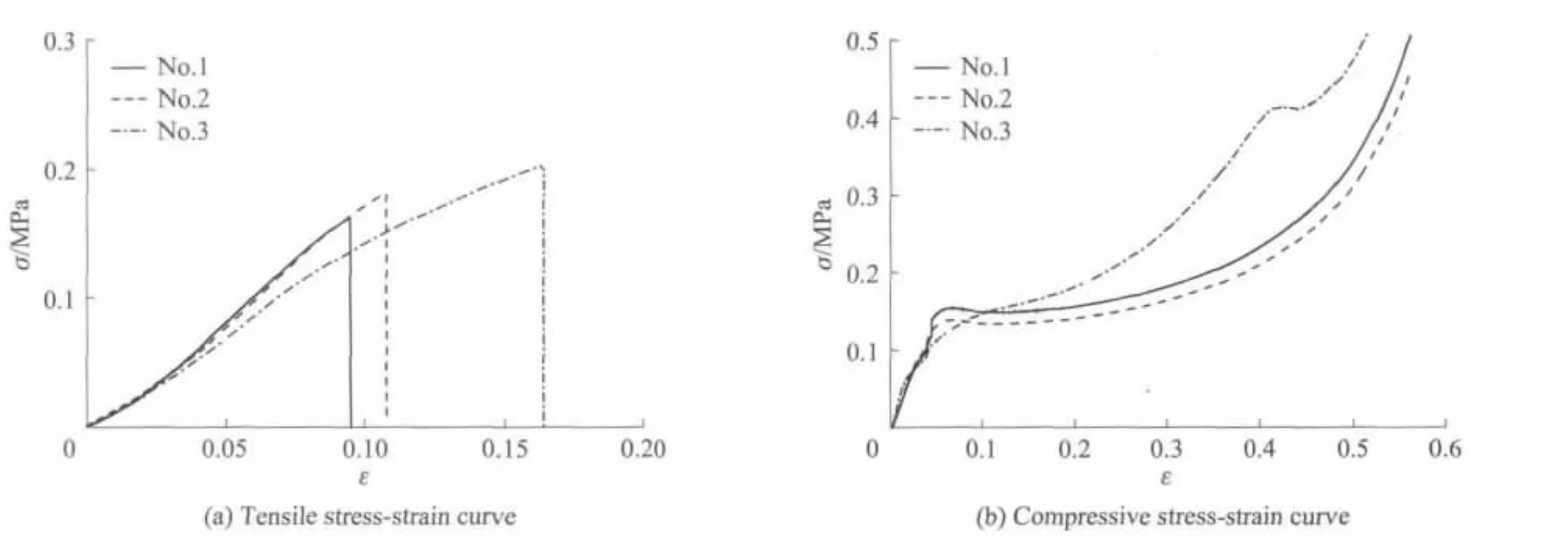
图8 z向拉伸、压缩应力－应变曲线Fig.8 Stress－strain relationship of z－direction under tension and compression

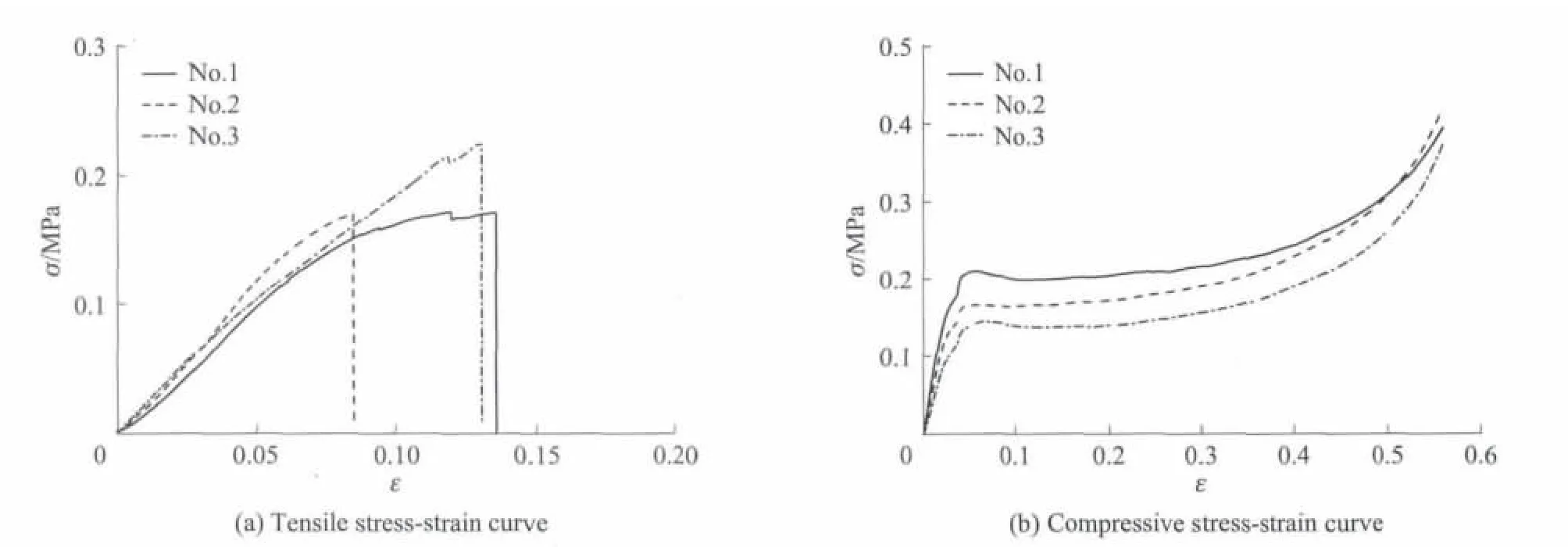
图9 x－z面45°向拉伸、压缩应力－应变曲线Fig.9 Stress－strain relationship of 45°direction in x－z plane under tension and compression

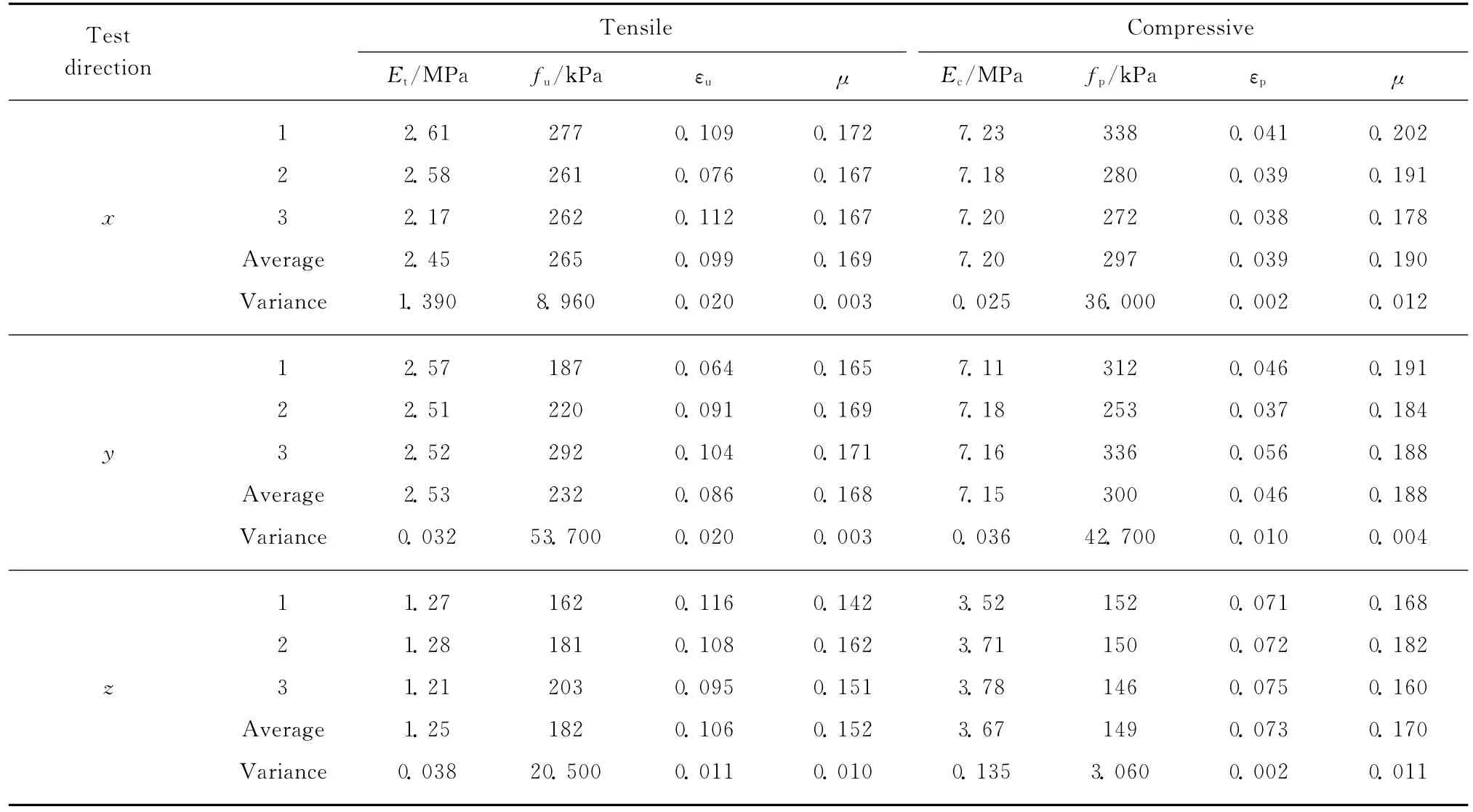
表1 拉、压基本力学参数Table 1 Basic tensile and compressive mechanical parameters

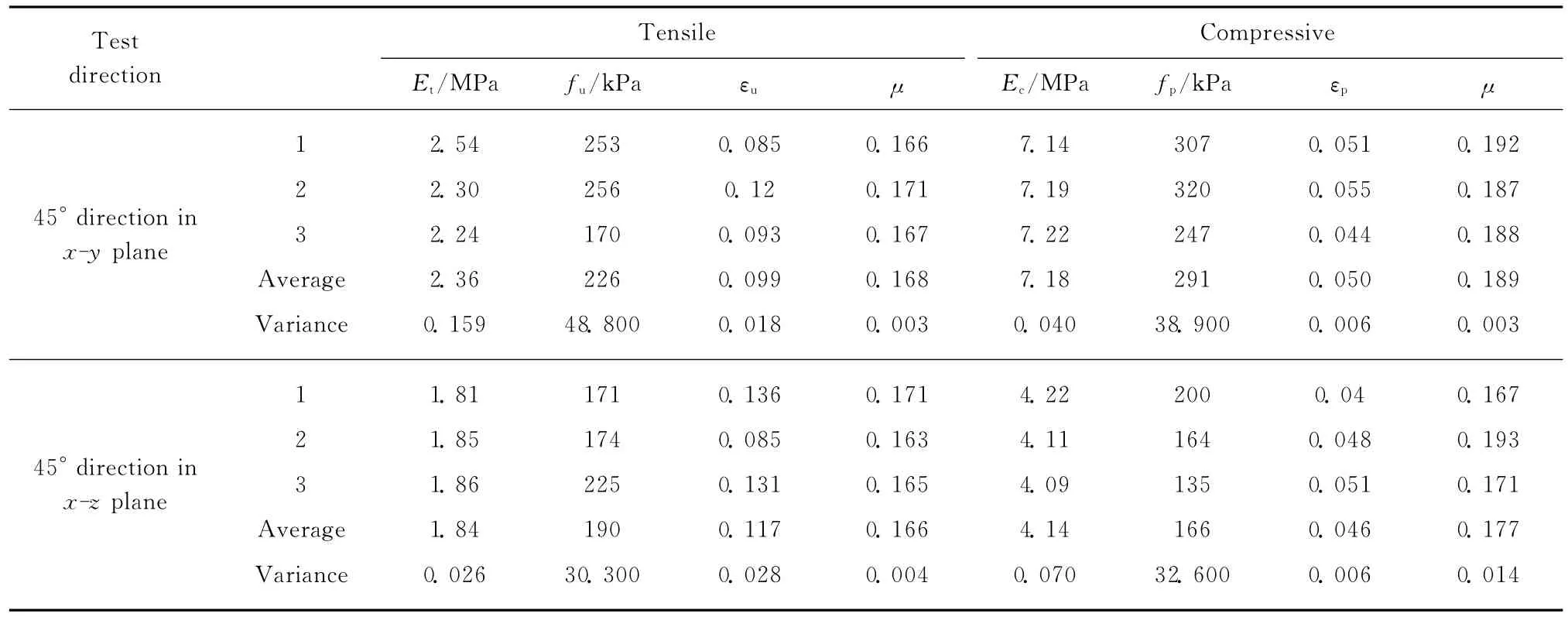
（续表）

1.3 结果分析

由图5～9可见，硬质聚氨酯泡沫材料的拉伸、压缩力学性能相差很大，各向拉伸时，在断裂破坏之前仍处于弹性阶段，其应力－应变曲线可用线弹性模型来模拟.由表1可见，各向拉伸破坏时的极限应变约为0.100，其中最低为0.086，最高为0.117，极限应变的方差最大为0.028（x－z45°向）.各向压缩时的应力－应变曲线在屈服之前也基本为线性变化，屈服应变为0.040～0.050，而极限应变可达到0.600以上.对于压缩应力－应变曲线，在屈服段后期有一个强化过程，可采用常规的三折线模型来模拟.但是，在实际情况下，硬质聚氨酯泡沫材料的应变一般小于0.400，因此可将这种材料的压缩模型简化为理想弹塑性模型.

涂层面内3个方向的拉伸、压缩基本力学参数见表2.由表2可以看出，涂层面内3个方向的力学参数基本一致，且离散性较小，因此可认为涂层面的各向力学性能相同，可采用3向参数的平均值来统一描述.

硬质聚氨酯泡沫材料发泡方向的拉伸、压缩弹性模量分别为1.25，3.67MPa（见表1），其涂层方向约为2.45，7.18MPa（见表2），发泡方向的拉伸极限强度为182kPa，比涂层方向低59kPa，压缩屈服强度为149kPa，也仅为涂层方向的1／2.由此可见，将硬质聚氨酯泡沫看作为各向同性材料并不能正确反映其实际力学性能.根据以上分析及试验结果，建立了硬质聚氨酯泡沫材料单向本构模型，如图10所示，其中拉伸为正、压缩为负.

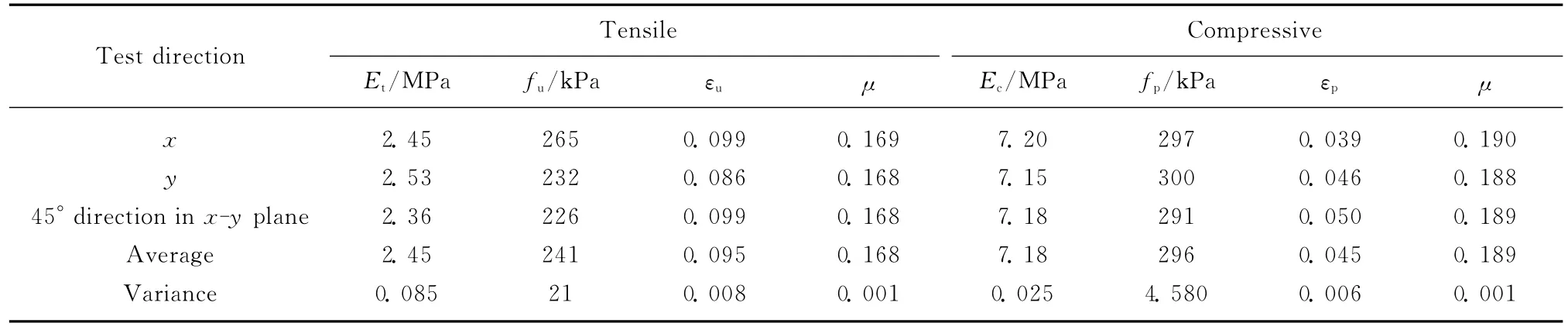
表2 涂层面内各向基本力学参数Table 2 Basic mechanical parameters of coating surface

2 本构关系

材料的弹性应力－应变关系可由广义Hooke定理确定，即：

图10 硬质聚氨酯泡沫材料的单向本构模型Fig.10 Unidirectional constitutive model of rigid polyurethane foam

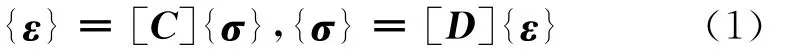
式中：｛σ｝＝[σ1σ2σ3τ23τ31τ12]T；｛ε｝＝[ε1ε2ε3γ23γ31γ12]T；[D]＝[C]－1，[D]为刚度矩阵，[C]为柔度矩阵，二者均为6×6的对称正定矩阵.

根据以上硬质聚氨酯泡沫材料的力学试验结果，可认为其符合横观各向同性材料本构模型[7].将x，y，z方向称为1，2，3，x－y面为各向同性面，则横观各向同性材料存在如下关系：

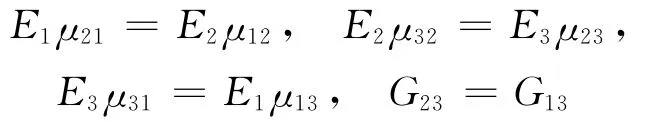
这时，[C]可简化为：

由于G23试验测定困难，文献[8]通过测量1～3面内45°夹角方向（即x－z面内45°向）的弹性模量E45和坐标变换，推导出剪切模量G23，即：

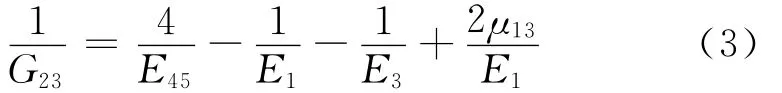
根据表1，2中试验数据，得到硬质聚氨酯泡沫拉伸时的柔度矩阵[Ct]为：

同理，可得到硬质聚氨酯泡压缩时的柔度矩阵[Cc]为：

[Ct]，[Cc]均为正定矩阵，其特征值应大于0.经过计算，[Ct]，[Cc]的特征值[λt]，[λc]为：

均大于0，满足要求.

根据横观各向同性材料本构模型及试验数据，可得到硬质聚氨酯泡沫材料的基本力学参数，如表3所示.

表3 硬质聚氨酯泡沫材料的力学参数Table 3 Mechanical parameters of rigid polyurethane foam

3 结论

（1）拉伸时，硬质聚氨酯泡沫材料为脆性破坏，拉伸极限应变约为0.100，其单向拉伸本构模型可简化为线弹性模型；压缩时，硬质聚氨酯泡沫材料加载前期的应力－应变曲线呈线性变化，当应变为0.040～0.050时出现屈服，且屈服平台明显，在屈服后期为强化阶段，其极限应变大于0.600也不出现明显破坏特征，单向压缩本构模型可简化为理想弹塑性模型.

（2）涂层面内的3个方向力学参数基本一致，且离散性较小，可认为涂层面的各向力学性能相同.发泡方向与涂层方向的力学性能相差较大.将硬质聚氨酯泡沫材料作为各向同性材料并不能正确反映其实际的力学性能.

（3）硬质聚氨酯泡沫材料符合横观各向同性材料模型.

[1] 叶继红，刘志凌.冷成型钢住宅结构的蒙皮效应研究[J].应用力学学报，2009，26（3）：594－599. YE Jihong，LIU Zhiling.Skin diaphragm effects on cold－formed steel structure[J].Chinese Journal of Applied Mechanics，2009，26（3）：594－599.（in Chinese）

[2] 丁阳，齐麟，赵奕程，等.考虑屋面板自振效应和流固耦合效应的大跨度空间结构风振系数[J].建筑结构学报，2008，29（5）：101－106. DING Yang，QI Lin，ZHAO Yicheng，et al.Wind vibration coefficient of long－span spatial structures with self－oscillating of roof and fluid structure coupling effect[J].Journal of Building Structures，2008，29（5）：101－106.（in Chinese）

[3] ALONSO M V，AUAD M L，NUTT S.Modeling the compressive properties of glass fiber reinforced epoxy foam using the analysis of variance approach[J].Composites Science and Technology，2006，66（13）：2126－2134.

[4] WOUTERSON E M，BOEY F Y，HU X，et al.Effect of fiber reinforcement on the tensile，fracture and thermal properties of syntactic foam[J].Polymer，2007，48（11）：3183－3191.

[5] 秦培成，查晓雄，于航.聚氨酯硬质泡沫材料本构研究及其在夹芯板中的应用[J].工业建筑，2008，38（4）：77－81. QIN Peicheng，ZHA Xiaoxiong，YU Hang.Study on polyurethane foam material constitutive relation and its application in sandwich panels[J].Industrial Construction，2008，38（4）：77－81.（in Chinese）

[6] 范钦珊.材料力学[M].北京：高等教育出版社，2000：3－13. FAN Qinshan.Mechanics of material[M].Beijing：Higher Edu－cation Press，2000：3－13.（in Chinese）

[7] 丁皓江.横观各向同性弹性力学[M].杭州：浙江大学出版社，1997：17－22. DING Haojiang.Elastic mechanics of transversely isotropic[M].Hangzhou：Zhejiang University Press，1997：17－22.（in Chinese）

[8] 张晓霞，周柏卓.正交各向异性材料弹性本构关系分析[J].航空发动机，1997（1）：20－25. ZHANG Xiaoxia，ZHOU Bozhuo.Analysis on the elastic constitutive relationship of orthotropic material[J].Aircraft Engine，1997（1）：20－25.（in Chinese）