一类广义凸集值映射优化问题弱有效解的最优性条件

宋永明，胡 君

(1.昆明铁路机械学校，云南 昆明 650208;2.云南省国有资产监督管理委员会，云南 昆明 650031)

一类广义凸集值映射优化问题弱有效解的最优性条件

宋永明1，胡 君2

(1.昆明铁路机械学校，云南 昆明 650208;2.云南省国有资产监督管理委员会，云南 昆明 650031)

在序线性拓扑空间中定义了近似C－次类凸映射的概念，然后应用向量拓扑空间中的凸集分离定理建立了近似C×D－次类凸的择一定理，最后运用此定理获得了弱有效解意义下的集值向量优化问题的最优性条件.

集值映射;近似C－次类凸;择一定理;弱有效解;最优性条件

0 引言

随着最优化理论研究的不断深入，及其在非线性系统、控制论、广义方程及变分问题等领域中的广泛应用，其面临越来越多的集值函数问题.近年来，科研人员对集值优化理论的研究已取得了比较丰富的成果，例如，文献［1］将文献［2］的广义凸函数推广到广义锥次似凸集值映射，文献［3］在向量拓扑空间中，在拓扑内部非空的条件下，定义了一种新的广义凸向量集值映射，建立了此映射的择一定理及广义凸规划问题的最优性条件，文献［4］在向量拓扑空间中，定义了一种新的凸向量集值映射，并研究了Lagrangian对偶定理和标量化定理.在此基础上，本研究在拓扑向量空间中定义了近似C-次类凸的概念，建立了择一定理，并利用此定理，在拓扑向量空间中探讨了带广义等式和不等式约束的向量优化问题弱有效解的最优性必要条件和充分条件，推广了文献［1-5］中的部分结果.

1 预备知识

设X非空集合，Y，Z是线性拓扑空间，C和D分别是Y和Z中的拓扑内部非空的闭凸点锥.用Y*和Z*分别表示Y和Z的拓扑对偶空间，称C*={y*∈Y*:〈y，y*〉≥0，∀y∈Y+}为C的对偶锥，C*i={y*∈Y*:〈y，y*〉＞ 0，∀y∈Y+{0Y}}为C的严格对偶锥，其中，〈y，y*〉表示线性泛函y*在点y的函数值.集值映射，g:X→2Y，h:X→2Z，集值映射，H=(g，h):X → 2Y×Z.设，x ∈ C，y*∈ Y*，〈g(x)，y*〉≥ 0⇔〈y，y*〉 ≥ 0，∀y ∈ g(x);〈g(C)，y*〉≥0⇔〈g(x)，y*〉≥0，∀y∈ C.

定义1［4］设E⊂X为一非空子集，集值映射，F:E→ 2Y，称为近似C-次 类凸的，如果是凸的.

注:近似C-次类凸是C-次类凸的推广.

2 择一定理

定理1 设intC≠Ø，intD≠Ø，H在X上是近似C×D-次类凸的，则下列叙述有且只有一个成立:

①存在x∈X，使g(x)∩(-intC)≠Ø，h(x)∩(-intD)≠Ø.

②存在c*∈C*，d*∈D*，(c*，d*)≠ (0C，0D)，使得，

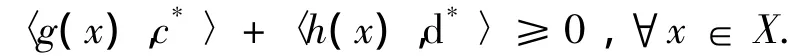
证明 假设①、②都成立，则存在x∈X，使得，

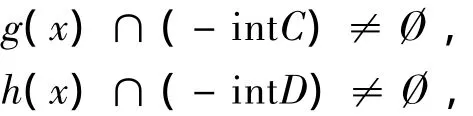
即，∃c1∈g(x)∩(-intC)，d1∈h(x)∩(-intD).由题设知，c*∈C*，d*∈D*可得，〈c1，c*〉+〈d1，d*〉＜0，此与②矛盾，故①和②不能同时成立.

下面证明如果①不成立，那么②成立.假设，

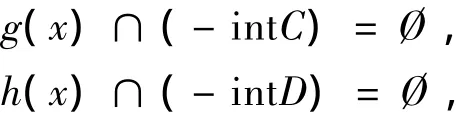
容易得到，

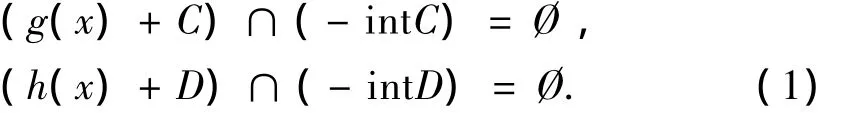
因为，C，D是闭凸锥，所以，

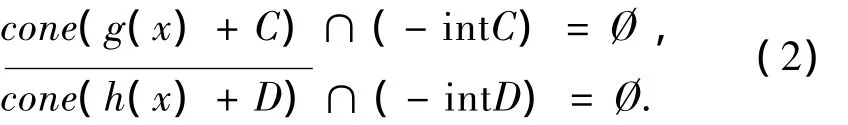
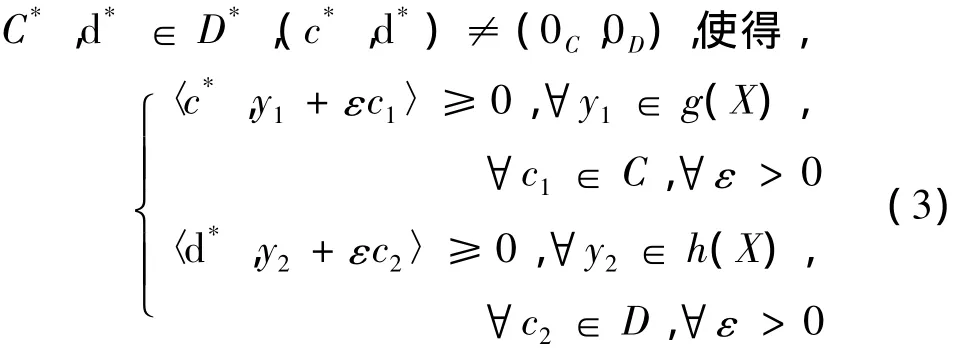
所以，

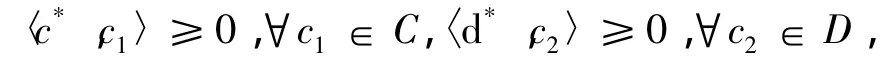
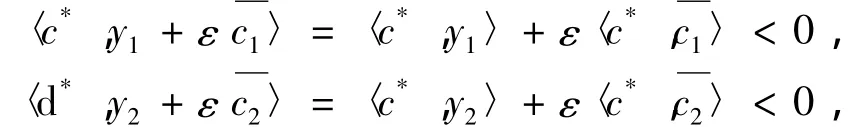
此与式(3)矛盾.于是，c*∈ C*，d*∈ D*，(c*，d*)≠ (0C，0D).

在式(3)中令ε→0，可得到，〈c*，y1〉≥0，∀y1∈ g(X)，〈d*，y2〉≥0，∀y2∈ h(X).

从而证明了②是正确的.

3 最优性条件

设集值映射，f:X→2W，g:X →2Y，h:X→2Z，E，C，D分别是W，Y，Z中的拓扑内部非空的闭凸点锥，令，V=E × C ×D.令，U=W ×Y ×Z，G=(f，g，h):X→2U，称G在X上是近似C×D-次类凸的，如果G=((f，g)，h)在X上是近似C×D-次类凸的，即，cl(cone(F(X)+V))是凸的.

考虑优化问题，

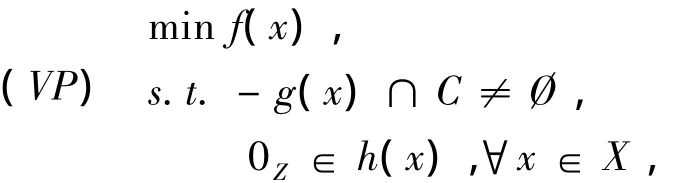
用K表示(VP)的可行集，

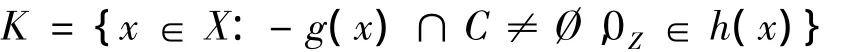
定义2 x0∈K称为(VP)的弱有效解，如果∃w0∈f(x0)，对∀x∈K，∀w∈f(x)，使得w0-w∈intE，(x0，w0)则称为(VP)的弱有效元.

由定义可得下列命题，

命题 1 设 x0∈ K，w0∈ f(x0)，(x0，w0)是(VP)的弱有效元，当且仅当，(w0-f(K))∩intE=Ø.

定理2 设x0∈K，w0∈f(x0)，且满足:

①(x0，w0)是(VP)的弱有效元;

②G=(f-w0，g，h)在K上是近似C×D-次类凸的，则，

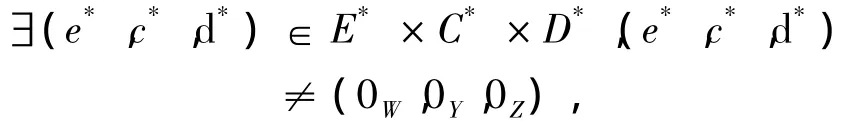
使得，

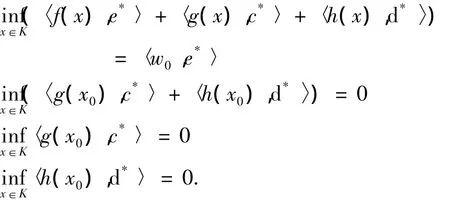
证明 由条件①及命题1知，

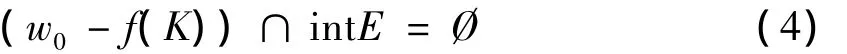
于是，-G(x)∩(intE，intC，intD)= Ø，∀x∈K.若不然，则，

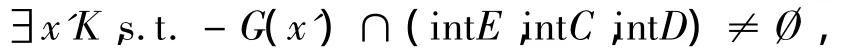
于是，

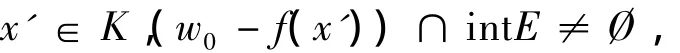
此与式(4)矛盾.从而，由条件②及定理1知，

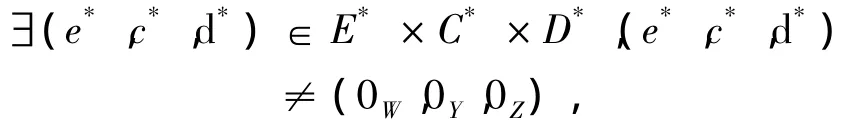
使得，

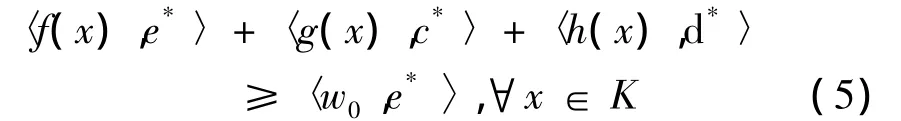
由x0∈K知，∃y∈g(x0)，s.t.-y∈C，从而，〈y，c*〉≤0，取 x=x0，由0Z∈ h及式(5)可得，

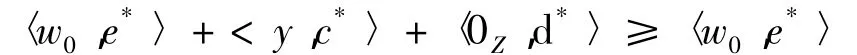
故〈y，c*〉≥0.于是，

因此，

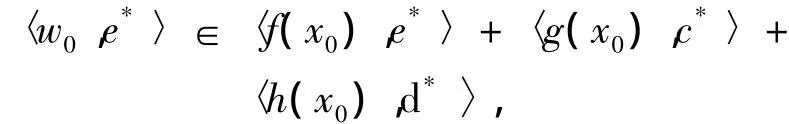
从而由式(5)得到，

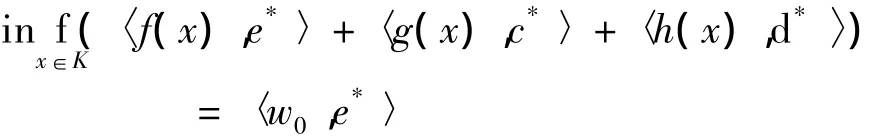
取x=x0代入式(5)，可得，

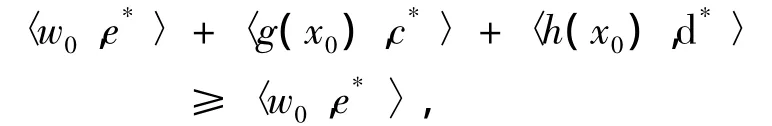
即是，

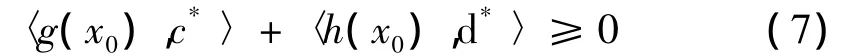
从而由式(6)和0Z∈h(x0)可得，

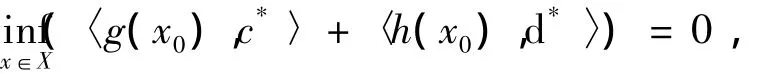
由式(7)和0Z∈h(x0)可得，

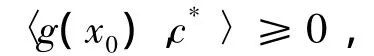
由式(6)可得，

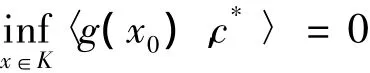
由式(6)和(7)可得，〈h(x0)，d*〉≥0，由0Z∈h(x0)得，

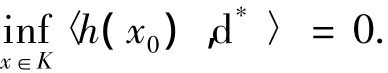
定理3 设x0∈K，且∃w1∈f(x0)，e*∈E*i，c*∈C*，d*∈D*，使得，

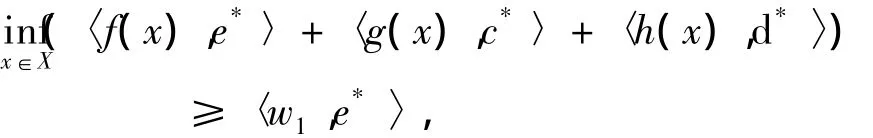
则x0是(VP)的弱有效解.

证明 由题设可知，∃w1∈f(x0)，e*∈E*i，c*∈C，d*∈D*，使得，

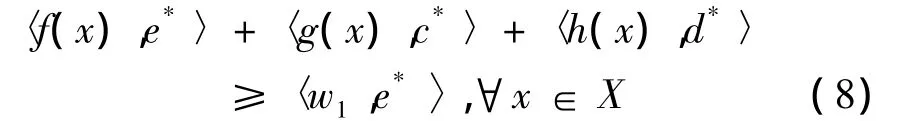
假设x0不是(VP)的弱有效解，则由命题1可知，对于题设中的w1，∃x'∈K，使得，

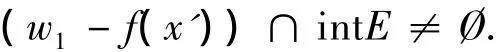
于是，

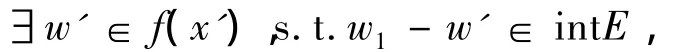
由e*∈E*i得，

由 x'∈K得，∃y'∈g(x')，s.t.-y∈C，且，0Z∈ h(x')，故，

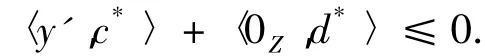
由式(9)得，

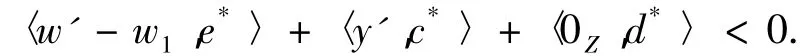
此与式(8)矛盾，故x0是(VP)的弱有效解.

［1］Huang Y W.Generalized cone-subconvexlike set-valued maps and applications to vector optimization［J］.Journal of Chongqing university(English Edition)，2002，1(2):67 －71.

［2］Frenk J B G，Kassay G.On class of generalized convex functions，Gordan-Farkas type theorems，and Lagrangian duality［J］.Journal of Optimization Theory and Applications，1999，102(2):315－343.

［3］Illes T，Kassay G.Theorems of the alternative and optimality conditions for convexlike and general convexlike programming［J］.Journal of Optimization Theory and Applications，1999，101(2):243－257.

［4］Yang X M，Li D，Wang S Y.Near-subconvexlikeness in vector optimization with set-valued functions［J］.Journal of Optimization Theory and Applications，2001，110(2):413 －427.

［5］王其林.一类广义凸集值映射优化问题弱有效解的最优性条件［J］.四川师范大学学报(自然科学版)，2007，30(5):556－559.

［6］宋永明.一类集约束下的向量极值问题的最优性条件［J］.重庆工学院学报，2008，22(2):60 －63.

Optimality Conditions of Weak Efficient Solutions for Optimization Problems of One Class of Generalized Convex Set-valued Mapping

SONG Yongming1，HU Jun2
(1.The Railway Mechanical School of Kunming，Kunming 650208，China;2.State-owned Assets Supervision and Administration Commission of Yunnan Provincial People’s Government，Kunming 650031，China)

This paper defines the concept of nearly C-subconvexlike function in topological vector spaces，and then establishes the alternative theorem of the nearly-subconvexlike function by the convex set separation theorem.Finally，using the alternative theorem，we obtain the optimality conditions of weak efficient solutions for the optimization problems with generalized equality and inequality constraints.

set-valued mapping;nearly C-subconvexlike function;theorem of the alternative;weak efficient solution;optimality condition

O224

A

1004－5422(2014)01－0026－03

2013-12-05.

宋永明(1978—)，男，硕士，讲师，从事最优化理论与应用研究.