基于数字地形图的三维地形生成方法研究

齐 榕，齐 敏，李 珂

（西北工业大学 陕西 西安 710129）

地形是自然界非常复杂但又非常重要的景物，任何虚拟场景的描述都离不开地形的模拟绘制，地形模型的生成及可视化已成为一个十分活跃的研究领域，应用也越来越广泛[1]。在军事领域，大量应用于飞行驾驶模拟训练、战场作战模拟等领域中，显示出了相当大的视觉感官优势和极强的生命力。在民用领域，广泛应用到地理信息系统、汽车驾驶仿真系统、电子沙盘的制作、3D游戏和森林防火系统等。

地形图指的是地表起伏形态和地物位置、形状沿铅垂线方向在水平面上的投影图[2]。传统地形图一般采用手工方法进行地表信息的采集、处理和表达，随着计算机科学与计算机图形学的发展并引入到地图学领域，地形图以数字形式存储于计算机，并将数字地形晕渲图、等高线以及各种标注信息综合显示，提高信息量和可读性。数字地形图已成为最新、最现代化的地图品种。

在许多视景仿真中需要符合实际地理特征的地形，而现有的三维地形生成方法都存在一定的缺点[3-6]。本文利用数字地形图上的数字地形晕渲图信息可生成符合实际地理特征的三维地形。首先对数字地形图进行预处理，得到信息完整的数字地形晕渲图，而数字地形晕渲图是在数字高程模型的基础上通过晕渲得来[7]，因此可由数字地形晕渲图进行地形高度的恢复，最后使用三维显示技术生成逼真的三维地形。

1 数字地形图预处理

本文使用的数字地形图如图1所示，该地形图上有等高线、河流、铁路公路以及标注等要素，因此在用数字地形晕渲图对高度进行恢复之前要进行预处理，首先要结合各要素的特点，去除各要素，然后对空白的部分可采用图像修复技术进行填充。分析各要素的特点，标注、河流和公路铁路的检测可使用HIS模型，等高线和和周围颜色像素差别较大，过渡明显，具有3个像素左右的宽度，可使用边缘检测的算法并结合闭运算，用平滑滤波技术去除噪声，各要素检测后如图2所示。在地形图各要素去除后，需要对去除的部分进行填充，可使用图像修复的方法获得完整信息的数字地形晕渲，如图3所示。

2 地形高度恢复

数字地形晕渲图是在数字高程模型的基础上通过晕渲得来[7]，通过分析，数字地形晕渲图的光照模型可近似为：

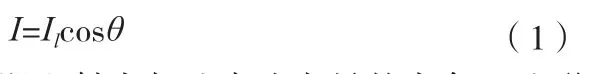
其中θ为入射角，即入射光与地表法向量的夹角。地形各部位所获得的光照为仅以Lambert余弦定理计算漫反射光强来表示地表各部分获得的光照[8]，这与由明暗恢复形状（Shape from Shading，SFS）算法设定的假设条件是一致的[2]，因此可将SFS算法应用于地形的高度恢复中。

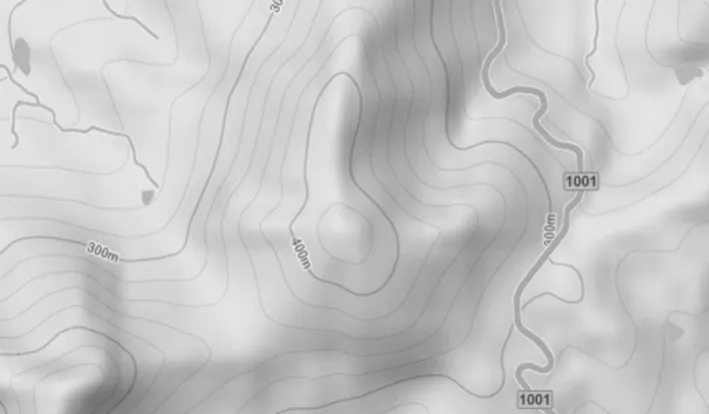
图1 数字地形图Fig.1 Digital terrian map

图2 要素检测图Fig.2 Elements detection map

图3 数字地形晕渲图Fig.3 Digital hill-shading map

2.1 SFS算法研究

SFS原理是利用单幅图像的明暗变化来恢复物体表面各点的相对高度[9],传统SFS算法认为物体表面的图像亮度I仅由该点的光源入射角θ的余弦决定[10]，物体表面图像亮度就可以表示为：

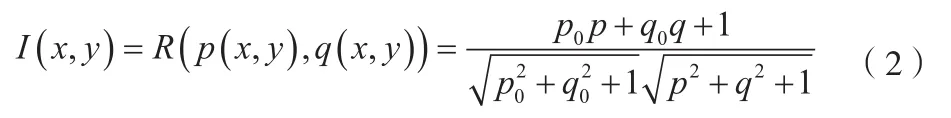
其中，(-p0,-q0,1)为光源方向，(p,q)为梯度，I(x,y)表示归一化的亮度图像，R(p,q)是反射函数。由于上式（2）一个方程中有两个未知量，因此由该模型确定的SFS问题是病态的，即没有唯一解，因此需要引入其他约束条件。

目前SFS算法有很多，考虑到大多数的视景仿真需要满足实时性的要求，线性化方法可满足要求，选择其中的Tsai[11]的方法来恢复地形高度。若物体表面高度表示为Z=Z(x,y)，Tsai的方法用下式离散逼近p和q：

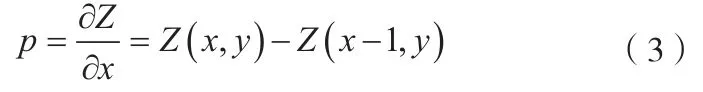
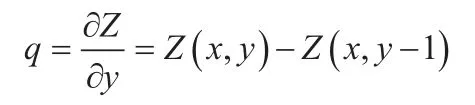
上式中使用了一阶偏导，即默认表面光滑。通过上式，图像辐照度方程可写为：

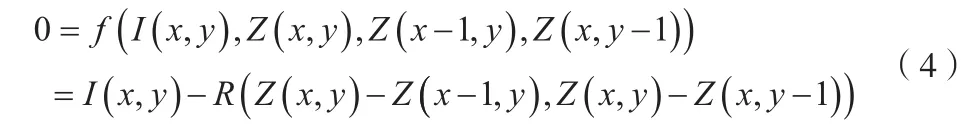
对于图像上的固定点(x,y)和给定的图像强度I，将式（4）进行Talor展开：

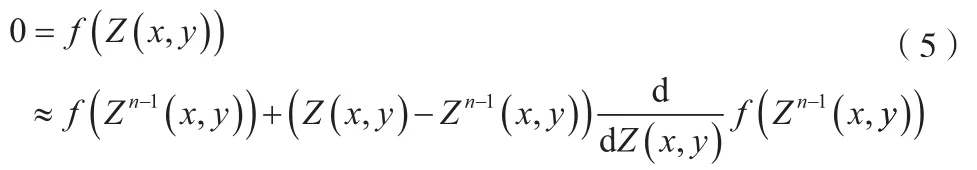
当Z(x,y)=Zn(x,y)，第n次迭代的深度为：

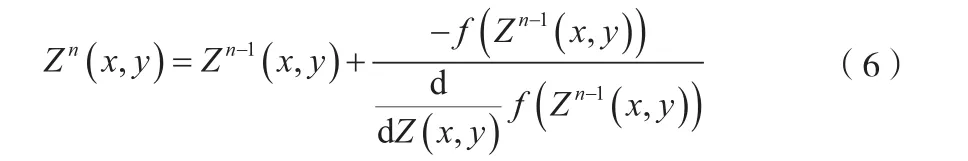
其中：

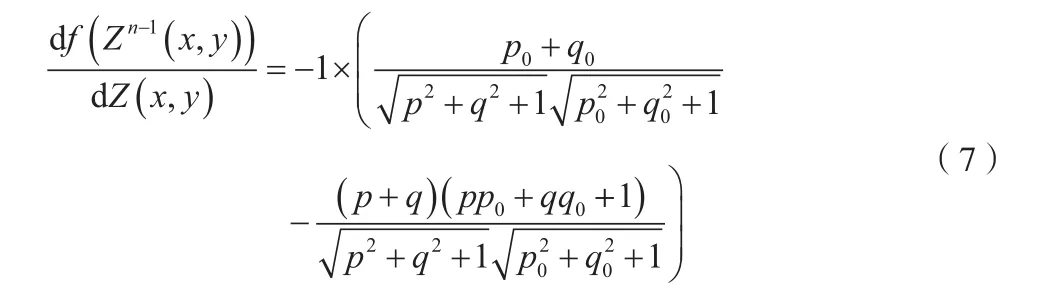
2.2 地形高度恢复实现

假设地形图上所有像素的初始值为Z0(x,y)=0，地形高度恢复过程可归纳为：

1)估计光源方向。

2)求Z1(x,y)，为：

3)通过式（3）求得p和q，按照式（5）求Zn(x,y)：

4)重复步骤3），直到满意的结果为止。

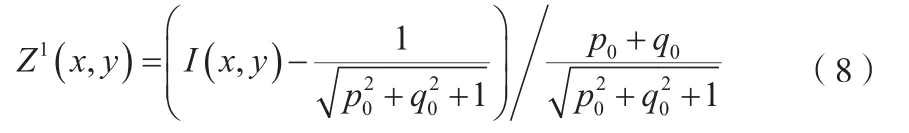
3 实验结果与分析

恢复出的地形高度图为图4所示，根据等高线判断山脊的部分，在恢复出的高度地形图中的地方基本吻合，可以看出恢复出的地形轮廓符合原始地形的特点。由SFS恢复出的地形高度为相对高度，因此可直接用于视景仿真中。剔除噪声，并使用纹理映射技术生成逼真的三维地形如图5所示。

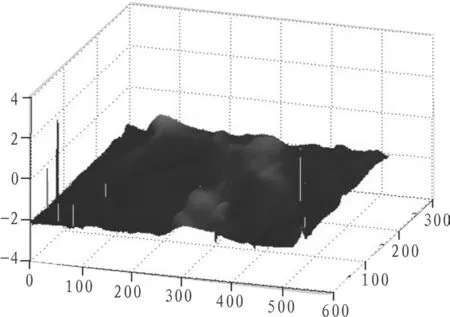
图4 地形高度示意图Fig.4 Terrain height map

图5 真实感三维地形Fig.5 Realistic 3D terrain

为了进一步验证该方法的有效性，使用ASTER GDEM数据进行对比，ASTER GDEM数据记录的是地形的三位信息，分辨率为90 m，而本文使用的数字地形图的分辨率为4 m。首先用ASTER GDEM的最大值和最小值对恢复出的相对高度进行线性映射，得到实际高度之后再和ASTER GDEM数据进行对比。通过分析，向阳区域的误差较小，背阴区的误差相对较大，但基本可以反映出真实地表的起伏轮廓，因此将SFS方法应用于基于数字地形图的三维地形生成是有效的，可广泛应用与三维视景仿真中。

4 结 论

文中利用数字地形图，通过预处理技术，去除各种要素并修复后，得到具有完整信息的数字地形晕渲图，并将SFS方法应用于地形高度的恢复中，通过线性映射得到实际地形的高度信息，最后实现地形的三维显示。实验结果表明该方案的正确性及可行性，可广泛应用于三维视景仿真中。

[1] 和平鸽工作室.OpenGL高级编程与可视化系统开发高级编程篇[M].2版.北京: 中国水利水电出版社, 2006.

[2] 施祖辉. 地貌晕渲法[M]. 北京: 测绘出版社,1979.

[3] Hoppe H.Progressive meshes [C]//Computer Graphics Proceedings,Annual Conference Series.New Orleans:ACMPress,1996:90-108.

[4] Tsung-Pao Fang,Les A Piegl. Algorithm for constrained Delaunay triangulation [J].The VisualComputer.1994(10):255-265.

[5] Musgrave K, Kolb C,Mace R.The synthesis and rendering of eroded fractal terrains [J].Computer Graphics,1989(23):41-50.

[6] Lewis J P.Generalized Stochastic Subdivision[J].ACMTransactions on Graphics 1987,6(3):167-190.

[7] 李少梅, 阚映红, 陈艳丽, 等. 数字地貌晕渲光照模型研究[J].测绘科学技术学报,2010,27(1):57-60.LI Shao-mei,KAN Ying-hong,CHEN Yan-li,et al.Research on illumination model of digital relief shading[J].Journal of Geomatics Science and Technology,2010,27(1): 57-60.

[8] 宋丽梅. 基于单幅实时测量图像的三维形貌恢复技术研究[D].天津: 天津大学,2004.

[9] Horn B K P,Brooks MJ.Shape from shading[M].MA:MIT Press, 1989.

[10] 廖熠,赵荣椿,从明暗恢复形状(SFS) 的几类典型算法分析与评价[J]. 中国图象图像形学报,2001,6(10): 953-961.LIAO Yi,ZHAO Rong-chun.Analysis and evaluation of several typical SFS algorithms[J].Journal of Image and Graphics,2001,6(10): 953-961.

[11] Tsai P S,Shah M.Shape from shading using linear approximation[J].Image and Vision Computing Journal,1994,12(8):487-498.