地面出入式盾构隧道修正惯用法计算参数研究
张银屏
(上海市城市建设设计研究总院,上海 200125)
0 引言
修正惯用法是盾构隧道衬砌设计中最常用的简化计算方法[1],抗弯刚度折减系数η和弯矩调整系数ξ是计算中应用到的2个关键参数。对于常规埋深盾构隧道,根据经验采用修正惯用法分析衬砌内力变形时的参数取值已有大量研究,DGJ 08—11—2010《地基基础设计规范》建议衬砌抗弯刚度效率系数η取值范围0.6~0.8,弯矩调整系数ξ取值范围0.3~0.5[2]。
地面出入式盾构隧道由一台适用于超浅覆土施工的盾构沿设计轴线从道路一端自地面始发,在超浅覆土工况下掘进,逐渐过渡到常规覆土后由地面接收。该方法可避免常规盾构隧道工作井和引道明挖施工占用大量施工场地所带来的一系列问题。但由于盾构直接从地面始发,其覆土极浅(甚至为负值),隧道衬砌荷载模式与常规深埋隧道不同,受力亦有所不同[3]。超浅埋盾构隧道若采用修正惯用法进行内力计算,因衬砌接头刚度较小,衬砌抗弯刚度效率系数η需相应减小,弯矩调整系数ξ相应增加。
盾构隧道壳-弹簧模型可充分考虑管片间接头的影响,相对简单的修正惯用法更接近实际情况。Oriol Arnaud[4]认为盾构管片之间因相互接触存在显著的空间效应,并对三维壳-弹簧有限元模型与平面模型空间效应产生的影响进行对比分析;朱伟[5]运用壳-弹簧模型与梁-弹簧模型分别对衬砌管片通缝和错缝拼装进行对比,并分析了衬砌管片错缝拼装下2种模型计算结果的异同,对盾构管片的设计具有一定的指导作用;苏宗贤等[6]提出了地层-结构模式下的壳-弹簧-接触计算模型,该模型较好地考虑了管片间接缝处的挤压作用、管片接头刚度的影响、管片与围岩的共同变形以及封顶块的近似插入角。因此,能有效地模拟盾构隧道管片衬砌的复杂受力状态。
本文基于壳-弹簧模型建立三维有限元模型,考虑接头抗弯刚度与接头轴力弯矩的非线性关系,对地面出入式超浅埋盾构隧道修正惯用法的关键计算参数η和ξ的取值进行分析研究,给出超浅埋情况下计算参数η和ξ的建议取值,以扩展修正惯用法的使用范围。
1 地面出入式盾构隧道的荷载分布模式
地面出入式盾构隧道从地面始发,隧道覆土厚度由负值逐渐过渡成正值,隧道逐步钻入地面以下,隧道衬砌的荷载模式随着覆土厚度的变化也在不断变化。隧道完全进入土体后,荷载与常规盾构隧道相同(见图1),所受荷载主要有上部及侧向的土压力、周边水压力及自重。在负覆土阶段(见图2),隧道上部没有覆土,上部土荷载为零,拱肩部分土体形成三角形竖向荷载,隧道埋入土中部分受到相应的三角形土体侧向荷载,隧道位于地下水位以下部分则承受相应的径向水压力。
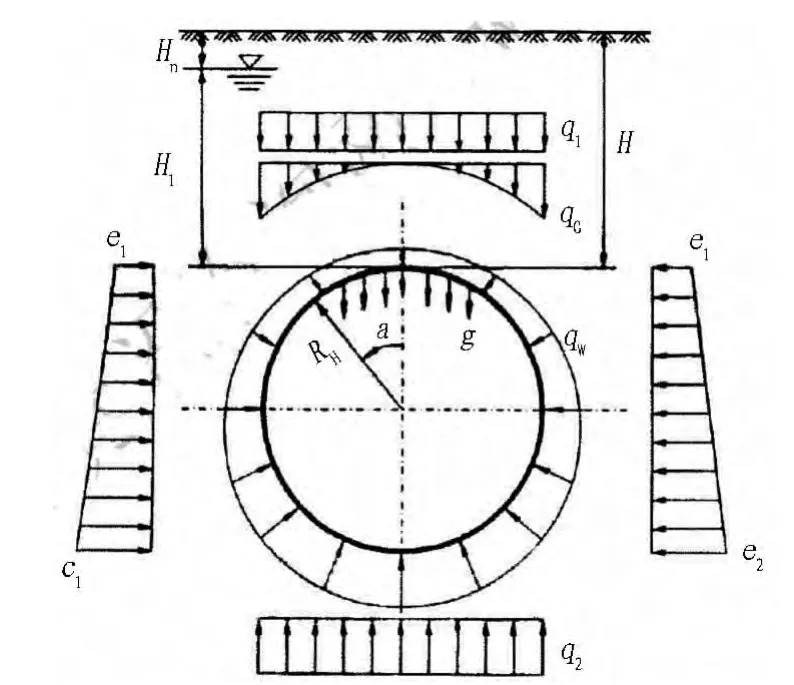
图1 常规盾构隧道荷载模式图Fig.1 External loads of normal shield-bored tunnel
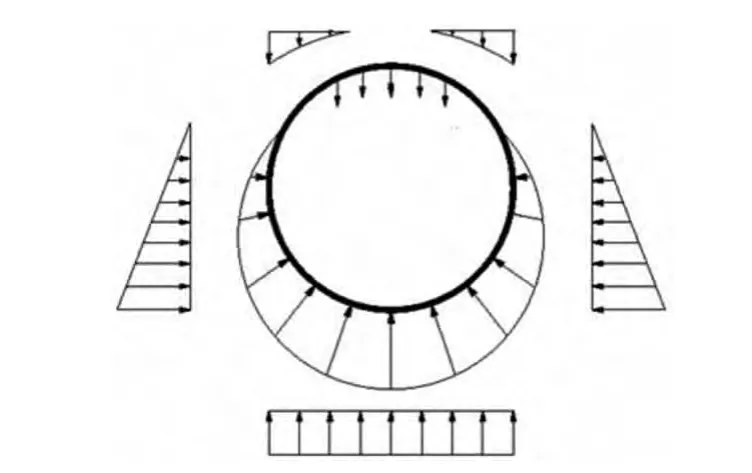
图2 负覆土盾构隧道荷载模式图Fig.2 External loads of shield-bored tunnel without overburden
当隧道处于超浅、负覆土时,与常规隧道情况不同,隧道变形可能呈现竖鸭蛋形,从而影响到水平抗力的大小与分布。本文在建立有限元模型时,采用单向受压土弹簧模拟土体抗力,使水平抗力分布与隧道衬砌变形相协调。
2 地面出入式盾构隧道壳-弹簧模型内力分析
本文依托工程的盾构隧道直径为6.2 m,在超浅覆土工况下,衬砌轴力小于700 kN,弯矩在-150~150 kN·m。应用壳-弹簧模型对盾构隧道内力进行分析时,为更贴近实际情况,模型中接头抗弯刚度考虑其与接头处轴力、弯矩间的非线性关系。接头刚度的取值规律可通过有限元计算。
2.1 盾构隧道接头抗弯刚度有限元计算
基于有限元软件ABAQUS,建立考虑接头尺寸、螺栓孔和密封垫等因素的三维精细化模型[7],如图3和图4所示。有限元模型中,密封垫为超弹性材料,采用Mooney-Rivlin模型模拟,其余材料均为各向同性弹性材料。管片接头处混凝土接触部分设置接触面,切向摩擦因数取0.8,压缩系数取无穷大。对管片接头有限元模型施加不同的水平和竖向荷载,计算盾构隧道衬砌接头位置在不同轴力下弯矩与接头抗弯刚度,如图5所示。

图3 管片接头有限元模型Fig.3 FE model of segment joint

图4 管片接头有限元模型加载示意(单位:mm)Fig.4 Loading of segment joint(mm)
2.2 接头刚度非线性的壳-弹簧模型
2.2.1 壳-弹簧模型计算方法
计算地面出入式盾构隧道外径6.2 m,内径5.5 m,衬砌厚度为350 mm,衬砌由3个标准块、2个邻接块和1个封顶块构成,采用错缝拼装。隧道衬砌采用壳单元模拟,衬砌弹性模量E=34.5 GPa,泊松比μ= 0.2,纵缝及环缝接头均采用弹簧单元模拟。管片纵缝接头弹簧单元的作用包括:轴向压缩拉伸、剪切错动和转动效应等。管片环缝接头弹簧单元的作用包括:沿管片体的环向剪切、沿管片体的径向剪切和沿隧道轴向的压缩及拉伸。本文主要考虑纵缝接头转动刚度Kθz与轴力和弯矩的非线性关系对衬砌内力计算的影响,Kθz由有限元模型计算确定。各剪切刚度主要体现为接头螺栓的抗剪切及混凝土接触面间的摩擦力,由于螺栓与螺栓孔间存在空隙,接触面间存在摩擦等因素,接头的剪切刚度较难确定,计算时可将剪切刚度值取无穷大。建立计算模型接头细部如图6所示。
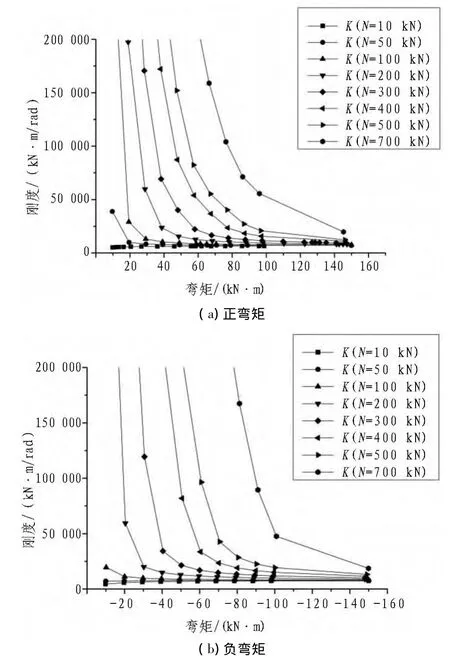
图5 接头刚度与轴力弯矩关系图Fig.5 Relationship between joint rotation stiffness and internal forces

图6 壳-弹簧模型示意图Fig.6 Shell-spring model
计算过程中对接头刚度Kθz进行迭代,通过计算得到接头部位轴力和弯矩确定接头抗弯刚度,当前后2次计算衬砌环变形量小于5%后停止计算。具体计算流程如图7所示。
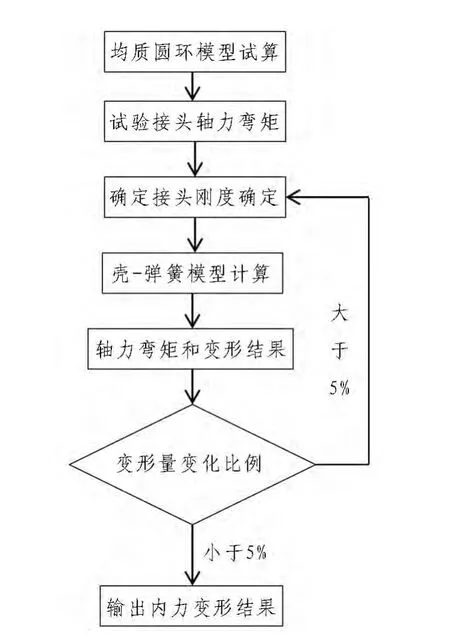
图7 壳-弹簧模型计算流程图Fig.7 Calculation process of shell-spring model
2.2.2 壳-弹簧模型计算与整环管片试验对比
盾构隧道壳-弹簧模型应充分考虑管片间接头的影响,这样较为符合管片的实际受力情况。为验证壳-弹簧模型分析方法的有效性,将其与管片整环加载试验进行对比,管片整环加载试验装置如图8所示。整环试验中管片外径6.2 m,厚0.35 m,管片接头形式与文中所述接头形式一致。
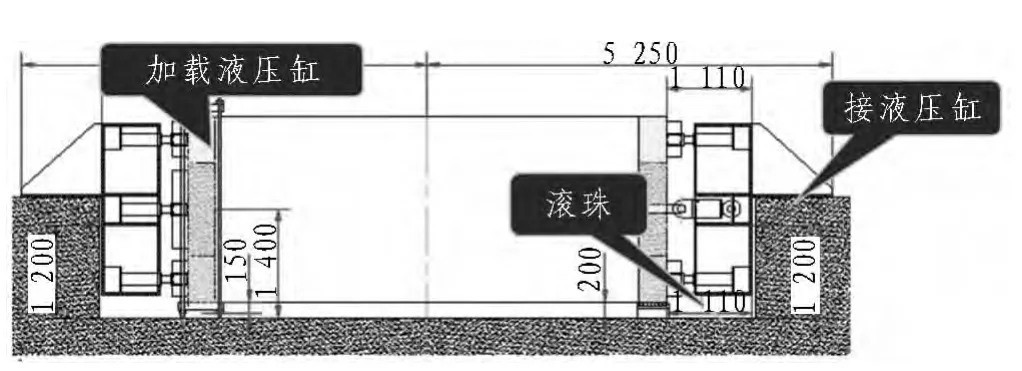
图8 加载装置剖视图(单位:mm)Fig.8 Profile of loading device(mm)
根据文中给出的管片接头抗弯刚度与接头处轴力弯矩值的关系曲线,选用壳-弹簧模型由接头处轴力及弯矩值迭代确定各个接头抗弯刚度的大小,计算隧道埋深0.3D时的变形及内力,如图9—11所示。由图9—11可看出,采用壳-弹簧模型确定各个接头不同的抗弯刚度,可以有效地模拟接头处变形的不连续性,得到的管片变形及内力与试验结果较为接近。
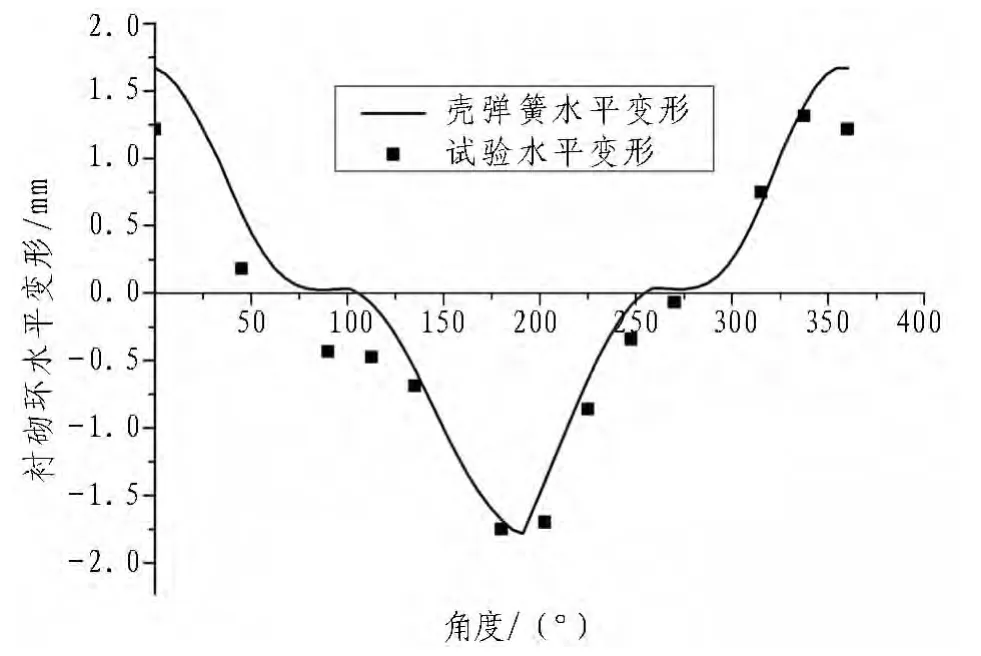
图9 埋深0.3D工况水平变形对比图Fig.9 Horizontal displacement under 0.3D overburden
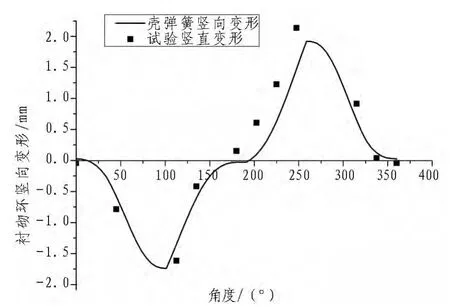
图10 埋深0.3D工况竖直变形对比图Fig.10 Vertical displacement under 0.3D overburden

图11 埋深0.3D工况弯矩对比图Fig.11 Bending moment under 0.3D overburden
3 地面出入式盾构隧道修正惯用法计算参数分析
3.1 分析方法
在采用修正惯用法计算盾构隧道衬砌内力时,首先将衬砌按均质圆环进行计算,考虑纵缝的存在导致抗弯刚度降低,取圆环抗弯刚度为ηEI。计算得到衬砌轴力弯矩后,对接头处弯矩进行重新分配。调整公式如下:

其中:M为均质圆环法计算衬砌接头位置弯矩值;Mj为修正后的接头弯矩;Ms为修正后的管片弯矩。
在采用修正惯用法分析盾构隧道内力时,刚度折减系数η及弯矩传递系数ξ的取值对衬砌内力及变形的结果影响较大。设盾构隧道直径为 D,对埋深-0.3D、零覆土、0.1D、0.3D及0.5D工况,地面出入式盾构隧道修正惯用法计算参数进行分析。根据地面出入式盾构隧道工程现场施工情况,对-0.3D与零覆土工况不考虑地面超载;当埋深为0.1D、0.3D和0.5D工况时,考虑地面有20 kPa超载。侧向土压力采用主动土压力计算,地下水位于地面以下2.5 m,土体参数取值如表1所示。

表1 土体参数表Table 1 Soil parameters
采用ANSYS优化模块,调节均质圆环模型中衬砌刚度折减系数η,使折减后均质圆环模型计算的水平收敛变形、竖直收敛变形和壳 -弹簧模型计算的结果最为接近。2种方法计算衬砌变形情况如图12所示。

图12 衬砌变形示意图Fig.12 Displacement of tunnel segment
按均质圆环模型计算水平径环收敛变形

竖向收敛变形
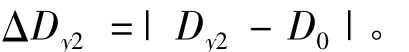
按壳-弹簧模型计算衬砌水平环收敛变形

竖向收敛变形

其中:D0为盾构隧道初始直径;Dx2为按均质圆环模型计算得到的衬砌环变形后水平向直径,Dy2为衬砌环变形后竖向直径;Dx1为壳 -弹簧模型计算得到的衬砌环变形后水平向直径,Dy1为衬砌环变形后竖向直径。
均质圆环模型计算水平及竖向变形的相对误差
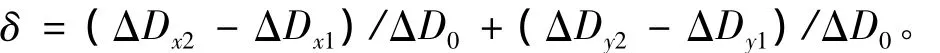
最终取使δ取得最小值的刚度折减系数为最终拟合结果。
确定地面出入式盾构隧道修正惯用法的刚度折减系数η后,分别采用壳-弹簧模型和刚度折减后的均值圆环模型计算衬砌环内力,对比分析均质圆环法计算的衬砌接头位置弯矩和壳 -弹簧法计算的接头位置弯矩,计算得到接头位置的弯矩调整系数
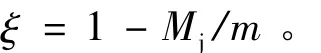
式中:M为均质圆环法计算衬砌接头位置弯矩值;Mj为修正后的接头弯矩。
3.2 刚度折减系数η分析
采用壳-弹簧模型对地面出入式盾构隧道的衬砌变形进行计算,计算结果如表2所示。其中:负值表示隧道变形向内收缩,正值表示隧道变形向外扩张。
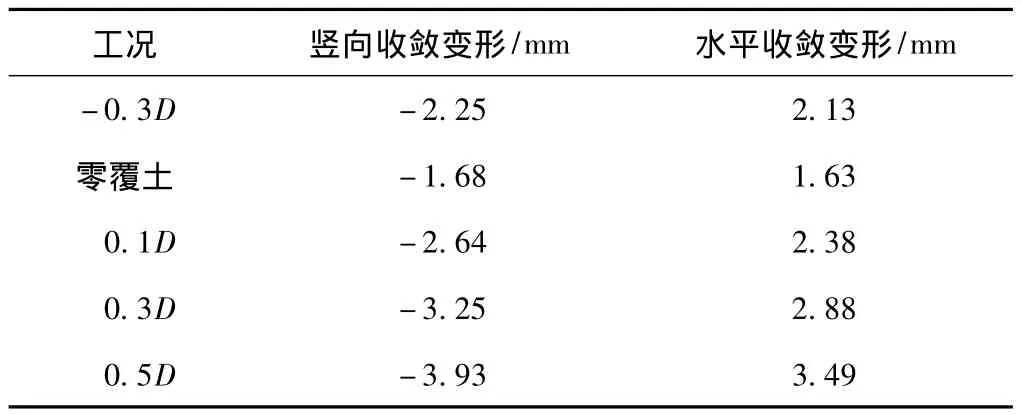
表2 壳-弹簧模型计算衬砌变形Table 2 Segment displacements calculated by shell-spring model
分析刚度折减系数η精度为0.05,取水平变形及竖向变形误差百分比最小的刚度折减系数作为拟合结果。以埋深-0.3D工况为例,采用同刚度折减系数计算得到的水平及竖向变形的相对误差如表3所示。

表3 埋深0.3D工况刚度折减系数拟合结果Table 3 Fitting results of stiffness reduction ratio under 0.3D overburden
采用相同方法对其他各工况的刚度折减系数进行拟合,如表4所示。
几种工况计算的的变形误差均较小,一般在5%以下,只有埋深0.1D工况误差(5.8%)略大。得到的刚度折减系数值比较接近,取值基本在规范范围内,但是取值相对较小。
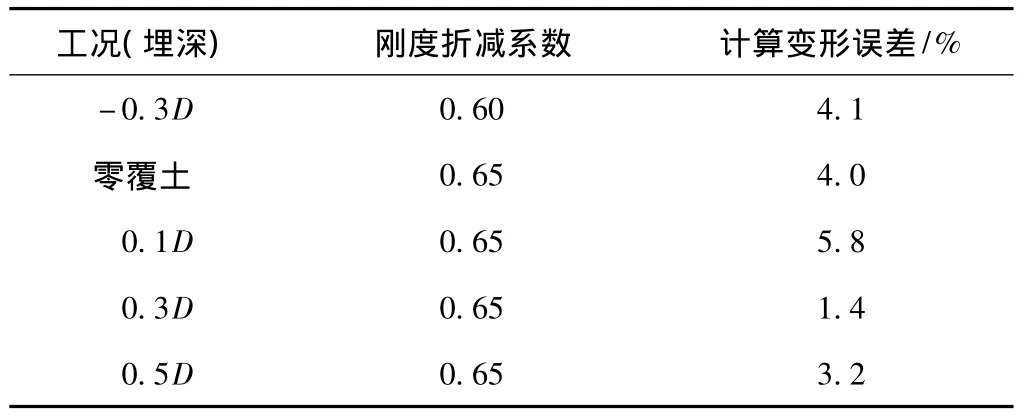
表4 刚度折减系数η分析结果Table 4 Analysis results of stiffness reduction ratio η
3.3 弯矩调整系数ξ分析
接头弯矩调整系数与接头位置的接头刚度和变形情况直接相关,而不同位置接头的轴力弯矩一般不同,接头刚度不同,所以即使环相同,不同位置的接头弯矩调整系数也会存在较大差异。隧道错缝拼装时采用不同的拼装角度,接头弯矩调整系数也会受到较大影响。本文根据实际工程设计对弯矩传递系数进行分析,相邻两环采用45°错缝拼装,两环分别顺时针转动22.5°和逆时针转动22.5°。接头位置和编号如图13所示。
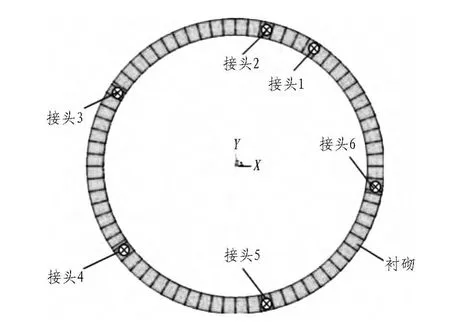
图13 隧道接头位置及编号示意图Fig.13 Number and position of segment joint
根据匀质圆环及壳-弹簧模型接头处弯矩计算结果,得到各工况地面出入式盾构隧道接头弯矩调整系数如表5所示。露出地面的工况,即埋深-0.3D及零覆土工况,由于接头刚度较小,弯矩传递系数很大,且不同接头的刚度差距较大。因此,不同接头的弯矩传递系数相差较大,接头1的弯矩传递系数达到90%以上,个别接头弯矩调整系数明显大于规范推荐值,采用规范值计算衬砌内力则不安全。地面以下有覆土的工况,接头刚度都比较大,且各接头刚度相差不大,弯矩传递系数最大值在0.5左右。

表5 不同工况不同位置接头弯矩调整系数表Table 5 Joint moment release ratio at different positions and situations
4 结论与讨论
本文基于壳-弹簧模型,考虑接头抗弯刚度与接头轴力弯矩的非线性关系,对地面出入式超浅埋盾构隧道修正惯用法的关键计算参数η和ξ的取值进行分析研究,最终得到以下结论。
1)地面出入式盾构隧道在浅埋段衬砌抗弯刚度折减系数η较小,建议采用规范规定的最小值进行变形计算。
2)地面出入式盾构隧道弯矩调整系数ξ值较大,超浅埋地下段宜取规范规定的较大值,负覆土段隧道弯矩调整系数ξ偏保守,可取1进行计算。
3)地面出入式盾构隧道负覆土段,宜采用接头刚度非线性的壳-弹簧或者梁-弹簧模型进行分析。
另外,对于管片接头刚度与内力的非线性关系,本文在试验方面的研究尚不深入,将来需结合更多的管片整环试验进行深入研究。
[1] 张凤详,朱合华,傅德明.盾构隧道[M].北京:人民交通出版社,2004.(ZHANG Fengxiang,ZHU Hehua,FU Deming.Shield Tunnelling Method[M].Beijing:China Communications Press,2004.(in Chinese))
[2] 上海现代建筑设计(集团)有限公司.DGJ 08—11—2010地基基础设计规范[S].上海:市建筑建材业市场管理总站,2010.
[3] 吴惠明,周文波,滕丽.地面出入式盾构法隧道新技术[J].隧道建设,2014,34(1):67-72.(WU Huiming,ZHOU Wenbo,TENG Li.Case study on ground penetrating shield technology(GPST)[J].Tunnel Construction,2014,34(1):67-72.(in Chinese))
[4] Oriole Arnaud.Climent Molins.Three dimensional structural response ofsegmentaltunnellinings[J].Engineering Structures,2012,44:210-221.
[5] 朱伟,黄正荣,梁精华.盾构衬砌管片的壳–弹簧设计模型研究[J].岩土工程学报,2006,28(8):940-947.(ZHU Wei,HUANG Zhengrong,LIANG Jinghua.Studies on shell-spring design model for segment of shield tunnels[J].Chinese Journal of Geotechnical Engineering,2006,28(8): 940-947.(in Chinese))
[6] 苏宗贤,何川.盾构隧道管片衬砌内力分析的壳-弹簧-接触模型及其应用[J].工程力学,2007,24(10):131-136.(SU Zongxian,HE Chuan.Shell-spring-contact model for shield tunnel segmental lining analysis and its application[J].Engineering Mechanics,2007,24(10):131-136.(in Chinese))
[7] 庄茁,由小川,廖剑晖,等.基于ABAQUS的有限元分析和应用[M].北京:清华大学出版社,2009.

