基于启发式分割和近似熵法的径流序列变异诊断*

黄生志，黄 强，王义民，陈昱潼

(西安理工大学西北旱区生态水利工程国家重点实验室培育基地，陕西 西安 710048)

随着全球气候的变化以及日益加剧的人类活动的影响，流域水文要素以及水文情势诸如河川径流、湖泊蓄水以及流域降雨等无论是在时间上还是空间上均有可能发生变异，致使水文资料的一致性遭到破坏[1-2]。水文资料一致性的破坏将会给水文分析、水文模拟、水文计算以及流域的水资源规划等带来巨大的影响[3-5]，进而导致变异前的成果不能再继续使用，否则将产生极大的偏差。对流域水文变异进行诊断，不仅有助于掌握流域水文要素的演变规律，还能避免因使用一致性被破坏的水文资料进行设计或分析而产生重大失误或者损失。

基于此，国内外不少学者对水文变异进行了研究并取得了大量的研究成果。诸如Lee等[6]运用了贝叶斯推断理论对水文变点进行了研究。然而，该方法对资料的要求过高且对样本分布的假设过多，因此在实际的应用过程中操作性不强[7]；陈广才等[8]针对潮白河水资源分区的45 a年径流量序列，采用基于平稳与线性的检验假定的滑动F检验法、滑动T检验法以及秩和检验法等统计的方法，进行了径流序列的变异诊断。事实上，水文序列受到气候变化以及人类活动的影响，往往呈现出高度的非线性和非平稳性，使用传统的统计诊断方法对水文序列的变异点进行检验则往往产生一定的偏差[9]。

由Bernaola-Galván[10]提出的启发式分割法主要用于处理非线性及非平稳时间序列的均值变异点。同传统的变异检验方法相比，启发式分割法能够将一个非平稳的时间序列分割成多个平稳的子序列，各子序列的均值互不相同并表征不同的物理背景，能较好地弥补传统检验方法的不足。由于该方法在分割时采取了一分为二的迭代算法，因此，极大地减少了计算量，具有较好的实用性[9]。此外，由Pincus于20世纪90年代提出的近似熵(approximate entropy)，因其具有较好的抗干扰与处理非稳态序列能力且所需数据量较少等优点，故在机械设备故障的诊断及医学等领域得到广泛地应用[11]。鉴于此，本文基于启发式分割算法与近似熵理论，对渭河流域的年径流量进行变异诊断，并对其变异进行归因分析。

1 研究区域与数据

1.1 研究区域概况

渭河作为黄河流域最大的一级支流，发源于甘肃省内渭源县的乌鼠山，自西向东分别流经甘肃的陇西、天水，陕西的宝鸡、西安、渭南，最终于潼关汇入黄河[12]。渭河的干流全长约为818 km, 总流域面积约为13.5万km2(图1)。渭河流域位于34°-38°N，104°-110°E，属于大陆性季风气候，春季温暖少雨，夏季雨热同期且有伏旱，秋季凉爽湿润，冬季寒冷少雨。流域的最冷月平均气温大约是-3～-1℃，最热月平均气温大约为23～26℃[12]。流域降雨空间分布不均，由东南向西北递减，秦岭南麓雨水充沛，最大年降水量超过1 000 mm，而平原河套地区年降水量仅为500 mm左右[12]。

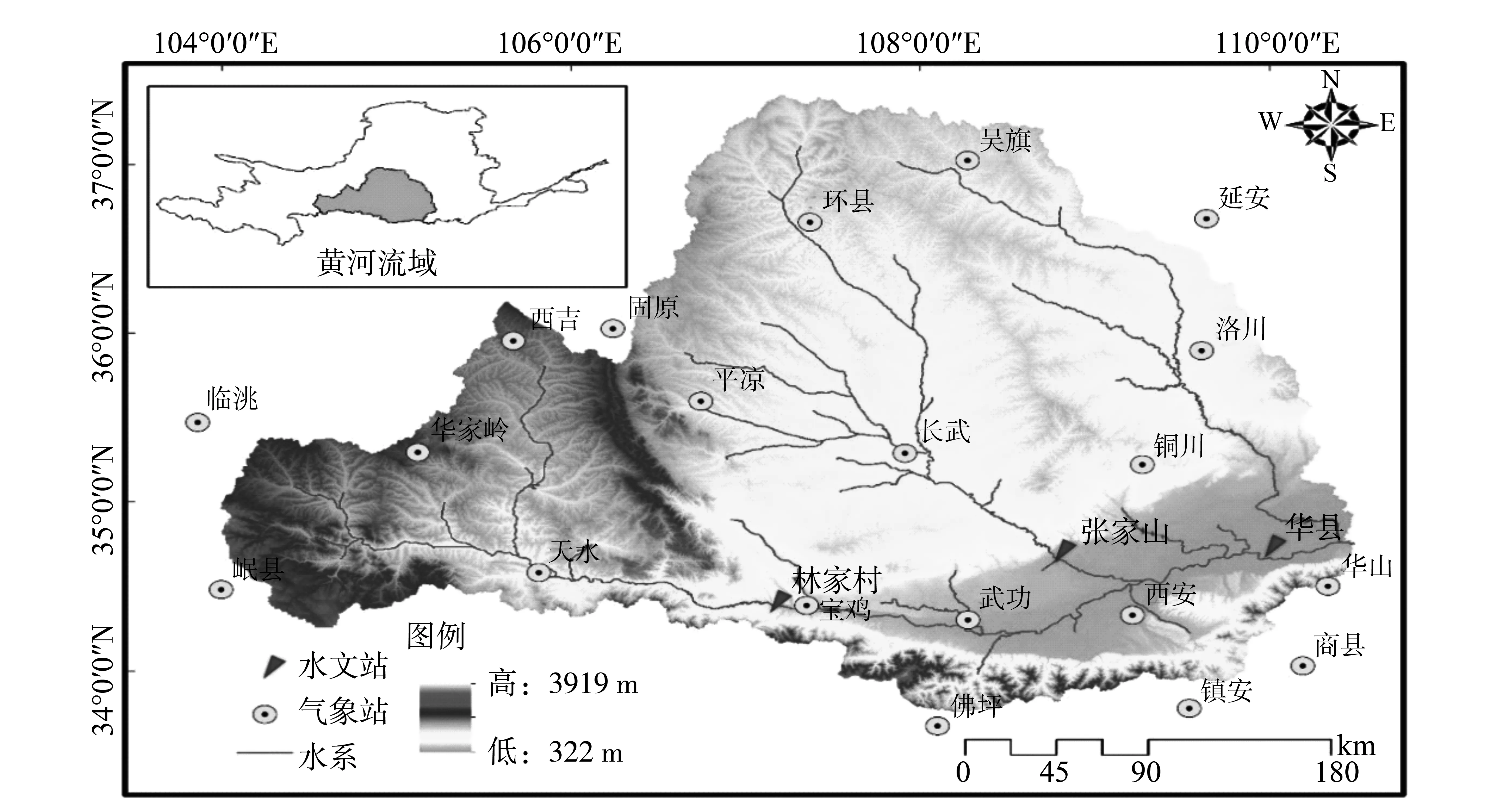
图1 渭河流域及相关水文站位置Fig.1 The location of the Wei River Basin and the related hydrological stations

流域降水年内分配不均且年际变化大，汛期降水量约为年降水量的65%。自从国家实行西部大开发这一国策以及成立了关中-天水国家级经济开发区后，渭河流域的经济社会高速发展，工业用水、农业用水量剧增。因此，人类大量开采与利用地下水及地表水，致使渭河流域的河川径流显著减少。此外受全球气候变化的影响，近年来渭河流域的降雨呈现下降的趋势，如此一来渭河流域水文情势将发生巨大的变化，日益减少的水资源将难以满足渭河流域经济社会的可持续发展。鉴于渭河流域用水安全的重要性，为了进一步掌握渭河流域河川径流的演变规律，本文对该流域的年径流量进行变异诊断，并对变异结果进行归因分析。本文将研究区域划分为三个部分，分别为林家村水文站以上流域，该区域代表渭河流域的中上游；张家山水文站以上流域，该区域代表渭河最大的支流泾河流域；华县水文站以上流域，该区域代表整个渭河流域。

1.2 数据

本研究所用数据为渭河流域21个气象站的1960-2005年的日气象数据，通过求和运算得到各个气象站的降雨、气温、风速、日照变化率等年气象序列以及林家村、张家山以及华县水文站的1960-2005年的日径流序列，通过求和而得到各水文站的年径流量，渭河流域及各站点所在的位置如图1所示。以上气象数据均来源于中国国家气象中心，水文数据摘自水文手册。所有数据在使用之前均进行了三性审查，审查结果表明本文所采用的水文气象数据具有较好的可靠性、一致性以及代表性，可以用作相应分析。潜在蒸发量是通过Penman-Monteith 公式计算而成。

2 研究方法

2.1 启发式分割算法

某一时间序列x(t)由N个点组成，其中一个分割点i从序列的左边沿着该序列依次向右边滑动，分割点左边和右边部分的平均值分别为μ1(i)和μ2(i)，其标准差分别是s1(i)和s2(i)，i点的合并偏差SD(i)可表示为[9,13-14]：

(1)

式中，N1、N2分别表示i点左边与右边部分的点数。其中，i点左右两边两子序列均值的差异能够使用t检验统计值T(i)来进行度量[9]：

(2)

T值越大，则说明该点左右两边两子序列的差异越明显。计算T(t)中最大值Tmax所对应的统计显著性P(Tmax)，其计算公式如下[9]：

(3)

通过蒙特卡洛模拟可得：η=4.19lnN-11.54且δ=0.40。其中，N表示该序列的长度，v=N-2,Ix(a,b) 是不完全β函数。预先设定一个临界值P0，当P(Tmax)≥P0，则在该点处将此序列分割成左右两个均值差异较大的子序列，否则不进行分割[9]。对得到的新序列不断进行迭代并重复以上操作，直到子序列的长度小于0(0是最小分割尺度)时便停止对其分割。由此，便将原序列分割成几个均值不同的子序列，而分割点则为该序列的均值变异点。

通常情况下，P0取值范围为0.5～0.95，而0的取值则不应小于25[15]。通过不断调整的大小，能够实现对该时间序列不同尺度上的变异检测[9]。

2.2 近似熵方法

近似熵方法实质上是一种基于边缘概率分布统计的定量描述某一时间序列的复杂程度的方法，该算法的具体步骤简要介绍如下[11]。

假定某一长度为N的时间序列u(1),u(2), …,u(N)，在该时间序列中构造一组m维数的向量X(1),X(2), …,X(N+m-1),其中向量为[11]：

X(i)={u(i),u(i+1),…,u(i+m-1)}

i=1,2,...,N-m+1

(4)

定义两个向量X(i)与X(j)之间的距离d[X(i),X(j)]是两个向量中对应的元素的最大值[11]：

d[X(i),X(j)]=max[|u(i+k)-u(j+k)|]

k=0,1,...,m-1

(5)

对于每一个i，定义两个向量X(i)与X(j)之间的关联程度：

(j)]≤r的个数}/

(N-m+1)

(6)

(7)

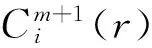
(8)

然而，实际上N不可能为无穷大。当N取有限值时，便可得到近似熵的估计值，表示为：

ApEn(m,r)=φm(r)-φm+1(r)

(9)

3 结果与讨论

3.1 基于启发式分割算法的年径流变异结果分析

根据上述2.1的具体步骤，将P0设定为0.95，0的取值则设为25，分别得到林家村以上流域、张家山以上流域以及整个渭河流域的年径流变异分析结果，如图2所示。

由图2(a)中的第一次分割可知，1971年对应的T值最大，并且其相应的P(Tmax)等于1要大于临界值0.95。因此，1971年是林家村以上流域年径流序列的第一个突变点；从第二次分割可知，1994年所对应的T值最大，且其相应的P(Tmax)等于0.998 5，也大于临界值0.95，故1994年为该流域年径流序列的第二个突变点。

由图2(b)可得，张家山以上流域的年径流序列并无突变点，因其最大T值的P(Tmax)小于0.95。对于整个渭河流域的年径流序列，由图2(c)中第一次分割可知，1969年的T值为最大值，其对应的P(Tmax)等于0.992 9，大于临界值0.95，因此1969年为第一个变异点；由其第二次分割可得，1993年的T值为最大值，其对应的P(Tmax)等于0.971 8，大于临界值0.95，故1993年为第2个变异。

3.2 基于近似熵的年径流变异分析结果

根据上述2.2求近似熵的具体步骤，采用滑动窗口的方法，将窗口宽度设为5，滑动步长设为1，m和r分别设为2和0.15σ。其中，σ为原始序列的标准差，分别得到林家村以上流域、张家山以上流域以及整个渭河流域的基于近似熵的年径流变异分析结果于图3(a)-(c)中。

这时零售商的和供应商的期望收益均是供应链整体期望收益函数的仿射函数，同时各企业的最优定货量q*相同，这表明在无突发事件下基准契约能实现供应链协调.

由图3(a)可知，林家村以上流域年径流1960-1971年间的近似熵较大，而1971-1994年间的近似熵较小，1971年明显是一个变异点，而1994-2005年间的近似熵较大，易知1994年为另一变异点。由图3(b)可知，张家山以上流域年径流序列的近似熵没有显著的变异情况。因此，该流域的年径流序列无变异点。而由图3(c)中整个渭河流域年径流的近似熵明显可知，渭河流域年径流序列明显存在两个变异点，分别为1969与1993年。该结果与基于启发式分割算法的结果一致，进一步论证了以上3个流域年径流序列变异点的正确性，也充分展示了基于启发式分割算法及近似熵理论在水文变异诊断上的优越性。

3.3 流域年径流变异点的印证

3.3.1 累积年径流与年份关系图 虽然通过启发式分割算法及近似熵方法已经发现林家村以上流域年径流序列存在2个变异点(1971和1994年)，张家山以上流域年径流序列无变异点存在，整个渭河流域年径流序列也存在两个变异点(1969和1993年)。

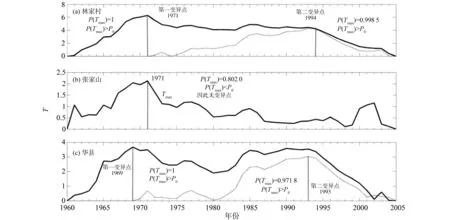
图2 年径流启发式分割检验图Fig.2 The test chart of annual runoff based on heuristic segmentation algorithm

为了进一步证明这两个算法的在变异诊断上的准确性，绘制3个流域的累积年径流量与年份的关系图，其结果如图4所示。

由图4实心圆部分可以明显看出林家村以上流域累积年径流被2个变异点分成了3部分，且每部分的线性拟合度都很高。其中，1960-1971与1972-1994年2个部分的线性拟合相关系数高达0.99，而1995-2005的线性拟合系数为0.96。而这两个变异点恰好与上述3.2节中基于启发式分割法及近似熵理论所找到的关于林家村以上流域年径流序列的变异点相一致。图4空心五角星部分所表示的是张家山以上流域累积年径流量与年份之间的关系，在整个研究阶段1960-2005年间，所有的点均拟合于一条直线，且拟合精度高，其相关系数高达0.99。因此，在1960-2005年间，张家山以上流域年径流序列无明显变异点存在。由图4的空心圆部分可知，整个渭河流域的累积年径流量被1969与1993年这2个变异点分成了3个部分，每个部分点的线性拟合程度都很高，3个部分的相关系数均高达0.99。因此，通过累积年径流量与年份的关系图可知，整个渭河流域的年径流序列存在1969和1993年这2个变异点，而这又与上述利用启发式分割法及近似熵理论所发现的整个渭河流域年径流量的变异的十分吻合。由此进一步论证了基于启发式分割法及近似熵理论在水文变异诊断中的准确性；与此同时，进一步印证了渭河流域年径流序列存在变异的事实。其中，林家村以上流域与整个渭河流域的年径流序列的确存在两个变异点，而张家山以上流域年径流序列并无变异点存在。此外，对于林家村以上流域和整个渭河流域被两个变异点分割成的3个部分而言，其拟合直线的倾斜度均随着时间推移而不断减小，由此可知这两个流域的径流量有着明显的下降趋势，而实际上也确实如此。该研究结果与拜有存[16]的基于差异信息理论的渭河径流序列变异诊断结果基本一致，他发现渭河流域的年径流存在这两个变异点。

3.3.2 变异前后各参数对比 分别计算存在变异点的林家村以上流域以及整个渭河流域变异前后径流序列的均值、方差以及变差系数等参数，进一步对比分析变异点前后序列的差异性，具体的参数值如表1所示。由表1可知：① 林家村以上流域由两个变异点所分割成的3部分径流序列无论是均值还是方差均有较大差别，就均值而言，1972-1994年间的年径流均值较1960-1971年减少了42.2%，而年径流均值1995-2005年比1960-1972年减少了77.3%，可以说3个部分的均值差别比较明显。② 而就方差而言，1972-1994年间的年径流序列的方差较1960-1971年减少了71.4%，而1995-2005年的年径流序列的方差同1960-1972年相比减少了86.9%，由此可知，这3部分的方差差异性较大。但是，对于变差系数而言，1972-1994年间的变差系数值较1960-1972年变化不大，而1995-2005的年径流序列的变差系数与1960-1972年相比减少了40.9%。③ 整个渭河流域的年径流序列变异前后参数的变化规律与林家村以上流域类似，3个部分的均值与方差的差异性较大，1970-1994年间的变差系数值同1960-1970相比变化不大，而1994-2005的年径流序列的变差系数较1960-1969年减少了25%。

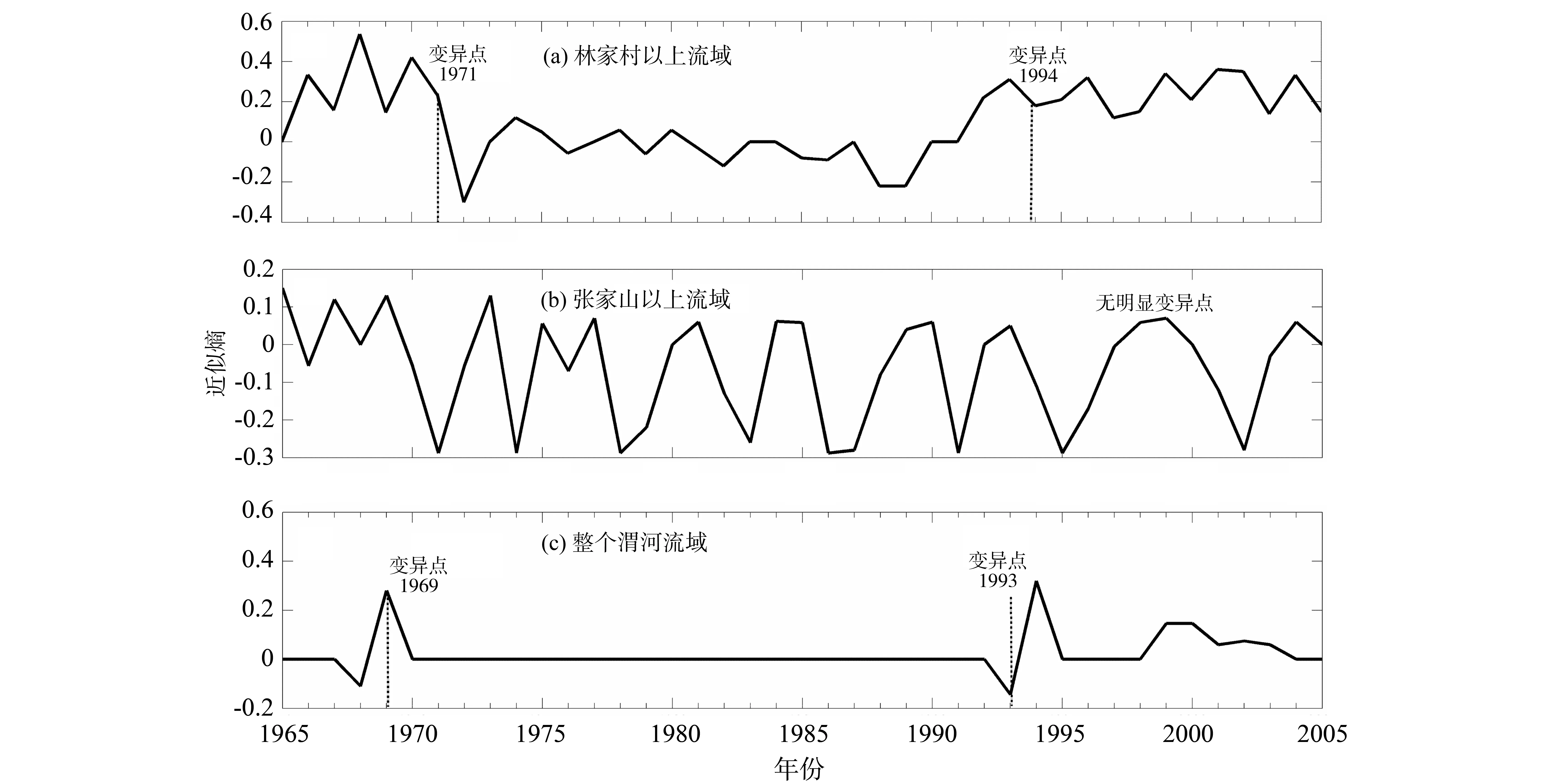
图3 年径流的近似熵检验图Fig.3 The test chart of annual runoff based on approximate entropy method

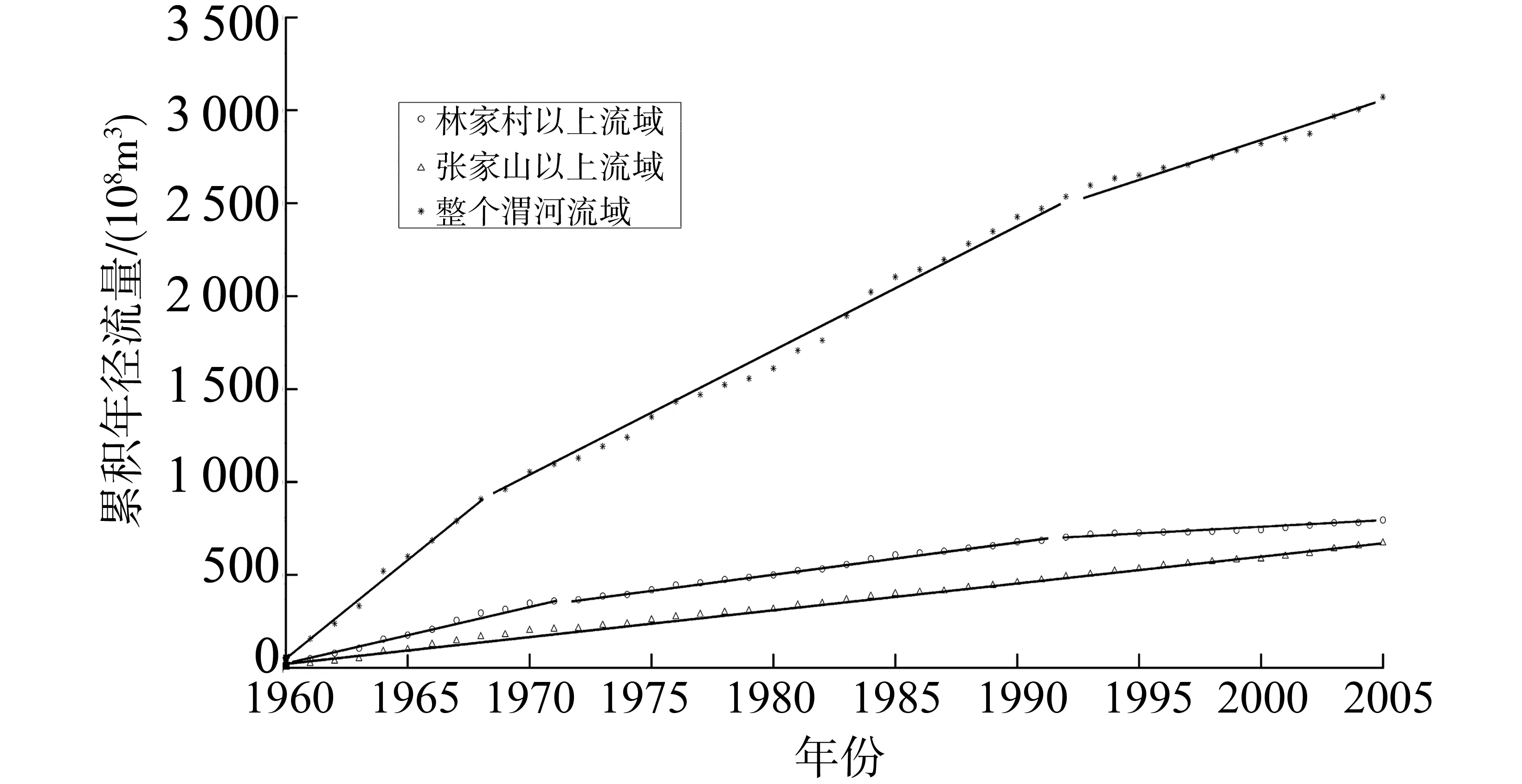
图4 三个流域累积年径流量与年份的关系图Fig.4 The relationship between accumulative runoff and year in the three basin

总的来说，被两变异点分割成的3个年径流序列在均值与方差上差异明显，并且均值、方差及变差系数有明显的减小趋势。由此可侧面证明变异点的正确性。

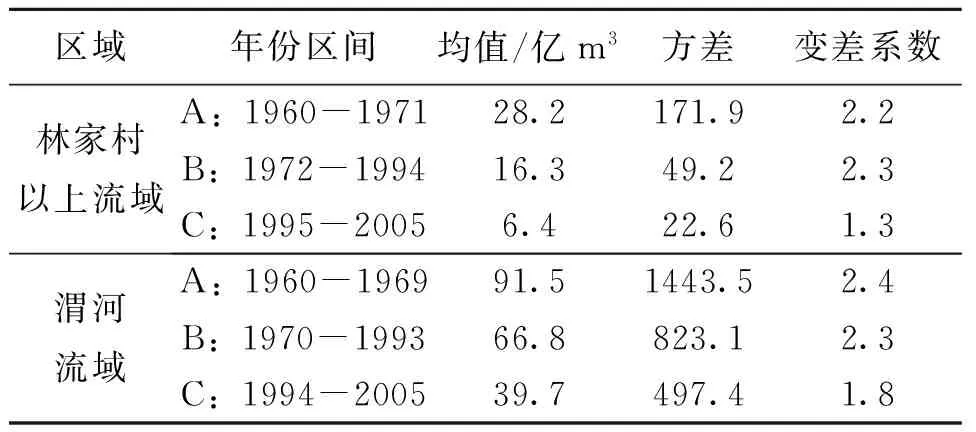
表1 两流域年径流序列变异前后参数对比表Table 1 The comparison of parameters of the annual runoff before and after the change points in the two basin

3.4 径流变异的归因分析

3.4.1 气候变化的影响 采用Mann-Kendall法求算变点前后降雨和潜在蒸发的变化趋势，其结果如表2所示。

由表2可知，林家村以上流域与渭河流域的降雨和潜在蒸发变点前后的变化趋势相似。降雨先减小后变大，但在整个时间序列表现为不显著地下降趋势。潜在蒸发量先增大后减小再增大，在整个时间序列表现为不显著的上升趋势。从常规分析上可知渭河流域与径流联系密切的降雨与潜在蒸发等气象因子均未发生显著变化，人类活动对径流变异的影响或许更强。然而，渭河流域地处中国大陆性季风区，受西太平洋副热带高压系统的影响。1971年时，西太平洋副热带高压系统有所减弱并发生一个El Nio事件致使中国大部分地区的大气环流及气候发生变异，从而导致渭河流域当年降雨量剧减[17]，而此时恰好是林家村以上流域年径流序列的第一个变异点所对应的时间。而1994年时，另外一个ENSO事件发生，此时西太平洋副热带高压系统异常强大，导致渭河流域当年的降雨量较年平均降雨量减少了14.9%[18]，而此时恰好对应于林家村以上流域及整个渭河流域年径流序列的第2个变异点。

3.4.2 人类活动的影响 20世纪70年代初，渭河流域修建了不少水利工程，如1970年修建的羊毛湾水库和冯村水库，1972年修建的大峪水库和石门水库。这些水库的修建，极大地改变河川径流的时空分布规律，破坏天然的径流规律，从而导致径流序列变异。除了兴建水利工程外，流域下垫面的变化也改变河川径流的演变规律。50年代末60年代初，由于经济困难与政治运动的缘故，大量的树木遭到破坏，尤其在1958年的“大炼钢铁”时期，集中砍伐了大量的林木，从而造成了严重的水土流失，由此也使得1960-1970年间的径流量较大[19]。但是，随着水土保持措施的开展，尤其是70-80年代，渭河流域对水土流失开展了一系列有组织、有计划、有步骤的防治工作，并取得了很好的成效，从而在一定程度上减小了渭河流域的水土流失量。因此，在1973-1994年间河川径流较1960-1970年有一定的减少。此外，随着人口的迅速增加以及经济的高速发展，渭河流域的工业用水和农业用水增长迅速。其中，1990-2000年间，国民经济各行业用水增加了17.1亿m3，年均增长率为3.2%，远高于全国平均1.1%和黄淮海流域的0.3%。90年代后的渭河流域国民经济平均用水量为42.62亿m3，比90年代前增加了52.6%。大量地开采与开发地表水和地下水，是渭河流域径流序列变异的又一重要因素。

表2 变点前后降雨和潜在蒸发的变化趋势Table 2 The trend of precipitation and potential evaporation before and after change points

4 结 论

为了探究渭河流域河川径流变异情况，本文采用1960-2005年林家村、张家山以及华县3个水文站的日径流数据，将研究区域划分为林家村以上流域、张家山以上流域以及整个渭河流域3个部分。基于启发式分割算法与近似熵方法对各流域的年径流序列进行了变异诊断，并利用累积年径流量与年份的关系图对变异结果进行判定分析，得到主要结论如下：

1)启发式分割算法与近似熵方法均具有较好的检验均值突变点的能力，具有较强的抗噪抗干扰的能力，十分适应于非线性非稳态的径流序列的变异诊断，能够准确地找到其变异点。

2)林家村以上流域存在2个变异点，分别是1971和1994年；张家山以上流域无变异点存在；整个渭河流域存在两个变异点，分别是1969和1993年。

3)对于林家村以上流域和整个渭河流域而言，被两个变异点分割成3个子序列的线性趋势线的斜率随着年份的增大而不断减小，由此说明在这两个流域，其径流量有明显的减小趋势。

4)造成渭河流域河川径流变异的主要原因是气候变化与日益增长的人类活动。其中，气候变化主要是1971年的El Nio事件和1994年的ENSO事件的发生致使当时渭河流域降雨量剧减，从而引起径流量的显著减少。人类活动则具体包括水利工程建设、流域下垫面的改变以及由于人口和经济的增长而大量开采与开发地下水和地表水，由此而使得河川径流发生变异。

[1] 邓建伟，宋松柏，卢书超. 石羊河流域年径流序列的变异诊断[J]. 西北农林科技大学学报:自然科学版，2006，34(4) ：121-124.

[2] 李艳，陈晓宏，张鹏飞. 北江流域径流序列年内分配特征及其趋势分析[J]. 中山大学学报:自然科学版， 2007， 46(5) ：113-116.

[3] 丁晶，刘权授. 随机水文学[M]. 北京：中国水利水电出版社，1997.

[4] 王孝礼，胡宝清，夏军. 水文序列趋势与变异点的R/S分析法[J]. 武汉大学学报：工学版，2002，35(2)：10-12.

[5] 詹道江，叶守泽. 工程水文学[M]. 北京：中国水利水电出版社，2000.

[6] AUSTIN F S L, SYLVA M H. A shift of the mean level in a sequence of independent normal random variable-A Bayesian Approach [J]. Technometrics, 1997, 19(4): 503-506.

[7] 肖宜，夏军，申明亮，等. 差异信息理论在水文时间序列变异点诊断中的应用[J]. 中国农村水利水电，2001(11)：28-30.

[8] 陈广才，谢平. 水文变异的滑动F识别与检验方法[J]. 水文，2006，26(2)：57-60.

[9] 陈广才，谢平. 基于启发式分割算法的水文变异分析研究[J]. 中山大学学报:自然科学版，2008，47(5)：122-125.

[10] BERNAOLA-GALVN P, IVANOV P C, AMARAL L A N,et al. Scale invariance in the nonstationarity of human heart rate[J].Physical Review Letters, 2001, 87:168105.

[11] 王启光，张增平. 近似熵检测气候突变的研究[J]. 物理学报，2008，57(3)：1976-1982.

[12] 张宏利，陈豫，任广鑫，等. 近50年来渭河流域降水变化特征分析[ J].干旱地区农业研究，2008，26(4)：236- 241.

[13] 李海彬，张小峰，胡春宏,等. 基于B-G分割算法的河川年输沙量突变分析[J]. 水利学报，2010，41(12)：1387-1391.

[14] 封国林，龚志强，董文杰. 基于启发式分割算法的气候突变检测研究[J]. 物理学报，2005，54(11)：5494-5499.

[15] 龚志强. 基于非线性时间序列分析方法的气候突变检测研究[D]. 扬州：扬州大学，2006.

[16] 拜有存. 基于差异信息理论的渭河年径流变异点诊断[J]. 人民黄河，2009，31(7)：29-30.

[17] BAI H，MU X M，WANG F，et al. Analysis on evolution law of meteorological and hydrological drought and wetting[J]. Agricultural Research in the Arid Areas，2012，30:237-241.

[18] ZHANG H L，CHEN Y， REN G X. The characteristics of precipitation variation of Weihe River Basin in Shaanxi Province during recent 50 years[J]. Agricultural Research in the Arid Areas，2008，26:236-240.

[19] 张淑兰，王彦辉，于澎涛,等.定量区分人类活动和降水量变化对泾河上游径流变化的影响[J]. 水土保持学报，2010，24(4)：53-58.