一种自确认软测量方法的研究与应用*

肖红军，刘乙奇，伍 俊

(1．佛山科学技术学院 机械与电气工程学院, 广东 佛山 528000；2．华南理工大学 自动化科学与工程学院, 广东 广州 510640)

在过程控制中，常规仪表常常会遇到购买及维护费用过高，延迟过大甚至工作条件过于恶劣等问题，因此，软测量技术广泛应用于代替或部分代替仪表的功能以达到系统进行监控的目的[1-3]。软测量是依据可测或易测变量(辅助变量)建立模型对难以直接测量变量(主导变量)进行测量和估计的方法[4]。但是，软测量是通过输入传感器的输入变量和模型进行预测的，如果某一个传感器发生故障，将直接导致软测量预测的偏离甚至失效。因此，在软测量进行模型预测之前，有必要对其输入传感器进行有效的校验。尽管大量学者对传感器的故障诊断和辨识进行了大量研究[5-6]，但是，鲜有学者研究专门针对软测量的输入传感器的故障诊断和辨识，故障重构更是少之又少。Martin和罗中良等提出了经网络对输入传感器进行校验[7-8]，在他们的方法中，如果输入测量数据超过某一限值，操作员则利用经验知识手动的替代故障的数据。可是，这在过程工业中显得不切合实际。通过最小化SPE故障检测的原理，Qin等提出了基于SPE和T2的故障辨识和重构方法[9]。但是，单纯的SPE或T2故障检测方法容易产生误报警。Yue和Qin等[6]混合了SPE和T2指标进行故障检测，并获得了不错的效果。但由于重构算法比较复杂和耗时，在实际中不易实现，同时混合指标的限值不容易确定。

SEVA(自确认)仪表是自带自检测参数的一种新型仪表，由牛津大学和Foxboro提出的标准，并在热电偶和溶解氧传感器中得到了应用[10]。本文在此基础上研究预测模型的综合输出机制，模型的输出将不是单个预测值的输出，而是同时输出五种信息：带概率区间的输出、模型的状态(故障状态，重构状态和迷失状态等等)、不确定性、故障信息和校验输出值，并对发生故障的输入传感器进行数据重构和修复以达到模型自校验和自诊断的目的。特别需要指出的是本文创新性的运用鲁棒统计学中的CP(Confidence Predictor)技术对预测模型的不确定进行定性的描述。此外，可以将输入传感器的状态也作为模型的输出，从而达到对预测模型从输入、模型和输出的三方位检测，使得模型的输出不再只是单纯的预测值，还有不确定区间和输入传感器的输入状态。

1 统计学分析方法

1.1 主元分析(PCA)

PCA根据保留最大数据方差的条件下对输入变量进行降维约简[11]。假设X是n×m的数据矩阵，PCA将多变量的输入数据矩阵进行奇异值分解后得到主元和特征向量：

(1)

其中ti∈Rn被称为得分向量，即矩阵X的主元，pi∈Rm被称为负荷向量，是残差矩阵，它包含了系统的数据的主要噪声。T=[t1,t2,…,tn]和P=[p1,p2,…,pm]分别是得分向量矩阵和负荷向量矩阵。给定一个新的采样向量，PCA的得分向量，预测和残差向量的关系如下：

ti=xpi

(2)

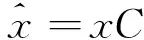
(3)

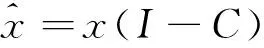
(4)

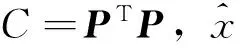
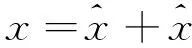
(5)

统计量SPE主要用于测量残差数据的变化

(6)

正常情况下，SPE是可以忽略不计的。但是，如果某一个传感器发生故障SPE将急剧变大，可用于传感器故障的诊断。但是SPE对噪声过度敏感从而极易导致误报警。基于上述分析，本文将通过最小化SPE改进传感器故障诊断指标，并提出SVI指标。在软测量预测之前，SVI可以用来确认软测量的输入数据的正常与否。与此同时，故障的传感器数据能被PCA模型的估计值进行重构。另外，PCA还能用于软测量建模过程中JIT算法的数据选择。

1.2 递归偏最小二乘法(RPLS)

PLS方法将高维数据空间投影到低维特征空间，得到相互正交的特征向量，再建立特征向量间的一元线性回归关系[12]。假定一个输入输出组成的矩阵数组{XY}, 输入输出矩阵可表达为

X=TPT+E

(7)

Y=UQT+F

(8)

其中T∈Rn×d和U∈Rn×d分别是X和Y的得分向量矩阵，d是负载向量的个数。而P∈Rm×d和U∈Rm×d分别是相关的负载向量矩阵，E和F分别是X和Y的残差。T和U的内部关系则由公式(9)表示

U=TB+R

(9)

其中B∈Rd×d是通过最小化残差R其中包含回归权值的对角矩阵。{TUPQB}是{XY}经过偏最小二乘法处理后获得的参数，即

(10)

而回归系数由式(11)表示：

CPLS=(XTX)++XTY=W*BQT

(11)

其中

(12)

(13)

0+是右逆，Im表示m行的单位阵，wi是PLS的权向量，Q是PLS的负载向量，p是Q的列向量，h表示PLS提取出来的主元个数，而CPLS是PLS算法的回归系数。当新数据到来时，偏最小二乘模型据式(14)进行更新。

(14)

其中，xnew是新的数据输入点，ynew是新的数据输出点。XNEW和YNEW则分别表示输入X的负载向量矩阵和输出Y的负载向量矩阵在新数据更新后的新矩阵。由上式可以看出，随着新数据不断的到来，矩阵的维数并没有发生变化，也因此大大加快了数据的处理速度和加快模型的处理速度。

2 自确认软测量方法

2.1 基于PCA的辅助变量传感器故障诊断与数据重构

不同于传统的基于PCA模型的SPE或T2的故障诊断方法，本文结合了SPE因子和SVI因子，并将它们用于故障的诊断。此外，利用方差分析方法URV(unreconstructed variance)在PCA模型建立之初对数据进行了主元个数进行合理的分析。具体如图1所示。

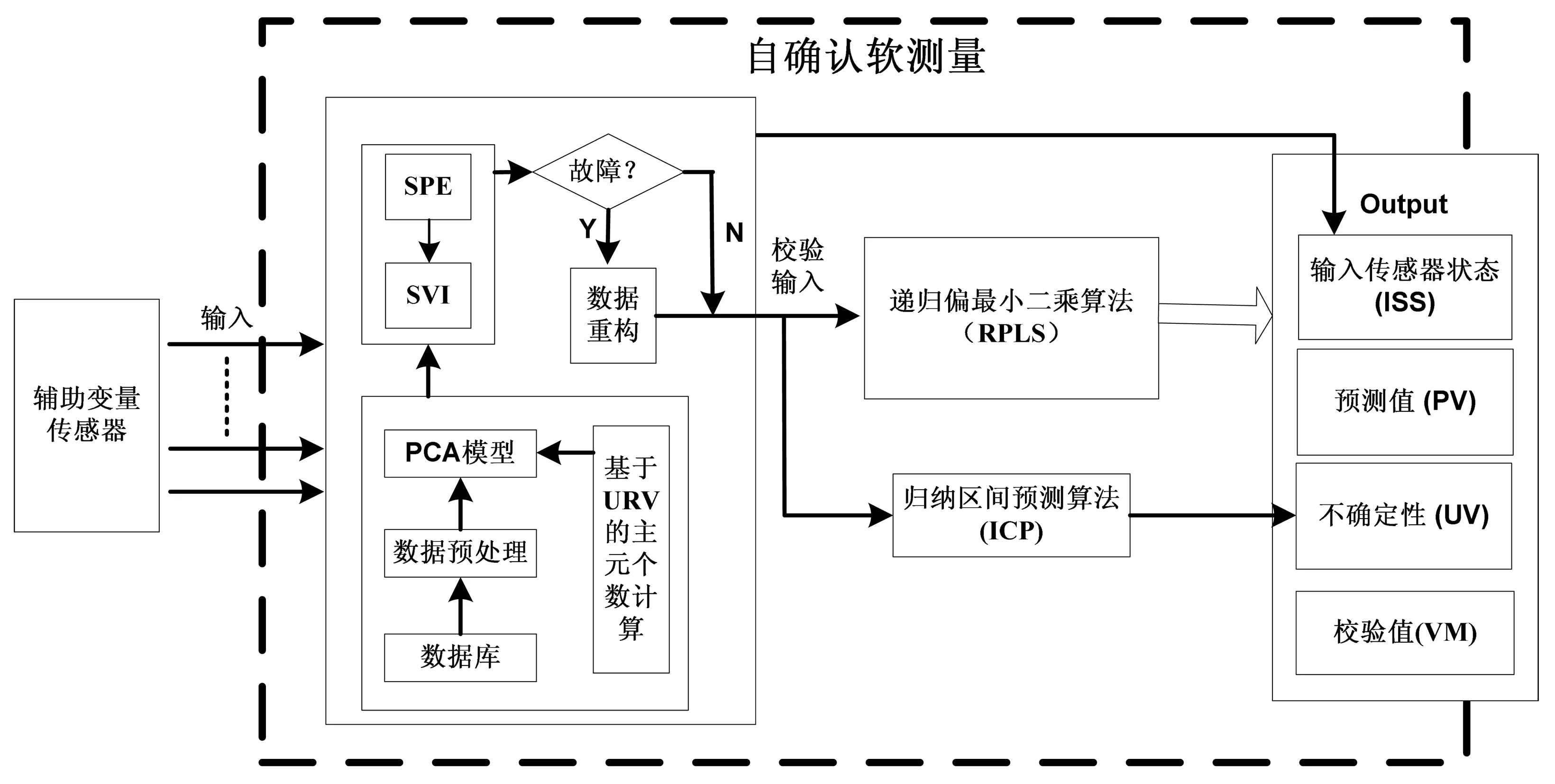
图1 自确认软测量框架Fig.1 Schematic of self-validating a soft sensor

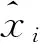
(15)

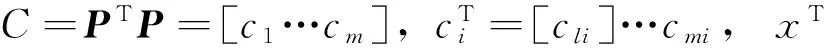
(16)

实际上，PCA模型主元个数的确定是相对主观的。如果故障传感器输入数据通过大量主元重构所得，则重构输入数据极大可能会包含大量主元所带来的噪声。相反，如果所确定的主元过少，所建立模型可能会由于故障数据得不到充分的重构而产生病态。此外，在PCA用于数据重构的过程中，主元的个数会进一步影响传感器的校验，如检测小故障的能力，故障辨识的自由度和重构的精确度。

Dunia等[13]发现当PCA模型用于重构故障传感器时，方差分析方法URV是可以在分析方差的同时，计算最优的主元个数，并且对重构效果有一定的指示作用。例如，变量i的重构方差ui表示，即xi-zi的方差计算如下：

(17)

2.1.2 故障检测和辨识 因为多传感器同时发生故障的可能性比较小，因此，此方法很容易能推广到多个不同时发生故障传感器的故障诊断。当某个传感器发生故障的时候，采样向量x可以表示为

x=x*+fεi

(18)

其中x*代表正常数据的部分,εi是故障传感器的单位向量，而f是故障的大小，可以为正值也可以为负值。为了说明方法的效果，重构数据表示为：

(19)

被重构的向量能被映射到模型和残差空间，从而计算出SPE如下：

(20)

如果第i个传感器发生故障同时j≠i，SPE(xj)不会发生明显变化。然而，如果选到真正的故障传感器，即i=j，SPE(xj)则会明显减小。同时，故障SPE(x)会急剧的变大，因此，本文设计的SVI因子如下：

(21)

其中1≤η≤0。从以上式子中可以看出，当发生故障时，SPE(xj)急剧减小，而SPE (x)会急剧的变大，因此SVI会近乎接近于0，即ηj近乎于0，同时比单纯的SPE(x)更加敏感。Dunia等[13]在他的文中给出了具体的讨论。此外，基于输入传感器彼此间的相关性，其它正常的相关传感器将被用来重构故障变量，从而使得软测量的预测更加稳定。

2.2 自确认软测量的多维度输出

从传统角度来说，软测量一般仅仅是作为未知信号的发生器。区别于传统的软测量，本文的自确认软测量不仅如上述描述的能输入传感器数据进行自校验，同时能产生多种信号：PV，ISS，OSS，VM和VU。

2.2.1 预测值(PV) 预测值与传统传感器的输出并无差异，即给定易测量传感器的输入在模型的基础上预测输出值。

2.2.2 输入传感器的状态(ISS) 输入传感器的状态表示了输入传感器在系统的运行当中所呈现的故障或正常运行状态。状态类别如表1所示。ISS能为现场操作人员提供现场仪表运行的直接决策依据。

表1 输入传感器的状态值Table 1 Input sensor status values

2.2.3 输出传感器状态(OSS) 由于污水厂现场条件的恶劣，在线仪表很容易偏离正常状态。另外，由于软测量模型独立于在线仪表，因此，本文提出了PV值，其可对在线分析仪表进行在线校验。和表1类似，共有5种状态对在线分析仪表进行故障显示。

2.2.4 不确定性校验 不确定，即UV值，能为真实的预测值提供可靠的置信空间，可以用于衡量模型和过程的噪声以及故障的影响。为了便于置信区间的描述，同时也是基于ICP(Inductive Confidence Predictor)算法的高效性，本文中利用ICP算法对软测量模型的不确定性进行了阐述。ICP算法，是主动的(Inductive)不确定性描述算法，较之于被动算法(Transductive)有更高的计算效率，具体可参见文献[14]。对于ICP算法，给定l个采样点的集合{(x1,y1),…,(x1,y1),(xl+g,yl+g)},其中i=1, …,l, 和一个新的输入点xl+g∈Rm。ICP假定输入点xl+g的可能输出值是yl+g，检验其拓展样本集合是独立同分布的，集合如下：

{(x1,y1),…,(xl,yl),(xl+g,yl+g)}

(22)

p(yl+g)=p((x1,y1),…,(xl,yl),(x1g,yl+g))=

(23)

其中# A代表了集合A中元素个数。假定可以计算校验集合中每个可能输出的p值，所有输出的p值在置信度以内则其至少有概率发生故障。因此，给定置信度1-δ，ICP算法的输出为：

{yl+g:p(yl+g)≻δ}

(24)

公式在文献[13]中得到了有效的证明。

为了使ICP算法和RPLS算法能够有效的结合，一致性测量指标是必不可少的。因为一致性测量指标是用来衡量真实输出值和预测值相对于采样点的重要指标，因此，其被定义为真实值和预测值的绝对误差：

(25)

ICP算法所产生的置信区间可为RPLS算法提供有效的置信空间。如果在线分析仪输出超出置信区间，现场操作人员需要多次确认从而确保仪表的可靠性。因此，RPLS软测量模型输出提供的不再是单调的预测值输出，而是包含了输出的校验的输出值。在软测量模型建模的过程中，数据选择算法选出来的数据被放入数据空间S中，无论是RPLS算法或ICP算法每次建模都是以这个数据空间的数据为基础的。具体RPLS算法和ICP算法的计算如表2所示。

表2 RPLS算法和ICP算法的结合Table 2 RPLS algorithm coupled with ICP Algorithm

2.2.5 校验测量值 鉴于现场复杂和恶劣的条件，在线分析仪表有极大的可能发生极端的或故障的情况。同时，即使仪表工作正常，仪表定期检测也是不可避免的。因此，有必要为仪表提供定时在线测量。在本文的软测量的建模过程中，在线分析仪表的输出和模型的更新是独立的。同时，由于软测量模型输出带有不确定上下限检验，因此，当其在线分析仪表发生故障时，能为其提供可替代的信息。

3 仿真实验

污水处理是一个复杂的生化处理过程，特别是污水厂的输入流量随着晴天雨天发生剧烈的变化，同时，其生物种群更是实时的发生变化，且工艺知识也不尽完善，加之现场条件恶劣，仪表发生故障的概率也随之增加。BOD5是测量有机物重要的出水指标，也是重要的检测参数。目前BOD5的测量无法进行实时在线检测，而市场上现有的实时在线5 d BOD 测量仪表造价很高，实用性和通用性差。因此，实现BOD5的实时在线测量显得至关重要。校验数据来源于巴塞罗那的一个污水厂，将近2年400组数据。每组数据有38个变量。本文中利用Kohomen的自组织神经网络 (SOM)检测和选择相关向量[15]，因此，经过选择辅助变量如表3所示。其中200组数据用来训练模型，另外200组数据用来校验模型，而输出是BOD5，输入变量是19个辅助变量。

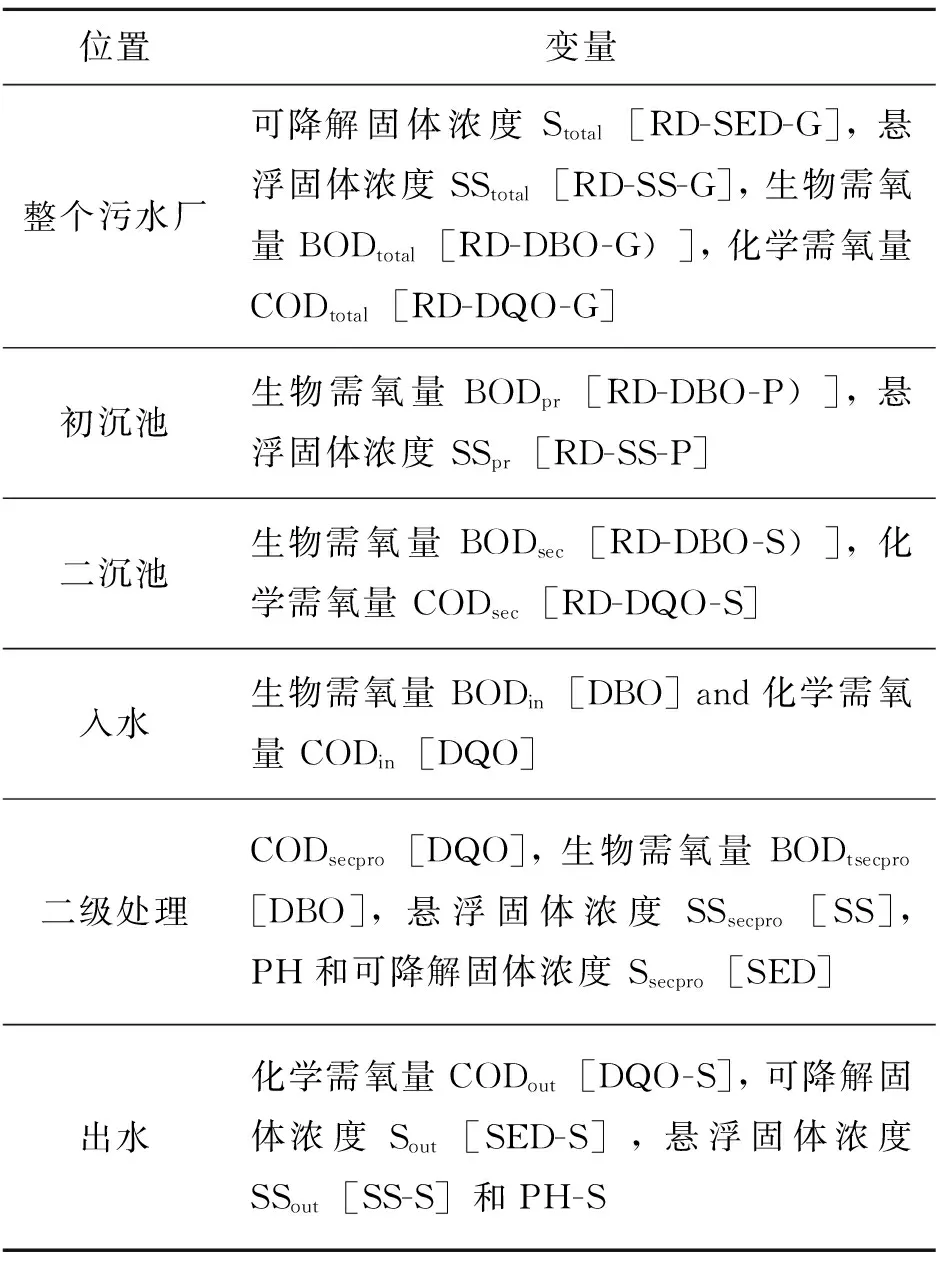
表3 辅助变量表Table 3 Auxiliary variables

3.1 自确认软测量的输入传感器的校验

为了得到最佳的主元个数，通过相关性进行彼此检测URV的计算，URV达到了最小值，PC为9时被用来作为PCA模型的主元个数。传感器仪表都处于正常状况下，200组数据被用来训练PCA模型，而其他200组数据用来校验PCA模型，从而得到了PCA模型和正常状态的阈值。为了确认PCA模型对软测量的校验作用，我们假定二沉池的pH值发生阶跃性的传感器故障，如图2(a)所示从第120天到170天有8左右的偏差。而从图2(b)中可以看出SPE和SVI能很轻易的检测出传感器的故障，SPE值明显超出了控制限，经过数据重构以后，SPE能很快的回复正常，但是仍然发生误报警现象，如图2(d)而SVI比较稳定，很快定位出了是pH传感器发生故障，其SVI值几乎接近于0(其他传感器的SVI值则都近乎于1，图中没显示)，并且没有误报警现象。同时，传感器在数据重构以后，很快的转入了正常状态。另外，图2(a)显示了重构值和实际值能够很好的吻合，说明了重构的精确性。同时，SEVA软测量不仅能辨识和重构故障，而且能进一步显示输入传感器的状态，正如图2(c)所示，如果二沉池的pH值发生8左右的偏差从第120天到170天，由于故障的发生，ISS CLEAR 状态转变到了BLURRED状态，同时没有显示是不是永久性故障。但是由于PCA模型对故障的检测和重构，pH传感器跳到了DAZZLED状态，并保持这个状态直到仪表恢复，并使得ISS在第170后跳到了CLEAR状态。

3.2 自确认软测量的预测模型的校验和不确定值(UV)的输出

为了显示预测模型的预测误差，文中引入的均方差(RMSE)和相关系数是准确的评估软测量模型的重要指标。因为污水厂的复杂性，不仅受到季节变化、晴雨变化以及污水中微生物变化的影响，单纯的预测值输出的软测量模型不能很好的确定其模型以及外部的不确定性，因此，我们利用ICP算法来计量预测输出值的置信区间，从而来描述模型的不确定性。从图3显示，由于在过渡过程中过程变量偏离原本的稳定状态，UV会相对应的放大以及对相应的不确定性作出指示。

3.3 校验值(VM)，输出传感器状态(OSS)以及其故障诊断的应用

在工业现场中，在仪表校验或运行的时候，遭遇噪声的概率极高，因此，对软测量输出或在线仪表的输出的校验是必不可少的。由于RPLS软测量模型的输出是独立于在线仪表输出的，因此，软测量的输出及其置信区间能用来校验在线仪表。正如图4(a)和(b)分别分析仪表发生突变和输出值漂移两种故障，在90%的置信度下，都能够准确的检测出来。此外，SEVA软测量能够很好的校验软测量在线仪表能否发生故障并且指示出在线仪表当前的状态，从而进一步确认UV的有效性和其应用于获取VM(此处即软测量的输出值)。

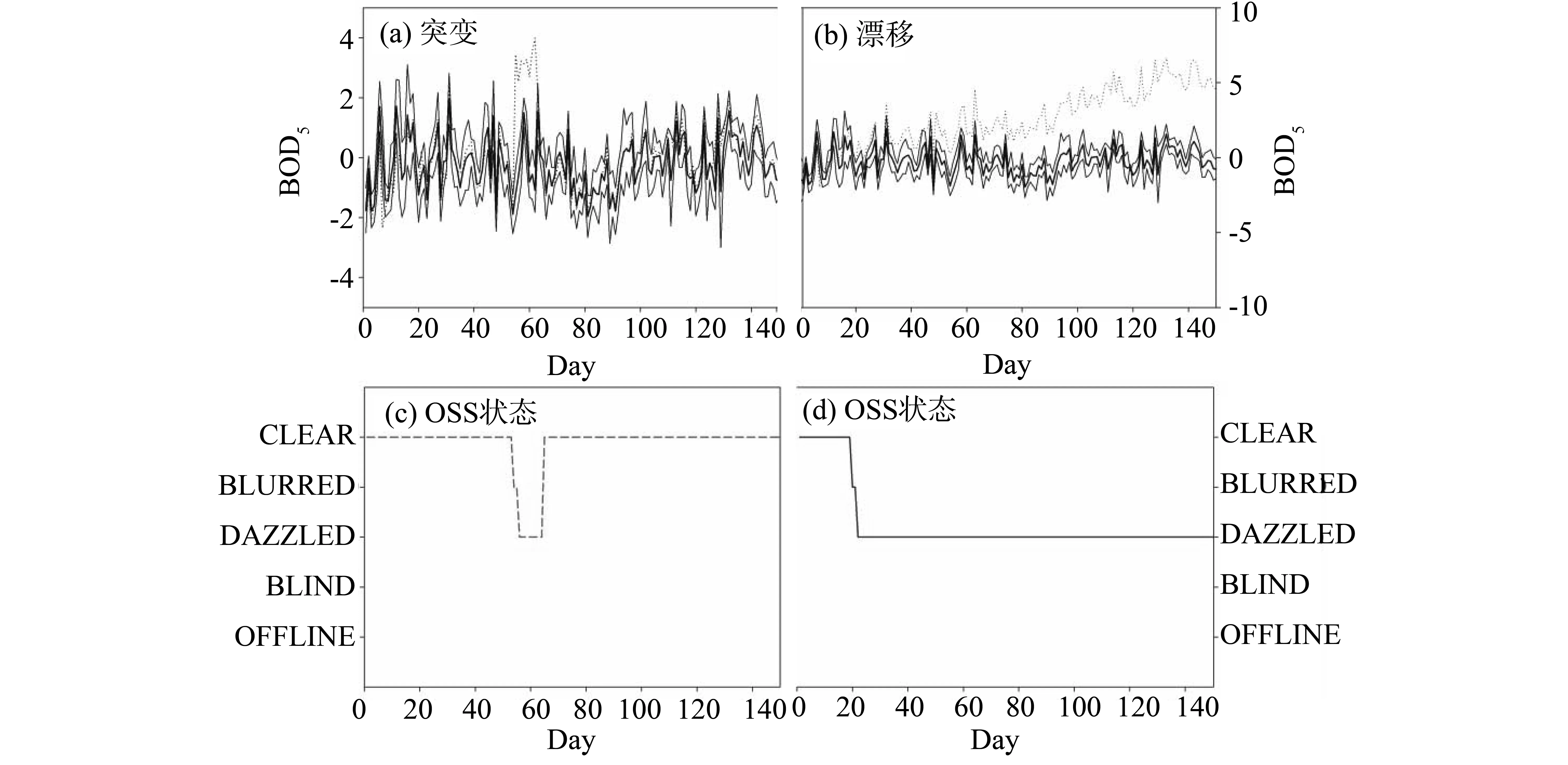
图4 突变和漂移两种故障状态下的故障诊断以及状态预警Fig.4 Fault detection, diagnosis and status alarm under the bias and drift scenario

4 结 论

本文解决了传统软测量的不可靠性问题，并提出了SEVA软测量模型的概念。SEVA软测量不仅能实现模型的自诊断和数据的自重构，而且能够提供多种输出，包括预测值(PV)，软测量输入传感器状态(ISS)，输出传感器状态(OSS)，校验输出(VM)和能描述软测量输出可信度的不确定性值(UV)。算法在污水厂的BOD5预测中得到了广泛的应用。基于PCA模型的SPE和SVI指标能很好的辨识和重构软测量某个输入传感器发生故障时候的数据，而且RPLS算法能在出现故障的情况下预测污水厂的出水指标。此外，SEVA软测量还能用于校验在线仪表，这些在污水厂的出水指标预测中得到了进一步的验证。所提出方法能推广到其他类似的大延迟生化处理过程。

[1] 黄道平,刘乙奇,李艳.软测量在污水处理过程中的研究与应用[J].化工学报,2012,62(1):1-9.

[2] 李战明,王云峰, 袁占亭.基于流量特性的调节阀阀芯曲线智能拟合[J].中山大学学报：自然科学版,2009,48(1):22-25.

[3] 汤仪平,金福江.低浓度混合染料间歇式染色过程色泽软测量[J].仪器仪表学报,2011,32(3):690-694.

[4] YAN W, SHAO H, Wang X. Soft sensing modeling based on support vector machine and Bayesian model selection [J]. Computers & Chemical Engineering, 2004, 28(8): 1489- 1498.

[5] KADLEC P, GABRYS B, STRANDT S. Data-driven Soft Sensors in the process industry [J]. Computers and Chemical Engineering, 2009, 33(1): 795-814.

[6] YUE H H, QIN S J. Reconstruction-Based Fault Identi-fication Using a Combined Index [J]. Industrial & Engi-neering Chemistry Research,2001, 40(20): 4403-4414.

[7] MARTIN E B, MORRIS A J. Non-parametric confidence bounds for process performance monitoring charts [J]. Journal of Process Control, 1996, 6(6): 349-358.

[8] 罗中良, 麦宜佳, 余剑峰. 基于多传感器的神经网络模式识别方法 [J]. 中山大学学报：自然科学版,2001,40(5):21-24.

[9] QIN S J, YUE H, DUNIA R. Self-Validating Inferential Sensors with Application to Air Emission Monitoring [J]. Industrial & Engineering Chemistry Research, 1997, 36(5): 1675-1685.

[10] HENRY M P, CLARKE D W. The self-validating sensor: rationale, definitions and examples [J]. Control Enginee-ring Practice, 1993, 1(4): 585-610.

[11] LIU X, KRUGER U, LITTLER T, et al. Moving window kernel PCA for adaptive monitoring of nonlinear processes [J]. Chemometrics and Intelligent Laboratory Systems, 2009, 96(2): 132-143.

[12] JOE Q S. Recursive PLS algorithms for adaptive data modeling[J].Computers & Chemical Engineering, 1998. 22(4/5): 503-514.

[13] DUNIA R, QIN S J, EDGAR T F, et al. Identification of faulty sensors using principal component analysis [J]. Aiche Journal, 1996, 42(10): 2797-2812.

[14] PAPADOPOULOS H, PROEDROU K, VOVK V, et al. Inductive confidence mach-ines for regression [C]∥ECML 2002 in Machine Learning ,Berlin: Springer, 2002:185-194.

[15] RALLO R, GIRALT F. Best feature selection and data completion for the design of soft neural sensors [C]∥ Proceedings of AIChE 2003, 2nd Topical Conference on Sensors ,San Francisco: ACS, 2003.