基于自学习多维参数可信安全度量模型研究*
蔡庆玲, 詹宜巨,杨 健
(1.中山大学工学院, 广东 广州 510275;2. 广东工业大学自动化学院, 广东 广州 510006)
可信计算是目前信息安全领域的研究热点[1-2]。可信度量是可信计算的关键技术之一[3-4]。而目前可信度量的方法主要采用单一的软件完整性检验。其存在缺陷主要有[2,4-6]:软件完整性检验的计算量过大问题;难以有效解决动态环境下完整性检验的实时更新问题;难以实施动态环境下完整性检验计算端与验证端的同步问题;对资源受限的设备如移动终端细粒度完整性检验实现的策略问题。
为此,本文依据软件安全保护原则提出一种综合的可信度量的建模方案——随机抽取划分序列策略模型(Random Division Sequence Model,DR)[7]。
1 可信度量模型相关问题研究
1.1 可信度量模型问题分析
可信计算环境的建立依靠着可信根、可信链的建立和传递,可信链的建立和传递又离不开可信计算的关键技术——可信度量。目前可信度量的方法主要采用单一的软件完整性检验,即将整个软件进行哈希摘要形成参考完整性值作为该软件完整性检测的安全依据。
可信计算环境又可分为静态可信计算环境和动态可信计算环境。其中静态可信计算环境中,采用单一的软件完整性检验还可以勉强胜任,但在动态可信计算环境下,随着用户开启的应用程序不同,系统完整性是动态变化的。因而,必须实时地更新系统的完整性信息,如操作系统内核、用户动态进程,还要兼顾着各进程的运行参数、堆栈区及数据区域的完整性检验。实时的、全面彻底的动态完整性计算,虽然提高了计算平台安全可信的可能性,但必然会导致系统整体性能的下降,这对资源有限的设备问题就尤为突出。另一方面更因为动态环境下安全性已不仅仅依赖于执行单一软件的完整性检验,其情况极为复杂多变,如计算平台常驻内存代码(如操作系统中的系统调用、服务器进程等)仅在加载文件时进行完整性度量,必然会造成完整性度量的盲区,遗留安全隐患。此外还有程序的运行参数、堆栈区及数据区域的不断地更新等都无法作到完整性检验的实时、全面彻底不留有漏洞。
由此可见,一方面,软件完整性检验的计算量大,尤其是动态环境下完整性的复杂多变,其目标完整性值需要实时更新,对资源受限的计算设备难以胜任。另一方面,传统单一软件完整性检测方案,难以解决动态环境中完整性检验计算端与验证端的同步实施问题。需要一种兼顾多方面安全需求低耗高效的、综合性的可信度量策略及构造方法,才能解决动态环境中完整性检验有效实施的多项难题。
1.2 软件安全原则及保护机制
目前,信息安全领域被广泛认可的原则主要有[7]:等级保护原则、适度安全原则、动态安全原则及全过程安全原则。
等级保护原则: 对信息系统的安全特性进行等级划分,应按标准进行建设、管理和监督。
适度安全原则: 信息系统安全措施的强度与该系统承担的业务职能和系统的重要性紧密相关。采用适度安全原则,有效的控制浪费和不足。
动态安全原则: 网络环境的动态变化,攻击手段的更新,安全解决方案也需随之变化。安全框架应随威胁和网络环境的变化而不断调整。
全过程安全原则: 当安全防护在任何一个环节出现漏洞,风险都将会在此点发生,并渗透到其它环节。故应采用全过程安全原则对风险实施安全监控。
2 多维参数可信度量模型设计

设计思想:
计算端将软件按照摘要划分单元长度l(本文哈希函数使用MD5,l选为512bits)进行划分,对每一个划分进行哈希摘要,计算端和验证端共同保存作为验证RIMi值序列(见图2)。可信度计算验证时,验证端按照模型DR抽取相应的若干划分进行摘要计算和验证。

图1 随机数R为1的位表示将被抽取的划分序列
Fig.1 1 bit of random number R indicates that the sequence will be extracted
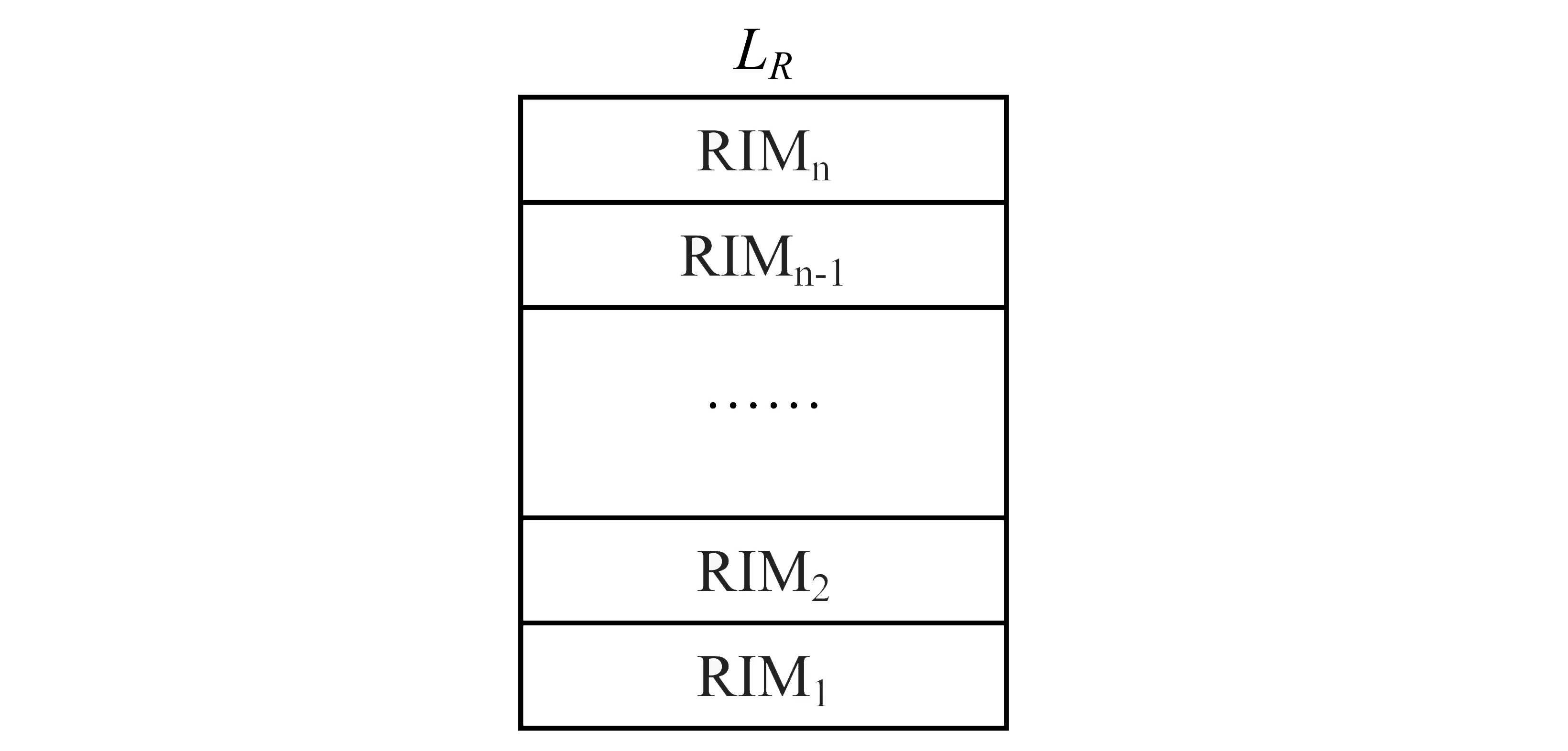
图2 软件P的基本划分序列LRFig.2 The basic division sequence LR for the software P
软件P模型:
软件P模型表示为:元组P(L,Kr,Ke,Kc,LR),其中LR=(RIM1, RIM2, …, RIMn)
L:为待检测的软件长度;
Kr:为该软件安全度需求系数;
Ke:为该软件安全度评估系数;
Kc:为执行该软件所需资源开销系数;
RIMi:为划分i的完整性验证参考值。其中RIMn长度 随机抽取划分序列策略模型: 随机抽取划分序列策略模型表示为:元组DR(R,Kr,Ke,Kc,LD), 其中LD=(L1, …,Li, …,Ln-1,Ln) R:高熵随机数,用于确定摘要所抽取的划分(见图1); l:摘要划分基本单元长度; Kr=N时,表明该软件每一个划分都必须进行完整性检验; Kr=0时,表明该软件都不需要进行完整性检验。 Ke:软件安全度评估系数,依据该软件执行的评估结果动态调整,0≤Ke≤N。 Ke=N时,表明该软件每一个划分都具有可信安全性; Ke=0时,表明该软件每一个划分都不具有可信安全性。 Kc:执行该软件所需资源开销系数,软件执行时间及所需资源越多则Kc越大,取值为:0 Kc=10时,表明该软件执行时间及所需资源等级为最高; Ke=0时,表明该软件执行时间及所需资源等级为最低。 抽取的划分序列LD表示为:(L1, …,Li, …,Ln-1,Ln) Li=1时,则表明序列号为i的划分块被抽取,参与完整性检验; Li=0时,则表明序列号为i的划分块未被抽取,不参与完整性检验。 |LD|:为序列中元素为非0的个数; 随机抽取划分序列执行过程: 模型DR(R,Kr,Ke,Kc,LD)用于生成抽取划分序列LD,其中R为一高熵随机数,其格式见图1。用于随机地确定初时抽取的划分块。Kr,Ke,Kc共同对R值的进行修正。因此LD是由R,Kr,Ke,Kc四个参数共同决定,最终确定的完整性检验所抽取的划分。具体执行算法如下: 1) 随机选取高熵随机数R,R为1的位表示将被抽取的划分序列号。 2)Kr为该软件安全度需求系数。在系统运行中,Kr值保持不变。Kr越大表示该软件安全要求越高。初始时由系统根据软件的安全度需求进行赋值,其取值为 0≤Kr≤N,如操作系统等为最高安全度需求Kr=N。Kr用以调整R取值,表示为:∑Kr·R。依据等级保护原则,Kr取值越大,则R取1的位越多,表明抽取划分的越多;Kr取值越小,则R取1的位越少,表明抽取划分的越少。 因此模型DR参数之间的关系可表达为 5)当|LD|>|LR|, 需要抽取的更多划分,执行如下程序: (a)如果 |LD|>|R|, 再生成随机数R′; (b)计算:R=RorR′; (d)判断是否满足:|LD|≤|R|; (e)如果不满足,则重复操作(a)-(d); (f)如果满足,则按照LD序列抽取相应的划分。 随机抽取划分序列策略模型性能分析: 系统运行后,其中Kr,Ke,Kc参数通过自学习、自适应不断调整最终得到优化,并趋于稳定。 本文提出的随机抽取划分序列策略模型DR融合了多方位参数,摒弃传统单一度量方案,建立了综合性的可信度量策略及构造方法,兼顾了多方面安全需求问题,实现了细粒度完整性检验,为可信度量的建模提出了新的思路。 [1] 2012年度国家有关“可信软件基础研究”重大研究计划科技项目指南[R]. http:∥www.ecas.cn/xxkw/kbcd/201115_85123/ml/xxhjsyjcss/201202/t20120216_3441065.html. [2] 刘昌平. 可信计算环境安全技术研究[D]. 成都:电子科技大学, 2011. [3] 蔡红云, 田俊峰, 李珍. 何莉辉基于信任领域和评价可信度量的信任模型研究[J]. 计算机研究与发展, 2011, 48(11): 2131-2138. [4] 王丹, 卢彦, 赵文兵,等.基于变量间依赖关系的软件可信度量模型[J]. 华中科技大学学报: 自然科学版, 2013, 41(1): 41-45. [5] 杨蓓, 吴振强, 符湘萍. 基于可信计算的动态完整性度量模型[J]. 计算机工程, 2012, 38(2): 78-81 [6] 刘孜文, 冯登国. 基于可信计算的动态完整性度量架构[J]. 电子与信息学报, 2010, 32(4): 875-879. [7] 计算机信息系统安全保护等级划分准则GB17859-1999[S]. http:∥www.docin.com/p-396913971.html.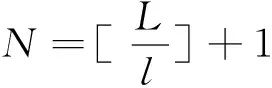
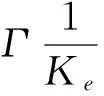
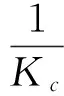
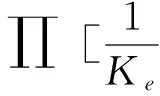
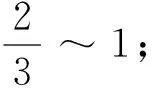

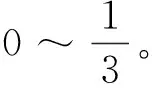
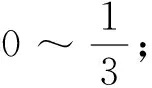
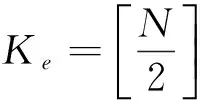
3 结 论

