基于多目标和声搜索算法的城市单向交通组织优化研究
董洁霜, 王伟智, 刘魏巍
(1.上海理工大学管理学院,上海 200093)
在绿色高效的出行要求下,快速高效的城市路网设计成为当下的研究热点,但是,在有限的经济条件下,不可能同时进行大规模的交通基础设施建设[1],因此,交通部门往往倾向于对现有的道路网进行优化,期望投入较小的成本,实现交通设施的高效运行.
2006年Giridhar等将启发式算法应用到道路和信号灯设计方面[2].2008年Pinninghoff等用进化算法解决洛杉矶城市道路网优化问题[3].2010年Sanchez-Medina等采用遗传算法解决西班牙某城市交通信号优化问题[4].2011年Mesbah等应用进化算法求解交通控制优先模型[5].2011年Sohn应用标优化技术,在对城市交通的影响度最小的前提下,解决了机动车与非机动车交通空间分配问题[6].
2009年史峰等将城市道路分为干道(较宽、双向通行)、支路(较窄、单向通行),在减少污染、缓解拥堵的前提下,解决了城市单向交通组织优化问题[7].2010年龙东方等为了避免支路超负荷,用模拟退火算法代替遗传算法[8].
本文阐述一种新的智能算法,用以处理单向交通重组优化问题(ROWTOP),运用多目标和声搜索算法解决复杂的单向交通重组优化问题,并在案例中与一般算法进行比较分析.
1 目标函数
对于城市主要道路交通受到严重影响的区域,单行道组织优化是一种高效的应对措施.使用有向图G(v,ε,s)表示路网,v代表节点集,ε表示道路集,s(s∈S)表示方向集,S表示道路的可通行方向.本文中道路分为主干路和单行路,因此,|S|=3,方向集是由单行路方向子集s0、主干路方向子集st组成.
有向图中A,B表示进入点和离去点,A,B∈v,单向交通重组优化问题得到最优的单行路方向集s0,使得A→B的出行时间最短,本文中最短出行时间将采用A→B路径中的途经点数量表示.
单向交通重组优化问题的本质是寻找单行道的最优方向子集s0*,目标函数为
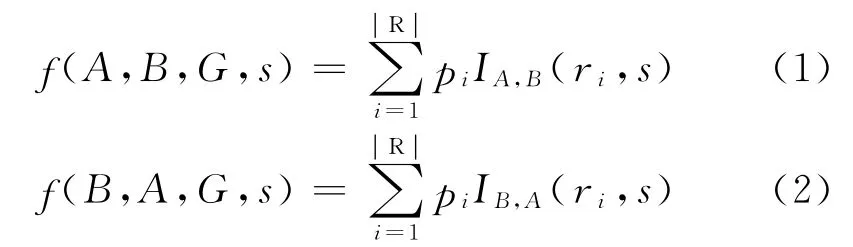
式中,IA,B(ri,s)表示车辆沿路径ri由进入点A到离去点B所途经的节点数量,ri∈R;pi表示车辆选择路径ri的概率.
为了避免死循环,需要设定车辆到达离去点之前途经点的最大值,并定义路径A→B(或B→A)单辆机动车的最小跃点数(一辆机动车在该路径通行的途径路段数),使用Dijkstra算法进行求解.假定s=st(如所有的街道都是双向的,s0=∅),可以计算跃点数的下限值(A,B,G),显然,
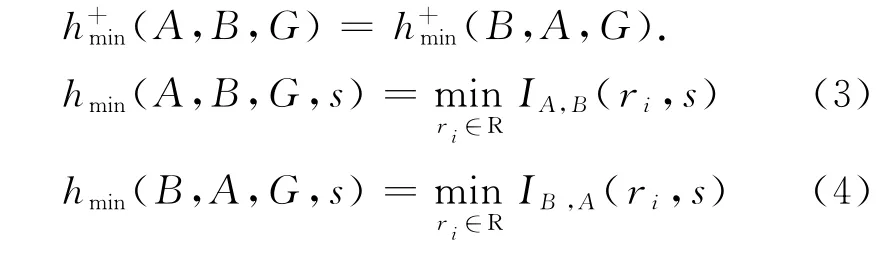

1.1 目标函数计算
G+表示由5个节点和5条边组成的有向图,如图1所示,由进入点A=1至离去点B=5,跃点数下限值h+min(1,5,G+,s)=2.

图1 f(·)计算图Fig.1 Calculation of objective function f(·)
观察图1,可以暂定点4、点5是离去点,一辆车将由A出发,可能在点5离开路网,也可能在点4离开路网.第一种情况下,最短路径由点1出发途经点3直接到点5,概率为p0=p12p35(pij为从i→j的概率),在同样情况下,经过k次循环1→3→2→1后到达点5离开,其概率为
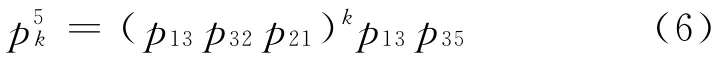
在不计损失的情况下,某点到其相邻点的概率是相同的,p13=1,p32=1/2,p21=1.
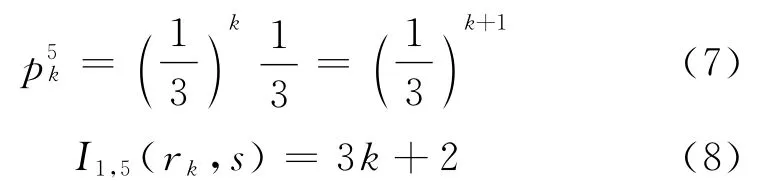
式中,rk表示从图1中点A=1经过k次循环到点B=5.
设途经点数量上限L=15,因此,I1,5(rk,s)=3k+2≤15,k≤13/3,取k=4,得
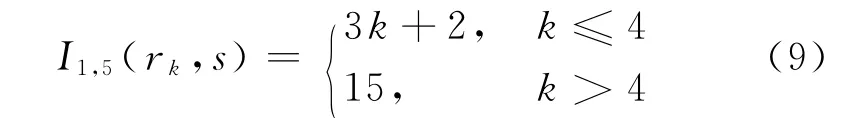
第二种情况是车辆经过k次1→3→2循环后到达离去点4,每条路径的概率为

由上可得,到达离去点B=4的概率为
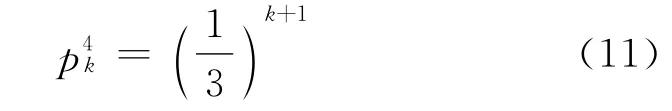


1.2 目标函数近似计算
为了降低计算的复杂程度,使用蒙特卡罗模拟方法估算函数值,N辆机动车从点A出发选择路径ri到达点B,而pi等于车辆数目Ni与N(N→∞)的比值,即

式中,N代表从点A出发到达点B的所有机动车数量;Ni代表从点A出发选择路径ri到达点B的机动车数量.
式(1)可以改写为


图2 不同机动车数量下的f+min(1,5,G+,s)估计值变化图Fig.2 Example of objective function estimation f+min(1,5,G+,s)using different number of vehicles N
2 多目标和声搜索算法
应用合理的多目标搜索方法能够生成双目标函数的平衡解,本文中选取新的多目标计算方法——和声搜索算法(Harmony Search)[9-11],简称HS算法.
算法可以概括为以下4个步骤:
a.初始化,过程只在第一次迭代中进行.首先生成和声记忆库双向道路的值为2,其它单行路值从{0,1}中随机选取,为避免断路,要求每一个节点至少有一条出路.
b.创作,对si(k)≠2的音调采取3种不同的概率方式产生新解集,生成新的解集(K集),概率分别为和声记忆搜寻率(HMCR)、记忆调整率(PAR)、随机选择率(RSR).
c.在寻求合适的f(A,B,G,s)与f(B,A,G,s)目标下,每次迭代都会产生优于之前的结果,最重要的是和声记忆中储存的是非支配排序解,同时有助于Pareto最优收敛.首先,音调顺序与其非支配水平相关联(1最好,2次之,等);然后,群聚距离表示与每个目标值最邻近的间距之和,依据群聚距离定义每个元素的顺序,为了覆盖目标总体空间,每个解间必须有一定的间距;最终,和声记忆库中储存经过筛选的最优K集[12].
d.当达到最大迭代次数T时计算停止,第一非支配水平的解集表示Pareto前沿近似结果;如果未达到迭代次数T,则会返回步骤b继续计算新的K集.
3 案例应用
为了评估多目标和声搜索算法的性能,在一定数量不同规模的ROWTOP算例和实际案例中进行验证性对比分析.
3.1 蒙特卡罗算法比较
为了评估HS算法性能,与蒙特卡罗算法进行对比,蒙特卡罗算法是智能交通优化中较为常用的一种算法.蒙特卡罗算法步骤如下:
a.首先清空图G中的单向边的方向,假设每条边可以是任意唯一方向.
b.计算式(3),应用Dijkstra算法获得A→B途经节点数量的最小值.
c.根据步骤b的输出结果,构造属于A→B的最优路径的单向边方向集.
d.计算式(4),再次应用Dijkstra算法获取B→A的途经节点数量最少的路径,在步骤c中已确定方向的单向边在本步中不参与计算.
e.根据步骤d的输出结果,构造属于B→A的最优路径的单向边方向集.
f.从步骤b开始重复,直到不存在其它A→B(或B→A)的路径.
通过迭代计算得到单向边方向集,从而确定最优路径.在迭代过程中,包含单向边的最优路径在下一次的搜寻过程中将被剔除,因此,这是一种贪婪式的局部最优构建方法(GCA).虽然此方法比较简易,但仍是检验多目标和声算法性能的合理参考算法.GCA算法既不是随机的,也不是多目标的,然而,f(·)近似值、(A,B)或(B,A)方向集的最小跃点数可以用来作为评价标准.
3.2 算例检验
首先用随机生成的有向图{Gi(v,ε,s)}4i=1表示不同的ROWTOP算例,改变节点数量、边、进入点、离去点进行多次计算,构造网络节点图(SLG),系数α和β分别设为100和3能够满足实验需求,表1中给出了相关参数参考值.

表1 多目标HS算法相关参数建议值Tab.1 The suggested parameters utilized for multi-objective HS algorithm
表2和表3列出了SLG算例的结果,算法输出的是单向交通重组优化问题算例的Pareto前沿估计结果,得到的每个要素值f(A,B,G,s),f(B,A,G,s),hmin(A,B,G,s),hmin(B,A,G,s)是经过30次的算法独立运算的估计值,双向平衡策略简称为ROB,整体Pareto最优前沿估计值表示为ULT.
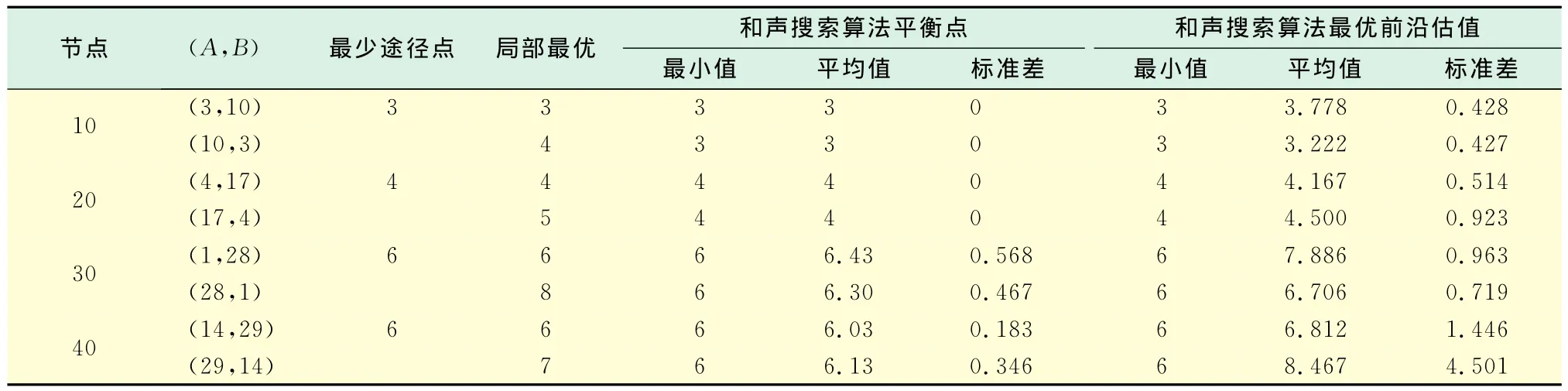
表2 GCA算法与HS算法关于hmin(·)结果对比表Tab.2 Satistics for hmin(·)obtained by GCA and HS heuristics
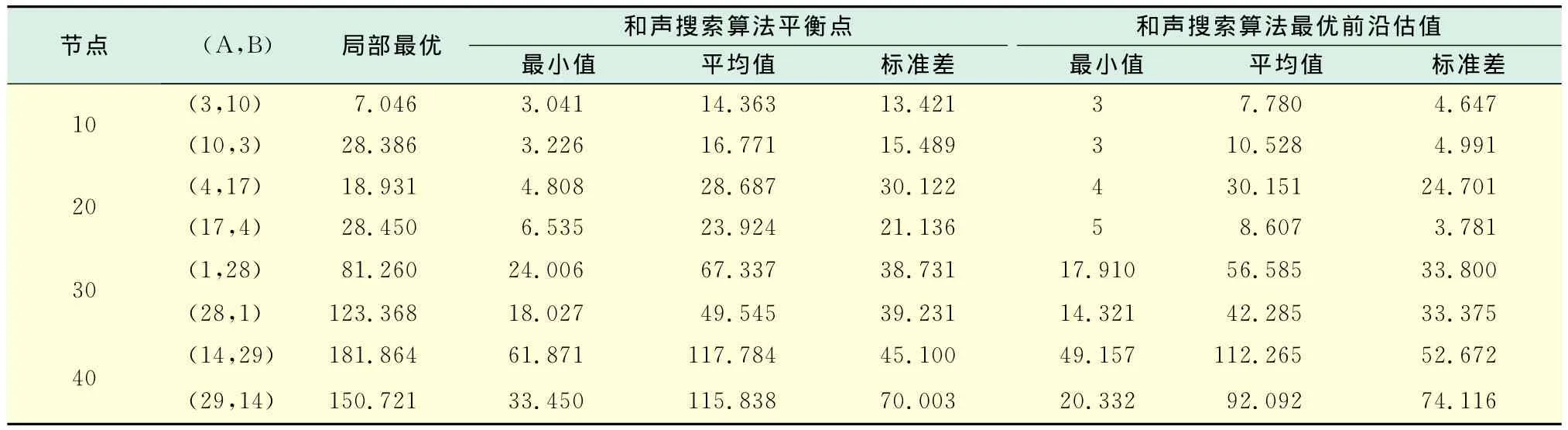
表3 GCA算法与HS算法关于f(·)结果对比表Tab.3 Statistics for f(·)obtained by GCA and HS heuristics
表2列出了GCA算法和HS算法的最少途经点hmin(·)统计结果,也包括h+min(·)(即在不进行单行限制的情况下(A,B)途经点的最小值).GCA算法寻找正向最短路径过程中途径点更接近于h+min(·)值,但是,对于逆向(B,A)的计算效果却很差.
表3中f(·)的统计结果能够体现算法的实际性能,因为,f(·)表示路网中加入交通流的复杂情况下的计算结果.HS方法得到的路线使得平均途经点数量尽可能少,虽然在算例中ROB和ULT统计的f(A,B,G,s)平均值可能会比GCA算法得到的f(A,B,G,s)要大,但f(B,A,G,s)的平均值却明显小于GCA算法得到的结果.
图3表示各算例应用HS算法得到的Pareto前沿近似结果和有向结构图.d为距离.

图3 优化结果及有向结构图Fig.3 Optimization result and graph for the solution
3.3 实例检验
为了验证算法的可行性,现选取某市区为研究范围,每天在早高峰时间,大量的商家在这里进行交易,道路资源的占用,导致了严重的交通矛盾.研究范围内单行支路比较丰富,但是,缺乏有效的单向交通组织策略,实际路网如图4所示(见下页).
在图4中用同心圆点表示城区街道的进入和离去端点,点划线圈内表示受影响严重的区域.图4中共有119个节点,|v|=119.节点1表示来自(到)市南区的进入点(离去点),节点35表示来自(到)市中心的离去点(进入点).图5(见下页)表示经过多目标和声算法得到的双向情况下的f(·)最佳平衡值,在该情形下,从点1到点35途经16条线段,从点35点1经过18条线段,将真实的情况用有向图来解释,通过式(5)得到的h+min(·)=17,揭示了HS算法在寻找最短路径的优异性能.
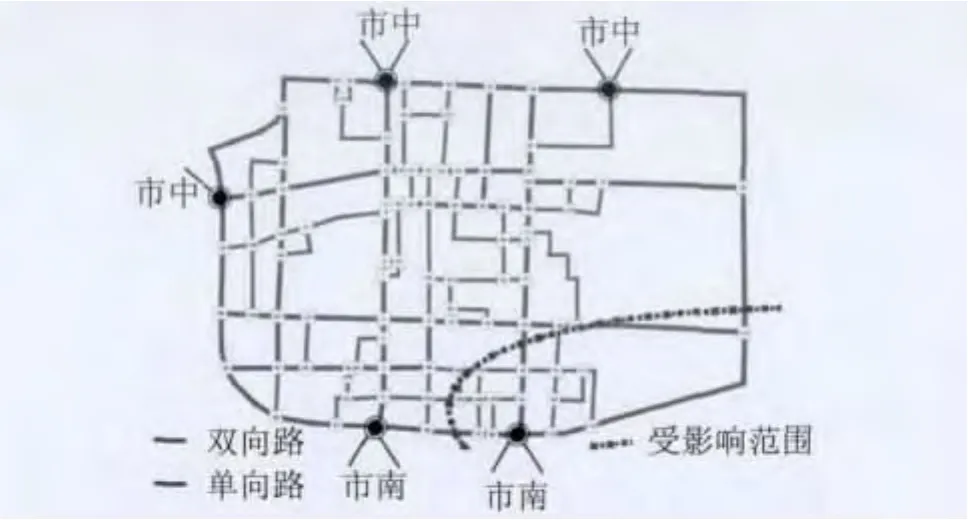
图4 实例路网以及影响范围Fig.4 Real network and space of influence

图5 单向交通组织规划图Fig.5 Programming diagram of one-way traffic organization
图6表示进行30次和声搜索算法后得到的Pareto前沿结果.从图6可以看出,产生了较宽包络面,足以说明其平衡性.
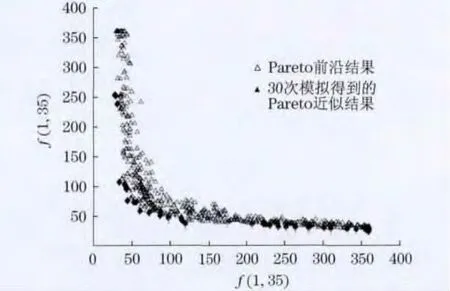
图6 关于ROWTOP实例的Pareto前沿近似结果Fig.6 Pareto front approximations of real instance obtained in ROWTOP
4 结 论
提出了一种多目标和声搜索的启发式算法(HS),用以解决城市交通矛盾突发时的单向交通组织问题,并对该问题进行了求解说明,包括2个目标函数以及如何用蒙特卡罗模拟方法求解.描述多目标和声搜索算法的计算步骤,并与一般算法相比,在不同的算例和实例中验证了HS算法的平衡性和高效性.通过计算模拟,证实该方法能够得到近于最优的单行道重组方案,以提高当城市交通冲突发生时路网2节点间的机动车通行性能,减轻部分区域道路阻断对整个地区的通勤影响.
[1] 董洁霜.港口集疏运系统优化模型[J].上海理工大学学报,2007,29(5):453-456.
[2] Giridhar A,Kumar P R.Scheduling automated traffic on a network of roads[J].IEEE Transactions on Vehicular Technology,2006,55(5):1467-1474.
[3] Pinninghoff M,Contreras R,Atkinson J.Using genetic algorithms to model road networks[J].IEEE Computer,2008,41(12):60-67.
[4] Sanchez-Medina J J,Galan-Moreno M J,Rubio-Royo E.Traffic signal optimization in“La Almozara”district in saragossa under congestionconditions,using genetic algorithms,traffic microsimulation,and cluster computing[J].IEEE Transactions on Intelligent Transportation Systems,2010,11(1):132-141.
[5] Mesbah M,Sarvi M,Currie G.Optimization of transit priority in the transportation network using agenetic algorithm[J].IEEE Transactions on Intelligent Transportation Systems,2011,12(3):908-919.
[6] Sohn K.Multi-objective optimization of a road diet network design[J].Transportation Research Part A,2011,45(6):499-511.
[7] 史峰,黄恩厚,陈群,等.城市微循环交通网络中单行交通组织优化[J].交通运输系统工程与信息,2009,9(4):30-35.
[8] 龙东方,史峰,王英姿.基于道路负荷与公平性的单向交通组织优化[J].交通运输系统工程与信息,2010,10(6):109-114.
[9] Landa-Torres I,Gil-Lopez S,Salcedo-Sanz S,et al.A novel grouping harmony search algorithm for the multiple-type access node location problem[J].Expert Systems with Applications,2011,39(5):5262-5270.
[10] Geem Z W,Kim J H,Loganathan G V.A new heuristic optimization algorithm:harmony search[J].Simulation,2001,76(2):60-68.
[11] 刘思远,柳景青.一种新的多目标改进和声搜索优化算法[J].计算机工程与应用,2010,46(34):27-30.
[12] Deb K,Pratap A,Agrawal S,et al.A fast and elitist multiobjective genetic:NSGA-II[J].IEEE Transactions on Evolutionary Computation,2002,6(2):182-197.

